【机器学习】04-回归与聚类算法:线性回归、过拟合、逻辑回归、K-means算法
回归与聚类算法
一、线性回归
学习目标:
- 记忆线性回归的原理过程
- 应用LinearRegression或SGDRegressor实现回归预测
- 记忆回归算法的评估标准及其公式
1)线性回归即解决回归问题的最基本一个算法。
回归问题:目标值为连续型数据的一类问题。
2)线性回归应用场景
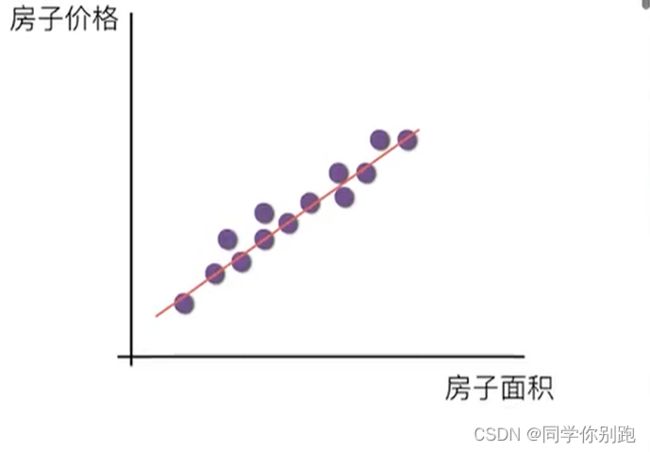
- 房价预测 --目标值:房价
- 销售额度预测 --目标值:销售额度
- 金融:贷款额度预测、利用线性回归以及系数分析因子
3)什么是线性回归
线性回归(Linear regression)是利用回归方程(函数) 对一个或多个自变量(特征值) 和因变量(目标值) 之间关系进行建模的一种分析方式。
特点: 只有一个自变量的情况称为单变量回归,多于一个自变量情况的叫做多元回归
公式:
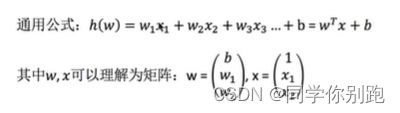
理解:
如图,特征值与目标值建立的关系==线性模型

4)线性回归的特征与目标的关系分析
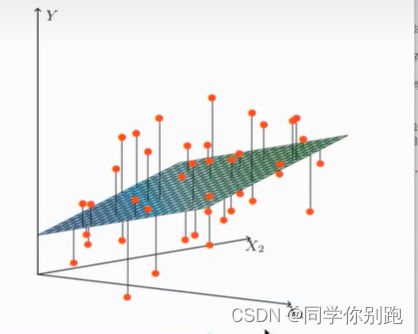
线性回归当中线性模型有两种,一种是线性关系,另一种是非线性关系。在这里我们只能画一个平面更好去理解,所以都用单个特征或两个特征举例子。
注释:单特征与目标值的关系呈直线关系,或者两个特征与目标值呈现平面的关系
总结:
- 线性关系一定是线性模型
- 线性模型不一定是线性关系
5)线性回归的损失和优化原理(理解记忆)
目标:求模型参数
模型参数能够使得预测准确
由于真实结果与预测结果之间存在一定的误差
->损失函数/成本函数/cost/目标函数

如何去减少这个损失,使我们预测的更加准确些? 既然存在了这个损失,我们一直说机器学习有自动学习的功能,在线性回归这里更是能够体现。这里可以通过一些优化方法去 优化 (其实是数学当中的求导功能) 回归的总损失!
->优化算法
如何去求模型当中的W,使得损失最小? (目的是找到最小损失对应的W值)线性回归经常使用的两种优化算法
正规方程 --天才


梯度下降(Gradient Descent) --勤奋努力普通人:不断试错、改进

理解:a为学习速率,需要手动指定
(超参数),a旁边的整体表示方向沿着这个函数下降的方向找,最后就能找到山谷的最低点,然后更新W值使用:面对训练数据规模十分庞大的任务,能够找到较好的结果
6)线性回归API
sklearn.linear_model.LinearRegression(fit_intercept=True)
- 通过正规方程优化
- fit_intercept:是否计算偏置
- LinearRegression.coef_: 回归系数
- LinearRegression.intercept_: 偏置
sklearn.linear_model.SGDRegressor(loss="squared _loss", fit_intercept=True,learning_rate ='invscaling', eta0=0.01)
- SGDRegressor类实现了随机梯度下降学习,它支持不同的loss函数和正则0化惩罚项来拟合线性回归模型。
- loss:损失类型
- loss=”squared_loss”:普通最小二乘法。 fit_intercept:是否计算偏置
- learning_rate :string, optional
学习率填充
‘constant’: eta = eta0
optimal’: eta = 1.0 / (alpha * (t + t0)) [default]invscaling’: eta = eta0 / pow(t, power_t)power_t=0.25:存在父类当中
-对于一个常数值的学习率来说,可以使用learning_rate=’constant’并使用eta0来指定学习率
-SGDRegressor.coef_: 回归系数
-SGDRegressorintercept_: 偏置
二、过拟合、欠拟合
学习目标
- 说明线性回归(不带正则化)的缺点
- 说明过拟合与欠拟合的原因以及解决方法
1)什么是过拟合、欠拟合?
在训练集上表现好,但测试集不好 – 过拟合
欠拟合
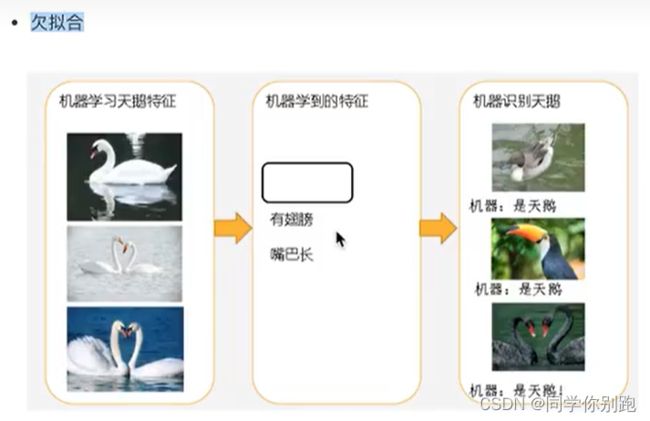
过拟合

定义
过拟合: 一个假设在训练数据上能够获得比其他假设更好的拟合,但是在测试数据集上却不能很好地拟合数据,此时认为这个假设出现了过拟合的现象。(模型过于复杂)
欠拟合: 一个假设在训练数据上不能获得更好的拟合,并且在测试数据集上也不能很好地拟合数据,此时认为这个假设出现了欠拟合的现象。(模型过于简单)
2)原因及解决办法
欠拟合:
原因: 学习到数据的特征过少
解决办法: 增加数据的特征数量
过拟合:
原因: 原始特征过多,存在一些嘈杂特征,模型过于复杂是因为模型尝试去兼顾各个测试数据点
解决办法: 正则化
在学习的时候,数据提供的特征有些影响模型复杂度或者这个特征的数据点异常较多,所以算法在学习的时候尽量减少这个特征的影响 (甚至删除某个特征的影响),这就是正则化
注:调整时候,算法并不知道某个特征影响,而是去调整参数得出优化的结果
三、岭回归
学习目标:
- 说明岭回归的原理即与线性回归的不同之处说明正则化对于权重参数的影响
- 说明L1和L2正则化的区别
1)定义
岭回归,其实也是一种线性回归。只不过在算法建立回归方程时候,加上L2正则化的限制,从而达到解决过拟合的效果
sklearn.linear_model.Ridge(alpha=1.0, fit_intercept=True,solver="auto"normalize=False)
- 具有12正则化的线性回归
- alpha:正则化力度,也叫入 取值: 0~1, 1~10
- solver:会根据数据自动选择优化方法
- sag:如果数据集、特征都比较大,选择该随机梯度下降优化
- normalize:数据是否进行标准化
- normalize=False:可以在fit之前调用
- preprocessing.StandardScaler标准化数据
- Ridge.coef_: 回归权重
- Ridge.intercept_: 回归偏置
四、分类算法:逻辑回归与二分类
学习目标:
- 说明逻辑回归的损失函数
- 说明逻辑回归的优化方法 说明sigmoid函数
- 知道逻辑回归的应用场景知道精确率、召回率指标的区别
- 知道F1-score指标说明召回率的实际意义
- 说明如何解决样本不均衡情况下的评估
- 了解ROC曲线的意义说明AUC指标大小。
- 应用classification_report实现精确率、召回率计算
- 应用roc_auc_score实现指标计算
1)逻辑回归的应用场景
- 广告点击率
- 是否为垃圾邮件
- 是否患病
- 金融诈骗
- 虚假账号
看到上面的例子,我们可以发现其中的特点,那就是都属于两个类别之间的判断。逻辑回归就是解决二分类问题的利器。
2)逻辑回归原理

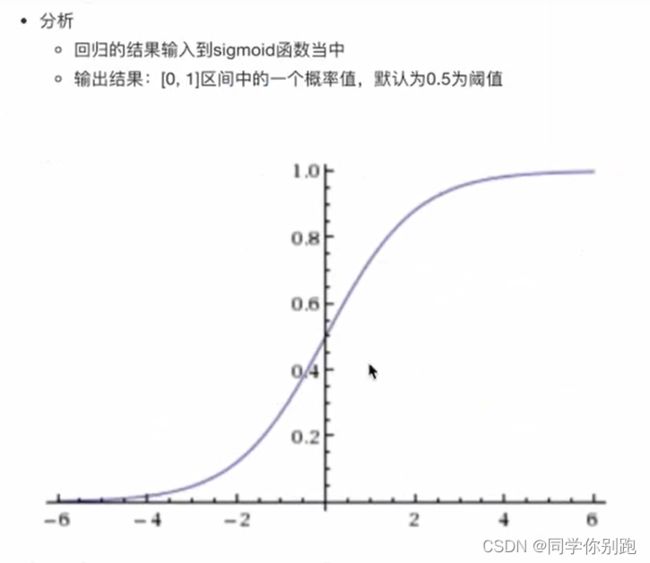
输出结果解释(重要): 假设有两个类别A,B,并且假设我们的概率值为属于A(1)这个类别的概率值。现在有一个样本的输入到逻辑回归输出结果0.6,那么这个概率值超过0.5,意味着我们训练或者预测的结果就是A(1)类别。那么反之,如果得出结果为0.3那么,训练或者预测结果就为B(0)类别
所以接下来我们回忆之前的线性回归预测结果我们用均方误差衡量那如果对于逻辑回归,我们预测的结果不对该怎么去衡量这个损失呢?我们来看这样一张图

那么如何去衡量逻辑回归的预测结果与真实结果的差异呢?
3)损失及优化
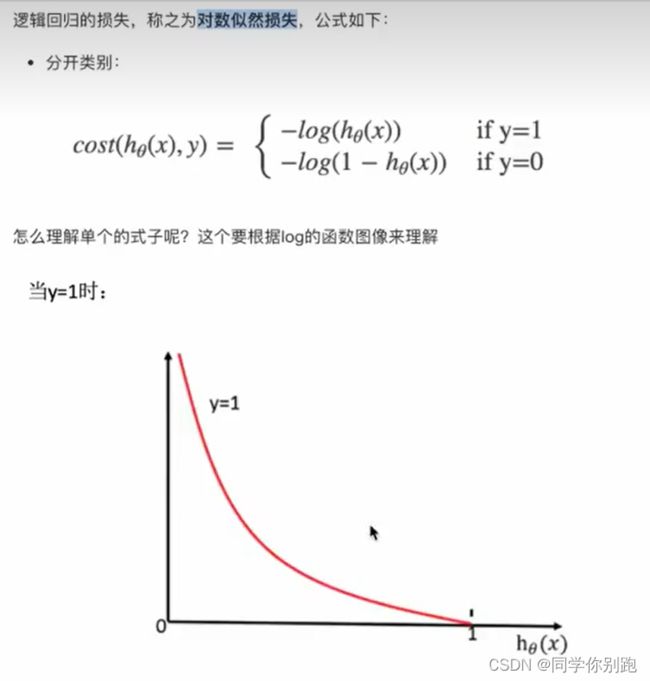


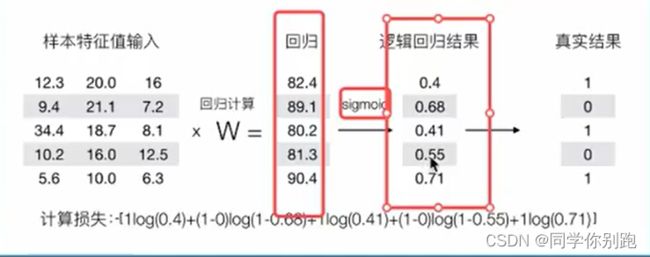
优化
同样使用梯度下降优化算法,去减少损失函数的值。这样去更新逻辑回归前面对应算法的权重参数,提升原本属于1类别的概率,降低原本是0类别的概率。
4)逻辑回归API
sklearn.linear_model.LogisticRegression(solver='liblinear',penalty=‘l2’,C=1.0)
- solver:优化求解方式(默认开源的liblinear库实现,内部使用了飞标轴下降法来迭代优化损失函数)
- sag: 根据数据集自动选择,随机平均梯度下降。penalty:正则化的种类
- C: 正则化力度
默认将类别数量少的当做正例
LogisticRegression方法相当于 SGDClassifier(loss=“log”, penalty=“”),SGDClassifier实现了一个普通的随机梯度下降学习也支持平均随机梯度下降法 (ASGD),可以通过设置average=True。而使gisticRegression(实现了SAG)
5)分类的评估方法
精确率与召回率
1混滑矩阵
在分类任务下,预测结果(Predicted Condition)与正确标记(Tue Condition)之间存在四种不同的组合,构成混滑矩阵(适用于多分类)

TP = True Possitive
FN = False Negative
召回率: 真实为正例的样本中预测结果为正例的比例 (查得全,对正样本的区分
能力)

3)分类评估报告API
sklearn.metrics.classification_report(y_true, y_pred, labels=[],target_names=None)
- y_true:真实目标值
- y_pred:估计器预测目标值
- labels:指定类别对应的数字
- target_names:目标类别名称
- return:每个类别精确率与召回率
五、模型保存与加载
由于每次得到模型都需要重新运行一遍,故需要进行模型保存。
sklearn模型的保存和加载API
from sklearn.externals import joblib
- 保存: joblib.pump(rf,‘test.pkl’)
- 加载: estimator = joblib.load(‘test.pkl’)
六、无监督学习-K-means算法
学习目标
- 说明K-means算法原理
- 说明K-means的性能评估标准轮廓系数
- 说明K-means的优缺点
1)什么是无监督学习
无目标值的一类问题
- 一家广告平台需要根据相似的人口学特征和购买习惯将美国人口分成不同的小组,以便广告客户可以通过有关联的广告接触到他们的目标客户。
- Airbnb需要将自己的房屋清单分组成不同的社区,以便用户能更轻松地查阅这些清单。
- 一个数据科学团队需要降低一个大型数据集的维度的数量,以便简化建模和降低文件大小。
我们可以怎样最有用地对其进行归纳科分组? 我们可以怎样以一种压缩格式有效地表征数据?这都是无监督学习的目标,之所以称之为无监督,是因为这是从无标签的数据开始学习的。
2)无监督学习包含的算法
- 聚类
K-means(K均值聚类) - 降维
PCA
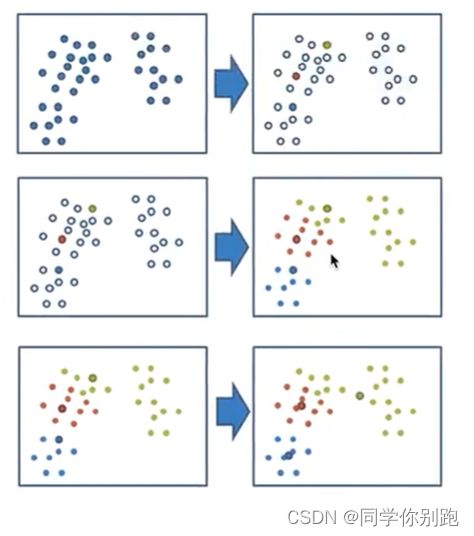
3)K-means聚类步骤
1、随机设置K个特征空间内的点作为初始的聚类中心
2、对于其他每个点计算到K个中心的距离,未知的点选择最近的一个聚类中心点作为标记类别
3、接着对着标记的聚类中心之后,重新计算出每个聚类的新中心点 (平均值)
4、如果计算得出的新中心点与原中心点一样,那么结束,否则重新进行第二步过程
4)K-means API
sklearn.cluster.KMeans(n_clusters=8,init='k-means++')
- k-means聚类
- n_clusters:开始的聚类中心数量
- init:初始化方法,默认为 ‘k-means ++’
- labels_:默认标记的类型,可以和真实值比较 (不是值比较)
sklearn.metrics.silhouette_score(X, labels)
- 计算所有样本的平均轮廓系数
- X:特征值
- labels:被聚类标记的目标值
7)用户聚类结果评估
silhouette_score(cust, pre)
8)K-means总结
特点分析:采用迭代式算法直观易懂,并且非常实用
缺点:容易收敛到局部最优解(多次聚类)
聚类在分类之前