因子分析-python3实现

实验原始数据

自己敲一下data.xlsx，别人博客的数据，我用的自己业务数据不好分享

实现代码

import pandas as pd
import numpy as np
import numpy.linalg as nlg
import matplotlib.pyplot as plt
from factor_analyzer import FactorAnalyzer, calculate_kmo, calculate_bartlett_sphericity  
 
def ZscoreNormalization(x):
    x = (x - x.mean(0)) / x.std(0)
    return x

def Norm_tchr(x):
    x = (x - x.min(0) + abs(x.max(0))) / (x.max(0) - x.min(0) + 2 * abs(x.max(0)))
    return x
    
def main():
    excelFile = 'data.xlsx'
    df=pd.DataFrame(pd.read_excel(excelFile))
    df2=df.copy()
    print("\n原始数据:\n",df2)
    del df2['ID']
    #对数据进行归一化操作
    df2 = pd.DataFrame(ZscoreNormalization(df2))
    
    # 皮尔森相关系数
    df2_corr=df2.corr()
    print("\n相关系数:\n",df2_corr)
 
    kmo = calculate_kmo(df2)  # KMO做主成分分析效度检验指标KMO0.9上非常合适做因子分析：0.8-0.9之间适合：0.7-0.8之间适合：0.6-0.7之间尚可：0.5-0.6之间表示差：0.5下应该放弃
    bartlett = calculate_bartlett_sphericity(df2)  # bartlett球形度检验p值要小于0.05
    print("\n因子分析适用性检验:")
    print('kmo:{},bartlett:{}'.format(kmo[1], bartlett[1]))
 
    fa = FactorAnalyzer(rotation=None, n_factors=15, method='principal')
    fa.fit(df2)
    fa_15_sd = fa.get_factor_variance()
    fa_15_df = pd.DataFrame(
        {'特征值': fa_15_sd[0], '方差贡献率': fa_15_sd[1], '方差累计贡献率': fa_15_sd[2]})
 
    #各个因子的特征值以及方差贡献率
    print("\n",fa_15_df)
 
    #一般选择方差累计贡献率大于0.85的公因子数
    # 确定最合适的公因子数目
    factor_num = 1
   while (True):
       factor_num += 1
       fa = FactorAnalyzer(rotation='promax', n_factors=factor_num, method='principal')
       fa.fit(data)
       fa_sd = fa.get_factor_variance()
       fa_df = pd.DataFrame({'特征值': fa_sd[0], '方差贡献率': fa_sd[1], '方差累计贡献率': fa_sd[2]})
       total_contribute = fa_df.iloc[factor_num - 1, 2]
         if total_contribute > 0.85:
           break
 
    #查看公因子提取度
    print("\n公因子提取度:\n",fa_5.get_communalities())
 
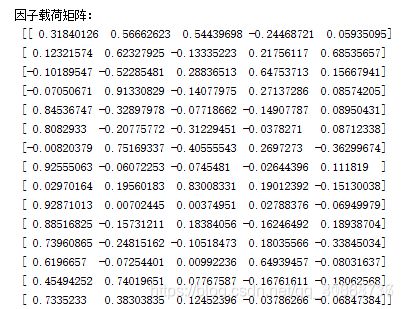
    #查看因子载荷
    print("\n因子载荷矩阵:\n",fa_5.loadings_)
 
    #使用最大方差法旋转因子载荷矩阵
    fa_rotate = FactorAnalyzer(rotation='varimax', n_factors=factor_num, method='principal')
    fa_rotate.fit(df2)
 
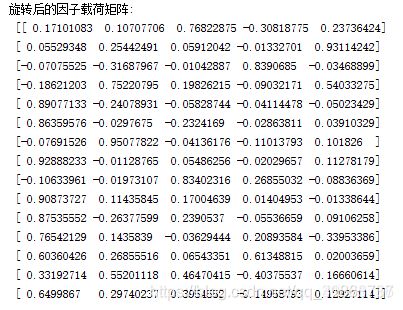
    #查看旋转后的因子载荷
    print("\n旋转后的因子载荷矩阵:\n",fa_5_rotate.loadings_)
 
    # 因子得分（回归方法）（系数矩阵的逆乘以因子载荷矩阵）
    X1 = np.mat(df2_corr)
    X1 = nlg.inv(X1)
 
    #B=(R-1)*A  15*5
    factor_score = np.dot(X1,fa_rotate.loadings_)
    factor_score = pd.DataFrame(factor_score)
    tmp_columns = []
    for index in range(factor_num):
       tmp = "factor" + str(index + 1)
       tmp_columns.append(tmp)
    factor_score.columns = tmp_columns
    print("\n因子得分：\n", factor_score)
 
    #F=XB  27*15 15*5=  27 5
    fa_t_score = np.dot(np.mat(df2), np.mat(factor_score))
    print("\n应试者的五个因子得分：\n",pd.DataFrame(fa_t_score))
 
 
    # 综合得分(加权计算）
    total_contribute = 0.0
    wei = []
    for index in range(factor_num):
        tmp = [float(fa_df.iloc[index, 1])]
        wei.append(tmp)
        total_contribute += float(fa_df.iloc[index, 1])
    fa_t_score = np.dot(fa_t_score, wei) / total_contribute  # 除以总的方差累积贡献率
    fa_t_score = pd.DataFrame(fa_t_score)
    fa_t_score.columns = ['综合得分']
    fa_t_score.insert(0, 'ID', range(1, 28))
    print("\n综合得分：\n", fa_t_score)
    print("\n综合得分：\n", fa_t_score.sort_values(by='综合得分', ascending=False).head())
 
    ax1=plt.subplot(111)
    X=fa_t_score['ID']
    Y=fa_t_score['综合得分']
    plt.bar(X, Y, color="red")
    plt.title('result00')
    ax1.set_xticks(range(len(fa_t_score)))
    ax1.set_xticklabels(fa_t_score.index)
    plt.show()
 
    fa_t_score1=pd.DataFrame()
    fa_t_score1=fa_t_score.sort_values(by='综合得分',ascending=False).head()
    X1 = fa_t_score1['ID']
    Y1 = fa_t_score1['综合得分']
    plt.bar(X1, Y1, color='red')
    plt.title('result01')
    plt.show()
 
if __name__ == '__main__':
    main()

kmo = BB/(AA+BB)
AA：所有变量之间 两两（不包括变量自己与自己）的偏相关系数的平方和【X和Y的偏相关系数：X和Z线性回归得到的残差Rx 与 Y和Z线性回归得到的残差Ry 之间的简单(peason)相关系数。这里的"Z"代表其他所有的变量】
BB：所有变量之间 两两（不包括变量自己与自己）的相关系数的平方和

当所有变量间的简单相关系数平方和远远大于偏相关系数平方和时，KMO值接近1。KMO值越接近于1,意味着变量间的相关性越强，原有变量越适合作因子分析；
当所有变量间的简单相关系数平方和接近0时，KMO值接近0.KMO值越接近于0,意味着变量间的相关性越弱，原有变量越不适合作因子分析。

bartlett球形度检验
巴特利特球形检验的公式，作以下说明：
H0：原始数据的相关系数矩阵R与同维度的单位矩阵一致；H1：……不一致。
χ2=-[n-(2p+11)/6]ln|R|; df=p(p-1)/2。
其中：n是数据记录的条数；p是因子分析的变量数目；ln（）是自然对数函数；|R|是相关系数矩阵R的行列式的值。
算出上述χ2统计量的值，查表χ2（0.01,df），若χ2<χ2（a,df）则拒绝H0而认可H1，即各变量之间相关，反之就不适合作因子分析。

因子分析是指通过少数不相关的因子反映多个具有相关性的原始信息，起到降维和剔除相关性的作用。因子分析的前提是具有一定的相关性，因此必须通过了kmo和bartlett球形度检验的数据才能进行因子分析。kmo值要大于0.7，bartlett球形度检验p值要小于0.05，则认为通过了适用性检验后进行因子分析。

进行因子分析，格式为：FactorAnalyzer(rotation= None,n_factors=n,method=‘principal’)

（1）rotation:旋转的方式，包括None:不旋转,‘varimax’:最大方差法,‘promax’：最优斜交旋转；

（2）n_factors:公因子的数量；

（3）method:因子分析的方法，包括’minres’:最小残差因子法,‘principal’:主成分分析法；

查看15个公因子的特征值以及方差贡献率，一般选择方差累计贡献率大于0.85的公因子（0.841246），于是接着根据5个公因子重新拟合。

查看公因子的提取度，发现当使用5个公因子时，5个公因子对15个维度的解释率都超过0.6，说明提取的5个公因子对原始维度有一定的解释力。