多元线性回归 python
Video Link
影片连结
This episode expands on Implementing Simple Linear Regression In Python. We extend our simple linear regression model to include more variables.
本集扩展了在Python中实现简单线性回归的方法 。 我们扩展了简单的线性回归模型以包含更多变量。
You can view the code used in this Episode here: SampleCode
您可以在此处查看 此剧 集中使用的代码: SampleCode
Setting up your programming environment can be found in the first section of Ep 4.3.
可以在Ep 4.3的第一部分中找到设置您的编程环境的步骤 。
导入我们的数据 (Importing our Data)
The first step is to import our data into python.
第一步是将我们的数据导入python。
We can do that by going on the following link: Data
我们可以通过以下链接进行操作: 数据
Click on “code” and download ZIP.
单击“代码”并下载ZIP。
Locate WeatherDataM.csv and copy it into your local disc under a new file ProjectData
找到WeatherDataM.csv并将其复制到新文件ProjectData下的本地磁盘中
Note: Keep this medium post on a split screen so you can read and implement the code yourself.
注意:请将此帖子张贴在分屏上,以便您自己阅读和实现代码。
Now we are ready to implement our code into our Notebook:
现在我们准备将代码实现到笔记本中:
# Import Pandas Library, used for data manipulation
# Import matplotlib, used to plot our data
# Import nump for mathemtical operationsimport pandas as pd
import matplotlib.pyplot as plt
import numpy as np# Import our WeatherDataM and store it in the variable weather_data_mweather_data_m = pd.read_csv("D:\ProjectData\WeatherDataM.csv")
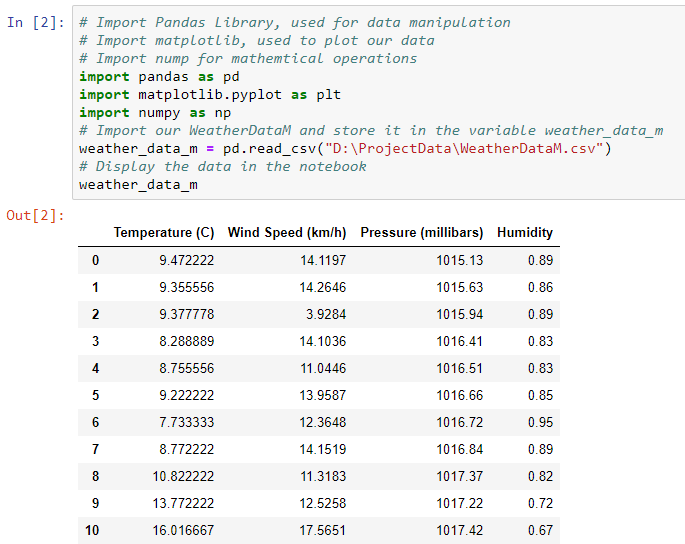
# Display the data in the notebookweather_data_mHere we can see a table with all the variables we will be working with.
在这里,我们可以看到一个包含所有要使用的变量的表。
绘制数据 (Plotting our Data)
Each of our inputs X (Temperature, Wind Speed and Pressure) must form a linear relationship with our output y (Humidity) in order for our multiple linear regression model to be accurate.
我们的每个输入X(温度,风速和压力)必须与我们的输出y(湿度)形成线性关系,以便我们的多元线性回归模型准确。
Let’s plot our variables to confirm this.
让我们绘制变量以确认这一点。
Here we follow common Data Science convention, naming our inputs X and output y.
在这里,我们遵循通用的数据科学约定 ,将输入X和输出y命名为。
# Set the features of our model, these are our potential inputsweather_features = ['Temperature (C)', 'Wind Speed (km/h)', 'Pressure (millibars)']# Set the variable X to be all our input columns: Temperature, Wind Speed and PressureX = weather_data_m[weather_features]# set y to be our output column: Humidityy = weather_data_m.Humidity# plt.subplot enables us to plot mutliple graphs
# we produce scatter plots for Humidity against each of our input variablesplt.subplot(2,2,1)
plt.scatter(X['Temperature (C)'],y)
plt.subplot(2,2,2)
plt.scatter(X['Wind Speed (km/h)'],y)
plt.subplot(2,2,3)
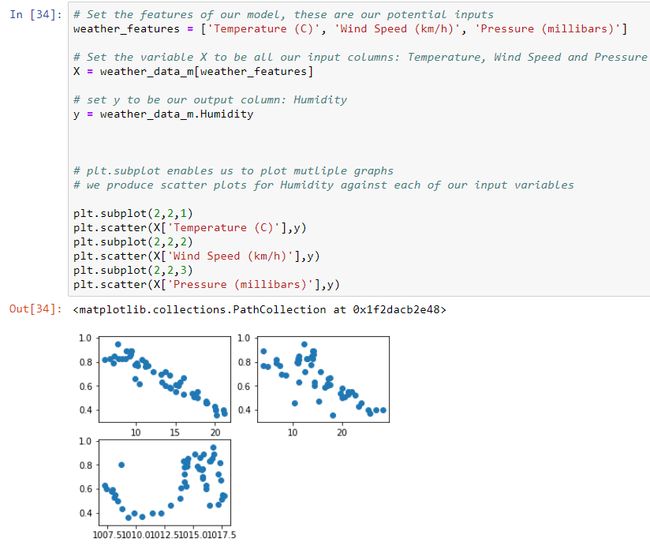
plt.scatter(X['Pressure (millibars)'],y)Humidity against Temperature forms a strong linear relationship ✓
相对于温度的湿度形成很强的线性关系 ✓
Humidity against Wind Speed forms a linear relationship ✓
湿度与风速成线性关系 ✓
Humidity against Pressure forms no linear relationship ✗
相对于压力的湿度没有线性关系 ✗
Pressure can not be used in our model and is removed with the following code
压力无法在我们的模型中使用,并通过以下代码删除
X = X.drop("Pressure (millibars)", 1)We specify the the column name went want to drop: Pressure (millibars)
我们指定要删除的列名称: 压力(毫巴)
1 represents our axis number: 1 is used for columns and 0 for rows.
1代表我们的轴号:1代表列,0代表行。
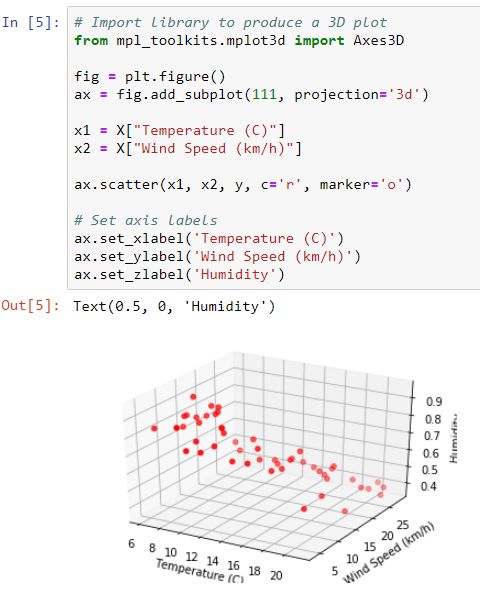
Because we are working with just two input variables we can produce a 3D scatter plot of Humidity against Temperature and Wind speed.
因为我们仅使用两个输入变量,所以可以生成湿度相对于温度和风速的3D散点图 。
With more variables this would not be possible, as this would require a 4D + plot which we as humans can not visualise.
有了更多的变量,这将是不可能的,因为这将需要我们人类无法看到的4D +图。
# Import library to produce a 3D plotfrom mpl_toolkits.mplot3d import Axes3Dfig = plt.figure()
ax = fig.add_subplot(111, projection='3d')x1 = X["Temperature (C)"]
x2 = X["Wind Speed (km/h)"]ax.scatter(x1, x2, y, c='r', marker='o')# Set axis labelsax.set_xlabel('Temperature (C)')
ax.set_ylabel('Wind Speed (km/h)')
ax.set_zlabel('Humidity')实现多元线性回归 (Implementing Multiple Linear Regression)
In order to calculate our Model we need to import the LinearRegression model from Sci-kit learn library. This function enables us to calculate the parameters for our model (θ₀, θ₁ and θ₂) with one line of code.
为了计算我们的模型,我们需要从Sci-kit学习库中导入LinearRegression模型。 此功能使我们能够使用一行代码来计算模型的参数 ( θ₀,θ₁和θ2) 。
from sklearn.linear_model import LinearRegression# Define the variable mlr_model as our linear regression model
mlr_model = LinearRegression()
mlr_model.fit(X, y)We can then display the values for θ₀, θ₁ and θ₂:
然后我们可以显示θ₀,θ和θ2的值:
θ₀ is the intercept
θ₀是截距
θ₁ and θ₂ are what we call co-efficients of the model as the come before our X variables.
θ₁和θ²是我们所谓的模型系数 ,即X变量之前的系数。
theta0 = mlr_model.intercept_
theta1, theta2 = mlr_model.coef_theta0, theta1, theta2Giving our multiple linear regression model as:
给出我们的多元线性回归模型为:
ŷ = 1.14–0.031¹- 0.004²
ŷ= 1.14–0.031¹-0.004²
使用我们的回归模型进行预测 (Using our Regression Model to make predictions)
Now we have calculated our Model, it’s time to make predictions for Humidity given a Temperature and Wind speed value:
现在我们已经计算了模型,是时候根据温度和风速值对湿度进行预测了:
y_pred = mlr_model.predict([[15, 21]])
y_predSo a temperature of 15 °C and Wind speed of 21 km/h expects to give us a Humidity of 0.587.
因此,温度为15°C,风速为21 km / h,预计湿度为0.587。
边注 (Side note)
We reshaped all of our inputs into 2D arrays by using double square brackets ( [[]] ) which is a much more efficient method.
我们使用双方括号([[]])将所有输入重塑为2D数组,这是一种更为有效的方法。
如果您有任何疑问,请将其留在下面,希望在下一集见。 (If you have any questions please leave them below and I hope to see you in the next episode.)
翻译自: https://medium.com/ai-in-plain-english/implementing-multiple-linear-regression-in-python-1364fc03a5a8
多元线性回归 python