(补)算法训练Day15 | LeetCode226. 翻转二叉树(10种遍历方式的应用);LeetCode101. 对称二叉树(考查遍历两个二叉树)
目录
LeetCode226. 翻转二叉树
1. 思路
2. 代码实现
2.1 递归法实现(前中后序)
2.2 迭代法(前中后序)
2.3 统一迭代法
2.4 层序遍历实现
3. 复杂度分析
4. 思考
LeetCode101. 对称二叉树
方法一:递归解法
1. 思路
2. 代码实现
3. 复杂度分析
4. 思考
方法二:迭代解法
1. 思路
2. 代码实现
实现方式一:使用队列迭代
实现方式二:使用栈迭代
3. 复杂度分析
4. 思考
LeetCode226. 翻转二叉树
链接: 226. 翻转二叉树 - 力扣(LeetCode)
1. 思路
我们之前介绍的都是各种方式遍历二叉树,这次要翻转了,感觉还是有点懵逼。
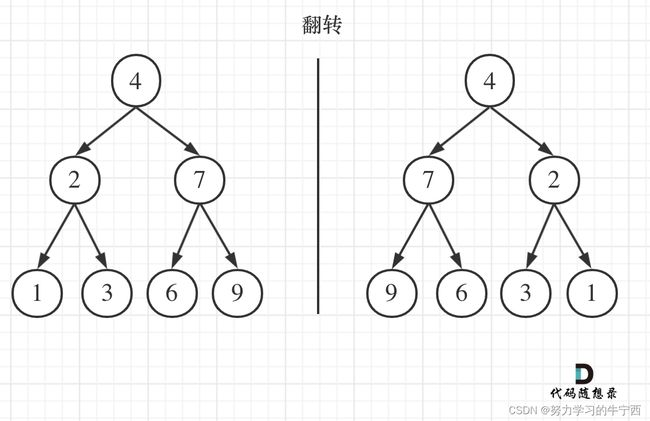
这得怎么翻转呢?如果要从整个树来看,翻转还真的挺复杂,整个树以中间分割线进行翻转,如图:
可以发现想要翻转它,其实就把每一个节点的左右孩子交换一下就可以了。
关键在于遍历顺序,前中后序应该选哪一种遍历顺序? (一些同学这道题都过了,但是不知道自己用的是什么顺序)
遍历的过程中只要把每一个节点的左右孩子翻转一下,就可以达到整体翻转的效果。这道题目使用前序遍历和后序遍历都可以,唯独中序遍历不方便,因为中序遍历(递归法)会把某些节点的左右孩子翻转了两次!建议拿纸画一画,就理解了。那么层序遍历可以不可以呢?依然可以的!只要把每一个节点的左右孩子翻转一下的遍历方式都是可以的!
中序遍历为啥不行?
以上面的二叉树为例,中序为左中右,先处理4的左孩子,把1和3交换顺序之后,再处理中节点,把2及其子树和7及其子树交换位置,现在该处理右节点了,但是发现右节点是之前处理过了的节点2及其子树,所以节点2及其子树会交换两遍,节点7及其子树没有处理。
2. 代码实现
用遍历二叉树的各种方法都可以实现,一共有10种。
包括递归法(前中后序)迭代法(前中后序)统一迭代法(前中后序)层序遍历
这里以前序递归为例实现:
# 前序递归实现 翻转二叉树 中左右
# time:O(N);space:O(N)
class Solution(object):
def invertTree(self, root):
"""
:type root: TreeNode
:rtype: TreeNode
"""
if root == None: return # base case
root.left, root.right = root.right,root.left #中
self.invertTree(root.left) # 左
self.invertTree(root.right) # 右
return root2.1 递归法实现(前中后序)
# 翻转二叉树 递归法
# Definition for a binary tree node.
# class TreeNode(object):
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
# 递归 前序遍历
class Solution(object):
def invertTree(self, root):
"""
:type root: TreeNode
:rtype: TreeNode
"""
if root == None: return None
root.left,root.right = root.right,root.left
self.invertTree(root.left)
self.invertTree(root.right)
return root
# 递归 后序遍历
class Solution(object):
def invertTree(self, root):
"""
:type root: TreeNode
:rtype: TreeNode
"""
if root == None: return None
self.invertTree(root.left)
self.invertTree(root.right)
root.left,root.right = root.right,root.left
return root
# 递归 中序遍历
# time:O(N) space:O(logN)
class Solution(object):
def invertTree(self, root):
"""
:type root: TreeNode
:rtype: TreeNode
"""
if root == None: return None
self.invertTree(root.left)
root.left,root.right = root.right,root.left
# 这里还是要翻转左孩子,因为上面左右互换了
self.invertTree(root.left)
return root2.2 迭代法(前中后序)
# 迭代法 前序遍历
# time:O(N);space:O(N)
class Solution(object):
def invertTree(self, root):
"""
:type root: TreeNode
:rtype: TreeNode
"""
if root == None: return None
stack = [root]
while stack:
node = stack.pop()
node.left,node.right = node.right,node.left
if node.right: stack.append(node.right)
if node.left: stack.append(node.left)
return root
# 迭代法 中序遍历
# time O(N) space:O(N)
class Solution(object):
def invertTree(self, root):
"""
:type root: TreeNode
:rtype: TreeNode
"""
if root == None: return None
stack = []
cur = root
while cur or stack:
if cur:
stack.append(cur)
cur = cur.left
else:
cur = stack.pop()
cur.left,cur.right = cur.right,cur.left
# 前面左右顺序换了,所以这里还是处理左孩子
cur = cur.left
return root
# 迭代法 后序遍历
# time:O(N);space:O(N)
class Solution(object):
def invertTree(self, root):
"""
:type root: TreeNode
:rtype: TreeNode
"""
if root == None: return None
stack = [root]
while stack:
node = stack.pop()
node.left,node.right = node.right,node.left #中
if node.right: stack.append(node.right) #右
if node.left: stack.append(node.left) #左
return root2.3 统一迭代法
# 统一迭代法 前序
# time:o(n) space:O(N)
class Solution(object):
def invertTree(self, root):
"""
:type root: TreeNode
:rtype: TreeNode
"""
if root == None: return None
stack = [root]
while stack:
node = stack.pop()
if node != None:
if node.right: stack.append(node.right)
if node.left: stack.append(node.left)
stack.append(node)
stack.append(None)
else:
node = stack.pop()
node.left,node.right = node.right,node.left
return root
# 统一迭代法 中序
# time:o(n) space:O(N)
class Solution(object):
def invertTree(self, root):
"""
:type root: TreeNode
:rtype: TreeNode
"""
if root == None: return None
stack = [root]
while stack:
node = stack.pop()
if node != None:
if node.right: stack.append(node.right)
stack.append(node)
stack.append(None)
if node.left: stack.append(node.left)
else:
node = stack.pop()
node.left,node.right = node.right,node.left
return root
# 统一迭代法 后序
# time:o(n) space:O(N)
class Solution(object):
def invertTree(self, root):
"""
:type root: TreeNode
:rtype: TreeNode
"""
if root == None: return None
stack = [root]
while stack:
node = stack.pop()
if node != None:
stack.append(node)
stack.append(None)
if node.right: stack.append(node.right)
if node.left: stack.append(node.left)
else:
node = stack.pop()
node.left,node.right = node.right,node.left
return root
2.4 层序遍历实现
# 层序遍历 迭代
class Solution(object):
def invertTree(self, root):
"""
:type root: TreeNode
:rtype: TreeNode
"""
if root == None: return None
from collections import deque
queue = deque([root])
while queue:
size = len(queue)
for _ in range (size):
node = queue.popleft()
node.left,node.right = node.right,node.left
if node.left: queue.append(node.left)
if node.right: queue.append(node.right)
return root3. 复杂度分析
本题的复杂度分析和二叉树的十种遍历方式的分析一模一样,可以参考。
4. 思考
- 所有写法的中序遍历如果按照原来遍历二叉树的方式写都是不可以的,因为这样会让某些节点的左右孩子翻转两次,如果非要用中序遍历的方式写也可以,在处理” 左中右“ 的”右“的时候,仍然写”左“ ,因为此时的右是实际上的左,具体代码实现可以看上面代码;
- 但是在用统一迭代的方式写的中序遍历是可以的,不变的;为什么这个中序就是可以的呢,因为这是用栈来遍历,而不是靠指针来遍历,避免了递归法中翻转了两次的情况,可以画图理解一下,这里有点意思的;
- 针对二叉树的问题,解题之前一定要想清楚究竟是前中后序遍历,还是层序遍历。**二叉树解题的大忌就是自己稀里糊涂的过了(因为这道题相对简单),但是也不知道自己是怎么遍历的。**这也是造成了二叉树的题目“一看就会,一写就废”的原因。
Reference: 代码随想录 (programmercarl.com)
本题学习时间: 60分钟。
LeetCode101. 对称二叉树
链接: 101. 对称二叉树 - 力扣(LeetCode)
方法一:递归解法
1. 思路
首先想清楚,判断对称二叉树要比较的是哪两个节点,要比较的可不是左右节点!对于二叉树是否对称,要比较的是根节点的左子树与右子树是不是相互翻转的,理解这一点就知道了其实我们要比较的是两个树(这两个树是根节点的左右子树),所以在递归遍历的过程中,也是要同时遍历两棵树。
那么如何比较呢?
比较的是两个子树的里侧和外侧的元素是否相等。如图所示:
那么遍历的顺序应该是什么样的呢?
本题遍历只能是“后序遍历”,因为我们要通过递归函数的返回值来判断两个子树的内侧节点和外侧节点是否相等。
具体来说是因为要不断收集左右孩子的信息,返回给上一个节点,不断返回,才最后知道左子树和右子树是否可以相互翻转,后序遍历中,最后“中”的处理,就是将左右孩子的信息向上返回了;
如果是前序遍历,中左右,上来就在处理中间节点了,左右还没处理,我咋知道左边子树是否和右边子树相互翻转;同理中序遍历信息也不完善。
两个子树的遍历顺序一样吗?
**因为要遍历两棵树而且要比较内侧和外侧节点,所以准确的来说是一个树的遍历顺序是左右中,一个树的遍历顺序是右左中。**但都可以理解算是后序遍历,尽管已经不是严格上在一个树上进行遍历的后序遍历了。
2. 代码实现
递归三部曲
- 确定递归函数的参数和返回值
因为我们要比较的是根节点的两个子树是否是相互翻转的,进而判断这个树是不是对称树,所以要比较的是两个树,参数自然也是左子树节点和右子树节点。
返回值自然是bool类型。
代码如下:
def compare(self, left, right):
- 确定终止条件
要比较两个节点数值相不相同,首先要把两个节点为空的情况弄清楚!否则后面比较数值的时候就会操作空指针了。
节点为空的情况有:
(注意我们比较的其实不是左孩子和右孩子,所以如下我称之为左节点右节点)
- 左节点为空,右节点不为空,不对称,return false
- 左不为空,右为空,不对称 return false
- 左右都为空,对称,返回true
此时已经排除掉了节点为空的情况,那么剩下的就是左右节点不为空:
- 左右都不为空,比较节点数值,不相同就return false
此时左右节点不为空,且数值也不相同的情况我们也处理了。
代码如下:
if left == None and right != None: return False
elif left != None and right == None: return False
elif left == None and right == None: return True
#排除了空节点,再排除数值不相同的情况
elif left.val != right.val: return False
注意上面最后一种情况,我没有使用else,而是elseif, 因为我们把以上情况都排除之后,剩下的就是 左右节点都不为空,且数值相同的情况。
- 确定单层递归的逻辑
此时才进入单层递归的逻辑,单层递归的逻辑就是处理 左右节点都不为空,且数值相同的情况。
- 比较二叉树外侧是否对称:传入的是左节点的左孩子,右节点的右孩子。
- 比较内测是否对称,传入左节点的右孩子,右节点的左孩子。
- 如果左右都对称就返回true ,有一侧不对称就返回false 。
代码如下:
#此时就是:左右节点都不为空,且数值相同的情况
#此时才做递归,做下一层的判断
outside = self.compare(left.left, right.right) #左子树:左、 右子树:右
inside = self.compare(left.right, right.left) #左子树:右、 右子树:左
isSame = outside and inside #左子树:中、 右子树:中 (逻辑处理)
return isSame
如上代码中,我们可以看出使用的遍历方式,左子树左右中,右子树右左中,所以我把这个遍历顺序也称之为“后序遍历”(尽管不是严格的后序遍历)。
最后递归的Python整体代码如下:
# time:O(N);space:O(N)
class Solution:
def isSymmetric(self, root: TreeNode) -> bool:
if not root:
return True
return self.compare(root.left, root.right)
def compare(self, left, right):
#首先排除空节点的情况
if left == None and right != None: return False
elif left != None and right == None: return False
elif left == None and right == None: return True
#排除了空节点,再排除数值不相同的情况
elif left.val != right.val: return False
#此时就是:左右节点都不为空,且数值相同的情况
#此时才做递归,做下一层的判断
#左子树:左、 右子树:右
outside = self.compare(left.left, right.right)
#左子树:右、 右子树:左
inside = self.compare(left.right, right.left)
#左子树:中、 右子树:中 (逻辑处理)
isSame = outside and inside
return isSame
给出的代码并不简洁,但是把每一步判断的逻辑都清楚的描绘出来了。
如果上来就看网上各种简洁的代码,看起来真的很简单,但是很多逻辑都掩盖掉了,而题解可能也没有把掩盖掉的逻辑说清楚。**盲目的照着抄,结果就是:发现这是一道“简单题”,稀里糊涂的就过了,但是真正的每一步判断逻辑未必想到清楚。**当然我可以把如上代码整理如下:
class Solution:
def isSymmetric(self, root: TreeNode) -> bool:
if not root: return True
return self.compare(root.left, root.right)
def compare(self, left, right):
if left == None and right != None: return False
elif left != None and right == None: return False
elif left == None and right == None: return True
elif left.val != right.val: return False
else return self.compare(left.left, right.right) and
self.compare(left.right, right.left)
这个代码就很简洁了,但隐藏了很多逻辑,条理不清晰,而且递归三部曲,在这里完全体现不出来。所以建议大家做题的时候,一定要想清楚逻辑,每一步做什么。把道题目所有情况想到位,相应的代码写出来之后,再去追求简洁代码的效果。
3. 复杂度分析
假设树上一共 N 个节点。
时间复杂度:这里遍历了这棵树,时间复杂度为 O(n); 空间复杂度:这里的空间复杂度和递归使用的栈空间有关,这里递归层数不超过 n,故空间复杂度为 O(n)。
4. 思考
- 本题考查同时处理两个二叉树的遍历;
- 二叉树的题目,确定遍历顺序是非常重要的一个问题,决定你对这道题的理解深度;
- 收集左右孩子信息再向上返回的这类题目,都需要采用后序遍历的做法
- 关键是要将题意转换成 ” 要比较的是根节点的左子树和右子树是否是相互翻转的“。
方法二:迭代解法
1. 思路
这道题目我们也可以使用迭代法,但要注意,这里的迭代法可不是前中后序的迭代写法,因为本题的本质是判断两个树是否是相互翻转的,其实已经不是所谓二叉树遍历的前中后序的关系了。
主要思路是把左右两个子树要比较的元素顺序放进一个容器,然后成对成对的取出来进行比较。
2. 代码实现
实现方式一:使用队列迭代
这里我们可以使用队列来比较两个树(根节点的左右子树)是否相互翻转,(注意这不是层序遍历)
# 迭代法 用队列
class Solution(object):
def isSymmetric(self, root):
"""
:type root: TreeNode
:rtype: bool
"""
if root == None: return True
from collections import deque
queue = deque()
queue.append(root.left) #将左子树头结点加入队列
queue.append(root.right) #将右子树头结点加入队列
while queue: #接下来就要判断这这两个树是否相互翻转
leftNode = queue.popleft()
rightNode = queue.popleft()
#左节点为空、右节点为空,此时说明是对称的
if leftNode == None and rightNode == None: continue
# 因为这是迭代的做法,所以不能直接return True 应该要继续比较
elif leftNode != None and rightNode == None: return False
elif leftNode == None and rightNode != None: return False
elif leftNode.val != rightNode.val: return False
else:
queue.append(leftNode.left) #加入左节点左孩子
queue.append(rightNode.right) #加入右节点右孩子
queue.append(leftNode.right) #加入左节点右孩子
queue.append(rightNode.left) #加入右节点左孩子
return True
实现方式二:使用栈迭代
其实使用栈也是可以的。只要把队列原封不动的改成栈就可以了
# 迭代法 使用栈
# time:o(N);space:o(N)
class Solution(object):
def isSymmetric(self, root):
"""
:type root: TreeNode
:rtype: bool
"""
if root == None: return True
stack = []
stack.append(root.right)
stack.append(root.left)
while stack:
leftNode = stack.pop()
rightNode = stack.pop()
if not leftNode and not rightNode: continue
# 上面那三行的判断可以简略为这一行判断
elif not leftNode or not rightNode or
leftNode.val != rightNode.val:
return False
else:
stack.append(leftNode.left)
stack.append(rightNode.right)
stack.append(leftNode.right)
stack.append(rightNode.left)
return True
3. 复杂度分析
时间复杂度:O(N)
N为二叉树的节点数目,这里遍历了这颗二叉树,因此时间复杂度为O(N);
空间复杂度:O(N)
这里需要用一个队列/栈来维护节点,每个节点最多进队一次,出队一次,队列中最多不会超过 n 个点,故空间复杂度为 O(n)。
4. 思考
- 我们深度剖析了一道二叉树的“简单题”,大家会发现,真正的把题目搞清楚其实并不简单,leetcode上accept了和真正掌握了还是有距离的。
- 我们介绍了递归法和迭代法,递归依然通过递归三部曲来解决了这道题目,如果只看精简的代码根本看不出来递归三部曲是如果解题的。
- 在迭代法中我们使用了队列,需要注意的是这不是层序遍历,而且仅仅通过一个容器来成对的存放我们要比较的元素,知道这一本质之后就发现,用队列,用栈,甚至用数组,都是可以的。
- 这两道题目基本和本题是一样的,只要稍加修改就可以AC。(还没做)
- 100.相同的树
- 572.另一个树的子树
- 注意:左右节点都为空的时候,不能像递归法一样直接return True ;这是迭代做法,应该继续比较,因为queue此时不一定为空了,如果继续之后发现queue为空,会跳出while循环,return True。
Reference: 代码随想录 (programmercarl.com)
本题学习时间: 60分钟。
本篇的学习大约花了2小时,总字数9500+,在学习完二叉树的10种遍历方式之后,本篇的翻转二叉树是对10种遍历方式的应用;对称二叉树是同时遍历两个二叉树的应用。(求推荐!)