剑指OFFER DAY9

第 9 天

动态规划 Dynamic programming

---

 剑指 Offer 42. 连续子数组的最大和

 

动态规划五个步骤

1. 确定dp[i]数组以及下标i的含义
2. 推导状态转移方程式/递归公式
3. 数组初始化，确定dp[0]的值
4. 确定遍历顺序，递推公式中dp[i]依赖于dp[i - 1]的状态，需要从前向后遍历；反之亦然
5. 举例推导dp数组前几个，与代码输出结果相验证   

• 如果打印出来和自己预先模拟推导是一样的，那么就是自己的递归公式、初始化或者遍历顺序有问题了。

• 如果和自己预先模拟推导的不一样，那么就是代码实现细节有问题。

这次我们用动态规划的思路再来分析一次。

动规五部曲如下：

1:  确定dp数组（dp table）以及下标的含义

dp[i]：包括下标i之前的最大连续子序列和为dp[i]。

2: 确定递推公式

dp[i]只有两个方向可以推出来：

• dp[i - 1] + nums[i]，即：nums[i]加入当前连续子序列和
• nums[i]，即：从头开始计算当前连续子序列和

一定是取最大的，所以dp[i] = max(dp[i - 1] + nums[i], nums[i]);

3: dp数组如何初始化

从递推公式可以看出来dp[i]是依赖于dp[i - 1]的状态，dp[0]就是递推公式的基础。

dp[0]应该是多少呢?

根据dp[i]的定义，很明显dp[0]应为nums[0]即dp[0] = nums[0]。

4: 确定遍历顺序

递推公式中dp[i]依赖于dp[i - 1]的状态，需要从前向后遍历。

5: 举例推导dp数组

以示例一为例，输入：nums = [-2,1,-3,4]，对应的dp状态如下：

dp = [-2,1,-2,4] 

 打印结果发现一致，表示可能没有问题

以下给出代码

class Solution:
    def maxSubArray(self, nums: List[int]) -> int:
        n = len(nums)
        dp = [0]*n
        dp[0] = nums[0]
        for i in range(1,n):
            dp[i] = max(dp[i-1]+nums[i],nums[i])
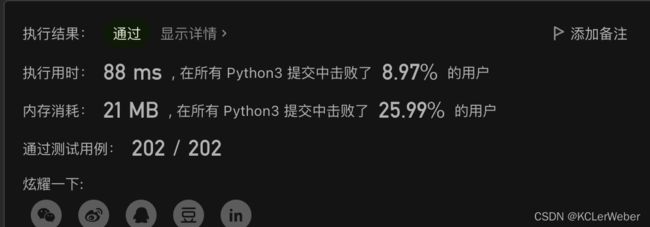
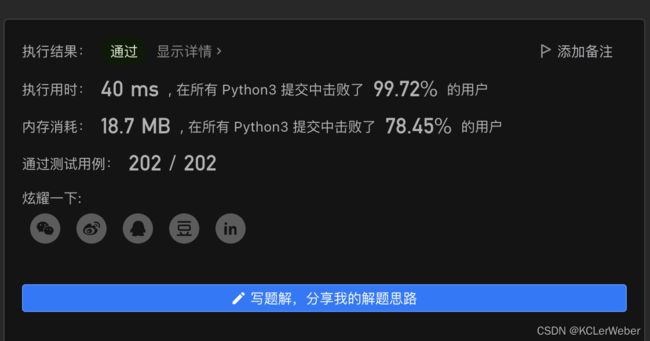
        return max(dp)

 

---

下面我又做了一点优化，省去了数组结构，直接用res变量记录到目前为止最大的子数组的和，最后直接返回res即可，并增加了判断条件来替代用时过多的Max()方法，可以进一步减少时间消耗，结果在用时和内存消耗上得到了极大的提升。

class Solution:
    def maxSubArray(self, nums: List[int]) -> int:
        n = len(nums)
        dp = nums[0]
        res = dp
        for i in range(1,n):
            if dp > 0:
                dp = dp + nums[i]
            else:
                dp = nums[i]
            if dp > res:
                res = dp
        return res

 

这里我想插一个知识点，用if来判断两个数的大小是否比max()方法更快呢 

start = time.time()
a = 10
b = 100

if a > b:
    c = a
else:
    c = b

end = time.time()
print(end - start)


>>>9.5367431640625e-07

if 判断用时不稳定，有时候甚至会出现0.0的情况

start = time.time()
a = 10
b = 100
c = max(a,b)

end = time.time()
print(end - start)

>>>9.5367431640625e-07

而max()稳定在这个用时

贴个链接python 判断两数大小并赋值方法运行速度比较

当数字变多时max方法用时的确会更大

---

 大佬有一个原地改变数组的方法

class Solution:
    def maxSubArray(self, nums: List[int]) -> int:
        for i in range(1, len(nums)):
            nums[i] += max(nums[i - 1], 0)
        return max(nums)

---

剑指 Offer 47. 礼物的最大价值

这个题我的想法是遍历并原地替换棋盘中的值为到该点的最大值，这样右下角的值即为可以拿到最多礼物的价值。

代码如下

class Solution:
    def maxValue(self, grid: List[List[int]]) -> int:
        m = len(grid)
        n = len(grid[0])
        for x in range(m):
            for y in range(n):
                if x-1 >= 0 and y-1 >= 0:
                    up = grid[x-1][y]
                    left = grid[x][y-1]
                    if up>=left:
                        grid[x][y] = up+grid[x][y]
                    else:
                        grid[x][y] = left+grid[x][y]
                elif x-1 >= 0 and y-1 < 0:
                    up = grid[x-1][y]
                    grid[x][y] = up+grid[x][y]
                elif y-1 >= 0 and x-1 < 0:
                    left = grid[x][y-1]
                    grid[x][y] = left+grid[x][y]
        return grid[m-1][n-1]

 看了大佬的做法感觉思路一样但是代码逻辑更清晰

class Solution:
    def maxValue(self, grid: List[List[int]]) -> int:
        for i in range(len(grid)):
            for j in range(len(grid[0])):
                if i == 0 and j == 0: continue
                if i == 0: grid[i][j] += grid[i][j - 1]
                elif j == 0: grid[i][j] += grid[i - 1][j]
                else: grid[i][j] += max(grid[i][j - 1], grid[i - 1][j])
        return grid[-1][-1]

---

刷题心得：

在创建二维数组的时候，尽量使用下面这种方法

 m = [[0]*5 for i in range(3)]    #创建一个3行5列的二维数组

如果使用以下方法

 m = [[0]*5 ]*3

m只是3个空列表的引用

当你改变其中一个列表的某个索引时，三个列表都会同时改变