用数据讲故事：基于分析场景的17条Python使用小结

数据科学的编程需要非常灵活的语言，以最少的代码处理复杂的数据建模场景。作为一名数科小白，我对Python的第一认知是丰富的机器学习算法，但Python有超过12万个第三方库，覆盖从数据预处理、统计分析、数据挖掘及可视化等各种日常数据科学建模。本文对基础用法不做赘述，主要分享我在分析场景中常用的部分方法，供大家参考交流。

本文为该系列第二篇文章。

第一篇：用数据讲故事：13条Excel进阶技巧总结

数据预处理

▐  缺失值处理

包含均值/中位数/众数插补法、固定值插补法、最近邻插补法、回归法及剔除法等。

# 判断是否存在缺失值
print(data.info(),'\n')
data2=data.dropna(axis=0)

▐  异常值处理

包含剔除法、视为缺失值、平均值修正法等。

data=np.array(data)
# 计算上下四分位数
q1=np.quantile(data,q=0.25)
q3=np.quantile(data,q=0.75)
# 异常值判断标准，1.5倍的四分位差 计算上下须对应的值
low_quantile=q1-1.5*(q3-q1)
high_quantile=q3+1.5*(q3-q1)
data2=[]
for i in data:
    if i>high_quantile:
        i=high_quantile
        data2.append(i)
    elif i

▐  标准化处理

包含Min-max 标准化、z-score 标准化、Decimal scaling小数定标标准化三种，将原始数据转换为无量纲化，处于同一数量级别上。

(data - data.min()) / (data.max() - data.min())  # Min-max 标准化
(data - data.mean()) / data.std()  # z-score 标准化
data / 10 ** np.ceil(np.log10(data.abs().max()))  # Decimal scaling小数定标标准化

▐  连续变量重分类

等宽重编码：将一组连续性数据分段为0，(0,100]、(100,300]、(300,500]、(500,700]、(700,900]、(900,1100]、(1100,1300]、1300及以上9类。

等频重编码：将一组连续性数据按照25%分成4类。

#等宽重编码
bins = [0,100,200,300,500,700,900,1100,1300,max(df['data'])] #10个数，9个空格，产生9类
bins = [0,100,200,300,500,700,900,1100,1300,max(Wpop2['data'])]
df['col'] = pd.cut(df['data'],bins,right=True,labels=[1,2,3,4,5,6,7,8,9])


#等频重编码
k=4           
w = df['data'].quantile(np.arange(0,1+1/k,1/k))  
df['col'] = pd.cut(df['data'], w, right=True, labels=[1,2,3,4])

统计分析

▐  曲线拐点——KneeLocator

当我们寻找“最佳留存拐点”（如下图）或K-means聚类算法采用手肘法计算最佳K值时，python中有一个只要定义少量参数就可以帮我们寻找拐点的包kneed，参数定义如下：

x：待检测数据对应的横轴数据序列，如活跃天数

y：待检测数据序列，在x条件下对应的值，如6日回访率

S：float型，默认为1，敏感度参数，越小对应拐点被检测出得越快

curve：指明曲线之上区域是凸集还是凹集，concave代表凹，convex代表凸

direction：指明曲线初始趋势是增还是减，increasing表示增，decreasing表示减

from kneed import KneeLocator
import matplotlib.pyplot as plt 


x = np.arange(1,31)
y = [0.492 ,0.615 ,0.625 ,0.665 ,0.718 ,0.762 ,0.800 ,0.832 ,0.859 ,0.880 ,0.899 ,0.914 ,0.927 ,0.939 ,0.949 ,0.957 ,0.964 ,0.970 ,0.976 ,0.980 ,0.984 ,0.987 ,0.990 ,0.993 ,0.994 ,0.996 ,0.997 ,0.998 ,0.999 ,0.999 ]


kneedle = KneeLocator(x, y, S=1.0, curve='concave', direction='increasing')
print(f'拐点所在的x轴是: {kneedle.elbow}')

▐  相关系数——corr

corr主要计算两组数值型变量的相关性，数值越大相关性越强。求得相关性指数后，如何评价两变量从统计学角度具有相关性呢？我们可以将样本数与显著性因子输入相关系数临界值计算器中计算临界值，判断变量是否具有相关性。

《相关系数临界值计算器》地址：https://www.jisuan.mobi/vu11B3u3mb3NUUQQ.html

import pandas as pd
import numpy as np
s.corr() s
#输出相关系数矩阵s


s.corr()["pay_ord_cnt"] 
#输出pay_ord_cnt变量与其他变量之间的相关系数


s["pay_ord_cnt"].corr(s["pay_ord_amt"]) 
#输出"pay_ord_cnt"与"pay_ord_amt"之间的相关系数

▐  卡方检验——chi2_contingency

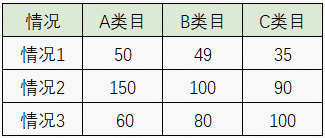
上述提到的相关系数是针对两组数值型变量，当变量是分类变量时或多变量时，变量之间的相关关系就不能简单地用此种方法。即使将分类变量变换成数值型变量，受转化的数值量级、取值标准等的影响，无法可靠地评估相关性大小的准确性。这时，卡方检验是一种多变量显著分析的方法，如分析类目与情况类型是否有关，提出两个假设：

原假设（H0）：类目与情况类型无关

备择假设（H1）：类目与情况类型有关

from scipy.stats import chi2_contingency
import numpy as np


df= np.array([[50,49,35], [150,100,90],[60,80,100]])
kt=chi2_contingency(df)


print('卡方值=%.4f, p值=%.4f, 自由度=%i expected_frep=%s'%kt)


#卡方值=27.7029, p值=0.0000, 自由度=4 expected_frep=[[ 48.79551821  42.97759104  42.22689076]
#[123.80952381 109.04761905 107.14285714]
#[ 87.39495798  76.97478992  75.6302521 ]]

通过计算，P值小于0.01，则拒绝原假设，认为类目与情况类型有关。

▐  线性回归——polyfit

对于数据科学来讲，线性回归是统计建模和预测分析的出发点，我们常用线性回归模型观测变量趋势，然后再匹配模型。Python中实现线性回归模型的方法有多种，除了基于最小二乘多项式的numpy.polyfit，还有Stats.linregress、Optimize.curve_fit、numpy.linalg.lstsq、Statsmodels.OLS 、sklearn.linear_model.LinearRegression等，可结合数据情况使用。

import numpy
from numpy import polyfit
x=[x for x in range(1,len(y)+1)]
y=[int(res) for res in y]
res=polyfit(x,y,deg=1)
return numpy.float(res[0])

数据挖掘

▐  综合规模的排序打分——Wilson_Score

我们常遇到评价多个商品点击率的好坏或者评估AB-TEST上线后的效果，在小样本情况下直接用比率指标难免偏颇，如商品A曝光100次，点击20次，商品B曝光10次，单击3次，商品B的点击率未必比商品A好，所以需要引入威尔逊区间的修正公式，解决小样本的准确性问题，再利用贝叶斯平均提供补偿值，平衡样本数量的差异。

u：正例数（点击） V：负例数（未点击） n：实例总数（曝光总数） p：点击率 z：是正态分布的分位数  S：表示最终的威尔逊得分。

pos = float(input_data.split(',')[0])
        total = float(input_data.split(',')[1])
        p_z=1.96
        pos_rat = pos * 1. / total * 1.  #
        score = (pos_rat + (np.square(p_z) / (2. * total))
                 - ((p_z / (2. * total)) * np.sqrt(4. * total * (1. - pos_rat) * pos_rat + np.square(p_z)))) / \
                (1. + np.square(p_z) / total)
        return str(score)

▐  计算指标权重——PCA

除了探索性分析，我们最常见的业务场景就是通过数据建模的方法，分析各项指标对整体贡献情况，即权重。

主成分分析主要是基于降维思维，考虑各个指标的相互关系，通过正交变换转换成一组不相关的变量即主成分，计算指标不同主成分线性组合的系数确定权重。

import numpy as np
import pandas as pd
from sklearn.decomposition import PCA
from sklearn import preprocessing


# 数据标准化（还可选用StandardScaler、MaxAbsScaler、Normalizer进行标准化）
scaler = preprocessing.MinMaxScaler().fit(csv_df)
X_scaler = pd.DataFrame(scaler.transform(csv_df))


# 主成分分析建模
pca = PCA(n_components=None)  # n_components提取因子数量
# n_components=‘mle’，将自动选取主成分个数n，使得满足所要求的方差百分比
# n_components=None，返回所有主成分
pca.fit(X_scaler)
pca.explained_variance_  # 贡献方差，即特征根
pca.explained_variance_ratio_  # 方差贡献率
pca.components_  # 成分矩阵
k1_spss = pca.components_ / np.sqrt(pca.explained_variance_.reshape(-1, 1))  # 成分得分系数矩阵


# 确定权重
j = 0
Weights = []
for j in range(len(k1_spss)):
    for i in range(len(pca.explained_variance_)):
        Weights_coefficient = np.sum(100 * (pca.explained_variance_ratio_[i]) * (k1_spss[i][j])) / np.sum(
            pca.explained_variance_ratio_)
    j = j + 1
    Weights.append(np.float(Weights_coefficient))
print('Weights',Weights)


# 权重结果归一化
Weights=pd.DataFrame(Weights)
Weights1 = preprocessing.MinMaxScaler().fit(Weights)
Weights2 = Weights1.transform(Weights)
print('Weights2',Weights2)

▐  分词&词频——jieba/collection

jieba库是一款优秀的第三方中文分词库，jieba 支持三种分词模式：精确模式、全模式和搜索引擎模式。其中精准模式将语句最精确的切分，不存在冗余数据，适合做文本分析。我们也可以根据需求，批量添加自定义词典。

统计切分结果中的词频统计常使用collections包中的Counter方法。

import re                           # 正则表达式库
import jieba                        # 结巴分词
import jieba.posseg                 # 词性获取
import collections                  # 词频统计库
import numpy                        # numpy数据处理库


seg_list_exact = jieba.cut(string_data, cut_all=False, HMM=True)  # 精确模式分词+HMM


jieba.load_userdict("词典.txt") # 批量添加词典，utf-8编码


with open(StopWords, 'r', encoding='UTF-8') as meaninglessFile:
        stopwords = set(meaninglessFile.read().split('\n'))
    stopwords.add(' ')
    for word in seg_list_exact:  # 循环读出每个分词
        if word not in stopwords:  # 如果不在去除词库中
            object_list.append(word)  # 分词追加到列表


    # 词频统计
    word_counts = collections.Counter(object_list)  # 对分词做词频统计
    word_counts_top = word_counts.most_common(number)  # 获取前number个最高频的词
    return word_counts_top

▐  关键词提取——TF-IDF/TexTRank

文章关键词提取主要由两种函数，基于TF-IDF的extract_tags和基于TexTRank的textrank，原理如下：

TF-IDF：通过词频统计的方法得到某个词对一篇文档的重要性大小。以弱化常见词，保留重要的词，若某个词在某个文档中是高频词，在整个语料中又是低频出现，那么这个词将具有高TF-IDF值。

TexTRank：是一种基于图的用于关键词抽取和文档摘要的排序算法，利用一篇文档内部的词语间的共现信息(语义)便可以抽取关键词

from jieba import analyse
analyse.set_stop_words("停用词.txt") 
#TF-IDF
keywords = analyse.extract_tags(s, topK=20, withWeight=False) 
#TexTRank
keywords = analyse.textrank(content, topK=10, withWeight=False,allowPOS=('ns', 'n', 'vn', 'n'))

▐  情感分析——SnowNLP/TextBlob

有时我们需要分析商品评论的情感极性，SnowNLP、TextBlob是Python处理中、英文的类库，并自带了训练好的词典，支持分词、词性标注、情感分析、文本相似等多个功能，也支持训练新的模型进行情感分析。

• 中文情感分析

SnowNLP的情感分析取值，取值范围为[0,1]，表达的是“这句话代表正面情感的概率”。评论“感觉颜色暗了点，便宜，懒得退了“的情感取值为0.04为负向情感，“颜色很好看，很厚实，推荐指数10分”的情感取值是0.91为正向情感。

from snownlp import SnowNLP


s = SnowNLP(u'感觉颜色暗了点，便宜，懒得退了')  
print('分词结果:',s.words)          
print('这个评论为积极的概率:',s.sentiments)  


# 分词结果: ['感觉', '颜色', '暗', '了', '点', '，', '便宜', '，', '懒得', '退', '了']
# 这个评论为积极的概率: 0.04176293661978303




s = SnowNLP(u'颜色很好看，很厚实，推荐指数10分')  
print('分词结果:',s.words)          
print('这个评论为积极的概率:',s.sentiments)  


# 分词结果: ['颜色', '很', '好看', '，', '很', '厚实', '，', '推荐', '指数', '10', '分']
# 这个评论为积极的概率: 0.9093984931459346

• 英文情感分析

TextBlob的情感极性的变化范围是[-1, 1]，-1代表完全负面，1代表完全正面。

from textblob import TextBlob


s = TextBlob('I feel that the color is a little dark.I am too lazy to return')
print('这个评论的情感极性:',s.sentiment)  


# 这个评论的情感极性: Sentiment(polarity=-0.21875, subjectivity=0.75)


s = TextBlob('The color is very nice and thick, 10 points for recommendation index')
print('这个评论的情感极性:',s.sentiment)  


# 这个评论的情感极性: Sentiment(polarity=0.24, subjectivity=0.7375)

数据可视化

在数据分析时，经常需要对数据进行可视化，由于本人使用Python进行数据可视化经验有限，仅分享一些官方资源，供大家了解。

▐  Matplotlib

1. Matplotlib 安装（地址：https://matplotlib.org/stable/users/installing/index.html）

2. Matplotlib 用户手册（地址：https://matplotlib.org/stable/users/index.html）

3. Matplotlib 函数汇总（地址：https://matplotlib.org/stable/api/pyplot_summary.html）

4. Matplotlib 模块索引（地址：https://matplotlib.org/stable/py-modindex.html）

5. Matplotlib 示例库（地址：https://matplotlib.org/stable/gallery/index.html）

6. Matplotlib 示例下载

   Python code（地址：https://matplotlib.org/stable/gallery/index.html）

   Jupyter notebooks

▐  Seaborn

Seaborn 是基于 Python 且非常受欢迎的图形可视化库，在 Matplotlib 的基础上，进行了更高级的封装，使得作图更加方便快捷。

1. seaborn库的简介（地址：https://seaborn.pydata.org/）

2. seaborn库的安装 (地址：https://seaborn.pydata.org/installing.html）

3. seaborn库函数汇总（地址：https://seaborn.pydata.org/examples/errorband_lineplots.html）

PyODPS 及 Python UDF

上文主要介绍数据预处理、统计分析及挖掘的常用函数及用法。在数据量极大的情况下，手动写入或csv上传较为复杂，我们希望基于ODPS表调用Python第三方包。在进行临时数据探查时PyODPS是一种简单方便的方法，对需要调度上线的任务可以通过开发Pyhon UDF的方式进行调用。

▐  DSW 读取ODPS表

打开PAI-DSW进入实例进行开发

1. 安装PyODPS：pip install pyodps

2. 检查是否安装完成：python -c "from odps import ODPS"

3. 与ODPS建立链接，读取ODPS表

import numpy as np
import pandas as pd
from kneed import KneeLocator
import matplotlib.pyplot as plt
from odps import ODPS
from odps.df import DataFrame
# 建立链接。
o = ODPS(
    'AccessId', 
    'AccessKey', 
    '项目空间',
    endpoint='http://service-corp.odps.aliyun-inc.com/api')
# 读取ODPS表。
sql = '''
SELECT
    *
FROM
    项目空间.表名
;
'''
query_job = o.execute_sql(sql)
result = query_job.open_reader(tunnel=True) 
df = result.to_pandas(n_process=1)

# 读取ODPS表中列。
x =df['pay_ord_cnt']
y =df['pay_ord_amt']


# 调用KneeLocator包。
kneedle = KneeLocator(x, y, S=1.0, curve='convex', direction='increasing')
print(f'拐点所在的x轴是: {kneedle.elbow}')
;

▐  Python UDF开发

STEP1：在PyPI页面的Download files区域，单击文件名后缀为manylinux_2_5_x86_64.manylinux1_x86_64.whll的Numpy包进行下载。（确定资源包是编译过的wheel类型）

STEP2：修改下载的Numpy包后缀为ZIP格式

STEP3：传Numpy包至MaxCompute项目空间

方法一：在客户端输入命令：

ADD ARCHIVE D:\Downloads\numpy-1.19.2-cp37-cp37m-manylinux1_x86_64.zip -f;

方法二：数据开发-业务流程-Maxcompute-资源-新建-ARCHIVE（新建资源完成后记得提交）

STEP4：写UDF函数（以1.2.4线性回归函数为例）

from odps.udf import annotate
from odps.distcache import get_cache_archive


def include_package_path(res_name):
    import os, sys
    archive_files = get_cache_archive(res_name)
    dir_names = sorted([os.path.dirname(os.path.normpath(f.name)) for f in archive_files
                       if '.dist_info' not in f.name], key=lambda v: len(v))
    sys.path.append(os.path.dirname(dir_names[0]))


@annotate("*->float")   --输出类型
class Mypolyfit(object):
    def __init__(self):        
        include_package_path('numpy.zip')


    def evaluate(self, y):
        import numpy
        from numpy import polyfit
        x=[x for x in range(1,len(y)+1)]
        y=[int(res) for res in y]
        res=polyfit(x,y,deg=1)
        return numpy.float(res[0])

注：include_package_path 使得ODPS能够引入numpy包，并在主函数的_init_()部分使用

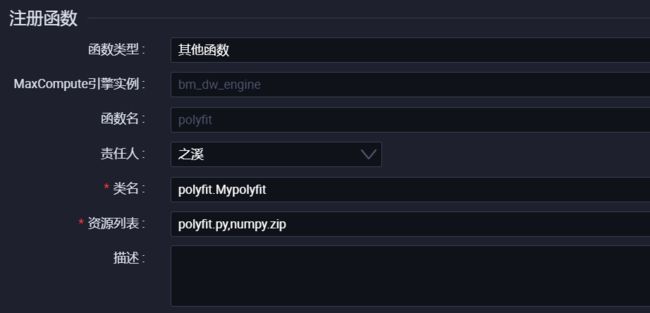
STEP5：注册函数

1. 类名=文件名.类名
   

2. 资源列表：python文件、调用包的文件名

STEP6：在sql中使用UDF函数

set odps.sql.python.version=cp37;
set odps.pypy.enabled=false;
set odps.isolation.session.enable = true;
set odps.sql.type.system.odps2=true;  
--sql使用UDF函数时要添加前三个参数设置
--如果UDF输出的是folat类型，要配合set odps.sql.type.system.odps2=true使用
select item_id,
       POLYFIT(pay_ord)
FROM
(select item_id
        ,SPLIT(regexp_replace(
        concat_ws('-',
                    sort_array(
                                collect_list(
                                            concat_ws(':',cast(ds as string),pay_ord_itm_qty_1d_001)
                                            )
                                )
                    ),'\\d+\:','') ,'-')
        pay_ord
        ,SPLIT(concat_ws('-',sort_array(collect_list(ds)) ),'-') as ds_array
FROM    table
WHERE   条件;

数据科学是一个横跨数学、统计学、机器学习、计算机的综合学科。在此先占个坑，后续也会将工作中更多理论与实践的结合更新到系列文章中，也欢迎数据爱好者一起交流学习。

团队介绍

我们是大聚划算数据科学团队，负责支持聚划算、百亿补贴、天天特卖等业务。我们聚焦优惠和选购体验，通过数据洞察，挖掘数据价值，建立面向营销场、服务供需两端的消费者运营和供给运营解决方案，我们与运营、产品合力，打造最具价格优惠心智的购物入口，最具爆发性的营销矩阵，让货品和心智运营变得高效且有确定性！

¤ 拓展阅读 ¤

3DXR技术 | 终端技术 | 音视频技术

服务端技术 | 技术质量 | 数据算法