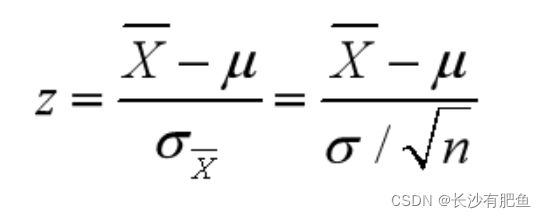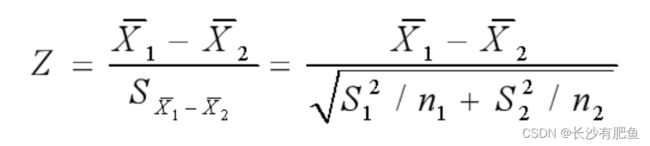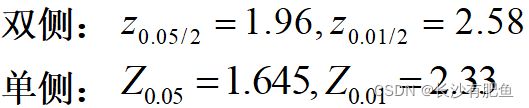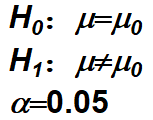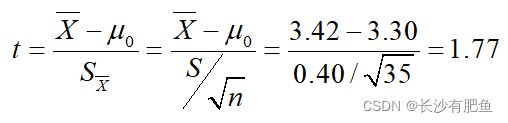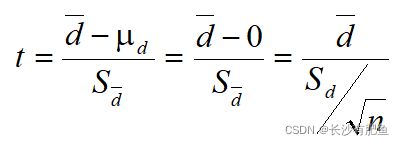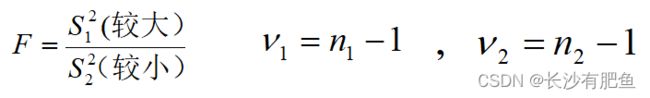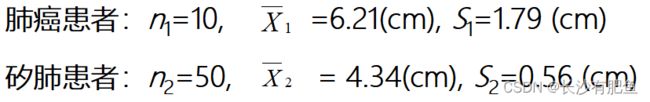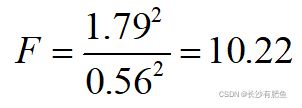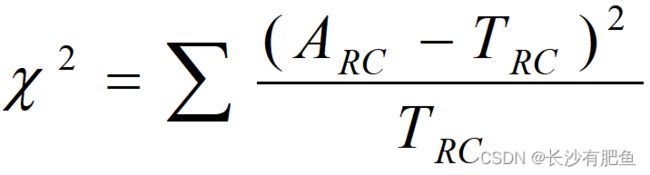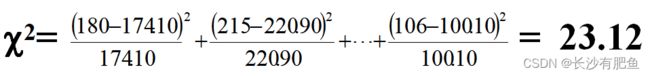假设检验总结

假设检验：

• 什么是假设：对总体参数（均值，比例等）的具体数值所作的陈述。比如，我认为新的配方的药效要比原来的更好。

• 什么是假设检验：先对总体的参数提出某种假设，然后利用样本的信息判断假设是否成立的过程。比如，上面的假设我是要接受还是拒绝呢。

假设检验的应用：

• 推广新的教育方案后，教学效果是否有所提高

• 醉驾判定为刑事犯罪后是否会使得交通事故减少

• 男生和女生在选文理科时是否存在性别因素影响

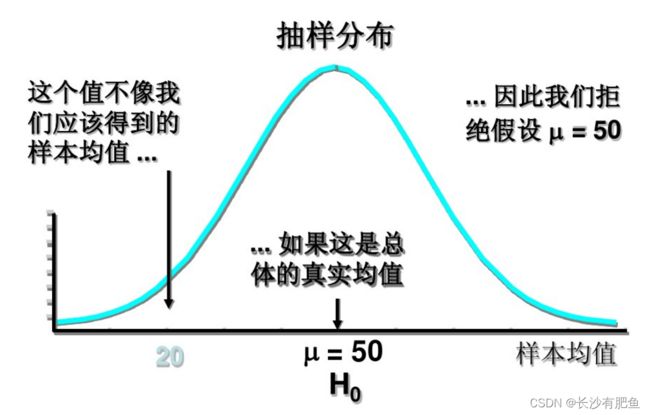
假设检验的基本思想：

显著性水平：

• 一个概率值，原假设为真时，拒绝原假设的概率，表示为 alpha 常用取值为0.01, 0.05, 0.10

• 一个公司要来招聘了，本来实际有200个人准备混一混，但是公司希望只有5%的人是浑水摸鱼进来的，所以可能会有200*0.05=4个人混进来，所谓显著性水平α，就是你允许最多有多大比例浑水摸鱼的通过你的测试。

假设检验的步骤：

• 提出假设
• 确定适当的检验统计量
• 规定显著性水平
• 计算检验统计量的值
• 做出统计决策

原假设与备择建设：

• 待检验的假设又叫原假设，也可以叫零假设，表示为H0。（零假设其实就是表示原假设一般都是说没有差异，没有改变。。。）
• 与原假设对比的假设叫做备择假设，表示为H1
• 一般在比较的时候，主要有等于，大于，小于

检验统计量：

• 计算检验的统计量
• 根据给定的显著性水平，查表得出相应的临界值
• 将检验统计量的值与显著性水平的临界值进行比较
• 得出拒绝或不拒绝原假设的结论

检验中常说的小概率：

• 在一次试验中，一个几乎不可能发生的事件发生的概率
• 在一次试验中小概率事件一旦发生，我们就有理由拒绝原假设
• 小概率由我们事先确定

P值：

• 是一个概率值
• 如果原假设为真，P-值是抽样分布中大于或小于样本统计量的概率
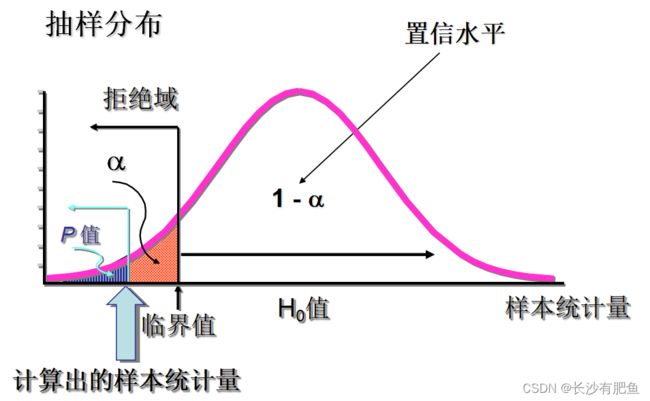
• 左侧检验时，P-值为曲线上方小于等于检验统计量部分的面积
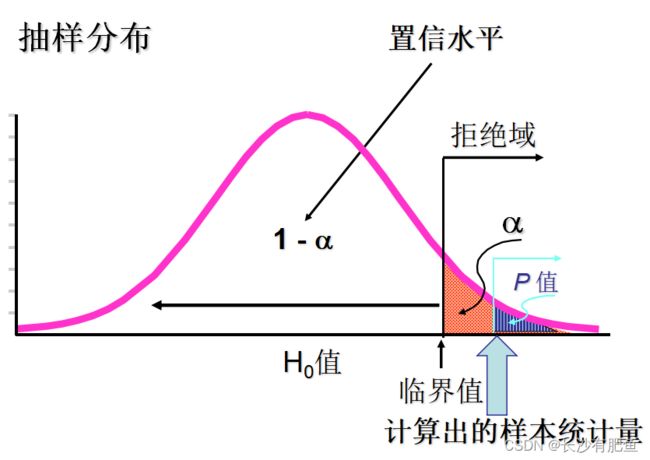
• 右侧检验时，P-值为曲线上方大于等于检验统计量部分的面积

左侧检验与右侧检验

• 当关键词有不得少于/低于的时候用左侧，比如灯泡的使用寿命不得少于/低于700小时时

• 当关键词有不得多于/高于的时候用右侧，比如次品率不得多于/高于5%时

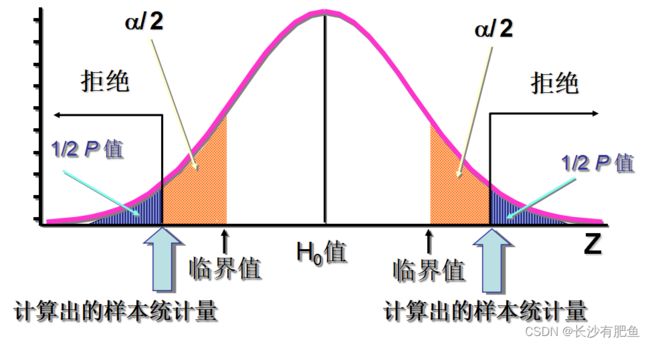
 双侧检验

• 单侧检验指按分布的一侧计算显著性水平概率的检验。用于检验大于、小于、高于、低于、优于、劣于等有确定性大小关系的假设检验问题。这类问题的确定是有一定的理论依据的。假设检验写作：μ1<μ2或μ1>μ2。

• 双侧检验指按分布两端计算显著性水平概率的检验， 应用于理论上不能确定两个总体一个一定比另一个大或小的假设检验。一般假设检验写作H1：μ1≠μ2。

例如，某种零件的尺寸，要求其平均长度为10cm，大于或小于10cm均属于不合格我们想要证明(检验)大于或小于这两种可能性中的任何一种是否成立 建立的原假设与备择假设应为：

H0: μ = 10 H1: μ ≠ 10

检验结果：

单侧检验

• 若p值 > α,不拒绝 H0
• 若p值 < α, 拒绝 H0

双侧检验

• 若p-值 > α/2, 不拒绝 H0
• 若p-值 < α/2, 拒绝 H0

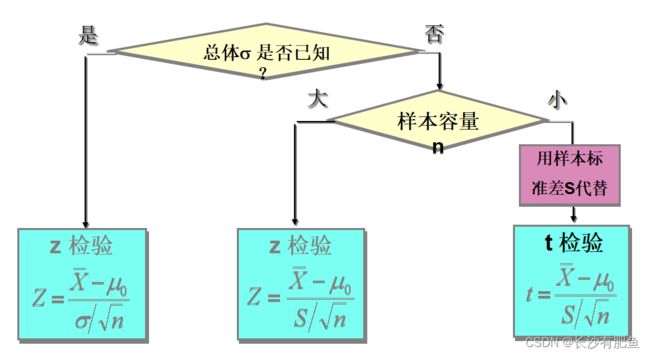
 总体均值检验

统计量Ｚ值的计算公式为：

如果检验一个样本平均数与一个已知的总体平均数的差异是否显著，其Z值计算公式为：

                           

 如果检验来自两个的两组样本平均数的差异性，从而判断它们各自代表的总体的差异是否显著，其Z值计算公式为：

Ｚ检验原理：

• 当总体标准差已知,样本量较大时用标准正态分布的理论来推断差异发生的概率，从而比较两个平均数的差异是否显著
• 标准正态变换后Ｚ的界值

                          

Z检验实例1：

              

                           

 确定P值, 作出推断结论 本例Ｚ=10.40>1.96（查表得0.975对应值），故P <0.05，按α=0.05水准拒绝H0，接受H1，可以认为正常人与高血压患者的血清胆固醇含量有差别，高血压患者高于正常人。

Z检验实例2：

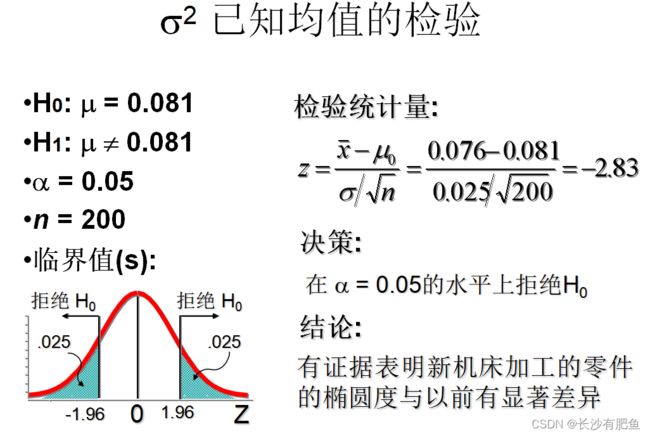
某机床厂加工一种零件，根据经验知道，该厂加工零件的椭圆度近似服从正态分布，其总体均值为μ=0.081mm，总体标准差为σ= 0.025 。今换一种新机床进行加工，抽取n=200个零件进行检验，得到的椭圆度为0.076mm。试问新机床加工零件的椭圆度的均值与以前有无显著差异？（α＝0.05）

 Z检验实例3：

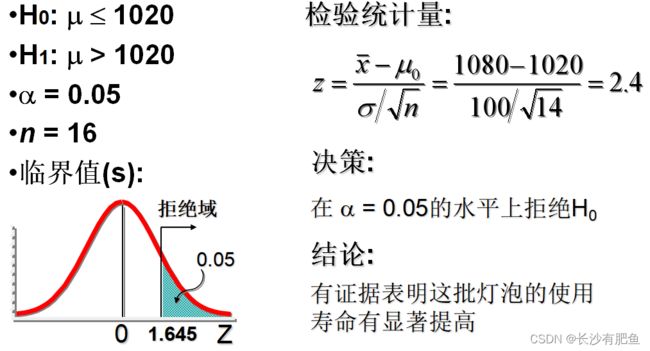
根据过去大量资料，某厂生产的灯泡的使用寿命服从正态分布N~(1020，100^2)。现从最近生产的一批产品中随机抽取16只，测得样本平均寿命为1080小时。试在0.05的显著性水平下判断这批产品的使用寿命是否有显著提高？(α＝0.05)

T检验：

根据研究设计,t检验有三种形式：

• 单个样本的t检验：

用来比较一组数据的平均值和一个数值有无差异。例如，你选取了5个人，测定了他们的身高，要看这五个人的身高平均值是否高于、低于还是等于1.70m，就需要用这个检验方法。

• 配对样本均数t检验(非独立两样本均数t检验)

用来看一组样本在处理前后的平均值有无差异。比如，你选取了5个人，分别在饭前和饭后测量了他们的体重，想检测吃饭对他们的体重有无影响，就需要用这个t检验。

• 两个独立样本均数t检验

用来看两组数据的平均值有无差异。比如，你选取了5男5女，想看男女之间身高有无差异，这样，男的一组，女的一组，这两个组之间的身高平均值的大小比较可用这种方法。

单个样本t检验

• 又称单样本均数t检验(one sample t test),适用于样本均数与已知总体均数μ0的比较,目的是检验样本均数所代表的总体均数μ是否与已知总体均数μ0有差别。
• 已知总体均数μ0一般为标准值、理论值或经大量观察得到的较稳定的指标值。
• 应用条件，总体标准α未知的小样本资料,且服从正态分布。

实例：

以往通过大规模调查已知某地新生儿出生体重为3.30kg。从该地难产儿中随机抽取35名新生儿,平均出生体重为3.42kg,标准差为0.40kg,问该地难产儿出生体重是否与一般新生儿体重不同?

• 建立检验假设，确定检验水准

                                                   

  计算检验统计量：

                 

本例自由度v=n-1=35-1=34，查表得得t0.05/2,34=2.032。 因为t < t0.05/2,34，故P>0.05，按 α=0.05水准，不拒绝H0，差别无统计学意义，尚不能认为该地难产儿与一般新生儿平均出生体重不同。 

配对样本均数t检验：

• 简称配对t检验(paired t  test),又称非独立两样本均数t检验,适用于配对设计计量资料均数的比较。
• 配对设计(paired design)是将受试对象按某些特征相近的原则配成对子，每对中的两个个体随机地给予两种处理。

配对样本均数t检验原理：

• 配对设计的资料具有对子内数据一一对应的特征,研究者应关心是对子的效应差值而不是各自的效应值。

• 进行配对t检验时，首选应计算各对数据间的差值d，将d作为变量计算均数。

• 配对样本t检验的基本原理是假设两种处理的效应相同，理论上差值d的总体均数μd 为0，现有的不等于0差值样本均数可以来自μd = 0的总体,也可以来μd ≠ 0的总体。

• 可将该检验理解为差值样本均数与已知总体均数μd（μd = 0）比较的单样本t检验,其检验统计量为：

                         

实例：

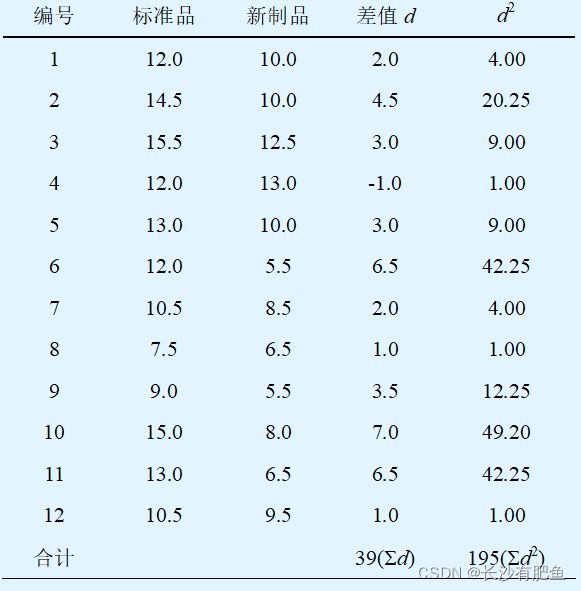
有12名接种卡介苗的儿童，8周后用两批不同的结核菌素，一批是标准结核菌素，一批是新制结核菌素，分别注射在儿童的前臂，两种结核菌素的皮肤浸润反应平均直径(mm)如表所示，问两种结核菌素的反应性有无差别。

       

               

              

两独立样本t检验

• 两独立样本t 检验(two independent sample t-test)，又称成组 t 检验。

• 适用于完全随机设计的两样本均数的比较,其目的是检验两样本所来自总体的均数是否相等。

• 完全随机设计是将受试对象随机地分配到两组中，每组患者分别接受不同的处理，分析比较处理的效应。

• 两独立样本t检验要求两样本所代表的总体服从正态分布N(μ1，σ^2)和N(μ2，σ^2)，且两总体方差σ1^2、σ2^2相等,即方差齐性。若两总体方差不等需要先进行变换

两独立样本t检验原理

两独立样本t检验的检验假设是两总体均数相等,即H0：μ1=μ2，也可表述为μ1－μ2=0,这里可将两样本均数的差值看成一个变量样本,则在H0条件下两独立样本均数t检验可视为样本与已知总体均数μ1－μ2=0的单样本t检验, 统计量计算公式为：

实例：

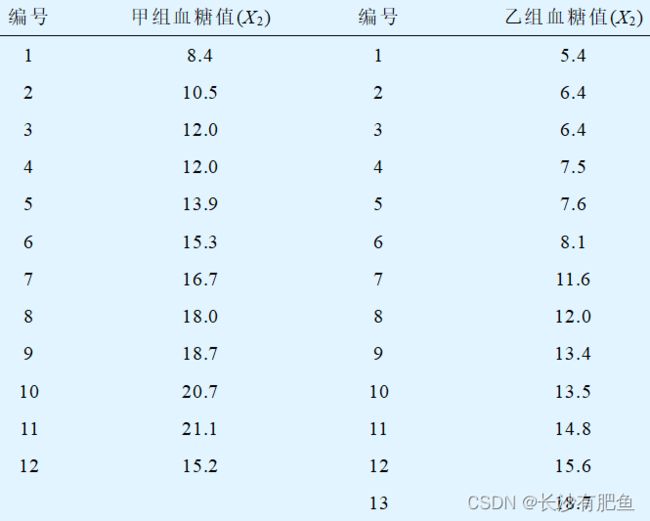
25例糖尿病患者随机分成两组，甲组单纯用药物治疗，乙组采用药物治疗合并饮食疗法，二个月后测空腹血糖(mmol/L)如表所示，问两种疗法治疗后患者血糖值是否相同？

 

T检验应用条件：

• 两组计量资料小样本比较
• 样本对总体有较好代表性，对比组间有较好组间均衡性——随机抽样和随机分组
• 样本来自正态分布总体，配对t检验要求差值服从正态分布，大样本时，用z检验，且正态性要求可以放宽
• 两独立样本均数t检验要求方差齐性——两组总体方差相等或两样本方差间无显著性

正态性检验和两总体方差的齐性检验

正态性检验

• 图示法：常用的图示法包括P-P图法和Q-Q图法。图中数据呈直线关系可认为呈正态分布，不呈直线关系可认为呈偏态分布。

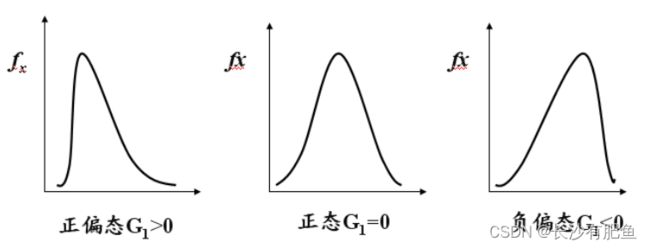
• 偏度检验：主要计算偏度系数，H0：G1=0，总体分布对称 H1：G1≠0，总体分布不对称。

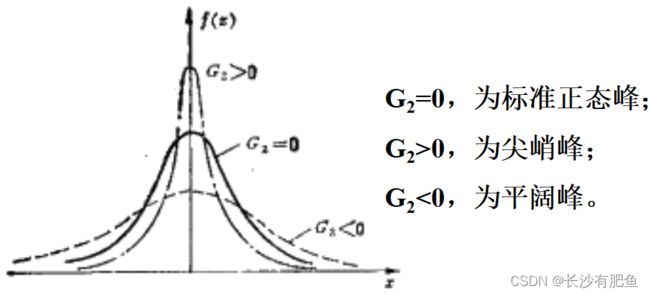
 峰度检验,主要计算峰度系数,H0：G2=0，总体分布为正态峰,H1：G2≠0，总体分布不是正态峰

 方差齐性检验

 式中S1^2为较大的样本方差S2^2为较小的样本方差，分子的自由度为v1，分母的自由度为v2，相应的样本例数分别为n1和n2 。F值是两个样本方差之比，如仅是抽样误差的影响，它一般不会离1太远，反之，F 值较大，两总体方差相同的可能性较小。F分布就是反映此概率的分布。求得F值后，查附表，F界值表得P值，Fα，不拒绝H0，可认为两总体方差相等； F≥Fα/2(ν1，ν2），则P≤α，拒绝H0，可认为两总体方差不等。

实例：

 （1）建立检验假设 ,确定检验水准

（2）计算F值

                               

（3）确定P值 作出推断结论 本例ν1=10-1=9，ν2=50-1=49，查附表，F界值表， F0.10/2(9,49）=2.80，得P＜0.05, 按α=0.10，拒绝H0, 接受H1，故可认为两总体方差不齐。

方差不齐时，两小样本均数的比较，可选用以下方法：① 采用近似法t‘检验; ② 采用适当的变量变换，使达到方差齐的要求; ③采用秩和检验。 

卡方检验(Chi-square test)

用于检验两个（或多个）率或构成比之间差别是否有统计学意义，配对卡方检验检验配对计数资料的差异是否有统计学意义。

基本思想：

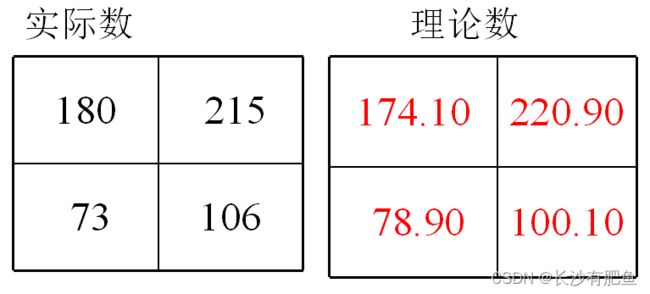
检验实际频数(A)和理论频数(T)的差别是否由抽样误差所引起的。也就是由样本率（或样本构成比）来推断总体率或构成比。

实例：

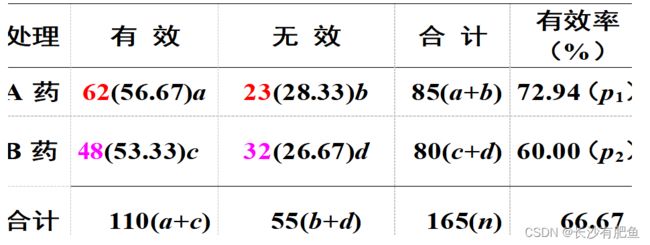
两种药物治疗胃溃疡有效率的比较

理论频数与实际频数的差别:

                       

ARC是位于R行C列交叉处的实际频数， TRC是位于R行C列交叉处的理论频数。 （ ARC - TRC ）反映实际频数与理论频数的差距，除以TRC 为的是考虑相对差距。所以，χ^2 值反映了实际频数与理论频数的吻合程度， χ^2 值大，说明实际频数与理论频数的差距大。 χ^2 值的大小除了与实际频数和理论频数的差的大小有关外，还与它们的行、列数有关。即自由度的大小。

理论频数根据假设来计算的：

无效假设是A药组与B药组的总体有效率相等，均等于合计的阳性率66.67%（110/165）。那么理论上，A药组的85例中阳性人数应为85(110/165)=56.67，阴性人数为85(55/165)=28.33；同理，B药组的80例中阳性人数应为80(110/165)=53.33，阴性人数为80(55/165)=26.67。

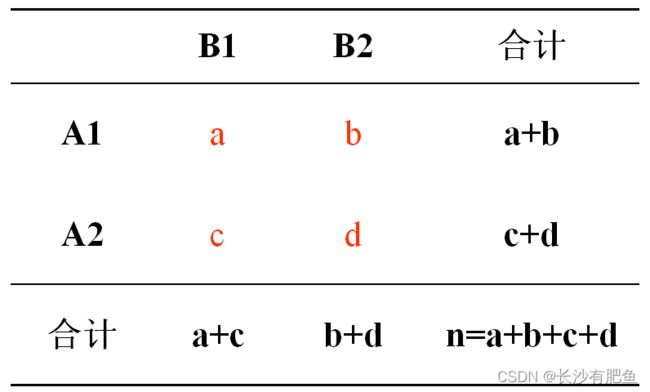
一般的四格表：

 

 若检验假设H0:π1=π2成立，四个格子的实际频数A 与理论频数T 相差不应该很大，即统计量χ2 不应该很大。如果χ2 值很大，即相对应的P 值很小，若 P≤α，则反过来推断A与T相差太大，超出了抽样误差允许的范围，从而怀疑H0的正确性，继而拒绝H0，接受其对立假设H1，即π1≠π2 。

实例：

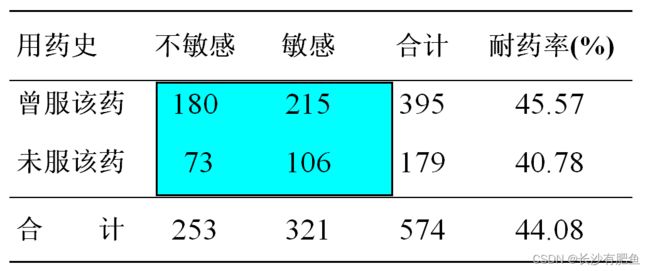
某药品检验所随机抽取574名成年人，研究抗生素的耐药性（资料如表8-11）。问两种人群的耐药率是否一致？

 

（1）建立假设并确定检验水准

• H0:两种人群对该抗生素的耐药率相同，即π1 = π2; （两总体率相等）
• H1:两种人群对该抗生素的耐药率不同，即π1≠π2 ；（两总体不相等）
• a=0.05

（2）计算检验统计量

（3）得出结果

查表确定P值， P＞0.05，得出结论。按0.05水准，不拒绝H0,可以认为两组人群对该抗生素的耐药率的差异无统计学意义。

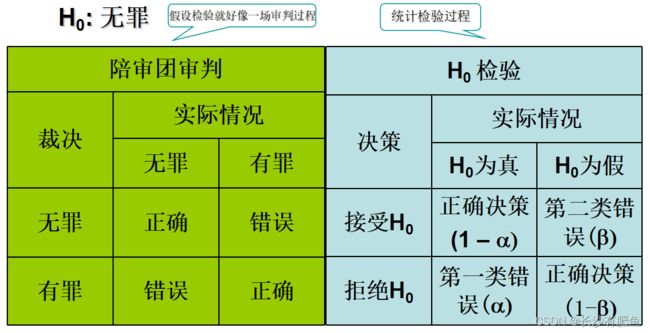
 假设检验中的两类错误

第一类错误（弃真错误）：

• 原假设为真时拒绝原假设
• 第一类错误的概率为α

第二类错误（取伪错误）：

• 原假设为假时接受原假设
• 第二类错误的概率为β

 

实例：

一个公司有员工3000 人（研究的总体） ，为了检验公司员工工资统计报表的真实性，研究者作了 50 人的大样本随机抽样调查，人均收入的调查结果是： X （样本均值）=871 元；S（标准差）=21 元 问能否认为统计报表中人均收入μ0=880 元的数据是真实的？（显著性水平α=0.05 ）

• 原假设 H0：调查数据 871 元与报表数据 880 元之间没有显著性差异，公司员工工资均值的真实情况为880 元；
• 假设 H1：调查数据和报表数据之间有显著性的差异，公司员工工资均值的真实情况不是880 元。

α 错误出现原因：

我们只抽了一个样本，而个别的样本可能是特殊的，不管你的抽样多么符合科学抽样的要求。理论上讲，在 3000 个员工中随机抽取 50 人作为调查样本，有很多种构成样本的可能性，相当于 3000 选 50，这个数目是很大的。这样，在理论上就有存在很多个样本平均数。也就是说，由于小概率事件的出现，我们把本来真实的原假设拒绝了。这就是 α 错误出现的原因。

β 错误出现原因：

第二个问题是，统计检验的逻辑犯了从结论推断前提的错误。命题 B 是由命题 A 经演绎推论出来的，或写作符号 A→B，命题 C 是我们在检验中所依据操作法则。如果A 是真的，且我们从 A 到 B 的演绎推论如果也是正确的，那么B 可能是真实的。相反，如果结果 B是真实的，那么就不能得出A 必定是真实的结论。这就是 β错误出现的原因。

α 错误概率计算：

由实际推断原理引起的，即“小概率事件不会发生”的假定所引起的，所以有理由将所有小概率事件发生的概率之和或者即显著性水平（α=0.05）看作α错误发生的概率，换言之，α错误发生的概率为检验所选择的显著性水平。如果是单侧检验，弃真错误的概率则为 α/2。

β错误的概率计算：

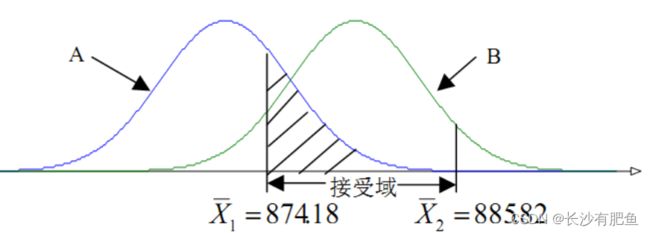
犯β错误的概率的计算是比较复杂的，由于β错误的出现原因是属于逻辑上的，所以在总体参数不知道的情况下是无法计算它出现概率的大小的。 我们在以上例子的基础上进一步设计：这个公司职员的实际工资不是880 元，而是是 870 元，原假设为伪，仍然假设实际工资是880元。这样我们就可以在总体均值为 870 元和 880元两种情况下， 分别作出两条正态分布曲线 （A线和 B 线）

犯 β错误的概率大小就是相对正态曲线A 而言，图 1 中阴影部分的面积： ZX1=1.41 ；ZX2=5.59
查标准正态分布表可知，β=Φ（ZX2）-Φ（ZX1）=0.0793 结果表明，如果总体的真值为 870 元，而虚无假设为880元的话，那么，平均而言每100 次抽样中，将约有8次把真实情况当作880 元被接受，即犯β错误的概率大小是0.0793。

犯第一类错误的危害较大，由于报告了本来不存在的现象，则因此现象而衍生出的后续研究、应用的危害将是不可估量的。想对而言，第二类错误的危害则相对较小，因为研究者如果对自己的假设很有信心，可能会重新设计实验，再次来过，直到得到自己满意的结果（但是如果对本就错误的观点坚持的话，可能会演变成第一类错误）。