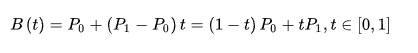Unity 贝塞尔曲线(Beizer curve)的原理与运用
前言:现在使用各种搜索引擎 搜索贝塞尔曲线,都会有很多介绍。这里自己写一篇博客,只是记录一下自己的学习过程与运用方法,方便后续回忆。
贝塞尔曲线原理
1、一阶贝塞尔曲线:
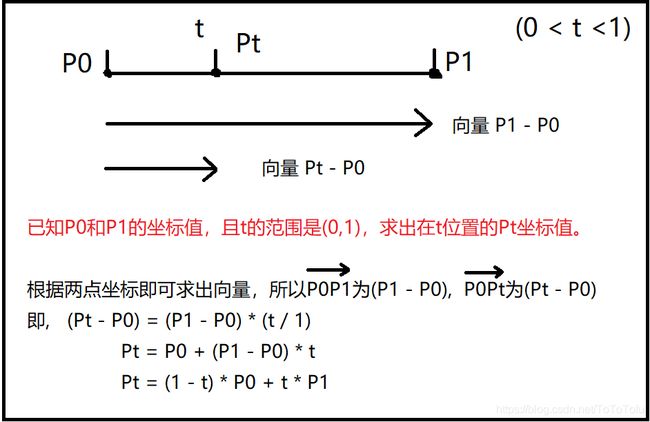
一阶贝塞尔曲线,其实就是找一根线中的其中一点。通过把这些点集合连接,就是一阶贝塞尔曲线(也是当前的线段)。
先来个标准公式 :
上述公式中,B(t)为t时间下点的坐标 求和
然后随便画个推导:
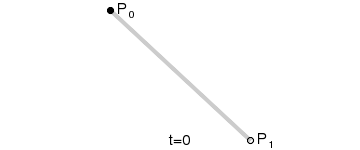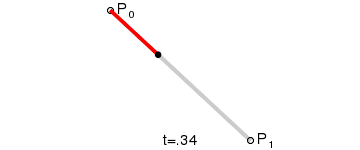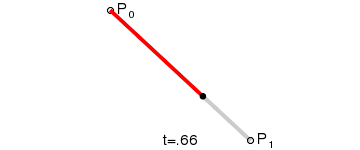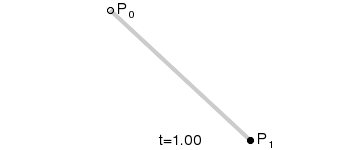
网上找到的示例图GIF:
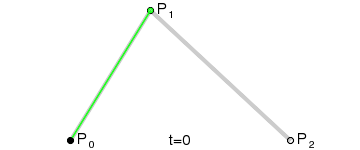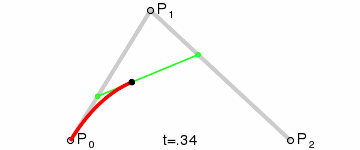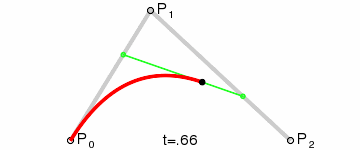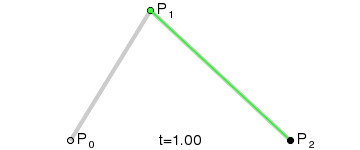
2、二阶贝塞尔曲线:
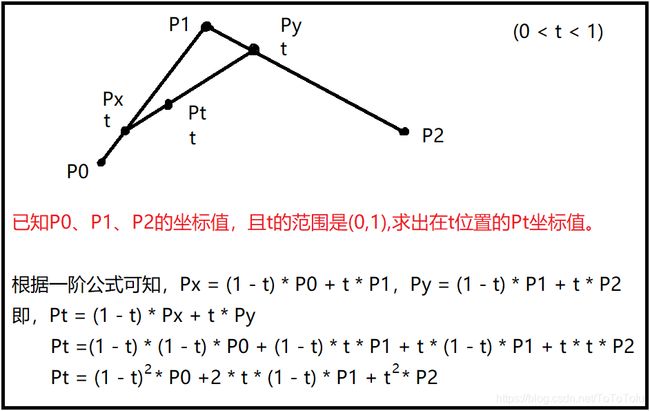
二阶贝塞尔曲线,就是先在所知的相连的两个点之间找出对应点,然后再把这两个点连线,找出最终的点。
通过把找出来的点集合,连线,就是二阶贝塞尔曲线。(点集合越多,曲线越精细,后面C#代码有体现)
先来个标准公式:
上述公式中,B(t)为t时间下点的坐标 求和
然后随便画个推导:
网上找到的示例图GIF:
上图中,P0为起点,Pn为终点,Pi为控制点
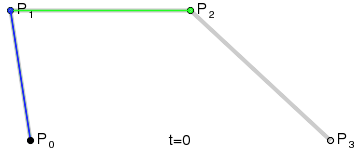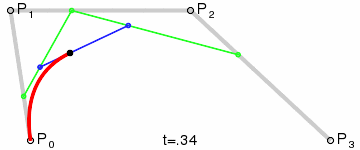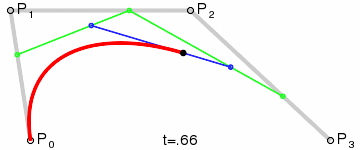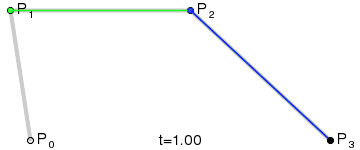
3、三阶贝塞尔曲线:
原理跟上面的二阶贝塞尔曲线类似,只是多了一重。(点集合越多,曲线越精细,后面C#代码有体现)
先来个标准公式:
上述公式中,B(t)为t时间下点的坐标 求和
然后随便画个推导:
网上找到的示例图GIF:
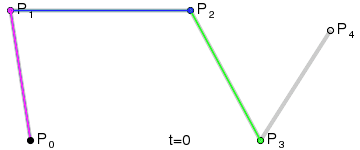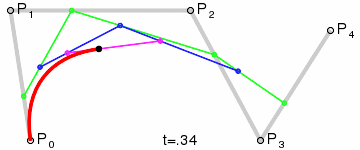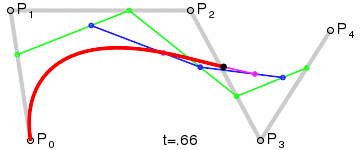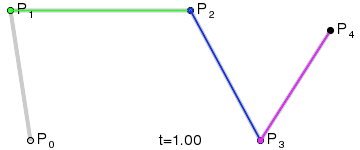
4、多阶贝塞尔曲线:
最终公式:
上述公式中,B(t)为t时间下点的坐标 求和
四阶贝塞尔曲线示例图GIF:
五阶贝塞尔曲线示例图GIF:
贝塞尔曲线运用
1、直接上核心代码.
// 一阶贝塞尔曲线,参数P0、P1、t对应上方原理内的一阶曲线参数.
Vector3 Bezier(Vector3 p0, Vector3 p1, float t)
{
return (1 - t) * p0 + t * p1;
}
// 二阶贝塞尔曲线,参数对应上方原理内的二阶曲线参数.
Vector3 Bezier(Vector3 p0, Vector3 p1, Vector3 p2, float t)
{
Vector3 p0p1 = (1 - t) * p0 + t * p1;
Vector3 p1p2 = (1 - t) * p1 + t * p2;
Vector3 temp = (1 - t) * p0p1 + t * p1p2;
return temp;
}
// 三阶贝塞尔曲线,参数对应上方原理内的三阶曲线参数.
Vector3 Bezier(Vector3 p0, Vector3 p1, Vector3 p2, Vector3 p3, float t)
{
Vector3 temp;
Vector3 p0p1 = (1 - t) * p0 + t * p1;
Vector3 p1p2 = (1 - t) * p1 + t * p2;
Vector3 p2p3 = (1 - t) * p2 + t * p3;
Vector3 p0p1p2 = (1 - t) * p0p1 + t * p1p2;
Vector3 p1p2p3 = (1 - t) * p1p2 + t * p2p3;
temp = (1 - t) * p0p1p2 + t * p1p2p3;
return temp;
}
// 多阶贝塞尔曲线,使用递归实现.
public Vector3 Bezier(float t, List<Vector3> p)
{
if (p.Count < 2)
return p[0];
List<Vector3> newp = new List<Vector3>();
for (int i = 0; i < p.Count - 1; i++)
{
Debug.DrawLine(p[i], p[i + 1]);
Vector3 p0p1 = (1 - t) * p[i] + t * p[i + 1];
newp.Add(p0p1);
}
return Bezier(t, newp);
}
2、Unity案例.
使用LineRenderer来绘制线,Emmm…比较简单,还是直接上代码吧.
using System.Collections;
using System.Collections.Generic;
using UnityEngine;
/// 根据插值,得到的曲线最终点
private Vector3 BezierMethod(float t, List<Vector3> foceList)
{
if (foceList.Count < 2)
return foceList[0];
List<Vector3> temp = new List<Vector3>();
for (int i = 0; i < foceList.Count - 1; i++)
{
Debug.DrawLine(foceList[i], foceList[i + 1], Color.yellow);
Vector3 proportion = (1 - t) * foceList[i] + t * foceList[i + 1];
temp.Add(proportion);
}
return BezierMethod(t, temp);
}
}
运行截图:
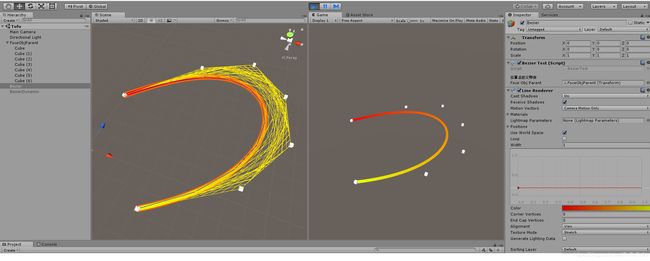
上方的代码是固定不动的贝塞尔曲线,要想动态,只需要稍作改动,Emmm…直接看下面代码吧.
using System.Collections;
using System.Collections.Generic;
using UnityEngine;
/// 根据插值,得到的曲线最终点
private Vector3 BezierMethod(float t, List<Vector3> foceList)
{
if (foceList.Count < 2)
return foceList[0];
List<Vector3> temp = new List<Vector3>();
for (int i = 0; i < foceList.Count - 1; i++)
{
Debug.DrawLine(foceList[i], foceList[i + 1], Color.yellow);
Vector3 proportion = (1 - t) * foceList[i] + t * foceList[i + 1];
temp.Add(proportion);
}
return BezierMethod(t, temp);
}
}
再来张动态贝塞尔曲线的截图,拖动Cube物体,可以动态改变贝塞尔曲线.
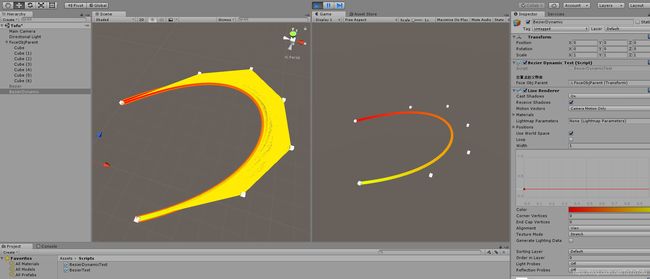
完毕.
ref:
公式
GIF示例图
markdown文本显示emoji表情