Conv1d 计算与b格应用心得
网上找不到一篇讲的比较好的中文稿件。只好自己动手了。
最后附带了个人心得。
下述代码为torch 1.0版本实现。
目录
一、基本运算介绍
二、一个简单版本的一维卷积
1.定义input
2.定义filter
3.做一维卷积运算
4.代码实现
三、一个扩展的一维卷积示例
四、其他话
①有些文章把kernel_size=len_seq时的1-d conv称为full connected
②反过来!就很妙了!提升san值好手法!
一、基本运算介绍
一维卷积,有3个核心参数。
torch.nn.Conv1d(in_channel,out_channel,kernel_size)
宏观地说,传入一个(N,C_in,L)的input,输出一个(N,C_out,移动次数)的张量。
其中,L就是序列的长度。
移动次数= (Len_seq-kernel_size+1)/stride,可以稍后再结合图像理解。
二、一个简单版本的一维卷积
先来看一个最简单的版本。
1.定义input
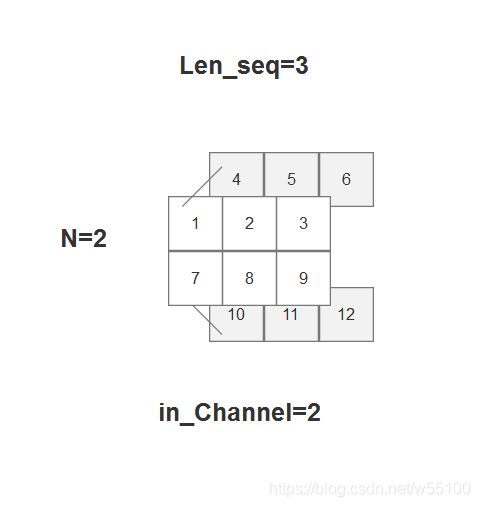
输入一个batch=2,每一个batch内的句子长度len=3的数据,in_channel=2。
在上图中,第1个batch内,就是 [[1,2,3],[4,5,6]] 这个(C_in,len_seq)形状的张量。
2.定义filter
fliter的形状是(C_in,kernel_size)。
为了便于观察和说明,我们约定一个特殊的参数矩阵。
3.做一维卷积运算
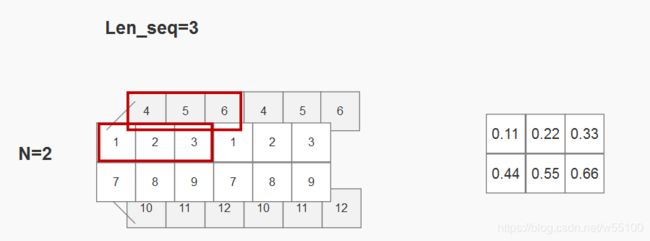
具体过程如下图
我们拆解一下
(1)计算batch=1
为了便于理解,我把filter的参数矩阵重新排列了一下。
如果不理解什么是卷积,那么这就是卷积,2个二维张量卷积之后变成一维。
(2)同理,计算batch=2
(3)拼接不同batch的结果,就是当前filter的输出,这就回到了最开始的图。
现在看起来更直观了
(4)拼接C_out个filter的结果,得到output
在(3)中,一个(C_in,kernel_size)的filter,得到一个(batchsize,滑动次数)的feature map。
本例中,滑动次数=1,所以得到形状(2,1)的张量。
由于我们设置了C_out个张量,所以最终会得到(batchsize,C_out,滑动次数)的output。
注意为了保持与输入(N,C,L)一致性,这里C_out被移动到中间。
这就是一个最简单的1维卷积了。
核心是记住filter =(C_in,kernel_size)。
在每一个输入的通道上,都有长为kernel_size的权重,去做一次内积运算,得到一个数值。
4.代码实现
import torch
"""
设计input
"""
inp = torch.Tensor( [1,2,3,4,5,6,7,8,9,10,11,12]).view(2,2,3)
#print(inp)
#tensor([[[ 1., 2., 3.],
[ 4., 5., 6.]],
[[ 7., 8., 9.],
[10., 11., 12.]]])
#inp.shape=[2,2,3] = (batchsize,C_in,Len_seq)
#如同上文定义的一样
"""
设计参数矩阵
"""
a=torch.nn.Conv1d(in_channels=2,out_channels=3,kernel_size=3,bias=False)
myw = torch.FloatTensor([[0.11,0.22,0.33],[0.44,0.55,0.66]]).expand(3,2,3)
a.weight= torch.nn.Parameter(myw)
#print(a.weight)
#Parameter containing:
tensor([[[0.1100, 0.2200, 0.3300],
[0.4400, 0.5500, 0.6600]],
[[0.1100, 0.2200, 0.3300],
[0.4400, 0.5500, 0.6600]],
[[0.1100, 0.2200, 0.3300],
[0.4400, 0.5500, 0.6600]]], requires_grad=True)
#记得,参数矩阵的形状是(C_out,C_in,kernel_size)
#这里为了简化,我让3个(即C_out个)filter的参数完全一致。
"""
计算输出
"""
out = a(inp)
#print(out)
#tensor([[[10.0100],
[10.0100],
[10.0100]],
[[23.8700],
[23.8700],
[23.8700]]], grad_fn=)
#10.01和23.87,与我们计算的完全一致
三、一个扩展的一维卷积示例
再来理解一下什么是滑动次数。
这次我们输入一个长度len_seq=6的数据,kernel_size仍然保持3,stride=1。
理论上,对每一个filter我们将得到(batchsize,滑动次数=2)的结果。
import torch
inp = torch.Tensor( [1,2,3,4,5,6,7,8,9,10,11,12]).view(2,2,3)
inp=inp.repeat(1,1,2)
#print(inp)
#tensor([[[ 1., 2., 3., 1., 2., 3.],
[ 4., 5., 6., 4., 5., 6.]],
[[ 7., 8., 9., 7., 8., 9.],
[10., 11., 12., 10., 11., 12.]]])
a=torch.nn.Conv1d(in_channels=2,out_channels=3,kernel_size=3,stride=2,bias=False)
myw = torch.FloatTensor([[0.11,0.22,0.33],[0.44,0.55,0.66]]).expand(3,2,3)
a.weight= torch.nn.Parameter(myw)
out=a(inp)
#out.shape
#torch.Size([2, 3, 2])
#可以看到不再是[2,3,1]了
#print(out)
#tensor([[[10.0100, 9.3500],
[10.0100, 9.3500],
[10.0100, 9.3500]],
[[23.8700, 23.2100],
[23.8700, 23.2100],
[23.8700, 23.2100]]], grad_fn=) 用图像理解就是
kernel_size=3,所以滑动窗口大小为3,第一次是这样。
由于stride=2,第二次是这样。
验算也可以证明,确实得到的是9.35=3*0.11+1*0.22+2*0.33+6*0.44+4*0.55+5*0.66。
四、其他话
最近看的一些论文都有提到,把他们自己论文里提出的各种奇怪的张量运算,称为variant of 1-d convolution。
如果不理解Conv1d,去看这些文章,就不能理解作者写这句话是表达了什么视角。
故撰此文以自省。
①有些文章把kernel_size=len_seq时的1-d conv称为full connected
如果看成矩阵形式并不好理解。
所以应该这样,对每一个batch,(c_in,len_seq)的数据,flatten成 (c_in*lenseq)的数据。
然后输入一个Linear(c_in*len_seq,1)的全连接层,得到一个具体的数值。
这样一来,确实等价于全连接。
【注:如果kernel_size不等于len_seq就不一样了,因为还有一个滑动的概念。】
②反过来!就很妙了!提升san值好手法!
既然在①中,证明了【kernel_size=len_seq时】的1-d conv 等价于FC。
那么!为什么不能反过来说FC等价于1-d conv呢???
对吧,你在论文里,如果写,此处我们将vector展平,然后接上一个to (1)的fc layer。
这多low啊!多掉san值啊!
要写就这样写。
so far 我们得到了一组(N,M,C)数据。
inspired by CNN in graph tasks,我们将C视为通道数,那么我们的算法其实等价于variant of 1-d convolution。
尤其是非图像领域的论文,这样一写,b格瞬间就不一样了。
如果觉得san值还不够,可以学费马那样,再补一句。
We omit the detailed proof due to space limitation.
费马他老人家也总是在书边缘留白处写,啊这个我已经证明了,但空间有限就不写了。
③更特殊的情况,filters share weights among channels
就是在任何一个channel层面,filter的参数是相同的。
这个又可以应用于很多3维的数据。假设我们还是(N,M,C),C是一个非特异的维度。
想不到很好的例子。。。
比如说是性别吧,C=2,区分male和female的数据。
由于女权主义者的存在,我们需要保证在C方向上,所有filter的参数都是一样的。
即处理channel=male,和处理channel=female时,必须一视同仁。
这在某些场景下是很有道理的,甚至你不这么做会有生命危险(狗头)。
然后我们又可以写,这其实也是variant of 1-d conv!只不过share weights among channels。
总结一下。
我在此提出我的猜想。
对所有3维数据(N,M,C),如果只在其中2个维度上进行矩阵点乘,然后降维求和,那么都可以往conv1d上凑。
---220227 update---
特别地,对1x1的conv1d,
假设输入是常见的(N,A,B)三维张量。
我们其实有两种选择,来设置A与B何者为channel。
设A为channel时, kernel形状(C_in, k) = (A,1) 。
一个kernel卷完得到(N,B)。
意味着A通道之间有差异,而在B方向上共享参数。