数据结构：二叉树的链式结构及对链式二叉树的一些基本操作

本文总结课上讲到的链式二叉树的一些基本操作，具体有

• 计算二叉树的结点的个数
• 计算二叉树叶子节点的个数
• 计算二叉树第K层结点的个数
• 计算二叉树的深度/高度
• 查找并返回值为x的结点
• 判断二叉树是否是完全二叉树
• 二叉树的销毁
• 二叉树的前、中、后序遍历
• 二叉树的层序遍历

由于二叉树结构特点，以上函数全部都由递归实现，需要熟练使用递归控制二叉树。
还从提了一下广度优先遍历和深度优先遍历的定义。

二叉树的实现之链式结构

结构定义：

typedef char BTDataType;
typedef struct BinaryTreeNode
{
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
	BTDataType data;
}BTNode;

手动创建一个二叉树，放边后面实现对二叉树的操作

BTNode* BuyNode(BTDataType x)
{
	BTNode* node = (BTNode*)malloc(sizeof(BTNode));
	if (node == NULL)
	{
		printf("malloc fail\n");
		exit(-1);
	}
	node->data = x;
	node->left = node->right = NULL;
	return node;
}

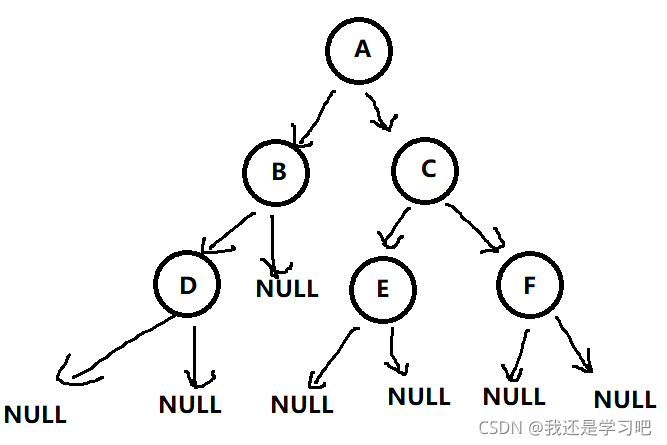
BTNode* CreatBinaryTree()
{
	BTNode* nodeA = BuyNode('A');
	BTNode* nodeB = BuyNode('B');
	BTNode* nodeC = BuyNode('C');
	BTNode* nodeD = BuyNode('D');
	BTNode* nodeE = BuyNode('E');
	BTNode* nodeF = BuyNode('F');
	//BTNode* nodeG = BuyNode('G');

	nodeA->left = nodeB;
	nodeA->right = nodeC;
	nodeB->left = nodeD;
	nodeC->left = nodeE;
	nodeC->right = nodeF;
	//nodeB->right = nodeG;
	return nodeA;
}

二叉树的节点个数

利用返回值实现计数
思想：二叉树节点个数=左子树节点个数+右子树节点个数+1（根节点）

int BinaryTreeSize(BTNode* root)
{
	return root == NULL ? 0 : BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1;
}

使用计数器
由于递归时，不同函数栈帧中的局部变量不是同一个变量，所以要由外部给计数变量，并将它的指针传给函数，使得不同函数修改的是同一个变量。

//如果要用计数器，则应该用参数带回结果
void BinaryTreeSize(BTNode* root, int* pn)
{
	if (root == NULL)
	{
		return;
	}

	++(*pn);
	BinaryTreeSize(root->left, pn);
	BinaryTreeSize(root->right, pn);
}

二叉树叶子节点的个数

//二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root)
{
	if (root == NULL)//可能是整个树是空，也可能子树是空
	{
		return 0;
	}
	//没有左右孩子的节点是叶子节点
	if (root->left == NULL && root->right == NULL)
	{
		return 1;
	}
	return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}

二叉树第K层节点的个数

思想：将问题拆解，第K层节点的个数=左子树第K-1层节点个数+右子树第K-1层节点个数。

int BinaryTreeLeveKSize(BTNode* root, int k)
{
	assert(k >= 1);
	if (root == NULL)
	{
		return 0;
	}
	if (k == 1)
	{
		return 1;
	}
	return BinaryTreeLeveKSize(root->left, k - 1) + BinaryTreeLeveKSize(root->right, k - 1);
}

二叉树的深度/高度

思想：二叉树深度=左子树深度和右子树深度的较大值+1（根节点）
注意这里为了避免重复调用，需要把左子树和右子树深度保存在变量中。

int BinaryTreeDepth(BTNode* root)
{
	if (root == NULL)//空树层数为0
	{
		return 0;
	}
	int leftDepth = BinaryTreeDepth(root->left);
	int rightDepth = BinaryTreeDepth(root->right);

	return leftDepth > rightDepth ? leftDepth + 1 : rightDepth + 1;
}

二叉树查找值为x的节点

要求：返回第一个节点的值与x相等的节点，找不到返回NULL
思想：空树（空子树）直接返回空（当前节点为空直接返回空），若当前节点不为空，且值和x相等，返回当前节点；若当前节点值和x不相等，再看左子树和右子树是否有目标节点。
找到了返回值必不为空，如果在左子树找到了就逐层返回（注意不是一步返回到最外层函数的），不会再查找右子树。

//二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
	if (root == NULL)//处理空树（也可能是递归中遇到的空子树）
	{
		return NULL;
	}
	if (root->data == x)
	{
		return root;
	}
	BTNode* leftRet = BinaryTreeFind(root->left, x);
	if (leftRet)//返回值非空说明找到了，直接返回
	{
		return leftRet;
	}
	BTNode* rightRet = BinaryTreeFind(root->right, x);
	if (rightRet)
	{
		return rightRet;
	}
	return NULL;
}

判断二叉树是否是完全二叉树

这个函数实现思想是由下面的用队列实现层序遍历思想的延申。
把节点进队列的时候，把空指针也进队列。
出队的时候，当遇到空指针，就判断队列中剩下的元素是否由非空节点，如有非空节点，则不是完全二叉树；反之是完全二叉树。

注意要修改队列元素类型为二叉树结点指针类型，因为我把链式二叉树结构的声明和队列实现放在不同文件，所以要前置声明二叉树结点指针类型。

bool BinaryTreeComplete(BTNode* root)
{
	Queue q;
	QueueInit(&q);
	QueuePush(&q, root);
	//先层序遍历，遇到空就停止（完全二叉树遇到空以后，队列后面剩下的元素必定全是NULL，
	//非完全二叉树则不一定，并且遇到空以后可能还有非空元素没有进队列）
	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);
		if (front == NULL)
		{
			break;
		}
		else
		{
			QueuePush(&q, front->left);//空指针也进队列
			QueuePush(&q, front->right);
		}
	}
	//遇到空以后，检查剩下的节点有没有非空
	//1、剩下的全是空，则是完全二叉树
	//2、剩下的存在非空，则不是完全二叉树
	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);
		if (front)
		{
			QueueDestroy(&q);
			return false;
		}
	}
	QueueDestroy(&q);//无头链式队列实际上pop完之后已经把空间全部释放了，
	//但是从不知道队列内部具体实现的使用者来说，逻辑上这里要释放空间避免出现内存泄漏
	return true;
}

二叉树销毁

思想：由于把根节点释放了就找不到孩子节点了，必须从下往上释放，适合用递归实现。
因为传一级指针，所以根指针由使用者在外部指控

void BinaryTreeDestroy(BTNode* root)//调用者置空
{
	if (root == NULL)//空树不必置空（也可能是子树为空，则直接返回上一层）
	{
		return;
	}
	BinaryTreeDestroy(root->left);
	BinaryTreeDestroy(root->right);
	free(root);
}

二叉树的遍历

前序遍历、中序遍历、后序遍历、层序遍历、广度优先遍历、深度优先遍历

定义：

1. 前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点的操作发生在遍历其左右子树之前。
2. 中序遍历(Inorder Traversal)——访问根结点的操作发生在遍历其左右子树之中（间）。
3. 后序遍历(Postorder Traversal)——访问根结点的操作发生在遍历其左右子树之后。

例子：


代码
前序遍历

void PreOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	printf("%c ", root->data);
	PreOrder(root->left);
	PreOrder(root->right);
}

中序遍历

void InOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	InOrder(root->left);
	printf("%c ", root->data);
	InOrder(root->right);
}

后序遍历

void PostOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	PostOrder(root->left);
	PostOrder(root->right);
	printf("%c ", root->data);
}

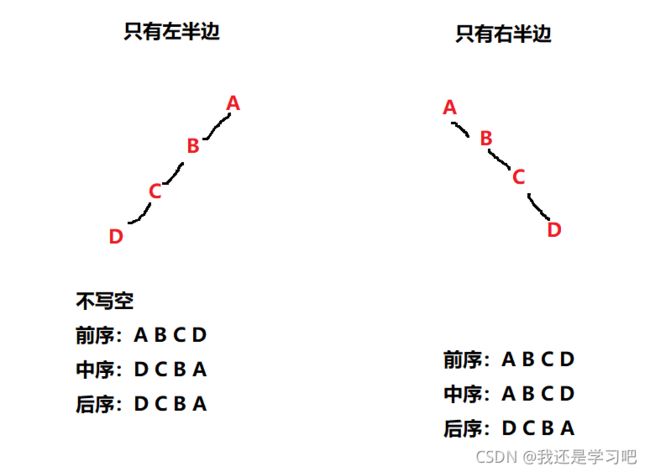
当前序遍历和后序遍历的访问结果正好相反时，说明这是一个单边树
如图所示：

层序遍历定义：
设二叉树的根节点所在层数为1，层序遍历就是从所在二叉树的根节点出发，首先访问第一层的树根节点，然后从左到右访问第二层上的节点，接着是第三层的节点，以此类推，自上而下，自左至右逐层访问树的结点的过程就是层序遍历。
图示

实现思想：
使用队列实现；
先把根节点进队列；
当队列不为空，就把队首元素出队（访问这个结点），并让出队节点的两个孩子进队列（左孩子先进），空指针不进队列。
当队列为空时就实现了层序遍历。

代码

void BinaryTreeLevelOrder(BTNode* root)
{
	if (root == NULL)
	{
		return;
	}
	Queue q;
	QueueInit(&q);
	QueuePush(&q, root);
	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);
		printf("%c ", front->data);

		//孩子带进队列
		if (front->left)
		{
			QueuePush(&q, front->left);
		}

		if (front->right)
		{
			QueuePush(&q, front->right);
		}
	}
	printf("\n");

	QueueDestroy(&q);
}

广度优先遍历定义：把下一步所有可能的位置遍历完才会进行更深层次的遍历。层序遍历就是一种广度优先遍历。

深度优先遍历定义：先遍历完一条完整的路径（从根到叶子节点的完整路径）才会向上层折返，再去遍历下一个路径。前序遍历就是一种深度优先遍历。