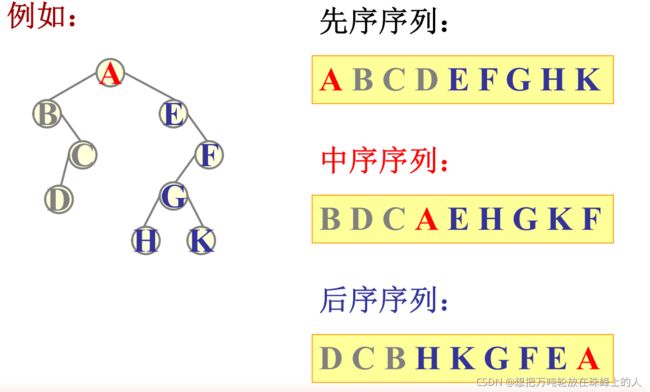
数据结构--C语言实现链式二叉树--详解
文章目录
- 二叉树基本知识
-
- 相关术语
- 二叉树性质
- 二叉树遍历编辑
- 二叉树基本操作
-
- 一、结点定义
-
- 关于结构体名和结构体名是指针的定义区别
- 二、二叉树的创建
-
- 先序序列构造二叉树
- 三、先左后右的递归遍历算法
-
- 1.中序序列遍历二叉树
- 2.先序序列遍历二叉树
- 3.后序序列遍历二叉树
- 四、先左后右的非递归遍历算法
- 五、二叉树的拷贝
- 六、求二叉树的深度(后序遍历)
- 七、删除二叉树中以X为根的子树
- 八、二叉树的删除(二叉搜索树)
- 九、二叉树的插入(二叉搜索树)
二叉树基本知识
二叉树(binary tree)是指树中节点的度不大于2的有序树,它是一种最简单且最重要的树。二叉树的递归定义为:二叉树是一棵空树,或者是一棵由一个根节点和两棵互不相交的,分别称作根的左子树和右子树组成的非空树;左子树和右子树又同样都是二叉树 。
相关术语
①结点:包含一个数据元素及若干指向子树分支的信息 。
②结点的度:一个结点拥有子树的数目称为结点的度 。
③叶子结点:也称为终端结点,没有子树的结点或者度为零的结点 。
④分支结点:也称为非终端结点,度不为零的结点称为非终端结点 。
⑤树的度:树中所有结点的度的最大值 。
⑥结点的层次:从根结点开始,假设根结点为第1层,根结点的子节点为第2层,依此类推,如果某一个结点位于第L层,则其子节点位于第L+1层 。
⑦树的深度:也称为树的高度,树中所有结点的层次最大值称为树的深度。
二叉树性质
性质1:二叉树的第i层上至多有2i-1(i≥1)个节点 。
性质2:深度为h的二叉树中至多含有2h-1个节点 。
性质3:若在任意一棵二叉树中,有n0个叶子节点,有n2个度为2的节点,则必有n0=n2+1 。
性质4:具有n个节点的完全二叉树深为log2x+1(其中x表示不大于n的最大整数) 。
性质5:若对一棵有n个节点的完全二叉树进行顺序编号(1≤i≤n),那么,对于编号为i(i≥1)的节点:
当i=1时,该节点为根,它无双亲节点 。
当i>1时,该节点的双亲节点的编号为i/2 。
若2i≤n,则有编号为2i的左节点,否则没有左节点 。
若2i+1≤n,则有编号为2i+1的右节点,否则没有右节点 。
二叉树遍历编辑
遍历是对树的一种最基本的运算,所谓遍历二叉树,就是按一定的规则和顺序走遍二叉树的所有结点,使每一个结点都被访问一次,而且只被访问一次。
以上内容均来自百度百科
二叉树基本操作
一、结点定义
typedef char DataType;
typedef struct node{
DataType data;
struct node *lchild,*rchild; //指向左右孩子的指针
}BiTNode,*BiTree;
二叉树结点定义依托于结构体,对于结构体有一点想说:
关于结构体名和结构体名是指针的定义区别
typedef struct dot{
int a;
double b;
}node,*point; //重命名两个新的数据类型(结构体)
//后一个一个是指针方式的名字
int main()
{
char c='C';
node A; //emp_i 声明的A是一个实体,声明了就已经有存储空间了
point B; //point 声明的B是一个指针
//但这里不用加*号,因为point已经被指定为指针
//它可以指向一个struct dot的实体。
A.a ++;
B->a ++;
}
必须要弄清这一点,因为在后面的代码我们有时会为了方便用不同的方式来指向结点
二、二叉树的创建
先序序列构造二叉树
先序遍历的顺序为先到根节点,再到左节点,最后到右节点;结点数据类型为字符型,空结点用’#'表示。
void Create(BiTree * T)
{
char word;
scanf("%c",&word);
if(word=='#')
*T=NULL;//对空结点置空处理,若不置空遍历时无法结束
else
{
(*T)=(BiTree)malloc(sizeof(BiTNode));//为每个结点申请空间
//也包括根结点
(*T)->data =word;
Create(&(*T)->lchild );//递归的进行创建
Create(&(*T)->rchild );
}
}
对于用其它两种序列来构造二叉树,此处不做赘述,用什么序列来构造二叉树并不是很重要,因为最后得到的结果都是相同的。
三、先左后右的递归遍历算法
1.先(根)序的遍历算法
若二叉树为空树,则空操作;否则,
(1)访问根结点;
(2)先序遍历左子树;
(3)先序遍历右子树。
2.中(根)序的遍历算法
若二叉树为空树,则空操作;否则,
(1)中序遍历左子树;
(2)访问根结点;
(3)中序遍历右子树。
3.后(根)序的遍历算法
若二叉树为空树,则空操作;否则,
(1)后序遍历左子树;
(2)后序遍历右子树;
(3)访问根结点
1.中序序列遍历二叉树
void IneOrder(BiTree *root)
{
if(*root==NULL)
return ;
InOrder(&(*root)->lchild );
printf("%c",(*root)->data );
InOrder(&(*root)->rchild );
}
2.先序序列遍历二叉树
void PreOrder(BiTree *root)
{
if(*root==NULL)
return ;
printf("%c",(*root)->data );
PreOrder(&(*root)->lchild );
PreOrder(&(*root)->rchild );
}
3.后序序列遍历二叉树
void PostOrder (BiTree *root)
{
if(*root==NULL)
return ;
PostOrder(&(*root)->lchild );
PostOrder(&(*root)->lchild );
printf("%c",(*root)->data );
}
四、先左后右的非递归遍历算法
涉及到了一部分栈的相关用法
#include 五、二叉树的拷贝
后序遍历
BiTNode *GetTreeNode(DataType item,BiTNode *lptr , BiTNode *rptr )
{
if (!(T = (BiTree)malloc(sizeof(BiTNode))))
exit(1);
T-> data = item;
T-> lchild = lptr; T-> rchild = rptr;
return T
}
//生成一个二叉树的结点(其数据域为item,左指针域为lptr,右指针域为rptr)
BiTNode *CopyTree(BiTNode *T) {
if (!T ) return NULL;
if (T->lchild )
newlptr = CopyTree(T->lchild); //复制左子树
else newlptr = NULL;
if (T->rchild )
newrptr = CopyTree(T->rchild); //复制右子树
else newrptr = NULL;
newT = GetTreeNode(T->data, newlptr, newrptr);
return newT;
} // CopyTre
六、求二叉树的深度(后序遍历)
算法基本思想:
从二叉树深度的定义可知,二叉树的深度应为其左、右子树深度的最大值加1。由此,需先分别求得左、右子树的深度,算法中“访问结点”的操作为:求得左、右子树深度的最大值,然后加 1 。
int Depth (BiTree T )
{ // 返回二叉树的深度
if ( !T )
depthval = 0;
else
{
depthLeft = Depth( T->lchild );
depthRight= Depth( T->rchild );
depthval = 1 + (depthLeft > depthRight ?
depthLeft : depthRight);//取两者中的较大者
}
return depthval;
}
七、删除二叉树中以X为根的子树
以X为根的子树被删除,故不用考虑其有没有子树。
void Release(BiTree &T)
{
if(T!=NULL){
Release(T->lchild );
Release(T->rchild );
free(T);
T=NULL;
}
}
void Delete(BiTree &T,char X)
{
if(T==NULL)
return ;
if(T->data ==X)
Release(T);
if(T!=NULL){
Delete(T->lchild ,X);
Delete(T->rchild ,X);
}
}
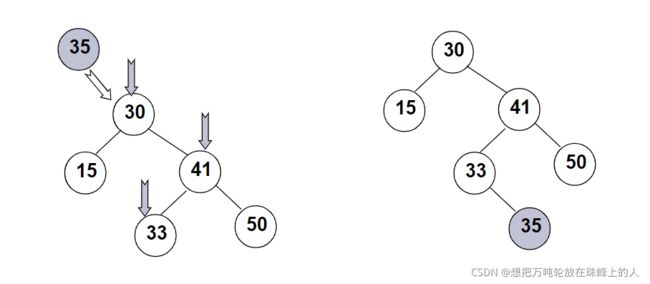
八、二叉树的删除(二叉搜索树)
有三种情况:
1. 删除的结点为叶子结点:直接删除,并再修改其父结点指针为空
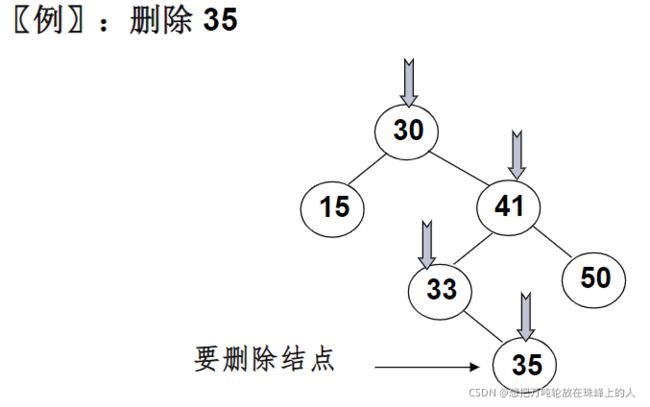
2. 要删除的结点只有一个孩子结点:将其父结点的指针指向要删除结点的孩子结点

3. 要删除的结点有左右两棵子树:用另一结点代替被删除结点:右子树 的最小元素或者左子树的最大元素(通常的树的结点间没有大小关系,但在二叉搜索树中要求对一个结点A,其左子树结点都小于A,右子树的结点都大于A故此情况针对二叉搜索树)
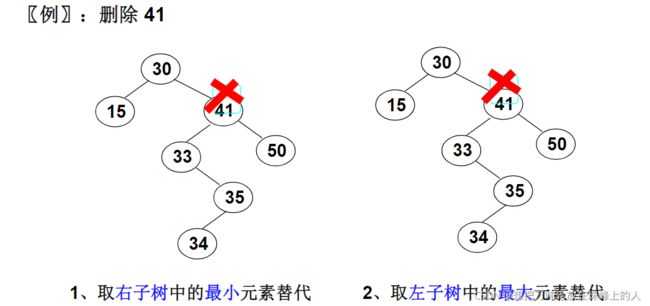
BiTree Delete(BiTree BST, DataType X )
{
BiTree Tmp;
if( !BST )
printf("要删除的元素未找到");
else {
if( X < BST->data )
BST->lchild = Delete( BST->lchild, X );//从左子树递归删除
else if( X > BST->data )
BST->rchild = Delete( BST->rchild, X );//从右子树递归删除
else
{ /* BST就是要删除的结点 */
/* 如果被删除结点有左右两个子结点 */
if( BST->lchild && BST->rchild )
{
/* 从右子树中找最小的元素填充删除结点 */
Tmp = FindMin( BST->rchild );
BST->data = Tmp->data;
/* 从右子树中删除最小元素 */
BST->rchild = Delete( BST->rchild, BST->data );
}
else
{ /* 被删除结点有一个或无子结点 */
Tmp = BST;
if( !BST->lchild ) /* 只有右孩子或无子结点 */
BST = BST->rchild;
else /* 只有左孩子 */
BST = BST->lchild;
free( Tmp );
}
}
}
return BST;
}
九、二叉树的插入(二叉搜索树)
BiTree Insert( BiTree BST, DataType X )
{
if( !BST ){ /* 若原树为空,生成并返回一个结点的二叉搜索树 */
BST = (BiTree)malloc(sizeof(BiTNode));
BST->data = X;
BST->lchild = BST->rchild = NULL;
}
else { /* 开始找要插入元素的位置 */
if( X < BST->data )
BST->lchild = Insert( BST->lchild, X ); /*递归插入左子树*/
else if( X > BST->data )
BST->rchild = Insert( BST->rchild, X ); /*递归插入右子树*/
/* else X已经存在,什么都不做 */
}
return BST;
}