ELMo,GPT, Bert, XLNet 预训练模型对比
Context Based预训练编码器
- 1:自回归语言模型(Decoder-AutoRegression)
-
- ELMo
-
- ELMo简介
- ELMo的缺点
- GPT
-
- GPT简介
- GPT的缺点:
- 2:自编码语言模型(Encoder-AutoEncoding)
-
- BERT
-
- Bert的Pretrain:
- Bert的Fine-tuning
- BERT的缺点:
- 3:排列语言模型(Encoder-AutoEncoding)
-
- XLNet
-
- XLNet的构思
- 待研究的部分
- 实验
与预训练编码器对应的是word2vec,glove等浅层词嵌入,这类浅层词嵌入特点是学习到一个上下文独立的静态词向量。而对于“一词多义”这种现象,它们只能得到这个词在多种不同语境下的一个综合的表达,而当一个新的句子进来时,它是无法给出适配当下语境的词向量的。而预训练编码器则可以得到“上下文相关的词向量”,解决了“一词多义”的问题。
预训练编码器根据优化目标的不同可以分为三种情况:
1:自回归语言模型(Decoder-AutoRegression)
这一类模型是以构建一个语言模型为优化目标,也就是
P ( s ) = ∏ i P ( x i ∣ x 1 , ⋯ , x i − 1 ) P(s) = \prod_i P(x_i|x_1,\cdots,x_{i-1}) P(s)=∏iP(xi∣x1,⋯,xi−1)
- 优点:语言模型联合概率的无偏估计,天然适合自然语言中的生成任务
- 缺点:无法获取双向上下文信息表征
ELMo
Paper:https://arxiv.org/pdf/1802.05365.pdf
ELMo简介
上图为ELMo的训练示意图,由两个单向的三层LSTM语言模型拼接而成,其中 T i = { h i → ∣ ∣ h i ← } T_i = \{\mathop{h_i} \limits ^{\rightarrow}||\mathop{h_i} \limits ^{\leftarrow}\} Ti={hi→∣∣hi←}, h i → \mathop{h_i} \limits ^{\rightarrow} hi→和 h i ← \mathop{h_i} \limits ^{\leftarrow} hi←分别表示从左到右和从右到左训练的两个语言模型的隐层输出。因此ELMo的目标函数是: ∑ i { l o g P ( x i ∣ x 1 , ⋯ , x i − 1 ; Θ → ) + l o g P ( x i ∣ x i + 1 , ⋯ , x N ; Θ ← ) } \sum_i\{log P(x_i|x_1,\cdots,x_{i-1};\mathop{\Theta} \limits ^{\rightarrow}) + log P(x_i|x_{i+1},\cdots,x_{N};\mathop{\Theta} \limits ^{\leftarrow})\} i∑{logP(xi∣x1,⋯,xi−1;Θ→)+logP(xi∣xi+1,⋯,xN;Θ←)}
即同时优化两个单向语言模型。因此其实ELMo通过这种方式一定程度上改善了语言模型无法同时获取上下文信息的缺陷。
ELMo还介绍了如何将训练好的语言模型用于下游NLP任务中。如上图所示,受图像领域预训练模型的启发,作者认为NLP的预训练模型也是越底层学到的特征越是通用领域都会用到的特征,例如单词特征,而越往上学习到的特征就越与训练数据相关,例如句法特征,语义特征。对于上述训练好的预训练模型,每一个输入 x i x_i xi都会对应词编码 E i E_i Ei,两层的从左到右语言模型的隐层输出 h i 1 → , h i 2 → \mathop{h_i^1} \limits ^{\rightarrow}, \mathop{h_i^2} \limits ^{\rightarrow} hi1→,hi2→,以及两层的从右到左语言模型的隐层输出 h i 1 ← , h i 2 ← \mathop{h_i^1} \limits ^{\leftarrow}, \mathop{h_i^2} \limits ^{\leftarrow} hi1←,hi2←,给所有这些向量都配上一个权重,然后就得到一个 x i x_i xi的新的词向量 x i ^ = α i 1 E i + α i 2 h i 1 → + α i 3 h i 2 → + α i 4 h i 1 ← + α i 5 h i 2 ← \hat{x_i} = \alpha_{i1}E_i+\alpha_{i2}\mathop{h_i^1} \limits ^{\rightarrow}+\alpha_{i3}\mathop{h_i^2} \limits ^{\rightarrow}+\alpha_{i4}\mathop{h_i^1} \limits ^{\leftarrow}+\alpha_{i5}\mathop{h_i^2} \limits ^{\leftarrow} xi^=αi1Ei+αi2hi1→+αi3hi2→+αi4hi1←+αi5hi2←
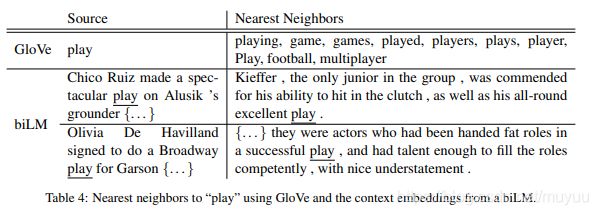
下游任务的任意输入 X X X中的每一个词 x i x_i xi都做同样的处理,就可以得到所有词的词向量表达。固定预训练模型的参数不变,我们只根据下游任务来更新参数 α \alpha α,那么假设句子长度为 N N N,就有 2 N + 1 2N+1 2N+1个参数。通过更新这些参数,同一个词不同语义就可以得到不同的词表达。
上述是一个例子,play这个词在“运动,音乐”两个领域有不同意思。而Glove找出的近邻大多集中在体育领域,可能是因为训练集中体育方面的数据占优势;而ELMo可以根据输入数据的不同,找到与它意思相同的语句。
ELMo的缺点
(与后面的GPT和BERT等比较):
- LSTM抽取特征的能力远弱于Transformer
- 拼接方式的双向融合不如Masked来的好
GPT
Paper: https://www.cs.ubc.ca/~amuham01/LING530/papers/radford2018improving.pdf
GPT简介
GPT的模型实际就是Transfomer模型的Decoder部分,只不过需要去掉 encoder-decoder attention的部分。为什么GPT没有像BERT等模型一样使用Transformer的Encoder部分呢,因为GPT的优化目标也是一个语言模型,而语言模型只能接受从左往右(or从右往左)的输入,否则就不符合语言模型的公式了。当然这种单向的模型会限制GPT在更多应用场景的效果,比如阅读理解,序列标注等任务,因为这类型任务在训练时是可以看到上下文的,而作为预训练模型的GPT却只能看到上文,无法看到下文,势必是会有影响的。
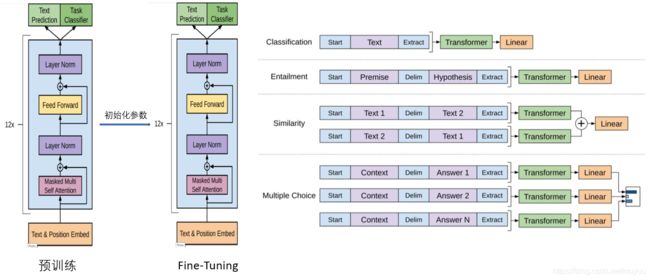
与ELMo不同,GPT在用到下游任务时,是不允许自定义模型结构的,需要跟GPT的结构一致。然后直接利用训练好的GPT模型初始化Fine-Tuning模型的参数,然后再用下游任务的训练数据去训练这个Fine-Tuning模型。
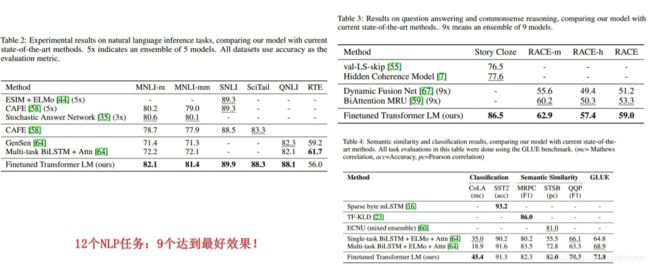
上图是一个针对不同任务如何改造模型结构,使得尽量靠近GPT的网络结构。例如对于分类问题,只需要加上一个起始和终结的符号即可;而对于句子关系判断问题,两个句子间再加分隔号即可;文本相似性判断,把两个句子顺序颠倒做出两个输出即可,这是为了告诉模型句子的顺序不重要;对于多项选择问题,可以给出多路的文章+答案的输入,最后Linear+softmax给出每一路的概率即可。
GPT的缺点:
- 只采用了单向语言模型,不能同时看到上下文,在某些语义理解任务上效果偏弱
2:自编码语言模型(Encoder-AutoEncoding)
与上述自回归模型不同,这类模型的优化目标不是标准的语言模型,而是语言模型的一个有偏估计:
P ( s ) ≈ ∑ i m i l o g P ( x i ∣ x ~ ) P(s) \approx \sum_i m_i logP(x_i|\widetilde{x}) P(s)≈i∑milogP(xi∣x )
- 优点:通过引入噪声构建Masked Language Model,可以获取双向上下文特征。只有被预测的token的权重 m i m_i mi是1,其他都为0。
- 缺点:是语言模型的有偏估计,没有考虑到相邻token直接的相关性,不利于做生成类任务;预训练时的「MASK」噪声在finetune阶段不会出现,造成两阶段不匹配问题。
BERT
Paper:https://arxiv.org/pdf/1810.04805.pdf
BERT与GPT一样,也是分为Pretrain+Fine-Tuning两个阶段。
Bert的Pretrain:
BERT的Pretrain阶段选择了Transfomer模型的Encoder部分,从而可以获取双向上下文特征。但是单纯的使用Transfomer Encoder模型带来的问题是,由于所有的位置都以距离1产生联系,因此当层数足够深,预测某一位置词的时候,是可以“看到”这个词本身的,为了解决这个问题,BERT创造性得引入了Mask方式,将要预测的词用[Mask]代替,不就看不到这个词了吗。
然而这样又会带来另一个问题,就是上面说的“预训练时的「MASK」噪声在finetune阶段不会出现,造成两阶段不匹配问题”。对此BERT的解决方式是:对于一个要被盖住的词,
- 有80%的概率用“[mask]”标记来替换
- 有10%的概率用随机采样的一个单词来替换
- 有10%的概率不做替换(虽然不做替换,但是还是要预测哈)
再加上在前向的时候,模型并不知道最后要预测的是哪些词,所以只能对对所有词都走一遍流程。通过这种方式尽可能的调解模型忽略[Mask]的影响。
Bert的Fine-tuning
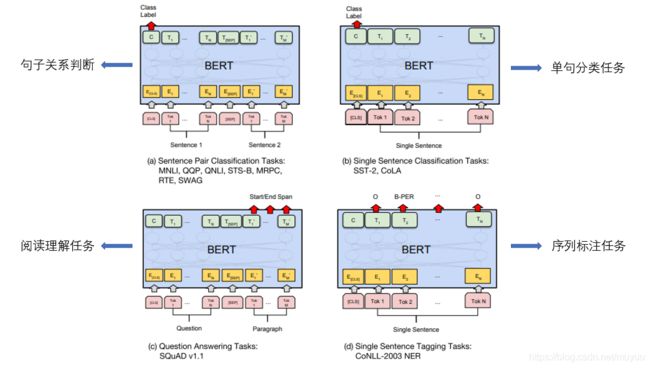
与GPT一样,BERT也要求下游任务的结构与BERT一致,然后利用训练好的预训练模型来初始化下游任务模型的参数。
BERT的输入数据最前面总有一个起始符[CLS],在句子关系判断和单句分类任务中,其他结构都与GPT中介绍的构造方法一样,只不过最终的判断值/类别是通过这个起始符[CLS]串接softmax来得到的;而在阅读理解和序列标注任务中,就只需要将每个token对应的输出进行分类即可。
BERT的缺点:
- BERT实际上是优化了一个以上下文信息为输入的分类问题,而不是像ELMo和GPT一样优化的是传统语言模型,因此它在生成类任务上效果是不如理解类任务的。
- 尽管BERT通过一定的方式改善了由于引入[Mask]导致的pretrain与finetue阶段不匹配的问题,但并不是完全解决了这个问题
- 被maksed掉的词,它们使用的上下文信息都是一样的,唯一的区别就是位置编码p;而随着网络层数加深,位置编码p的信息也容易被过多的计算操作抹去(类似于RNN模型难以建模长距离依赖)
之后的很多模型都是基于BERT进行改进,比如:RoBerta,MASS,UNILM,ENRIE等等…
3:排列语言模型(Encoder-AutoEncoding)
从上面可以看出,基于LM和基于DAE的预训练模型各有千秋,都有优势和劣势。前者的优点是天然适合生成类任务,而且可以显式地获得token直接的依赖关系,但缺点是只能看到一个方向的context;而后者的优势是可以同时编码上下文信息,但其引入的[Mask]机制又导致了pretrain与finetune阶段不匹配的问题,同时也忽略了被mask的词直接的联系。
那么一个很自然的想法就是能不能设计一种模型,使得既可以利用LM模型从左到右的生成方式,但又可以同时编码到上下文信息(ELMo的拼接方式太浅了,不够“深入”)。普通的双向模型是不行的,因为若干层之后,就可以在当前位置“看”到这个词本身(BERT正是由于这个原因才引入了[Mask]),所以关键问题就变成了:如何在同时“看”到上文和下文的情况下,不“看”到自己。这就是研究排列语言模型的动机,典型的例子是XLNet。
XLNet
Paper: https://arxiv.org/pdf/1906.08237.pdf
XLNet的构思
考虑一个例句:
[“我1”,“今天2”,“很3”,“开心4”,“<逗号>5”,“因为6”,“我7”,“中8”,“了9”,“彩票10”]
1.如何让语言模型同时利用上下文
对于传统LM模型来说,我们可以得到许多(输入->输出)样本:
- [“我”] -> “今天”
- [“我”,“今天”] -> “很”
- [“我”,“今天”,“很”] -> “开心”
- …
这些样本的特点是“单向”+“有序”。但是词间的相对位置只能通过输入顺序这一种方式来体现吗?显然不是。例如Transformer就提出了position encoding的概念,来替换通过顺序输入来表征位置关系。因此我们就得到了更灵活的样本选取办法:
- [“我1”] -> “开心4”
- [“我1”,“开心4”] -> “今天2”
- [“我1”,“今天2”,“开心4”] -> “很3”
- …
这就是排列语言模型的核心思想,只要能够给出位置编码信息,就可以代替顺序输入的方式来构建LM模型。从概率模型的角度来看,就是说句子概率 P ( 我,今天,很,开心,逗号,因为,我,中,了,彩票 ) P(我,今天,很,开心,逗号,因为,我,中,了,彩票) P(我,今天,很,开心,逗号,因为,我,中,了,彩票)有不同的分解方式:
对于自回归语言模型: P ( 我 ) P ( 今天 ∣ 我 ) P ( 很 ∣ 我,今天 ) P ( 开心 ∣ 我,今天,很 ) ⋯ P(我)P(今天|我)P(很|我,今天)P(开心|我,今天,很)\cdots P(我)P(今天∣我)P(很∣我,今天)P(开心∣我,今天,很)⋯
对排列语言模型: P ( 我 1 ) P ( 开 心 4 ∣ 我 1 ) P ( 今 天 2 ∣ 我 1 , 开 心 4 ) P ( 很 3 ∣ 我 1 , 今 天 2 , 开 心 4 ) ⋯ P(我_1)P(开心_4|我_1)P(今天_2|我_1,开心_4)P(很_3|我_1,今天_2,开心_4)\cdots P(我1)P(开心4∣我1)P(今天2∣我1,开心4)P(很3∣我1,今天2,开心4)⋯
每一种排列可以记为 z z z,上面的例子就可以写作: z = [ z 1 , z 2 , z 3 , z 4 , ⋯ ] = [ 我 1 , 今 天 2 , 开 心 4 , 很 3 , ⋯ ] z = [z_1,z_2,z_3,z_4,\cdots] = [我_1,今天_2,开心_4,很_3,\cdots] z=[z1,z2,z3,z4,⋯]=[我1,今天2,开心4,很3,⋯]。因此排列语言模型可以看作是自回归语言模型的推广,因为 z z z也可以是原顺序。
可以发现通过重新排列的方式,虽然还是“从左到右”的做预测,但是被预测词现在不但可以看到它的上文,也可以看到它的下文。同时它也避免了BERT里面所有预测词所依赖的上下文信息完全一致的情况,可以认为是一种对双向语境的采样。
2.如何避免标签泄露
首先回忆Transfomer中的self-attention机制,
h i = ∑ j s o f t m a x ( q i T k j ) . v j h_i = \sum_j softmax(q_i^Tk_j).v_j hi=j∑softmax(qiTkj).vj
其中 q i q_i qi是Query向量,Transfomer中对应的是当前位置的状态, k j k_j kj是Key向量,对应的是需要与当前位置做attention的所有位置的状态, v j v_j vj是Value向量,对应的也是需要与当前位置做attention的所有位置的状态。
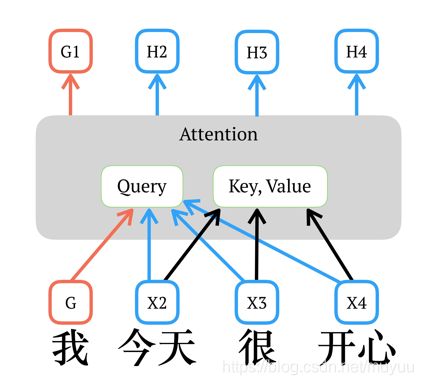
BERT中的Mask机制其实就是将其中预测位置的 q , k , v q,k,v q,k,v均替换成特殊字符[Mask]。但XLNet中,[Mask]不会替换 k 和 v k和v k和v,它只替换Query向量 q q q,因此所有词的表征中都拿不到[Mask]的信息,也就杜绝了它带来的pretrain-finetune差异问题。
但上面这种做法其实只适用于一句话只产生一个样本的情况,如果我们想向自回归模型一样,一次性获得整个句子所有样本的语境表征,这时所有词的表征就必须同时计算,可是这样话就会产生一个矛盾的现象:当某一个词作为被预测词的时候,我们需要得到只包含它位置信息,不包含它内容信息的表征(用来做Query表征);但是这个词与此同时又是别的词的上下文信息,我们又需要知道既包含它内容信息,又包含它位置信息的表征(用来计算其他被预测词的表征)。很自然的想法就是同时维护两套表征,这就是XLNet中提出的"双通道自注意力"。同时计算Content表征 h h h和Query表征 g g g:
g 1 l = a t t e n t i o n ( Q ← g 1 l − 1 , K & V ← h j ≠ 1 l − 1 ) h 1 l = a t t e n t i o n ( Q ← h 1 l − 1 , K & V ← h l − 1 ) \begin{aligned} g_1^l = attention(Q\leftarrow g_1^{l-1},K\&V \leftarrow h_{j\neq1}^{l-1})\\ h_1^l = attention(Q\leftarrow h_1^{l-1},K\&V \leftarrow h^{l-1}) \end{aligned} g1l=attention(Q←g1l−1,K&V←hj=1l−1)h1l=attention(Q←h1l−1,K&V←hl−1)
其中 g 1 l g_1^l g1l表示第一个词在第 l l l层的Query表征, h j ≠ 1 l − 1 h_{j\neq1}^{l-1} hj=1l−1表示第 l − 1 l-1 l−1层除了第一个词之外所有词的Content表征。不难发现Content表征的更新方式与Transformer是一致的。
然而上述注意力机制在多层堆叠时还是会导致标签泄露问题-_-!(没完没了了还。。。)考虑两层的注意力计算:
g 1 l = a t t e n t i o n ( Q ← g 1 l − 1 , K & V ← h j ≠ 1 l − 1 ) h j l − 1 = a t t e n t i o n ( Q ← h j l − 2 , K & V ← h l − 2 ) = a t t e n t i o n ( Q ← h j l − 2 , K & V ← [ h j ≠ 1 l − 2 , h 1 l − 2 ] ) \begin{aligned} g_1^l &= attention(Q\leftarrow g_1^{l-1},K\&V \leftarrow h_{j\neq1}^{l-1})\\ h_j^{l-1} &= attention(Q\leftarrow h_j^{l-2}, K\&V \leftarrow h^{l-2})\\ &= attention(Q\leftarrow h_j^{l-2}, K\&V \leftarrow [h_{j\neq 1}^{l-2},h_1^{l-2}]) \end{aligned} g1lhjl−1=attention(Q←g1l−1,K&V←hj=1l−1)=attention(Q←hjl−2,K&V←hl−2)=attention(Q←hjl−2,K&V←[hj=1l−2,h1l−2])
可以看到 h 1 l − 2 h_1^{l-2} h1l−2会通过 h j l − 1 h_j^{l-1} hjl−1泄露给 g 1 l g_1^l g1l。所以我们还需要对每层注意力使用注意力掩码。对于选定的排列 z z z,将不合理的注意力权重置为零。
g z t l = a t t e n t i o n ( Q ← g z t l − 1 , K & V ← h z 1 : t − 1 l − 1 ) h z t l = a t t e n t i o n ( Q ← h z t l − 1 , K & V ← h z 1 : t l − 1 ) \begin{aligned} g_{z_t}^l = attention(Q\leftarrow g_{z_t}^{l-1},K\&V \leftarrow h_{z_{1:{t-1}}}^{l-1})\\ h_{z_t}^l = attention(Q\leftarrow h_{z_t}^{l-1},K\&V \leftarrow h_{z_{1:t}}^{l-1}) \end{aligned} gztl=attention(Q←gztl−1,K&V←hz1:t−1l−1)hztl=attention(Q←hztl−1,K&V←hz1:tl−1)
其中 z t z_t zt为排列中的第t个词。这样就不会有标签泄露的问题了。
待研究的部分
- 采用Transfomer-XL思想,突破Transformer的最大长度限制
- 采用相对位置编码,而不是绝对位置编码
- 只将结尾 1 K \frac{1}{K} K1的词用来做预测,因为位置太前的词上文太短,不利于收敛,预测效果也不好
实验
以 BERT 为基础,将 BERT 的主干网络从 Transformer 换成 Transformer-XL 后,在需要建模较长上下文的阅读理解任务 RACE 和 SQuAD2.0 均有比较明显地提升(对比1&2行)。而在此基础上加上乱序语言模型后,在所有任务上都有不同程度的提升(对比2&3行)。