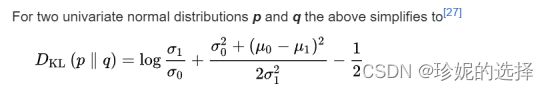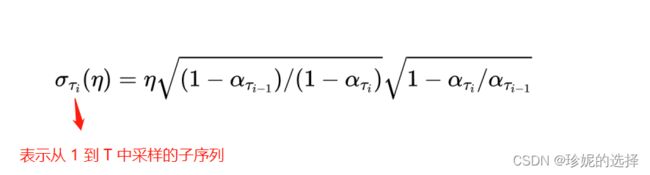Stable Diffusion 原理介绍与源码分析（二、DDPM、DDIM、PLMS算法分析）

Stable Diffusion 原理介绍与源码分析（二、DDPM、DDIM、PLMS）

系列文章

• Stable Diffusion 原理介绍与源码分析（一、总览）

前言（与正文无关，可忽略）

发现标题越起越奇怪了…

本文继续介绍 Stable Diffusion 框架的实现。在之前的文章 Stable Diffusion 原理介绍与源码分析（一、总览） 中，我介绍了 Stable Diffusion 文生图框架的整体结构，如下图，并简要描述了其各个重要组成模块：

其中红框中的 UNetModel 已经在上篇文章中介绍过，只需要记住它被用来预估图像的噪声，并且可以保持输入输出的大小不变（我就是这么进行粗浅的记忆的）。而本文则会将目光移向采样阶段，即上图蓝框中的内容，简要介绍扩散模型使用 DDPM、DDIM、PLMS 等算法通过迭代去除噪声，从而生成图像的潜在空间（latent space）表示。

另外需要注意的是，我其实在文章（一）中也进行过说明，我将以伪代码的形式对源码进行分析，这可以刨除大量无关的细节，直达本质，也特别方便后续回顾。

目前 ChatGPT 大火，它能够在一定程度上辅助我们写代码，我们只需要准确描述自己的意图，剩下的工作让它完成就好。（以后和公司谈薪时，对代码进行 Ctrl-C & Ctrl-V 只值 1% 的工资，知道 Ctrl-C & Ctrl-V 哪些 code 值剩下的 99%，哈哈）

总览

本文对 Stable Diffusion 主要使用的如 DDPM、DDIM、PLMS 等算法进行分析，详解其代码实现。

源码地址：Stable Diffusion

DDPM

对原理进行朴素回顾

DDPM （Denoising Diffusion Probabilistic Models）算法之前在 扩散模型 (Diffusion Model) 简要介绍与源码分析 介绍过，推导有些复杂，这里就用朴素的大白话描述一下我觉得最重要的几个公式，然后分析代码实现，核心是理清楚推导的逻辑链。

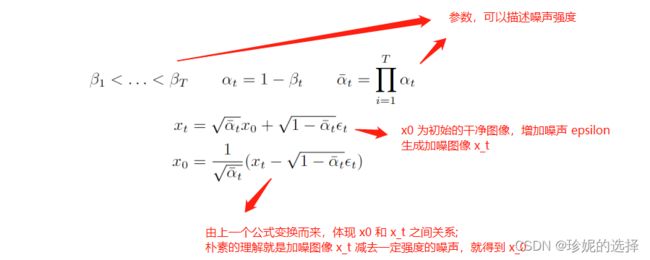
首先扩散模型的整个思路是先在图像上不断的加噪，从而对图像进行破坏，然后再对破坏后的图像进行不断的去噪，最后恢复出原始图像。这个过程可以用如下公式描述：

现在的一个问题是如何求逆向阶段的分布，也就是如果给定了一张加噪的图像，我们如何才能求得它前一时刻没有被破坏的那么严重的图像。经过数学高手们的一顿推导，发现两个重要结论：1. 逆向过程也服从高斯分布；2. 在知晓初始干净图像的情况下，我们能通过贝叶斯公式将逆向过程转换成前向过程，从而算出逆向过程的分布; 在公式上体现如下：

算出逆向过程的分布后，我们就可以训练一个模型，去尽力拟合这个分布，那么模型预估出来的结果也应该服从高斯分布：

现在逆向过程的分布有了（可以理解为 label），模型的预估分布也有了，就差一个 Loss 函数，而经过数学高手的又一顿推导，发现 Loss 居然是计算两个分布的 KL 散度，而且还是两个高斯分布的 KL 散度！朴素的说，KL 散度可以用来描述两个分布之间的差距。不得不感慨，数学就是这么神奇，左推右推，最后能得到一个美妙的结果：

多元高斯分布的 KL 散度是有闭式解的，详见维基百科：https://en.wikipedia.org/wiki/Kullback%E2%80%93Leibler_divergence#Multivariate_normal_distributions，具体公式如下：

最后得到训练过程和采样过程分别如下：

下面进行代码分析。

DDPM 代码分析

再次提醒，我对源码进行了抽象，以伪代码的形式呈现。详细列出每行代码完全没有必要，太多的细节会淹没真正重要的信息。另外注意两点：1. 在实现上，我保持类名、函数名和源码一致，这样就可以方便快速了解类或者函数的功能；2. 函数尽量按调用顺序进行组织；

Stable Diffusion 对 DDPM 的实现源码地址：https://github.com/CompVis/stable-diffusion/blob/main/ldm/models/diffusion/ddpm.py

• 训练阶段：

不客气的说，非常简洁。PyTorch 中 forward() 函数是入口，输出噪声之间的 Loss；

• 采样阶段：

按顺序阅读，核心在 p_sample 函数中，使用重参数技巧生成样本：

针对 DDPM 的改进

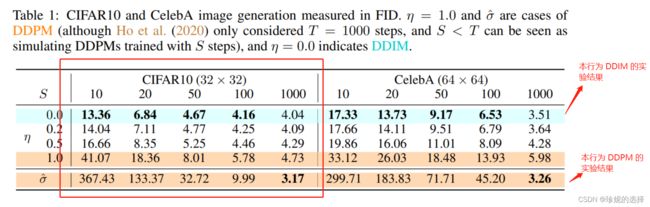
下面简单介绍 DDIM 和 PLMS算法，它们均是对 DDPM 算法的改进。DDPM 在采样阶段需要迭代很多次（比如 1000）才能得到一个比较好的效果，而 DDIM、PLMS 算法则尝试使用较少的迭代次数来加速采样过程。下图是 DDIM 论文中给出的实验结果分析：

其中第一行（绿线…）是 DDIM 的结果，最后一行是 DDPM 的实验结果，使用 FID 来评估生成图像的质量，该值越小，表示结果越好；S 为迭代次数，只看红框中的 CIFAR10 数据集上的效果，可以发现随着迭代次数的增加，FID 越小，生成图像质量越好；另外可以注意到 DDIM 迭代到第 50 次左右时，就几乎能达到 DDPM 迭代到 1000 次的效果 （4.67 vs. 3.17）;

DDIM

DDIM 将图像的采样过程定义为非马尔科夫链:

并重新推导了图像的生成公式：

其中 ${\sigma }_t$ 定义如下：

根据推导，如果系数 $\eta =1$, 那么此时采样过程和 DDPM 相同；而当系数 $\eta =0$ 时，即为 DDIM 算法的采样过程，注意到此时均方差为 0，图像的生成过程是确定的。另外需要注意在 DDIM paper 的公式中，${\alpha }_t$ 以及 ${\beta }_t$ 等的含义和 DDPM 论文中不同，它们被重新定义了…

Stable Diffusion 中，DDIM 的源码实现位于：https://github.com/CompVis/stable-diffusion/blob/main/ldm/models/diffusion/ddim.py

伪代码如下（DDIM 默认只迭代 50 步）：

PLMS

没有详细进行公式推导，平时加班就已经很辛苦了： 逃避虽然可耻，但是有用 …

论文中给出采样过程的公式如下：

伪代码如下：

资源汇总

• Stable Diffusion: https://github.com/CompVis/stable-diffusion
• DDPM 相关资料
  • 论文：Denoising Diffusion Probabilistic Models | https://arxiv.org/abs/2006.11239
  • 代码：tf version: https://github.com/hojonathanho/diffusion | pytorch version: https://github.com/lucidrains/denoising-diffusion-pytorch
• DDIM 相关资料
  • 论文：Denoising Diffusion Implicit Models | https://arxiv.org/abs/2010.02502
  • 代码：https://github.com/ermongroup/ddim
• PNDM/PLMS 相关资料
  • 论文：Pseudo Numerical Methods for Diffusion Models on Manifolds | https://openreview.net/forum?id=PlKWVd2yBkY
  • 代码：https://github.com/luping-liu/PNDM

小结

本文对 Stable Diffusion 使用的如 DDPM、DDIM、PLMS 等算法进行了简要分析，用伪代码的形式介绍了其实现过程。

逃避了对 DDIM 和 PLMS 中的公式推导，虽然可耻，但真的有用。。。。最后附上一张 AI 产出的 Image，让疲劳的眼睛休息下：

(对了，可以在微信中搜索 “珍妮的算法之路” 或者 “world4458” 关注我的微信公众号, 及时获取最新原创技术文章更新。。。）