Java十大经典排序算法
目录
-
- 1. 插入类排序
-
- 1.1 直接插入排序
- 1.2 希尔排序
- 2. 选择类排序
-
- 2.1 直接选择排序
- 2.2 堆排序
- 3. 交换类排序
-
- 3.1 冒泡排序
- 3.2 快速排序（递归）
-
- 3.2.1 快排的优化
- 3.3 快速排序（非递归——栈）
- 4. 归并类排序
-
- 4.1 二路归并排序（递归）
- 5. 基于比较的排序总结
- 6. 非比较类排序
-
- 6.1 计数排序
- 6.2 基数排序
- 6.3 桶排序
1. 插入类排序
1.1 直接插入排序
- 思想：
可以理解为打扑克牌的时候，给扑克牌会进行插入排序。
①一开始抓到一张“3”，默认是有序的；
②第二次抓到“5”，与3比较，比3大，应该插入在3的后面；
③第三次抓到“4”，与5比较，比5小，则把5后移一个位置，继续与3比较，比3大，因此插入到“3”和“5”之间。
注意：需要一开始就用tmp记录待插入的值，不然会导致最后值被覆盖。
即，把n个元素分为有序列和无序列，刚开始时，有序列默认是1个元素，无序列时剩余的n-1个元素，每次从无序列种取出1个元素与有序列进行排序，最终得到一个排序好的有序列。
- 实现：
public static void insertSort(int[] nums) {
for (int i = 1; i < nums.length; i++) {
int tmp = nums[i];
int j = i-1;
for (; j >= 0; j--) {
if (tmp < nums[j]) {
nums[j+1] = nums[j];
}else {
break;
}
}
nums[j+1] = tmp;
System.out.println("第"+ i + "次排序后结果为：" +Arrays.toString(nums));
}
}
- 分析：
稳定性：稳定
时间复杂度：O(n的平方)【最坏】，O(n)【最好】，O(n的平方)【平均】
空间复杂度：O(1)
元素越有序，直接插入排序速度越快【对数据敏感】
运行结果：
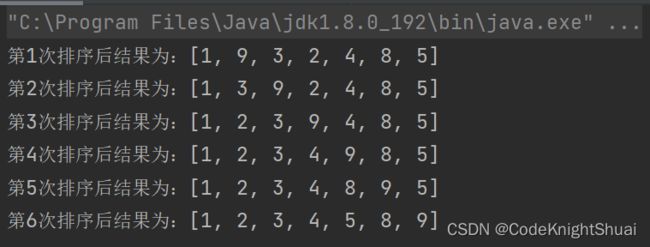
序列为int[] nums = {9,1,3,2,4,8,5};
默认有序列{9}，无序列{1,3,2,4,8,5}
①待排序{1}排序后，有序列{1,9}，无序列{3,2,4,8,5}
记录1（防后移被覆盖），1比9小，所以需要将9后移，最后将1放在空位（9原本的位置）
②待排序{3}，排序后，有序列{1,3,9}，无序列{2,4,8,5}
记录3（防后移被覆盖），3比9小，所以需要将9后移，3比1大，所以将3放在1和9之间（9原本的位置）
③待排序{2}，排序后，有序列{1,2,3,9}，无序列{4,8,5}
记录2（防后移被覆盖），2比9小，所以需要将9后移，2比3小，所以需要将3后移，2比1大，所以将2放在1和3之间（3原本的位置）
④待排序{4}，排序后，有序列{1,2,3,4,9}，无序列{8,5}
记录4（防后移被覆盖），4比9小，所以需要将9后移，4比3大，所以将4放在3和9之间（9原本的位置）
⑤待排序{8}，排序后，有序列{1,2,3,4,8,9}，无序列{5}
记录8（防后移被覆盖），9比9小，所以需要将9后移，8比4大，所以将8放在4和9之间（9原本的位置）
⑥待排序{5}，排序后，有序列{1, 2, 3, 4, 5, 8, 9}，无序列{}
记录5（防后移被覆盖），5比9小，所以需要将9后移，5比8小，所以需要将8后移，5比4大，所以将5放在4和8之间（8原本的位置）
1.2 希尔排序
- 思想：
希尔排序是直接插入排序的优化，又叫缩小增量排序。
把整体元素以gap为间距进行分组，每组之间进行直接插入排序，排序完之后再以gap/2继续排序，直至gap为1为止。
本质是插入排序，只不过这个插入排序和gap有关系。
跳跃式的分组排序，可以尽量把小的数据快速往前移，把大的数据快速往后移（相对于相邻分组的好处）。
- 实现：
//控制增量gap的方法
public static void shellSort(int[] nums) {
int gap = 5;
while (gap >= 1) {
shell(nums,gap);
gap = gap / 2;
}
}
//真正排序的方法
public static void shell(int[] nums, int gap) {
//直接插入排序+希尔
for (int i = gap; i < nums.length; i += gap) {
int tmp = nums[i];
int j = i - gap;
for (; j >= 0; j -= gap) {
if (nums[j] > tmp) {
nums[j+gap] = nums[j];
}else {
break;
}
}
nums[j + gap] = tmp;
}
}
- 分析：
稳定性：不稳定
时间复杂度：O(n的1.3平方)【估计】，与gap增量有关
空间复杂度：O(1)
元素越有序，直接插入排序速度越快（理解成插入排序的优化）【对数据敏感】
序列为：{9,1,3,2,4,8,5,9,2,5,6,10}
①gap = 5；排序后为{6, 1, 3, 2, 4, 8, 5, 9, 2, 5, 9, 10}
②gap = 2；排序后为{2, 1, 3, 2, 4, 5, 5, 8, 6, 9, 9, 10}
③gap = 1；排序后为{1, 2, 2, 3, 4, 5, 5, 6, 8, 9, 9, 10}
每组的排序都是直接插入排序，数据在慢慢的变有序，插入排序的优点是越有序越快，所以不用担心每组的数据在在慢慢变多。
2. 选择类排序
2.1 直接选择排序
- 思想：
从待排序的元素中，每次直接选择出最小的元素放入已经排好序的序列中，以此类推。
每次默认待排序的元素是最小的，与其后面的无序的序列进行比较，如果有比它小的，则进行交换，以此类推，当无序序列走完的时候，可以选出最小的放入到排序好的序列后面。
- 实现：
public static void select(int[] nums) {
for (int i = 0; i < nums.length; i++) {
for (int j = i + 1; j < nums.length; j++) {
if (nums[i] > nums[j]) {
int tmp = nums[i];
nums[i] = nums[j];
nums[j] = tmp;
}
}
}
}
//或者把交换封装成方法
public static void select(int[] nums) {
for (int i = 0; i < nums.length; i++) {
int min = i;
int j = i + 1;
for (; j < nums.length; j++) {
if (nums[min] > nums[j]) {
min = j;
}
}
if (min != i) {
swap(nums,min,i);
}
}
}
private static void swap(int[] nums, int min, int i) {
int tmp = nums[min];
nums[min] = nums[i];
nums[i] = tmp;
}
- 分析：
稳定性：不稳定【2 3 2 1 ，这样第一次会变成 1 3 2 2，2的相对位置发生了改变，所以是不稳定的】
时间复杂度：O(n的平方)【没有好坏之分】
空间复杂度：O(1)
对数据不敏感，不管怎么样，都得把后面的比较完【不太适用】
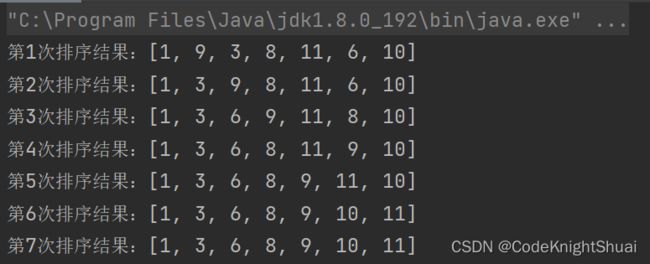
待排序序列为：9,1,3,8,11,6,10
①默认记录9为最小元素，1比9小，1和9交换位置（或者记录1为最小元素），后面的元素都没有比1小，故排序后结果为：[1, 9, 3, 8, 11, 6, 10]
②默认记录9为最小元素，3比9小，3和9交换位置，后面的元素都没有比3小，故排序后结果为：[1, 3, 9, 8, 11, 6, 10]
③默认记录9为最小元素，8比9小，8和9交换位置，6比8小，6和8交换位置，故排序后蝶国为：[1, 3, 6, 9, 11, 8, 10]
④默认记录9为最小元素，8比9小，8和9交换位置，[1, 3, 6, 8, 11, 9, 10]
⑤默认记录11为最小元素，9比11小，9和11交换位置，故排序后的结果为：[1, 3, 6, 8, 9, 11, 10]
⑥默认记录11为最小元素，10比11小，10和11交换位置，故排序后的结果为：[1, 3, 6, 8, 9, 10, 11]
⑦默认记录11为最小元素，11之后没有待排序的元素序列，故最终排序结果为：[1, 3, 6, 8, 9, 10, 11]
2.2 堆排序
- 思想：
从小到大排序：建大根堆（堆顶元素是最大的，每次把堆顶元素与堆的最后一个元素进行交换，再重新调整堆，从而得到从小到大的序列）
从大到小排序：建小根堆（堆顶元素是最小的，每次把堆顶元素与堆的最后一个元素进行交换，再重新调整堆，从而得到从大到小的序列）
整体分2步：建堆+堆删除（都是向下调整算法）
- 实现：
class Solution {
public int[] sortArray(int[] nums) {
for (int i = (nums.length - 1 - 1) / 2; i >= 0; i--) {
shiftDown(i,nums.length,nums);
}
int end = nums.length - 1;
while (end > 0) {
swap(nums,0,end);
shiftDown(0,end,nums);
end--;
}
return nums;
}
private void swap(int[] nums, int min, int i) {
int tmp = nums[min];
nums[min] = nums[i];
nums[i] = tmp;
}
public void shiftDown(int parent, int len, int[] nums) {
int child = parent * 2 + 1;
while (child < len) {
if (child + 1 < len && nums[child] < nums[child+1]) {
child = child +1;
}
if (nums[child] < nums[parent]) {
break;
}else {
swap(nums,child,parent);
parent = child;
child = parent * 2 + 1;
}
}
}
}
- 分析：
稳定性：不稳定
时间复杂度：O(nlogn）
空间复杂度：O(1)
对数据不敏感，堆排序的前提是要建立一个大根堆/小根堆
①建立大根堆（向下调整）
②每次堆顶元素和堆尾元素交换，除去交换后的堆尾元素重新调整成堆，用end记录堆尾元素的位置，注意end是一直在变的。【换完了，就调整】
3. 交换类排序
3.1 冒泡排序
- 思路：
冒泡排序，前后两个元素两两比较，不满足排序情况则进行交换，就像冒泡一样，最后最大的元素像泡泡一样到了序列的最后面。
- 实现：
①基础优化版
//冒泡排序
public static void bubbleSort(int[] nums) {
for (int i = 0; i < nums.length - 1; i++) {
for (int j = 0; j < nums.length - 1 - i; j++) {
if (nums[j] > nums[j+1]) {
swap(nums,j,j+1);
}
}
}
}
private static void swap(int[] nums, int i, int j) {
int tmp = nums[i];
nums[i] = nums[j];
nums[j] = tmp;
}
②进阶优化版
我们发现如果某一趟没有发生元素交换则说明该序列已经有序了，因此可以设置标志位判断在一趟这元素有没有发生交换
public static void bubbleSort(int[] nums) {
for (int i = 0; i < nums.length - 1; i++) {
boolean flag = false;
for (int j = 0; j < nums.length - 1 - i; j++) {
if (nums[j] > nums[j+1]) {
flag = true;
swap(nums,j,j+1);
}
}
if (flag == false) {
break;
}
}
}
private static void swap(int[] nums, int i, int j) {
int tmp = nums[i];
nums[i] = nums[j];
nums[j] = tmp;
}
- 分析：
稳定性：稳定
时间复杂度：O(n的平方）
空间复杂度：O(1)
对数据敏感，如果一趟没有发生数据交换，则说明元素已经有序
外层循环表示需要冒泡排序的趟数
内层循环表示需要比较的元素个数
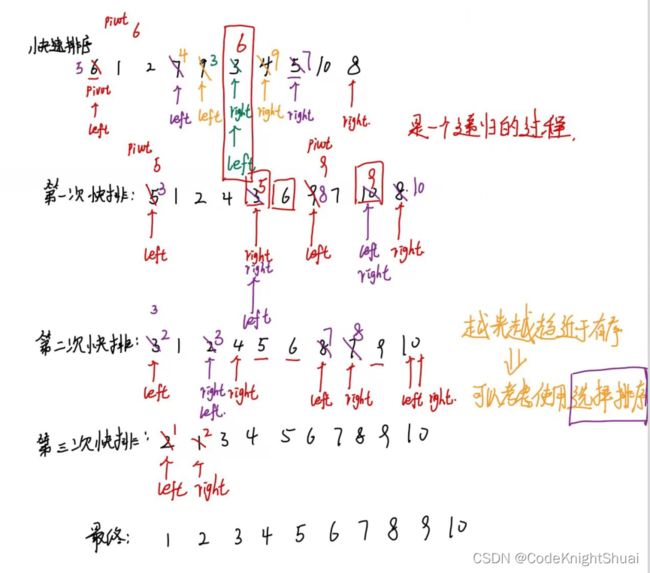
3.2 快速排序（递归）
- 思路：
选定一个数为基准，比基准小的元素全放在基准左边，比基准大的元素全放在基准右边，左边和右边又递归重复上述过程，直到所有元素都排列在相应位置上。
是一种基于二叉树结构的交换排序
- 实现：
//快速排序
public static void quickSort(int[] nums) {
quick(nums,0,nums.length-1);
}
//完成递归操作
public static void quick(int[] nums, int left, int right) {
if (left >= right) {
return;
}
int div = partition(nums,left,right);
quick(nums,left,div-1);
quick(nums,div+1,right);
}
//基准划分操作
public static int partition(int[] nums, int left, int right) {
int pivot = nums[left];
while (left < right) {
while (left < right && nums[right] >= pivot) {
right--;
}
nums[left] = nums[right];
while (left < right && nums[left] <= pivot) {
left++;
}
nums[right] = nums[left];
}
nums[left] = pivot;
return left;
}
-
分析：
稳定性：不稳定（前后交换）
时间复杂度：O(nlogn）【最好，满二叉树，完全二叉树，每次都能均匀分割待排序序列】，O(n平方)【最坏，有序/逆序，相当于只有左树/右树】
空间复杂度：O(logn)【左树/右树高顿】，最坏为O(n)
对数据敏感，元素越有序，快排越低效
①递归的出口为什么要取大于号？
假设待排序序列为1 2 3 4
那么基准为1，left为0，right为3
right开始往前走，走到0位置和left相遇，方法结束
下一次，left为0，right为-1，因此也不可以进行递归，而需直接返回，所以要取大于等于号。
②循环的条件为什么要取等号？
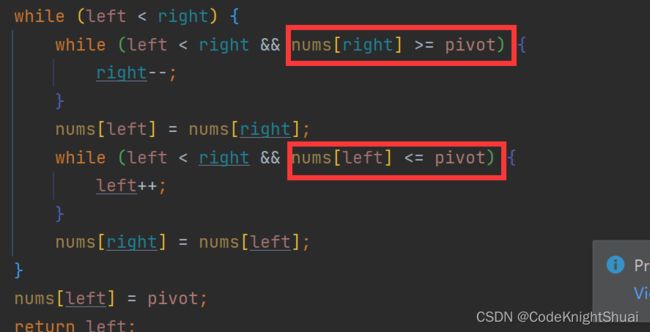
假设不取等号，前后2个元素相等的情况下，会陷入死循环。
例如，待排序序列为6 3 4 5 7 6，则会在第一个元素和最后一个元素之间反复横跳。
③左边作为基准，为什么要先从右边开始走，而不先从左边走？
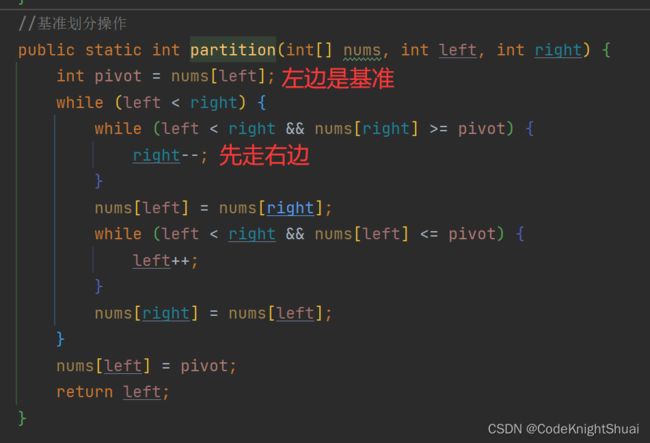
用Hoare法比挖坑法好解释。
最终会造成把比基准大的数换到前面去。
快排有3种方法（是一个递归过程）
①Hoare版：left去找比基准小的，right去找比基准大的，找到之后两者进行交换。
②挖坑法：right去找比基准小的，放到left空出来的坑里，left去找比基准大的，放到right空出来的坑里。
③前后指针
3.2.1 快排的优化
快排递归的次数太多了，会导致栈溢出。
- 三数取中法选基准
对于基准值的选取，如果选取不当，可能导致最坏情况出现，那么可以采用三数取中法选择基准值
第一个数 中位数 最后一个数 【选择中间大的数字为基准】
找到中数后，和第一位位置的数进行交换，然后作为基准。
这样就可以尽量保证是一颗均匀的二叉树 - 递归到小的子区间时，考虑使用插入排序
快速排序越到后面，子区间越小，数据也越趋于有序，此时可以考虑使用插入排序提高效率，注意是对子区间进行插入排序，不是对整体进行插入排序。
3.3 快速排序（非递归——栈）
用栈去模拟递归左边和递归右边
栈用来存小区间的两端的下标
要保证小区间至少有2个元素，才把区间下标入栈
然后每次出栈2个，重新定位小区间，
//快速排序非递归
public static void quickSortNot(int[] nums) {
int left = 0;
int right = nums.length - 1;
Deque<Integer> stack = new LinkedList<>();
int div = partition(nums,left,right); //挖坑法
//判断是否有2个元素
if (left +1 < div) {
stack.push(left);
stack.push(div-1);
}
if (div + 1 < right) {
stack.push(div+1);
stack.push(right);
}
while (!stack.isEmpty()) {
right = stack.pop();
left = stack.pop();
div = partition(nums,left,right);
if (left +1 < div) {
stack.push(left);
stack.push(div-1);
}
if (div + 1 < right) {
stack.push(div+1);
stack.push(right);
}
}
}
4. 归并类排序
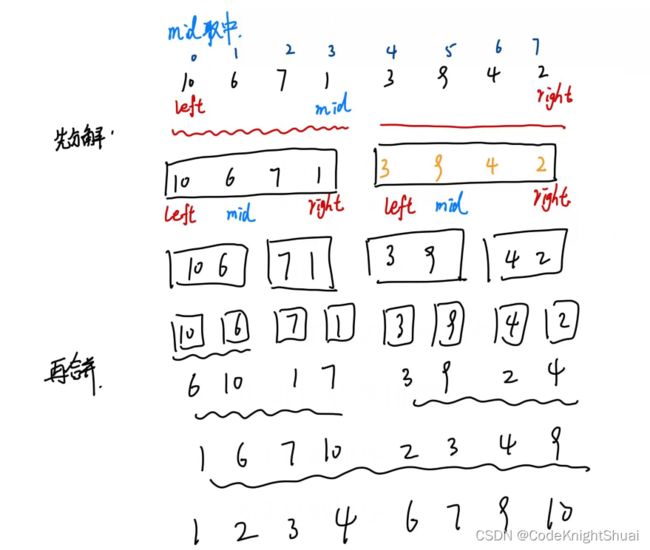
4.1 二路归并排序（递归）
- 思路：
先两两分解，再两两合并
先将序列元素分解成为独个的，有序表中只有一个元素分解结束，再两两合并成有序的，即将已有序的子序列合并，得到完全有序的序列，先让每个子序列有序，再使子序列段间有序。
- 实现：
//归并排序
public static void mergeSort(int[] nums) {
//先分解
divM(nums, 0 ,nums.length-1);
}
//递归分解
public static void divM(int[] nums, int left, int right) {
if (left >= right) {
return;
}
int mid = left + (right - left) / 2;
divM(nums,left,mid);
divM(nums,mid+1,right);
//合并
merge(nums,left,right,mid);
}
//合并
public static void merge(int[] nums, int left, int right, int mid) {
int s1 = left;
int s2 = mid + 1;
int[] tmp = new int[right - left +1]; //额外开辟的空间
int k = 0; //tmp数组的下标
while (s1 <= mid && s2 <= right) {
if (nums[s1] <= nums [s2]) {
tmp[k++] = nums[s1];
}else {
tmp[k++] = nums[s2];
}
}
while (s1 <= mid) {
tmp[k++] = nums[s1];
}
while (s2 <= right) {
tmp[k++] = nums[s2];
}
//现在tmp已经有序了，但不是在原来数组上排序的
//把tmp数组放到原数组上
for (int i = 0; i < tmp.length; i++) {
nums[i + left] = tmp[i];
}
}
- 分析：
稳定性：稳定**
时间复杂度**：O(nlogn）
【快排和归并都是nlogn，但还是快排的速度快，可以理解为nlogn前面有系数，快排的系数比归并小，所以快排更快】
空间复杂度：O(n)会为临时数组开辟内存空间int[] tmp = new int[right - left +1]; //额外开辟的空间
对数据不敏感，任何序列都需要经过 分解+合并 两个过程
5. 基于比较的排序总结
- 稳定性
只有3个排序是稳定的：插入排序、冒泡排序、归并排序 - 对数据不敏感
只有3个排序对数据不敏感：选择排序、堆排序、归并排序 - 时间复杂度（最坏情况下）
①插入类排序
直接插入排序：O(n的平方)
希尔排序：O(n的1.3次方)【平均的，局部估计，与gap有关，分组进行插入排序】
②选择类排序
选择排序：O(n的平方)
堆排序：O(nlogn)【前提一定要先建堆】
③交换类排序
冒泡排序：O(n的平方)
快速排序：O(nlogn)【最好情况下】
④归并排序
二路归并排序：O(nlogn)
只有3个排序时间复杂度是nlogn：堆排序、快速排序、归并排序 - 空间复杂度
只有2个排序的空间复杂度不是O(1)：快速排序O(logn)、归并排序O(n)
6. 非比较类排序
不能比较数字之间的大小而进行的排序。
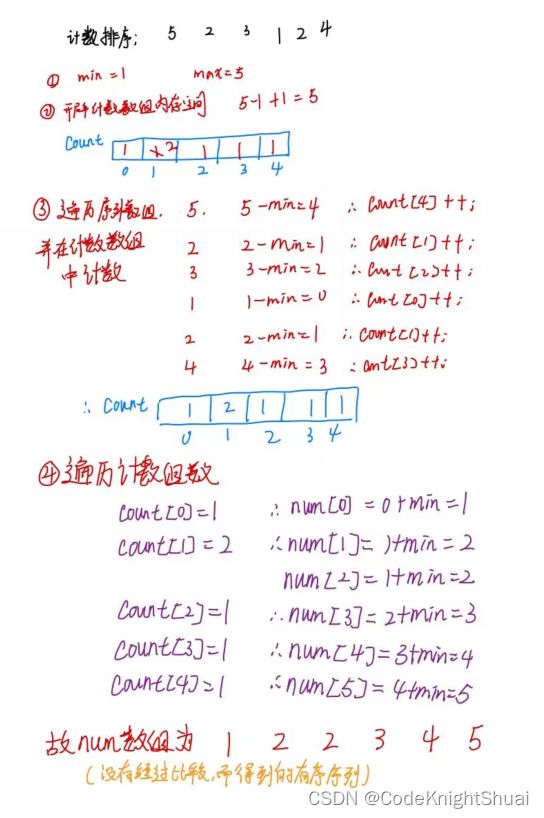
6.1 计数排序
- 思路：
①找到给定序列中的最小元素值和最大元素值 ②新建一个计数数组，数组的长度由第一步找到的最小值和最大值确定的范围而定
③遍历序列数组，对应计数数组的下标对其进行计数的操作 ④遍历计数数组，将计数数组中值不是0的下标对应复制到序列数组中，即排好序了
- 适用场景
一组集中在某个范围的数据，因为如果不集中就会浪费计数数组的很多内存空间。 - 实现：
public static void countSort(int[] nums) {
int min = nums[0];
int max = nums[0];
//找最大值和最小值
for (int i = 1; i < nums.length; i++) {
if (min > nums[i]) {
min = nums[i];
}
if (max < nums[i]) {
max = nums[i];
}
}
//新建计数数组
int[] count = new int[max - min + 1];
//遍历序列数组，并且用计数数组计数
for (int i = 0; i < nums.length; i++) {
count[nums[i] - min]++;
}
//遍历计数数组
int k = 0;
for (int i = 0; i < count.length; i++) {
while (count[i] != 0) {
nums[k] = i + min;
k++;
count[i]--;
}
}
}
- 分析：
稳定性：稳定**
时间复杂度**：O(max(n,计数数组范围)）
空间复杂度：O(计数数组范围)
注意：计数排序在数据范围集中时效率很高，但是适用范围及场景有限。
6.2 基数排序
- 思路：
建立0到9也就是10个基数捅， 先按照个位排序，将个位放置对应的记述桶内 再依次取出 先按照使位排序，将十位放置对应的记述桶内 再依次取出
直至最高位，循环上述操作
- 分析：
①进出的次数和最大值的位数有关
②基数桶可以用队列来表示
原始序列：123 99 678 93 58 77 65 54 26
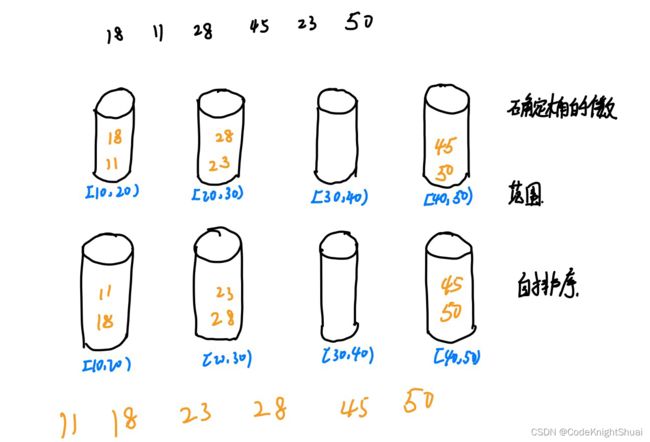
6.3 桶排序
- 思路：
划分多个范围相同的区间
每个子区间自排序
合并
- 分析：
