C语言数据结构+快速排序+快速排序实现流程+快速排序代码实现

一.快速排序实现思路

通过在数组中找一个基准值(默认情况下初始我们都是以数组第一个元素为基准值)对数组进行分划,首先定义两个指针,一个left,一个right,分别是指向数组的第一个和最后一个元素使用基准值从right往前依次比较,直到找到第一个小于基准值的数,把它放到基准值所在位置,然后再用基准值对数组从left往右依次比较直到找到第一个大于基准值的元素,然后把这个元素放到right的位置,最后把基准值放到放到前面left所指向的位置.在这个的基础上利用递归的方式实现这个完整的快速排序

二.快速排序的实现流程

1.初始化一个数组

第一趟排序
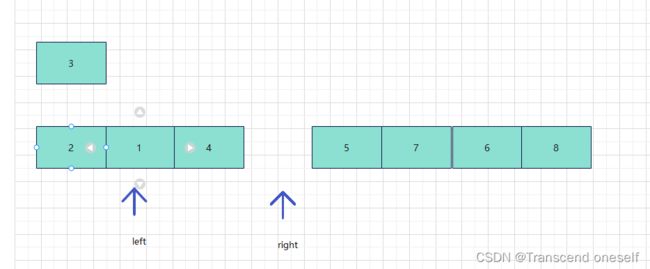
定义一个变量pivot来暂存我们的基准值,此时我们把arr[left] (数组的第一个元素为基准)
首先我们从right依次往左边找,找到所有小于基准值的数放到arr[left]的位置,也就是我们上面数组的元素2,

把此时right对应元素放到left对应元素位置

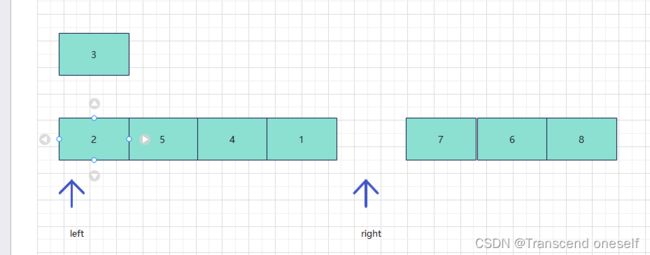
第二我们从left依次往右边找,找到所有大于pivot基准的数,也就是我们上面的元素5

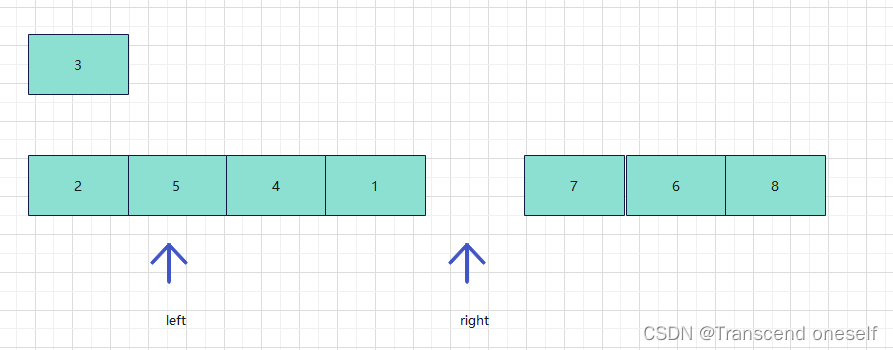
把这个元素放到前面arr[right] (前面2)的位置,然后把基准值放到当时arr[left] (前面5)的位置,

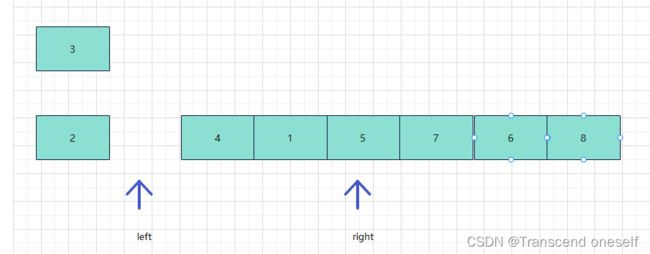
此时的left还未与right相交说明还未找完
继续开始从right往右边寻找比基准值小的数,

此时的left还未与right相交说明还未找完
继续开始从right往右边寻找比基准值小的数,
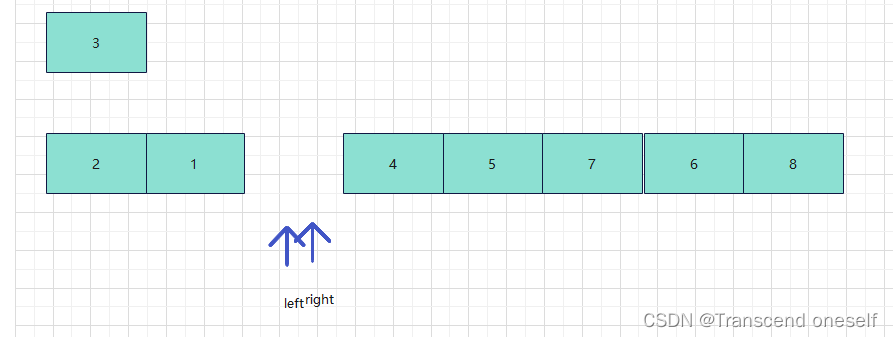
可以看到第一轮从右开始往左边找,找到之前right就会与left相交,说明此时基准值的位置就确定在了left和right相交的位置

最后第一轮排序后数组为:

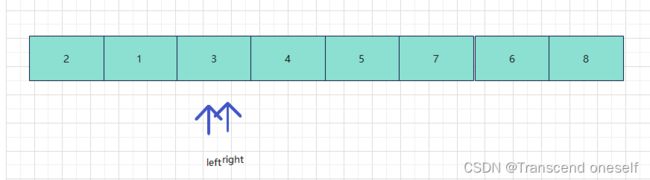
最后把基准此时的下标返回给主调函数,表示这个下标对应元素已经排好序了,以此对数组的未排序部分做了划分

第二趟排序

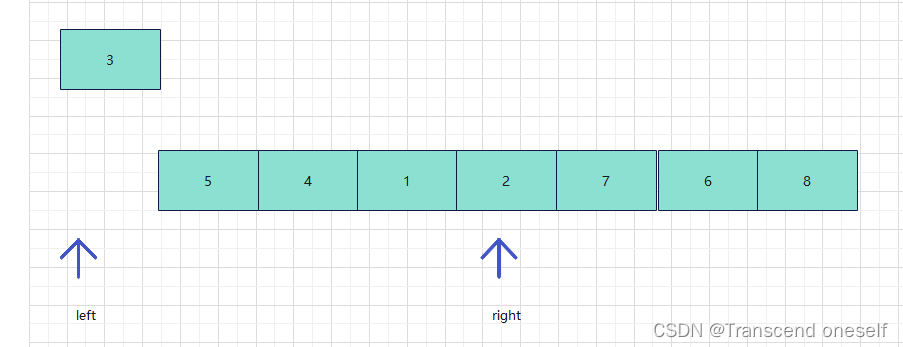
这次排序会通过上一趟排序返回的基准下标,对数组进行划分,从而对未排序的区域排序
此处可以清楚的看到通过上一轮的排序我们已经把小于基准值的元素都放到了基准值的左边,大于基准值的元素放在在基准值的右边

然后通过递归去让未排序部分也去进行我们的快速排序
通过第一轮返回的下标(index)可以知道,未排序的两个区域为(left,index-1)和(index+1,right)

一直递归下去,直到排序区域的左右下标指针指向的是同一个元素才停止递归,此时也说明我们的快速排序已经排好序了

三.伪代码实现

int quick_sort(int arr[],int left,int right)
{
	int pivot = arr[left];//以数组的第一个元素为基准
	while (left < right)
	{
		//从右边寻找小于pivot的值
		while (left<right && arr[right]>=pivot)//left
		{
			right--;
		}//找到之后把arr[right]放到pivot位置
		arr[left] = arr[right];
		while (left < right && arr[left]<=pivot)//从左边往右边查找比pivot大的数
		{
			left++;
		}//找到之后把arr[left]放到前面arr[right]位置
		arr[right] = arr[left];		
	}
	//最终把基准值放到left和right相交的位置
	arr[left] = pivot;
	return left;

}

void part_arr(int arr[],int left,int right)
{
	if (left < right)
	{
		int index = quick_sort(arr, left, right);
		part_arr(arr,left,index-1);//左子表
		part_arr(arr,index+1,right);//右子表
	}
}
int main()
{
	int arr[] = { 3,5,4,1,2,7,6,8 };
	int sz = sizeof(arr)/sizeof(arr[0]);
	int left = 0;
	int right = sz - 1;
	part_arr(arr,left,right);
	for (int i = 0; i <= 7; i++)
	{
		printf("%d ", arr[i]);
	}
	return 0;

运行结果

四.总结

快速排序的时间复杂度最好的情况就是它的递归层数*n,空间复杂度为它的递归层数
最坏的情况下就是这个数组原本为有序表或者一个逆序表的时候,它的复杂度会达到O(n^2),为了解决这种情况我们可以通过改变基准值的选法来使得数组更加均匀,比如我们可以把基准定在数组尾部或者中间等位置,这样就可以使得数组更均匀,是快速排序在一些特殊情况下也可以有较高效的排序效率.