数据结构--链式栈与链式队列设计与实现(c++描述)
链式栈与链式队列的设计与实现(c++描述)
本文主要讨论的是链式栈与链式队列的设计思想与实现对于链表的基本知识此处不予过多讨论
链式栈
链栈结构描述
几点解释说明:
- 此处栈顶指针也即表头指针,因为此处选择的链表为单向链表,无法从当前结点得出其前驱结点,由于栈的操作均在一端进行因此将栈顶指针设在表头更便于进行出栈和入栈
- 此处我选择使用count主要是因为考虑到如果说要获取栈内元素个数时,通过count能节省再去遍历链表获得存储空间造成的时间浪费,属于以空间换时间。
- 由于是链式结构,存储空间是我们new出来在堆上的并不会在结束运行时自动释放存储空间因此我们需要调用析构函数进行存储空间释放
- error_code 是一个枚举类型,有success、fail两个类型常量来进行标识操作是否成功
链结点代码
结点的设计固定直接上代码
#ifndef LINK_NODE_H
#define LINK_NODE_H
// 链表结点类的定义
#include<iostream>
template<class T>
struct LinkNode{
T data;
LinkNode<T> *next;
LinkNode(LinkNode<T>* ptr = NULL){
next = ptr;
}
LinkeNode(T value){
data = value;
next = NULL;
}
};
#endif
函数的具体设计思路与实现
Linked_stack()
此函数是构造函数主要是初始化栈结构相对简单直接上代码
// 构造函数
template<class T>
Linked_stack<T>::Linked_stack(){
count = 0;
top = NULL;
}
~Linked_stack()
析构函数,要进行的操作是释放存储空间。我是用的是clear()函数,clear()函数是用来清空栈的,完全可以在此处使用
// 构造函数
template<class T>
Linked_stack<T>::~Linked_stack(){
clear();
}
bool empty()
判断栈是否为空,通过count来进行判断
template<class T>
bool Linked_stack<T>::empty()
{
return count==0;
}
error_code push(elementType x)
将元素压入栈,因为是链式存储结构因此一般不会出现栈空间不足的情况,这里可以加个判断
template<class T>
error_code Linked_stack<T>::push(T x){
LinkNode<T>* s = new LinkNode<T>(x);
if(s != NULL)
{
s->next = top;
top = s;
count++;
return success;
}
else{
return fail;
}
}
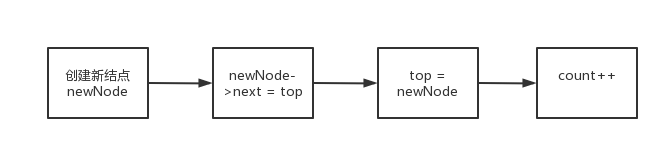
这里需要理清楚指针与结点之间的关系。指针是指向存储空间而不是存储空间,通过指针能访问存储空间。这里的top是个指针他始终指向栈顶元素,存储的是栈顶元素的首地址。因此通过top能访问栈顶元素。插入一个新结点在栈顶那么就需要将top指针指向该新结点,并将原先的栈顶结点作为新结点的下一个结点。
error_code get_pop(T& x)
取栈顶元素并将其存储在x中,这个操作不是很难
template<class T>
error_code Linked_stack<T>::get_pop(T& x)
{
if(empty())
{
return fail;
}
else{
x = top->data;
return success;
}
}
error_code pop()
删除栈顶元素
template<class T>
error_code Linked_stack<T>::pop()
{
if(empty())
{
return fail;
}
else{
LinkNode<T>* temp = top;
top = top->next;
delete temp;
count--;
}
}
此处首先判断栈是否为空,然后进行删除操作。删除栈顶元素,即删除栈顶结点并以其后继结点作为栈顶结点,那么需要声明一个临时变量储存未删除前的栈顶地址,然后再进行删除操作。
int get_size()
非常简单直接上代码
template<class T>
int Linked_stack<T>::get_size()
{
return count;
}
void clear()
也非常简单
template<class T>
void Linked_stack<T>::clear()
{
while(!empty())
{
pop();
}
}
完整代码
#ifndef LINKED_STACK_H
#define LINKED_STACK_H
#include "LinkNode.h"
#include<iostream>
// g++编译器不支持将模板文件分离编译因此需要将模板函数的实现写在类定义的头文件内
using namespace std;
enum error_code{
success,
fail
};
template <class T>
class Linked_stack{
public:
Linked_stack(){
count = 0;
top = NULL;
}; // 初始默认构造函数
Linked_stack(T *value,int n); // 传入数组根据数组建立栈
~Linked_stack(); // 析构函数
public:
error_code push(T x); // 将新元素压入栈
error_code pop(); // 栈顶元素出栈,并将该值保存到x中
error_code get_pop(T& x); // 获取栈顶元素,并将该值保存到x
bool empty(); // 栈是否为空
int get_size(); // 获取当前栈元素个数
void clear(); // 清空栈内容
private:
LinkNode<T> *top; // 栈顶指针
int count; // 记录栈内元素个数
};
#endif
#include<iostream>
using namespace std;
// 构造函数
template <class T>
Linked_stack<T>::Linked_stack(T *value,int n){
count = 0;
for(int i=0;i<n;i++){
push(value[i]);
count++;
}
}
template <class T>
Linked_stack<T>::~Linked_stack(){
clear();
}
// 栈顶元素出栈并将该元素的值保存至x
template <class T>
error_code Linked_stack<T>::pop(){
// 首先判断栈是否为空
if(empty() == true){
return fail;
}
else{
int x;
LinkNode<T> *currentNode = top;
top = top->next;
x = currentNode->data;
delete currentNode;
count--;
return success;
}
}
// 新元素入栈
template <class T>
error_code Linked_stack<T>::push(T x){
LinkNode<T> *newNode = new LinkNode<T>();
if(newNode == NULL){
return fail;
}
newNode->next = top;
newNode->data = x;
top = newNode;
count++;
return success;
}
//获取栈顶元素
template <class T>
error_code Linked_stack<T>::get_pop(T &x){
// 首先判断栈是否为空
if(empty() == true){
return fail;
}
else{
x = top->data;
return success;
}
}
template <class T>
bool Linked_stack<T>::empty(){
if(count == 0)
return true;
return false;
}
template <class T>
int Linked_stack<T>::get_size(){
return count;
}
template <class T>
void Linked_stack<T>::clear(){
LinkNode<T> *curNode = NULL;
while(top != NULL){
curNode = top;
top = top->next;
delete curNode;
}
count = 0;
}
这里有一个小细节就是使用模板类的话,类中函数的实现要写在头文件内,不然g++编译器无法找到类中函数的实现。
链式队列
存储结构
队头队尾位置的确定
首先要明确,队列的插入即入队操作是在尾部进行,而插入操作需要知道当前链表的尾结点从而向其插入元素。队列的删除即出队操作是在头部进行,因而设置在链表头。
头指针front与尾指针rear的初始化与指向
此处分为两种初始化情况对应还是有一定的差别的
- front,rear初始化为NULL
此时在添加结点时会出现两种情况
1.当前添加的结点是队列元素的首结点
此时在向队列中添加结点时,front和rear都应该指向该结点
2.当前添加的结点不是队列元素的首结点
此时front不应改变,只需使rear指针指向新添加的结点
此时会发现添加结点会对应两种不同的操作,那么我们需要在添加结点的时候进行一个逻辑判断,来判断其是否为首个结点,会带来些许不便但也是可以的 - 初始化一个不储存任何值的头结点,front和rear分别指向该节点
此时在进行插入操作时便只需要改变尾结点的指向,无论队列中的元素数量如何。此时要注意在写析构函数的时候别忘记释放头结点的存储空间
链式队列的结构描述
链结点代码
#ifndef LINK_NODE_H
#define LINK_NODE_H
// 队列结点类的定义
#include<iostream>
template<class T>
struct Node{
T data;
Node<T> *next;
Node(Node<T>* ptr = NULL){
next = ptr;
}
Node(T value){
data = value;
next = NULL;
}
};
#endif
函数代码实现及设计思路
Linked_queue()
这里如上面所说有两种设计此处分别给出
- front与rear同时初始化为NULL
template<class T>
Linked_queue<T>::Linked_queue(){
front = NULL;
rear = NULL;
count = 0;
}
- 建立一个头结点
template<class T>
Linked_queue<T>::Linked_queue(){
Node<T>* head = new Node<T>();
front = head;
rear = head;
count = 0;
}
~Linked_queue()
析构函数由于有两种不同的初始化方式,那么此时析构函数也对应两种不同的操作
- front与rear同时初始化为NULL
template<class T>
Linkde_queue<T>::~Linked_queue()
{
while(!empty())
{
serve(); 删除元素
}
}
- 建立一个头结点
Linkde_queue<T>::~Linked_queue()
{
while(!empty())
{
serve();
}
delete front; // 删除头结点
}
bool empty()
判断队列是否为空,此处根据count是否为零判断即可,也可以根据front是否与rear相等来判断
template<class T>
bool Linked_queue<T>::empty()
{
return count == 0;
}
error_code get_front(T& x)
- 初始化时front与rear为NULL
template<class T>
error_code Linked_queue<T>::get_front(T& x)
{
if(empty())
{
return fail;
}
x = front->data;
return success;
}
- 初始化带有头结点
template<class T>
error_code Linked_queue<T>::get_front(T& x)
{
if(empty())
{
return fail;
}
x = front->next->data;
return success;
}
error_code append(T x)
向队列中添加元素,那么此时更分成两种情况,一种为不含头结点一种为含头结点
- 初始化时front与rear为NULL
template<class T>
error_code Linked_queue<T>::append(T x)
{
// 需要加一个判断对于队列为空的情况
if(empty())
{
Node<T>* newNode = new Node<T>(x);
newNode->next = NULL;
front = newNode;
rear = newNode;
count++;
return success;
}
Node<T>* newNode = new Node<T>(x);
newNode->next = NULL;
rear->next = newNode; // 连接
rear = newNode;
count++;
return success;
}
- 带有头结点
template<class T>
error_code Linked_queue<T>::append(T x)
{
Node<T>* newNode = new Node<T>(x);
newNode->next = NULL;
rear->next = newNode; // 连接
rear = newNode;
count++;
return success;
}
error_code get_rear(T& x)
获取队列尾部元素
template<class T>
error_code Linked_queue<T>::get_rear(T& x)
{
if(empty())
{
return fail;
}
x = rear->data;
return success;
}
队头元素出队
删除队头元素这里也要分为两种情况进行讨论
- 初始化时front与rear为NULL
此时front指针指向的就是队列的第一个结点
template<class T>
error_code Linked_queue<T>::serve()
{
if(empty())
{
return fail;
}
Node<T>* temp = front;
front = front->next;
delete temp;
count--;
return success;
}
- 有头结点
此时front指向的就不再是第一个元素而是头结点,front-next才为第一个元素,并且此时要注意一个极端情况就是删除的队列中只有一个结点时,此时要将rear也只为头结点
template<class T>
error_code Linked_queue<T>::serve()
{
if(empty())
{
return fail;
}
Node<T>* temp = front->next;
front->next = temp->next;
delete temp;
count--;
if(front->next==NULL)
{
rear = front; // 此时队列中无元素,如果不这样的话rear指向的存储空间已经删除,rear将无意义
}
return success;
}

