【蓝桥杯准备打卡-基础算法笔记DP篇】-1.【01背包】

1.题目介绍

有 N件物品和一个容量为 V 的背包，每件物品有各自的价值且只能被选择一次，要求在有限的背包容量下，装入的物品总价值最大。

「0-1 背包」是较为简单的动态规划问题，也是其余背包问题的基础。

动态规划是不断决策求最优解的过程

2.知识点概念介绍

2.1 DP问题的解决思路

DP问题可以被转化成 状态表示和状态计算两方面去考虑，其中、

**状态表示f[i][j] 又可以表示成 ****集合****和 ****属性**两方面，所谓 集合 是指 f[i][j]所包含的**条件**限制下所有的选法，而 该 集合的属性，指的是 这所有选法中 所表示特殊意义的值，比如最大值，最小值等等。

状态计算 则是 集合的划分方式，本质上也就是** 动态转移方程**

**集合划分的原则 **

Ⅰ.不重复 （求最大值可以忽略，但是属性为求方案数量不可忽律）

Ⅱ.不遗漏

2.2 01背包问题的解决思路

01背包问题状态表示

以 01 背包问题 为例，所谓「0-1 背包」即是不断对第 i 个物品的做出决策，「0-1」正好代表不选与选两种决定。

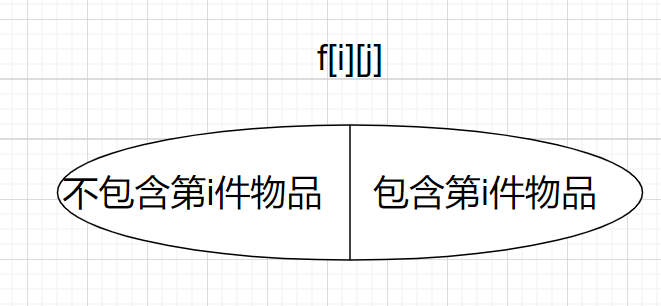
那么「0-1 背包」问题中，我们规定 f[i][j] 索表示的 集合限制 为体积j和 数目i，属性 为 价值最大值max 则f[i][j]则表示为 在前i种物品中任意选择物品 装入背包，背包总体积 不超过 j体积的 所有选法 中 价值的最大值,

易知** f[N][V] 就是我们所需要的题目答案**

01背包问题状态计算

集合的划分： 我们可以把集合f[i][j] 在前i种物品中任意选择物品 装入背包，背包总体积 不超过 j体积的 所有选法 划分为 两部分 ，一部分 包含第 i件 物品 ，另一部分 不包含第 i件物品

子集 不包含第i件物品 可以 理解为 从 1~i-1 物品中，选取的体积不超过 j 的选法集合

可以根据我们的f定义 表示为 f[i-1][j]

子集 包含第i 件物品，可以 理解成 第 i 件 物品 必然选择， 然后我们再 从 1~i-1 物品中继续，选取的体积不超过 j 的选法集合 ，但是这样显然 无法 表示成f

我们采取 “曲线救国” 的方式 ，子集 包含第i 件物品，那么我们同时 删去 该子集中 的第i 件物品，此时的 集合可以表示为 从 1~i-1 物品中继续，选取的体积不超过 j -v[i]，（v[i]表示第i个物品的体积）的选法集合，也就是f[i-1][j-v[i]] i，而 我们说过 f集合的属性是 最大的总价值， 那么这两个集合的 属性差距 ，就是第i个物品的价值，所以 该原 子集 的值 可以表示成 f[i-1][j-v[i]] +w[i]

动态转移方程：既然f 表示的是所有选法的价值最大值，那么他的值自然可以表示，他所有子集 的值 中的最大值

也就是 **f[i]][j] = max( f[ i -1] [ j ] , f[ i - 1 ][ j - v[i] ]+w[i] ) **

**值得一提的是，这里的 j 显然要大于 v【i】才有意义，不然如果 第 i 件物品的体积 比 j 大，那么图中 右侧 的子集则必然是 空集 **

3.题解代码及优化方案

3.1原始代码

#include

using namespace std;

const int MAXN = 1005;
int v[MAXN];    // 体积
int w[MAXN];    // 价值 
int f[MAXN][MAXN];  // f[i][j], j体积下前i个物品的最大价值 

int main() 
{
    int n, m;   
    cin >> n >> m;
    for(int i = 1; i <= n; i++) 
        cin >> v[i] >> w[i];

    for(int i = 1; i <= n; i++) 
        for(int j = 1; j <= m; j++)
        {
            //  当前背包容量装不进第i个物品，则价值等于前i-1个物品
            if(j < v[i]) 
                f[i][j] = f[i - 1][j];
            // 能装，需进行决策是否选择第i个物品
            else    
                f[i][j] = max(f[i - 1][j], f[i - 1][j - v[i]] + w[i]);
        }           

    cout << f[n][m] << endl;

    return 0;
}
/*作者：深蓝
链接：https://www.acwing.com/solution/content/1374/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。
*/

3.2 dp问题的优化思想

dp问题 的优化，无外乎 两种 ，一种是dp动态转移方程的化简 ，第二种是** dp代码化简**

两者几乎都是从 空间的优化

dp代码的化简 一般可以采取 滚动数组 的 方式 ，滚动数组 又分为 交替滚动 和 自我滚动，我们这里采用最优的自我滚动。

01 背包的优化思想

Ⅰ 转移方程的优化

 for(int j = 1; j <= m; j++)
        {
            //  当前背包容量装不进第i个物品，则价值等于前i-1个物品
            if(j < v[i]) 
                f[i][j] = f[i - 1][j];
            // 能装，需进行决策是否选择第i个物品
            else    
                f[i][j] = max(f[i - 1][j], f[i - 1][j - v[i]] + w[i]);
        }       

代码中 转移方程 f[i][j] = f[i - 1][j]和f[i][j] = max(f[i - 1][j], f[i - 1][j - v[i]] + w[i]) 我们仔细 观察，发现 方程f[i]的情况 仅仅 只 与 f[i-1]有关

对于每次循环的下一组i，只会用到i-1来更新当前值，不会用到i-2及之前值。于是可以在这次更新的时候，将原来的更新掉，反正以后也用不到。

所以对于i的更新，只需用一个数组，直接覆盖就行了。

那么 既然 每次跟新状态所需要用到的集合 只含有上一次的（而不是上两次，上三次），就可以只用一个 一维数组去记录 数值了。 即f[j] = max([j], f[j - v[i]] + w[i])

 for(int j = 1; j <= m; j++)
        {
            //  当前背包容量装不进第i个物品，则价值等于前i-1个物品
            if(j < v[i]) 
                f[j] = f[j];
            // 能装，需进行决策是否选择第i个物品
            else    
                f[j] = max(f[j], f[j - v[i]] + w[i]);
        }       

Ⅱ 循环代码的优化

这段代码根据 我们可以加入 第二重循环的条件里，直接从 j = f【j】作为循环初值，就可以去除 if语句，两者等价

 for(int j = v[i]; j <= m; j++)
        {
            // 能装，需进行决策是否选择第i个物品   
                f[j] = max(f[j], f[j - v[i]] + w[i]);
        }       

Ⅲ 循环代码的 逆序

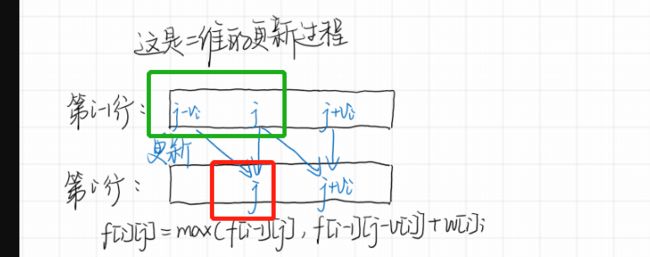
在二维情况下，状态f[i][j]是由上一轮i - 1的状态得来的，f[i][j]与f[i - 1][j]是独立的。而优化到一维后，如果我们还是正序，则有f[较小体积]更新到f[较大体积]，则有可能本应该用第i-1轮的状态却用的是第i轮的状态。

例如，一维状态第i轮对体积为 3 的物品进行决策，则f[7]由f[4]更新而来，这里的f[4]正确应该是f[i - 1][4]，但从小到大枚举j这里的f[4]在第i轮计算却变成了f[i][4]。当逆序枚举背包容量j时，我们求f[7]同样由f[4]更新，但由于是逆序，这里的f[4]还没有在第i轮计算，所以此时实际计算的f[4]仍然是f[i - 1][4]。

简单来说，一维情况正序更新状态f[j]需要用到前面计算的状态已经被「污染」，逆序则不会有这样的问题。

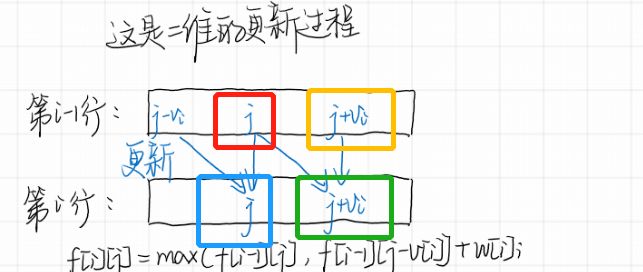
你看如果是是正序优化循环，那么 ** 红框** 的 值 也就是从 绿框 中 选最大的 跟新，而 下图中绿色框处的值本来应该是 红黄两框中 的最大值，正序循环一维化 中，则变成了从蓝框 和黄框 中的 最大值了，如果蓝框和红框 的内容不一致， 则 会导致 绿框 处 值跟新错误 ，而如果我们从 第i行的最后一列开始跟新状态即 逆序跟新 则不会出现这样的情况

下图是acwing 中大佬理解图，觉得不错偷过来

Ⅳ 输入数值的优化

我们注意到在处理数据时，我们是一个物品一个物品，一个一个体积的枚举。

因此我们可以不必开两个数组记录体积和价值，而是边输入边处理。

Ⅴ 最终代码

#include

using namespace std;

const int MAXN = 1005;
int f[MAXN];  // 

int main() 
{
    int n, m;   
    cin >> n >> m;

    for(int i = 1; i <= n; i++) {
        int v, w;
        cin >> v >> w;      // 边输入边处理
        for(int j = m; j >= v; j--)
            f[j] = max(f[j], f[j - v] + w);
    }

    cout << f[m] << endl;

    return 0;
}

4.dp问题初始值的解释

该问题 着重的焦点 在于 dp数组 状态时候 破零

本质理解是 dp 是从 第i行 物品的选与不选去解释，如果选了，就加上vi ，一开始都是背包 体积0，价值0，必然存在体积上界j 使得 物品vi可以放入，从而背包价值 从 0 变成wi