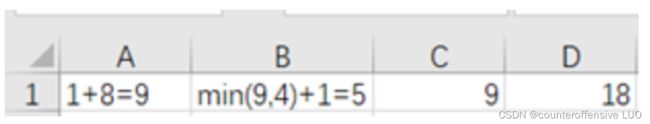整理动态规划笔记(c 和 cpp 版)
爬楼梯
一:动态规划
优化之后的程序
int climbStairs(int n) {
int p = 0, q = 0, r = 1;
for (int i = 1; i <= n; ++i) {
p = q;
q = r;
r = p + q;
}
return r;
}二:矩阵快速幂(参考力扣)
以上的方法适用于 n 比较小的情况,在 n 变大之后,O(n) 的时间复杂度会让这个算法看起来有些捉襟见肘。我们可以用「矩阵快速幂」的方法来优化这个过程
得
令
因此我们只要能快速计算矩阵 M的 n 次幂,就可以得到 f(n) 的值。如果直接求取 ,时间复杂度是 O(n) 的,我们可以定义矩阵乘法,然后用快速幂算法来加速这里
如何想到使用矩阵快速幂?
-
如果一个问题可与转化为求解一个矩阵的 n 次方的形式,那么可以用快速幂来加速计算
-
如果一个递归式形如
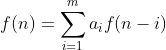 ,即齐次线性递推式,我们就可以把数列的递推关系转化为矩阵的递推关系,即构造出一个矩阵的 n 次方乘以一个列向量得到一个列向量,这个列向量中包含我们要求的 f(n) .一般情况下,形如
,即齐次线性递推式,我们就可以把数列的递推关系转化为矩阵的递推关系,即构造出一个矩阵的 n 次方乘以一个列向量得到一个列向量,这个列向量中包含我们要求的 f(n) .一般情况下,形如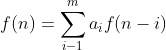 可以构造出这样的m x m 的矩阵:
可以构造出这样的m x m 的矩阵:
![]()
- 那么遇到非齐次线性递推我们是不是就束手无策了呢?其实未必。有些时候我们可以把非齐次线性递推转化为齐次线性递推,比如这样一个递推:
我们可以做这样的变换:
令x![]() ,那么我们又得到了齐次线性递推:
,那么我们又得到了齐次线性递推:
于是就可以使用矩阵快速幂求解了。当然并不是所有非齐次线性都可以化成齐次线性,我们还是要具体问题具体分析。
以下是矩阵快速幂的代码实现
struct Matrix {
long long mat[2][2];
};
struct Matrix multiply(struct Matrix a, struct Matrix b) { // 矩阵 a*b
struct Matrix c;
for (int i = 0; i < 2; i++) {
for (int j = 0; j < 2; j++) {
c.mat[i][j] = a.mat[i][0] * b.mat[0][j] + a.mat[i][1] * b.mat[1][j];
}
}
return c;
}
struct Matrix matrixPow(struct Matrix a, int n) { // a 是 f(1) f(2)
struct Matrix ret; // M
ret.mat[0][0] = ret.mat[1][1] = 1;
ret.mat[0][1] = ret.mat[1][0] = 0;
while (n > 0) {
if ((n & 1) == 1) {
ret = multiply(ret, a); // ret = ret*a
}
n >>= 1; // -->n/2
a = multiply(a, a);
}
return ret;
}
int climbStairs(int n) {
struct Matrix ret;
ret.mat[1][1] = 0;
ret.mat[0][0] = ret.mat[0][1] = ret.mat[1][0] = 1;
struct Matrix res = matrixPow(ret, n); // ret 的 n 次方
return res.mat[0][0];
}三:通项公式
之前的方法我们已经讨论了f(n)是齐次线性递推,根据递推方程![]() ,我们可以写出这样的特征方程:
,我们可以写出这样的特征方程:
求得![]() ,
,![]() 设通解为
设通解为![]() ,代入初始条件
,代入初始条件![]() ,
,![]() ,得
,得![]() ,
,![]() ,我们得到了这个递推数列的通项公式:
,我们得到了这个递推数列的通项公式:
接着我们就可以通过这个公式直接求第 n 项了
int climbStairs(int n) {
double sqrt5 = sqrt(5);
double fibn = pow((1 + sqrt5) / 2, n + 1) - pow((1 - sqrt5) / 2, n + 1);
return (int) round(fibn / sqrt5);
}总结:
-
n比较小的时候,我们直接使用过递归法求解, 不做任何记忆化操作,时间复杂度是O(2^n),存在很多冗余计算
-
一般情况下,我们使用「记忆化搜索」或者「迭代」的方法,实现这个转移方程,时间复杂度和空间复杂度都可以做到 O(n)
-
为了优化空间复杂度,我们可以不用保存 f(x - 2)之前的项,我们只用三个变量来维护 f(x)、f(x - 1)和 f(x - 2),你可以理解成是把「滚动数组思想」应用在了动态规划中,也可以理解成是一种递推,这样把空间复杂度优化到了 O(1)
-
随着 n 的不断增大 O(n) 可能已经不能满足我们的需要了,我们可以用「矩阵快速幂」的方法把算法加速到 O(logn)
-
我们也可以把 n 代入斐波那契数列的通项公式计算结果,但是如果我们用浮点数计算来实现,可能会产生精度误差
矩形盖
仔细观察是斐波拉契问题
某一次的结果可以是由一块叠来的,也可以是由两块小的叠来的
字符串问题
给定一个由0-9组成的字符串,1可以转化成A,2可以转化成B。依此类推。。25可以转化成Y,26可以转化成z,给一个字符串,返回能转化的字母串的有几种?
两种转化方法
1)字符i自己转换成自己对应的字母
2)和前面那个数组成两位数 ( 如果两位数是小于27的就可以 ),然后转换成对应的字母
矩阵问题:
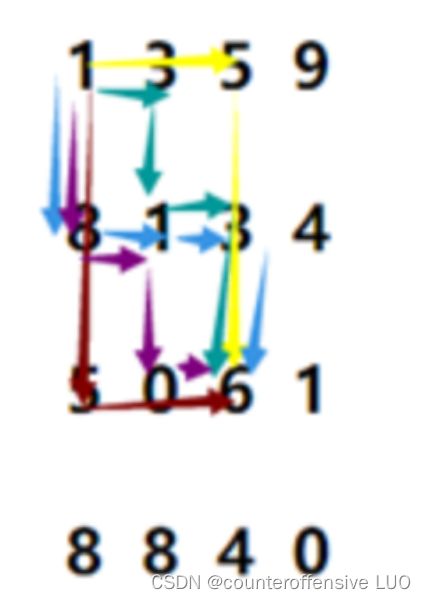
给一个由数字组成的矩阵,初始在左上角,要求每次只能向下或向右移动,路径和就是经过的数字全部加起来,求可能的最小路径和
分析:我们可以像之前一样,暴力的把每一种情况都试一次,但是依旧会造成过多的重复计算,以本题为例子最后解释一下暴力慢在哪里,以后不再叙述了
从1到6有很多路可走
将A到某个点的最小距离之和填入以下表格
优化空间复杂度(重新开辟一行空间,用来存储步数)
B:9 是 A 的(从左面走过来) ,4 是上面的(从上面走下来的), 1 是这个格子本来的
// 遍历原矩阵
// 初始化
//
#define MAX_SIZE 100
int min(int a, int b) {
return a>b?b:a;
}
int minPath(int nums[][4], int numsLine, int numsCol) {
// 按道理要分情况
int a[MAX_SIZE];
int flag = 0;
for(int i = 0; i < numsCol; ++i) {
a[i] = nums[0][i]+flag;
flag = a[i];
}
for(int i = 1; i < numsLine; ++i) {
for(int j = 0; j < numsCol; ++j){
if(j)
a[j] = min(a[j-1], a[j]);
a[j] += nums[i][j];
}
}
return a[numsCol-1];
}给一个由数字组成的矩阵,初始在左上角,要求每次只能向下或向右移动,路径和就是经过的数字全部加起来,求可能的最大路径和
- 将 min 改 max 就可以了(代码实现时将min 改为 max 即可)
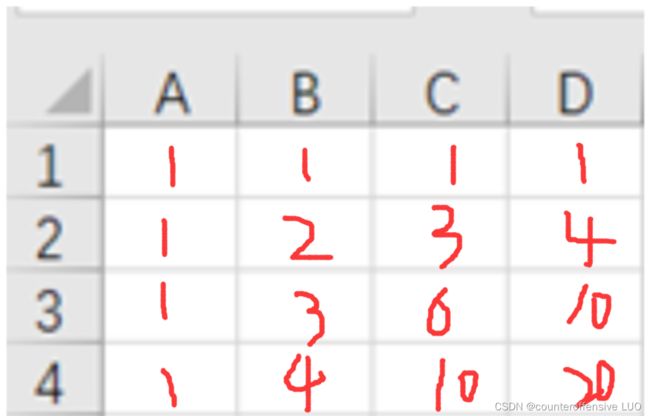
一个矩阵,初始在左上角,要求每次只能向下或向右移动,求到终点的方法数(将最大最小路径简化了,第一行第一列是1,之后用min计算即可)
代码实现如下
#define MAX_SIZE 100
int max(int a, int b) {
return a>b?a:b;
}
int minWay(int numsLine, int numsCol) {
// 按道理要分情况
int a[MAX_SIZE];
// 计算小的情况就可以了
int mAx = max(numsLine, numsCol);
int min = numsLine + numsCol - mAx;
for(int i = 0; i < min; ++i)
a[i] = 1;
for(int i = 1; i < mAx; ++i) {
for(int j = 1; j < min; ++j){
a[j] = a[j-1]+a[j];
}
}
return a[min-1];
}暗黑字符串:判断字符串纯净还是暗黑(网易17校招)
参考牛客网
刷格子(蓝桥杯)
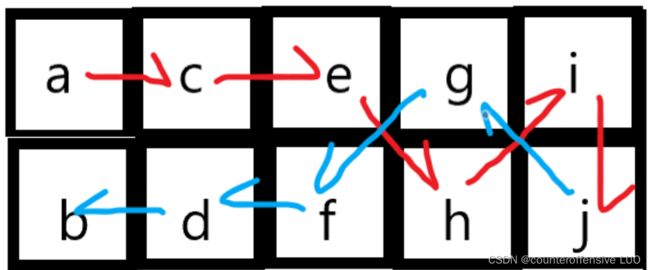
问题描述 古国的一段古城墙的顶端可以看成 2×N个格子组成的矩形(如下图所示),现需要把这些格子刷上保护漆。 例如下图是一个长度为3,高为2的城墙
![]()
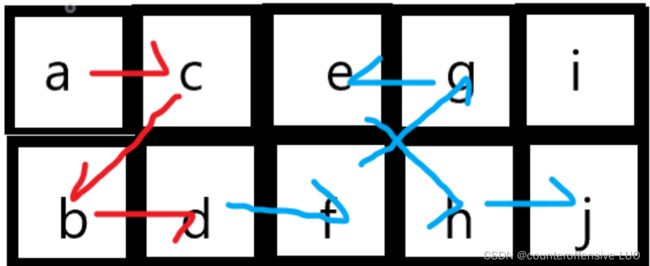
你可以从任意一个格子刷起,刷完一格,可以移动到和它相邻的格子(对角相邻也算数),但不能移动到较远的格子(因为油漆未干不能踩!) 比如: a d b c e f 就是合格的刷漆顺序。 c e f d a b 是另一种合适的方案。 当已知 N 时,求总的方案数。当n较大时,结果会迅速增大,请把结果对 1000000007 (十亿零七) 取模。
输入格式:输入数据为一个正整数(不大于1000) 输出格式:输出数据为一个正整数。
样例输入:2 样例输出:24 样例输入:3 样例输出:96 样例输入:22 样例输出:359635897
题解:
-
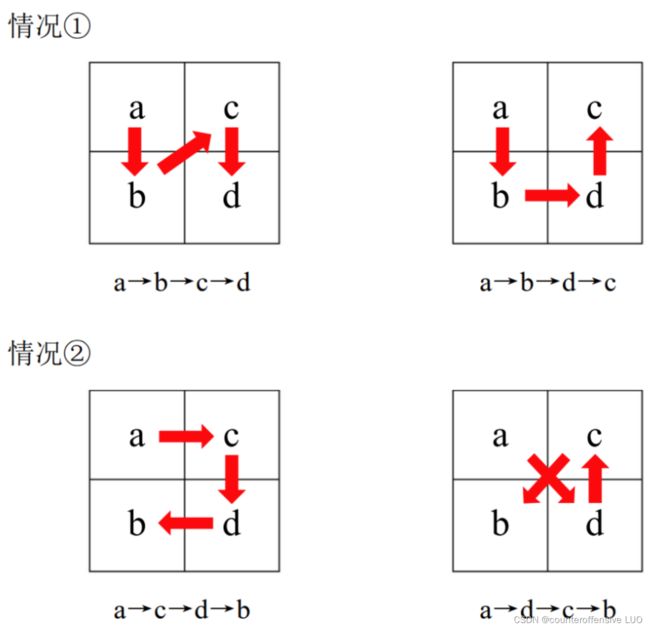
从四个顶点出发时
从中间走就必须得回到同一列继续走另一边的格子,e往左边走时,一趟去一趟回,回到 f 走另一边,另一边可以一趟走到底,也可以来回走两趟
e 和 f 有两种选择,乘2
走到左边需要回来,2b[i]
回到 f 往右边走,右边就是在顶点开始的方法,2a[n-i]
所以结果是, 2b[i]*2a[n-i] = 4 *b[i] *a[n-i]
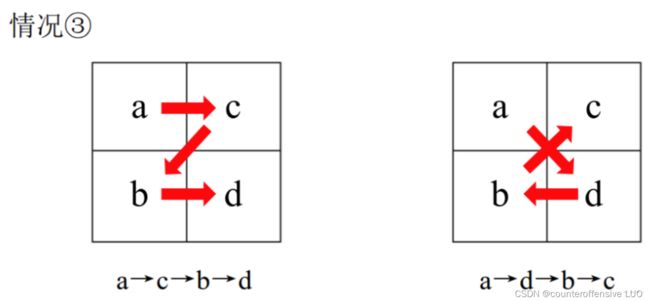
还有一种就是先往右边走再往左边走:
右边:2*b[n-i+1]
左边:2*a[i]
结果是:2*b[n-i+1] *a[i] = 4 *b[n-i+1] *a[i-1]
从中间走的所有情况是:4 * ( b[i]* a[n-i] + b[n-i+1]*a[i-1] )
所以将以上都加起来就可以得到所有结果
sum = 4* a[n] + 4 * ( b[i]* a[n-i] + b[n-i+1]*a[i-1] )
还有对部分值进行初始化
const int MOD=1000000007;
int main()
{
int n; cin>>n;
long long a[1005],b[1005];
if(n==1){
cout<<2<a数组是走完一列走下一列
和走另一列回来再走另一列的另一个
b数组是走一趟过去一趟回来
背包问题
01背包
![]()
这是最基础的背包问题,特点是:每种物品仅有一件,可以选择放或不放。
用子问题定义状态:
f[i][j]表示前i件物品恰放入一个容量为j的背包可以获得的最大价值。则其状态转移方程为:
![]()
-
如果不放第i件物品,那么问题就转化为“前i−1件物品放入容量为j的背包中”,价值为f[i−1][j];
-
如果放第i件物品,那么问题就转化为“前i−1件物品放入剩下的容量为j−c[i]的背包中”,此时能获得的最大价值就是f[i−1][j−w[i]],再加上通过放入第i件物品获得的价值v[i]
继续优化空间(利用之前提到的知识):如果我们压缩到一维空间解题
浅提动态规划
根据动态规划解题步骤(问题抽象化、建立模型、寻找约束条件、判断是否满足最优性原理、找大问题与小问题的递推关系式、填表、寻找解组成)找出01背包问题的最优解以及解组成,然后编写代码实现。
动态规划的原理 动态规划与分治法类似,都是把大问题拆分成小问题,通过寻找大问题与小问题的递推关系,解决一个个小问题,最终达到解决原问题的效果。但不同的是,分治法在子问题和子子问题等上被重复计算了很多次,而动态规划则具有记忆性,通过填写表把所有已经解决的子问题答案纪录下来,在新问题里需要用到的子问题可以直接提取,避免了重复计算,从而节约了时间,所以在问题满足最优性原理之后,用动态规划解决问题的核心就在于填表,表填写完毕,最优解也就找到。
最优性原理是动态规划的基础,最优性原理是指“多阶段决策过程的最优决策序列具有这样的性质:不论初始状态和初始决策如何,对于前面决策所造成的某一状态而言,其后各阶段的决策序列必须构成最优策略”。
解题过程:
没有装进去的很好理解,就是V(i-1,j);
装进去了怎么理解呢?
如果装进去第i件商品,那么装入之前是什么状态,肯定是V(i-1,j-w(i))。由于最优性原理(上文讲到),V(i-1,j-w(i))就是前面决策造成的一种状态,后面的决策就要构成最优策略。两种情况进行比较,得出最优。
我的理解:其实它与之前的作了更改,只是没有比较,没有说要装那个而已
| i(物品编号) | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| w(体积) | 2 | 3 | 4 | 5 |
| v(价值) | 3 | 4 | 5 | 6 |
number=4,capacity=8
![]()
#include
using namespace std;
#include
int main()
{
int w[5] = { 0 , 2 , 3 , 4 , 5 }; //商品的体积2、3、4、5
int v[5] = { 0 , 3 , 4 , 5 , 6 }; //商品的价值3、4、5、6
int bagV = 8; //背包大小
int dp[5][9] = { { 0 } }; //动态规划表
for (int i = 1; i <= 4; i++) {
for (int j = 1; j <= bagV; j++) {
if (j < w[i])
dp[i][j] = dp[i - 1][j];
else
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - w[i]] + v[i]);
}
}
//动态规划表的输出
for (int i = 0; i < 5; i++) {
for (int j = 0; j < 9; j++) {
cout << dp[i][j] << ' ';
}
cout << endl;
}
return 0;
} 这么大的空间就看放它值不值了,减去w[i]可能是好几个物品的空间,就看值不值,不值的话就不装
重点:
背包问题最优解回溯(回溯那些是最优解)
通过上面的方法可以求出背包问题的最优解,但还不知道这个最优解由哪些商品组成,故要根据最优解回溯找出解的组成,根据填表的原理可以有如下的寻解方式:
-
V(i,j)=V(i-1,j)时,说明没有选择第i 个商品,则回到V(i-1,j);
-
V(i,j)=V(i-1,j-w(i))+v(i)时,说明装了第i个商品,该商品是最优解组成的一部分,随后我们得回到装该商品之前,即回到V(i-1,j-w(i));
就拿上面的例子来说吧:
-
最优解为V(4,8)=10,而V(4,8)!=V(3,8)却有V(4,8)=V(3,8-w(4))+v(4)=V(3,3)+6=4+6=10,所以第4件商品被选中,并且回到V(3,8-w(4))=V(3,3);
-
有V(3,3)=V(2,3)=4,所以第3件商品没被选择,回到V(2,3);
-
而V(2,3)!=V(1,3)却有V(2,3)=V(1,3-w(2))+v(2)=V(1,0)+4=0+4=4,所以第2件商品被选中,并且回到V(1,3-w(2))=V(1,0);
-
有V(1,0)=V(0,0)=0,所以第1件商品没被选择。
![]()
#include
using namespace std;
#include
int w[5] = { 0 , 2 , 3 , 4 , 5 }; //商品的体积2、3、4、5
int v[5] = { 0 , 3 , 4 , 5 , 6 }; //商品的价值3、4、5、6
int bagV = 8; //背包大小
int dp[5][9] = { { 0 } }; //动态规划表
int item[5]; //最优解情况
void findMax() { //动态规划
for (int i = 1; i <= 4; i++) {
for (int j = 1; j <= bagV; j++) {
if (j < w[i])
dp[i][j] = dp[i - 1][j];
else
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - w[i]] + v[i]);
}
}
}
void findWhat(int i, int j) { //最优解情况
if (i >= 0) {
if (dp[i][j] == dp[i - 1][j]) {
item[i] = 0;
findWhat(i - 1, j);
}
else if (j - w[i] >= 0 && dp[i][j] == dp[i - 1][j - w[i]] + v[i]) {
item[i] = 1;
findWhat(i - 1, j - w[i]);
}
}
}
void print() {
for (int i = 0; i < 5; i++) { //动态规划表输出
for (int j = 0; j < 9; j++) {
cout << dp[i][j] << ' ';
}
cout << endl;
}
cout << endl;
for (int i = 0; i < 5; i++) //最优解输出
cout << item[i] << ' ';
cout << endl;
}
int main()
{
findMax();
findWhat(4, 8);
print();
return 0;
} 完全背包
问题是:每件物品的数量是无数件,放哪些可以让背包里的价值最大?
公式的推导:
还是利用01背包思想 dp(i,j-v)=max( dp(i-1,j-v) , dp(i-1,j-2v)+w,dp(i-1,j-3v)+2w , dp(i-1,j-4v)+3w,~~ ~依次类推到k , dp(i-1,j-kv)+(k-1)w) )
我们在这个方程两侧同时加上w,即可得到
dp(i,j-v)+w=max( dp(i-1,j-v)+w , dp(i-1,j-2v)+2w,dp(i-1,j-3v)+3w , dp(i-1,j-4v)+4w,~~dp(i-1,j-kv)+kw)
我们在回顾一下这个方程
dp(i,j)=max(dp(i-1,j) , dp(i-1,j-v)+w , dp(i-1,j-2v)+2w , dp(i-1,j-3v)+3w, ~~(以此类推到k) dp(i-1,j-k*v)+kw))
可以发现dp(i,j-v)+w可以替代
dp(i-1,j-v)+w , dp(i-1,j-2v)+2w , dp(i-1,j-3v)+3w,~~, dp(i-1,j-k*v)+kw
所以我们得出 完全背包的状态转移方程:dp(i,j)=max(dp(i-1,j),dp(i,j-v)+w)
状态变量:f[i][j] 表示前 i 件物品放入容量为 j 的背包的最大的价值
当前背包容量为 j , 我们要考虑第 i 件物品能否放入?是否放入?
-
当前背包容量 j < w[i],不能放入,则 f[i][j] = f[i-1][j]
-
当前背包容量 j >= w[i],能放入,但要比较代价
-
若第 i 件物品不放入,则f[i][j] = f[i-1][j]
-
若第 i 件物品放入,则f[i][j] = f[i][j-w[i]]+v[i]
- 对于前 i 件物品,背包容量为 j - w[i] 时可能已经放入了第 i 件物品,容量为 j 时还可以在放入第 i 件物品,所以用 f[i][j-w[i]] 更新 f[i][j]
-
代码实现如下:
#include
using namespace std;
int N,V;
int v[1010],val[1010];
int dp[1010][1010];
int main()
{
scanf("%d%d",&N,&V);
for(int i=1; i<=N; i++)
{
scanf("%d%d",&v[i],&val[i]);
}
for(int i=1; i<=N; i++)
for(int j=0; j<=V; j++)
{
dp[i][j]=dp[i-1][j];//继承上一个背包
if(j>=v[i])
{ //完全背包状态转移方程
dp[i][j]=max(dp[i-1][j],dp[i][j-v[i]]+val[i]);
}
}
printf("%d",dp[N][V]);
return 0;
} 完全背包的优化
#include
using namespace std;
int N,V;
int v[1010],val[1010];
int dp[1010];
int main()
{
scanf("%d%d",&N,&V);
for(int i=1; i<=N; i++)
{
scanf("%d%d",&v[i],&val[i]);
}
for(int i=1; i<=N; i++)
for(int j=0; j<=V; j++)
{
dp[j]=dp[j];//此时右边的dp[j]是上一层i-1的dp[j],然后赋值给了当前i的dp[i]
if(j>=v[i])
{
dp[j]=max(dp[j],dp[j-v[i]]+val[i]);//dp[j-v[i]],已经被算过
}
}
printf("%d",dp[V]);//输出最大体积,即最优解
return 0;
} 01背包
#include
using namespace std;
int w[105],v[105];
int dp[105][1005];
int main()
{
int t,m,res;
scanf("%d%d",&t,&m);
for(int i=1;i<=m;i++)
{
scanf("%d%d",&w[i],&v[i]);
}
for(int i=1;i<=m;i++)
{
for(int j=t;j>=0;j--)
{
if(j>=w[i])//只有当j>当前w[i]它才有选择的权力
{
dp[i][j]=max(dp[i-1][j-w[i]]+v[i],dp[i-1][j]);
}else{
dp[i][j]=dp[i-1][j];
}
}
}
printf("%d",dp[m][t]);
return 0;
} 01背包的优化
#include
using namespace std;
int w[105],v[105];
int dp[1000];//一维优化
int main()
{
int t,m,res;
scanf("%d%d",&t,&m);
//读入数据
for(int i=1; i<=m; i++)
{
scanf("%d%d",&w[i],&v[i]);
}
for(int i=1; i<=m; i++)
for(int j=t; j>=w[i]; j--)
{
dp[j]=max(dp[j-w[i]]+v[i],dp[j]);
}
printf("%d",dp[t]);
return 0;
} 多重背包
![]()
#include
using namespace std;
int n,m;//n个种类,m代表包总体积
int v[11010],w[11010];//v代表体积,w代表价值
int dp[2010];
int main()
{
scanf("%d%d",&n,&m);
int cnt=0;//cnt统计新的种类
for(int i=1; i<=n; i++)
{
int a,b,s;//体积,价值,数量
scanf("%d%d%d",&a,&b,&s);
//将s件用二进制转换为log2s堆
for(int k=1; k<=s; k<<=1)
{
v[++cnt]=k*a;//前++,第1种,第二种.....
w[cnt]=k*b;
s-=k;
}
if(s)//s有剩余,自立为新品种
{
v[++cnt]=s*a;
w[cnt]=s*b;
}
}
//01背包做法
for(int i=1; i<=cnt; i++)
{
for(int j=m; j>=v[i]; j--)
{
dp[j]=max(dp[j],dp[j-v[i]]+w[i]);//动态转移方程和01背包完全相同
}
}
printf("%d",dp[m]);
return 0;
} 有的图或代码借鉴优秀博主,感谢csdn博主