MATLAB二值图连通域快速标记算法

by HPC_ZY

---

由于工程需要，用C++实现三维二值图像的连通域标记。像往常一样拿起冈萨雷斯《数字图像处理（第三版）》，按照算法原理先实现二维再改成三维。用（256,256,256）数据测试，根本停不下来（尴尬）。因此明白一个道理，在一定程度上 “经典” = “效率低” = “不考虑时间复杂度和空间复杂度”……
故上网查阅资料，学习快速算法，并记录在此分享给大家。

---

基本原理

连通域标记的本质就是把所有块找出来，并设置不同的编号。
循环使用区域生长即可达成目的。
主要步骤：
1）遍历图像找到种子点
2）区域生长找到区域Ni
3）记录，并在原图中删去区域Ni
4）重复1~3直至原图没有值为1的像素
参考文献《一种二值图像连通区域标记的简单快速算法》-葛春平

---

算法实现

有条件的同学请直接调用MATLAB自带的bwlabel，又快又准！
有条件的同学请直接调用MATLAB自带的bwlabel，又快又准！
有条件的同学请直接调用MATLAB自带的bwlabel，又快又准！

0. 变量解释

[M,N] = size(bw); 	   	% 二值图像与尺寸
label = zeros(M,N);        	% 标记结果
class = 0;                 	% 类别
stopflag = 0;              	% 停止标记
sp = 1;                    	% 遍历起始点
stack = zeros(M*N,2,'uint32');  % 缓存栈
stackidx = 0;			% 栈索引
neib = [-1,0;0,-1;1,0;0,1];	% 邻域偏移坐标

1.种子点搜索

1. 不好的索引方式（不使用）
   两重循环，且需要利用flag才能退出外层循环

%%%%%%%%%%%%%%%%%%%% 不使用以下代码 %%%%%%%%%%%%%%%%%%%
flag = 0;
for i = 1:M
    for j = 1:N
	if bw(i,j)
	    x = i;
	    y = j;
	    flag = 1;
	    break
	end
    end
    if flag
        break
    end
end

2. 好的索引方式，不好的搜索方式（不使用）
   利用单层循环，通过计算获得二维坐标。反复测试可提速2~4倍。

%%%%%%%%%%%%%%%%%%%% 不使用以下代码 %%%%%%%%%%%%%%%%%%%
for k = 1:M*N
    if bw(k)
        y = ceil(k/M);
        x = k-(y-1)*M;
        break
    end
end

3. 好的搜索方式
   显而易见，已经搜索过的地方不可能再出现种子点。
   连通域越多，重复次数就越多，如果每次都从（1,1）开始搜索则浪费时间。
   因此我们每次迭代都从上一种子点之后开始搜索，时间复杂度为O(n)。

sp = 1;
for k = sp:M*N
    if bw(k)
        y2 = ceil(k/M);
        x2 = k-(y2-1)*M;
        sp = k+1;
        break
    end
end

2 区域生长

方法很多，这里不做对比。我们用空间换时间，牺牲内存消耗来减少时间开销。
方法如下：
1）建立一个大小为NUM2数组stack 来保存等待生长的点的坐标（NUM的值有图像大小决定，我取的MN），并设置一个索引记录当前缓存点的个数stackidx；
2）找到种子点，放在数组第一行，并令stackidx加1；
3）对stack中第stackidx行的点进行四领域生长，在stack中删去stackidx行的点，同时stackidx减1；然后将新得到的点加入stack，同时stackidx加1。
注意：每次找到目标点都要在原图中置0,并在结果图中标号。

neib = [-1,0;0,-1;1,0;0,1];
stackidx = 0；
while stackidx
     x = stack(stackidx,1);
     y = stack(stackidx,2);
     stackidx = stackidx-1;
     for n = 1:4
            dx = x+neib(n,1);
            dy = y+neib(n,2);
            if bw(dx,dy)
                stackidx = stackidx+1;
                stack(stackidx,:) = [dx,dy];
                bw(dx,dy) = 0;
                label(dx,dy) = class;
            end
        end
end

---

完整代码

function label = label2d(bw)
[M,N] = size(bw);
label = zeros(M,N);        	 % 分类结果
class = 0;                 	 % 类别
stopflag = 0;               	 % 停止标记
sp = 1;                    	 % 遍历起始点
stack = zeros(M*N,2,'uint32');   % 缓存栈
stackidx = 0;			 % 栈索引
neib = [-1,0;0,-1;1,0;0,1];      % 邻域偏移坐标

while 1
    % 寻找种子点
    for k = sp:M*N
        if bw(k)
            y = ceil(k/M);
            x = k-(y-1)*M;
            stackidx = stackidx+1;
            stack(stackidx,:) = [x,y];
            class = class+1;
            label(x,y) = class;
            bw(x,y) = 0;
            sp = k+1;
            break
        end
        if k == M*N % 达到图像末端
            stopflag = 1;
        end
    end
    % 结束
    if stopflag
        break
    end
    % 连通域
    while stackidx
        x = stack(stackidx,1);
        y = stack(stackidx,2);
        stackidx = stackidx-1;
        for n = 1:4
            dx = x+neib(n,1);
            dy = y+neib(n,2);
            if bw(dx,dy)
                stackidx = stackidx+1;
                stack(stackidx,:) = [dx,dy];
                bw(dx,dy) = 0;
                label(dx,dy) = class;
            end
        end
    end
end
end

---

实验

对于连通域标记，MATLAB有库函数

% CC输出，BW二值图，CONN连通方式
CC = BWCONNCOMP(BW,CONN)； 

其输出为一结构体，内容分别为：连通方式，图像尺寸，连通域数量，像素索引列表。要获得标记图像还需进行操作，在下面测试中演示：

load bw2

% 库函数
tic
label1tmp = bwconncomp(bw2,4);
label1 = zeros(size(bw2));
for k = 1:label1tmp.NumObjects
    label1(label1tmp.PixelIdxList{k}) = k;  
end
t1 = toc;

% 自函数
tic
label2 = label2d(bw2);
t2 = toc;

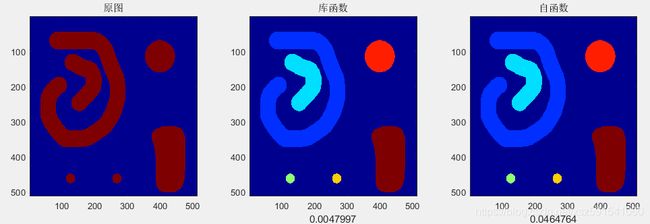
figure
subplot(131),imagesc(bw2),title('原图')
subplot(132),imagesc(label1),title('库函数'),xlabel(t1)
subplot(133),imagesc(label2),title('自函数'),xlabel(t2)
colormap jet

通过实验结果可以看出，两者输出完全一致，库函数在速度上还是更胜一筹。但相比于教材上的经典算法，自函数速度已经提升百倍以上，尤其是在三维数据上（不做测试）。

---

其他

1. 在种子点搜索和四邻域判断中，都使用了单层循环代替双层循环，以提高了计算速度。（对于三维图像效果更明显）
2. 三维连通域标记只是从二维数组变为三维数组，比较简单，大家可在上述代码基础上加入第三维（z）即可。
3. 由于C语言与MATLAB在数组存储上行列相反，所以改写为C语言时种子点搜索中坐标x,y要互换。

关于文中代码有任何问题欢迎讨论，最后还是把测试代码上传
https://download.csdn.net/download/xsz591541060/11877360
（包含二维、三维MATLAB版本以及测试代码）