zyw2002
zyw2002

经典卷积神经网络详解（AlexNet、VGG、NiN、GoogLeNet、ResNet、DenseNet、CSPNet、Darknet、EfficientNet、SqueezeNet..）

文章目录

  • 经典网络
    • LeNet : 基础图像识别网络 (1998)
    • AlexNet：深度卷积网络 （2012）
    • ZFNet ： 大型卷积网络 (2013)
    • VGGNet：使用块的网络 (2014)
    • NiN： 网络中的网络 （2014）
    • GoogLeNet : 含并行连接的网络 (2014)
    • ResNet: 残差网络 （2015）
    • DenseNet: 稠密连接网络 （2017）
    • Darknet-19 （2016）
    • Darknet-53 （2018）
    • EfficientNetV1 (2019）
    • EfficientNetV2 (2021)
    • CSPNet：跨阶段局部网络（2020）
  • 轻量化网络
    • SqueezeNet （2016）
    • MobileNetv1/2/3（2017,2018,2019）
    • ShffleNet （2017）
    • Xception （2017）
    • GhostNet(2020)
  • 参考

经典网络

LeNet : 基础图像识别网络 (1998)

LeNet概述

Paper : Gradient-Based Learning Applied to Document Recognition
Code: Deci-AI/super-gradients

LeNet-5是Yann LeCun等人在多次研究后提出的最终卷积神经网络结构，一般LeNet即指代LeNet-5。LeNet-5是用来处理手写字符的识别问题的。LeNet-5阐述了图像中像素特征之间的相关性能够由参数共享的卷积操作所提取，同时使用卷积、下采样（池化）和非线性映射这样的组合结构，是当前流行的大多是深度图像识别网络的基础。

LeNet的网络结构
经典卷积神经网络详解（AlexNet、VGG、NiN、GoogLeNet、ResNet、DenseNet、CSPNet、Darknet、EfficientNet、SqueezeNet..）_第1张图片
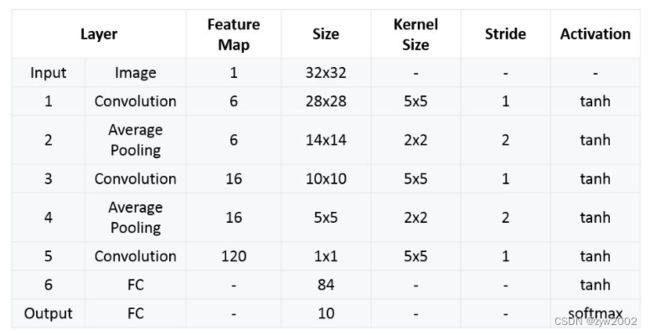
LeNet-5包含七层，不包括输入，每一层都包含可训练参数（权重），当时使用的输入数据是32*32像素的图像。下面逐层介绍LeNet-5的结构，并且，卷积层将用Cx表示，子采样层则被标记为Sx，完全连接层被标记为Fx，其中x是层索引。
LeNet-5结构：

  • 输入：32x32的灰度图像，也就是一个通道，那么一个图像就是一个2维的矩阵，没有RGB三个通道。

  • Layer1：6个大小为5x5的卷积核，步长为1。因此，到这里的输出变成了28x28x6。

  • Layer2：2x2大小的池化层，使用的是average pooling，步长为2。那么这一层的输出就是14x14x6。

  • Layer3：16个大小为5x5的卷积核，步长为1。但是，这一层16个卷积核中只有10个和前面的6层相连接。也就是说，这16个卷积核并不是扫描前一层所有的6个通道。如下图，0 1 2 3 4 5这 6个卷积核是扫描3个相邻，然后是6 7 8这3个卷积核是扫描4个相邻，9 10 11 12 13 14这6个是扫描4个非相邻，最后一个15扫描6个。实际上前面的6通道每个都只有10个卷积核扫描到。
    经典卷积神经网络详解（AlexNet、VGG、NiN、GoogLeNet、ResNet、DenseNet、CSPNet、Darknet、EfficientNet、SqueezeNet..）_第2张图片
    这么做的原因是打破图像的对称性，并减少连接的数量。如果不这样做的话，每一个卷积核扫描一层之后是10x10，一个核大小是5x5，输入6个通道，输出16个，所以是10x10x5x5x6x16=240000个连接。但实际上只有156000连接。训练参数的数量从2400变成了1516个。

  • Layer4：和第二层一样，2x2大小的池化层，使用的是average pooling，步长为2。

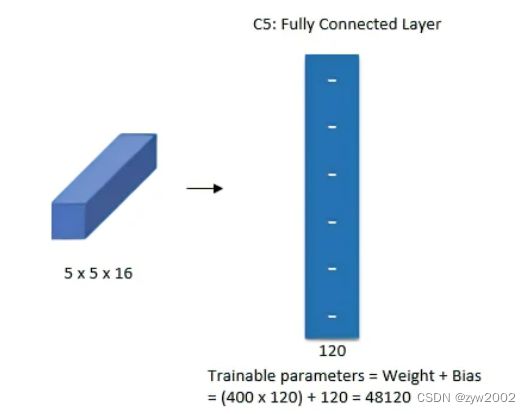
  • Layer5：全连接卷积层，120个卷积核，大小为1x1。
    第四层结束输出为16x5x5，相当于这里16x5x5展开为400个特征，然后使用120神经元去做全连接，如下图所示：
    经典卷积神经网络详解（AlexNet、VGG、NiN、GoogLeNet、ResNet、DenseNet、CSPNet、Darknet、EfficientNet、SqueezeNet..）_第3张图片

  • Layer6：全连接层，隐藏单元是84个。

  • Layer7：输出层，输出单元是10个，因为数字识别是0-9。

最终，LeNet-5的总结如下：
经典卷积神经网络详解（AlexNet、VGG、NiN、GoogLeNet、ResNet、DenseNet、CSPNet、Darknet、EfficientNet、SqueezeNet..）_第4张图片

LeNet小结

  • 卷积网络使用一个3层的序列组合：卷积、下采样 (池化)、非线性映射 (LeNet-5最重要的特 性，奠定了目前深层卷积网络的基础)
  • 使用卷积提取空间特征
  • 使用映射的空间均值进行下采样
  • 使用tanh或sigmoid进行非线性映射
  • 多层神经网络 (MLP) 作为最终的分类器
  • 层间的稀疏连接矩阵以避免巨大的计算开销

AlexNet：深度卷积网络 （2012）

AlexNet 概述：

Paper : 《ImageNet Classification with Deep Convolutional Neural Networks》
Code: alexnet-pytorch

Alex Krizhevsky等人在2012年提出了首个应用于图像分类的卷积神经网络变体AlexNet。他们认为特征本身应该被学习，而且特征应该由多个共同学习的神经网络层组成，每个层都有可学习的参数。

如下图，在网络的最底层，模型学习到了一些类似于传统滤波器的特征抽取器。
经典卷积神经网络详解（AlexNet、VGG、NiN、GoogLeNet、ResNet、DenseNet、CSPNet、Darknet、EfficientNet、SqueezeNet..）_第5张图片

AlexNet的更高层建立在这些底层表示的基础上，以表示更大的特征，如眼睛、鼻子、草叶等等。而更高的层可以检测整个物体，如人、飞机、狗或飞盘。最终的隐藏神经元可以学习图像的综合表示，从而使属于不同类别的数据易于区分。
AlexNet使用GPU代替CPU进行运算，使得在可接受的时间范围内模型结构能够更加复杂，它的出现证明了深层卷积神经网络在复杂模型下的有效性。

AlexNet的网络架构：
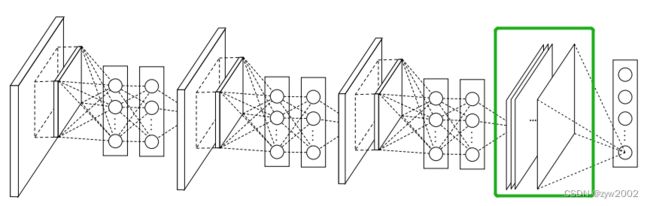
AlexNet和LeNet的架构非常相似，如下图所示。左侧是LeNet, 右侧是AlexNet。
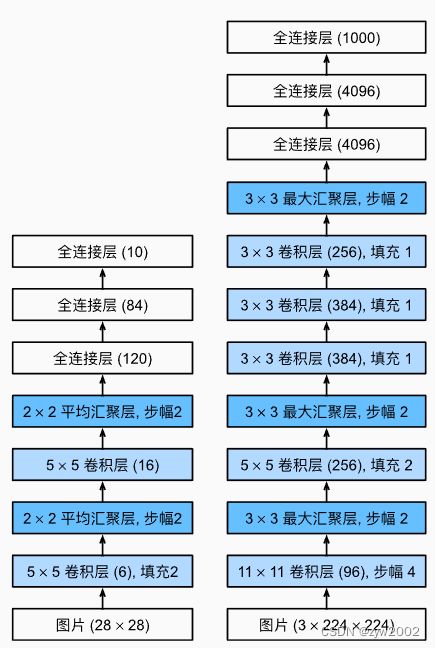
经典卷积神经网络详解（AlexNet、VGG、NiN、GoogLeNet、ResNet、DenseNet、CSPNet、Darknet、EfficientNet、SqueezeNet..）_第6张图片

AlexNet由八层组成：五个卷积层、两个全连接隐藏层和一个全连接输出层。 其次，AlexNet使用ReLU而不是sigmoid作为其激活函数。 下面，让我们深入研究AlexNet的细节。

  • 模型设计
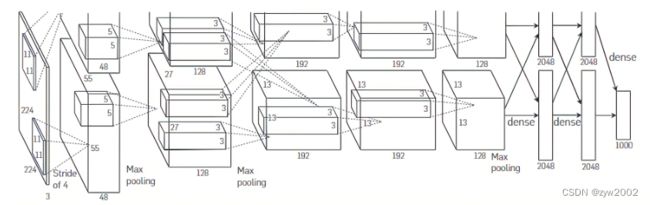
    经典卷积神经网络详解（AlexNet、VGG、NiN、GoogLeNet、ResNet、DenseNet、CSPNet、Darknet、EfficientNet、SqueezeNet..）_第7张图片
    在AlexNet的第一层，卷积窗口的形状是11×11。 由于ImageNet中大多数图像的宽和高比MNIST图像的多10倍以上，因此，需要一个更大的卷积窗口来捕获目标。 第二层中的卷积窗口形状被缩减为5×5，然后是3×3。 此外，在第一层、第二层和第五层卷积层之后，加入窗口形状为3×3、步幅为2的最大汇聚层。 而且，AlexNet的卷积通道数目是LeNet的10倍。
    在最后一个卷积层后有两个全连接层，分别有4096个输出。 这两个巨大的全连接层拥有将近1GB的模型参数。 由于早期GPU显存有限，原版的AlexNet采用了双数据流设计，使得每个GPU只负责存储和计算模型的一半参数。 幸运的是，现在GPU显存相对充裕，所以我们现在很少需要跨GPU分解模型（因此，我们的AlexNet模型在这方面与原始论文稍有不同）。

  • 最大池化
    在CNN中使用重叠的最大池化。此前CNN中普遍使用平均池化，AlexNet全部使用最大池化，避 免平均池化的模糊化效果。并且AlexNet中提出让步长比池化核的尺寸小，这样池化层的输出之间 会有重叠和覆盖，提升了特征的丰富性。

  • 激活函数
    此外，AlexNet将sigmoid激活函数改为更简单的ReLU激活函数。 一方面，ReLU激活函数的计算更简单，它不需要如sigmoid激活函数那般复杂的求幂运算。 另一方面，当使用不同的参数初始化方法时，ReLU激活函数使训练模型更加容易。 当sigmoid激活函数的输出非常接近于0或1时，这些区域的梯度几乎为0，因此反向传播无法继续更新一些模型参数。 相反，ReLU激活函数在正区间的梯度总是1。 因此，如果模型参数没有正确初始化，sigmoid函数可能在正区间内得到几乎为0的梯度，从而使模型无法得到有效的训练。
    使用ReLU作为CNN的激活函数，并验证其效果在较深的网络超过了Sigmoid，成功解决了
    Sigmoid在网络较深时的梯度弥散问题，此外，加快了训练速度，因为训练网络使用梯度下降 法，非饱和的非线性函数训练速度快于饱和的非线性函数。虽然ReLU激活函数在很久之前就被 提出了，但是直到AlexNet的出现才将其发扬光大。

  • Dropout
    AlexNet通过暂退法（dropout）控制全连接层的模型复杂度，而LeNet只使用了权重衰减。
    Dropout虽有单独的论文论述， 但是AlexNet将其实用化，通过实践证实了它的效果。在AlexNet中主要是最后几个全连接层使用 了Dropout。

  • 数据增强
    随机地从 256 × 256 256 \times 256 256×256 的原始图像中截取 224 × 224 224 \times 224 224×224 大小的区域(以及水平翻转的镜 像)，相当于增加了 ( 256 × 224 ) 2 × 2 = 2048 (256 \times 224) 2 \times 2=2048 (256×224)2×2=2048 倍的数据量。如果没有数据增强，仅靠原始的 数据量，参数众多的CNN会陷入过拟合中，使用了数据增强后可以大大减轻过拟合，提升泛化能 力。进行预测时，则是取图片的四个角加中间共 5 个位置，并进行左右翻转，一共获得10张图 片，对他们进行预测并对10次结果求均值。

  • 使用CUDA加速深度卷积网络的训练
    利用GPU强大的并行计算能力，处理神经网络训练时大量 的矩阵运算。AlexNet使用了两块GTX580GPU进行训练，单个GTX580只有3GB显存，这限制了 可训练的网络的最大规模。因此作者将AlexNet分布在两个GPU上，在每个GPU的显存中储存一 半的神经元的参数。

AlexNet的代码实现

import torch
from torch import nn
from d2l import torch as d2l

net = nn.Sequential(
    # 这里，我们使用一个11*11的更大窗口来捕捉对象。
    # 同时，步幅为4，以减少输出的高度和宽度。
    # 另外，输出通道的数目远大于LeNet
    nn.Conv2d(1, 96, kernel_size=11, stride=4, padding=1), nn.ReLU(),
    nn.MaxPool2d(kernel_size=3, stride=2),
    # 减小卷积窗口，使用填充为2来使得输入与输出的高和宽一致，且增大输出通道数
    nn.Conv2d(96, 256, kernel_size=5, padding=2), nn.ReLU(),
    nn.MaxPool2d(kernel_size=3, stride=2),
    # 使用三个连续的卷积层和较小的卷积窗口。
    # 除了最后的卷积层，输出通道的数量进一步增加。
    # 在前两个卷积层之后，汇聚层不用于减少输入的高度和宽度
    nn.Conv2d(256, 384, kernel_size=3, padding=1), nn.ReLU(),
    nn.Conv2d(384, 384, kernel_size=3, padding=1), nn.ReLU(),
    nn.Conv2d(384, 256, kernel_size=3, padding=1), nn.ReLU(),
    nn.MaxPool2d(kernel_size=3, stride=2),
    nn.Flatten(),
    # 这里，全连接层的输出数量是LeNet中的好几倍。使用dropout层来减轻过拟合
    nn.Linear(6400, 4096), nn.ReLU(),
    nn.Dropout(p=0.5),
    nn.Linear(4096, 4096), nn.ReLU(),
    nn.Dropout(p=0.5),
    # 最后是输出层。由于这里使用Fashion-MNIST，所以用类别数为10，而非论文中的1000
    nn.Linear(4096, 10))

我们构造一个高度和宽度都为224的单通道数据，来观察每一层输出的形状。

X = torch.randn(1, 1, 224, 224)
for layer in net:
    X=layer(X)
    print(layer.__class__.__name__,'output shape:\t',X.shape)

Conv2d output shape:         torch.Size([1, 96, 54, 54])
ReLU output shape:   torch.Size([1, 96, 54, 54])
MaxPool2d output shape:      torch.Size([1, 96, 26, 26])
Conv2d output shape:         torch.Size([1, 256, 26, 26])
ReLU output shape:   torch.Size([1, 256, 26, 26])
MaxPool2d output shape:      torch.Size([1, 256, 12, 12])
Conv2d output shape:         torch.Size([1, 384, 12, 12])
ReLU output shape:   torch.Size([1, 384, 12, 12])
Conv2d output shape:         torch.Size([1, 384, 12, 12])
ReLU output shape:   torch.Size([1, 384, 12, 12])
Conv2d output shape:         torch.Size([1, 256, 12, 12])
ReLU output shape:   torch.Size([1, 256, 12, 12])
MaxPool2d output shape:      torch.Size([1, 256, 5, 5])
Flatten output shape:        torch.Size([1, 6400])
Linear output shape:         torch.Size([1, 4096])
ReLU output shape:   torch.Size([1, 4096])
Dropout output shape:        torch.Size([1, 4096])
Linear output shape:         torch.Size([1, 4096])
ReLU output shape:   torch.Size([1, 4096])
Dropout output shape:        torch.Size([1, 4096])
Linear output shape:         torch.Size([1, 10])
  • 读取数据集
batch_size = 128
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size, resize=224)
  • 训练
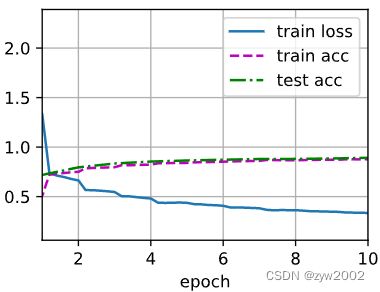
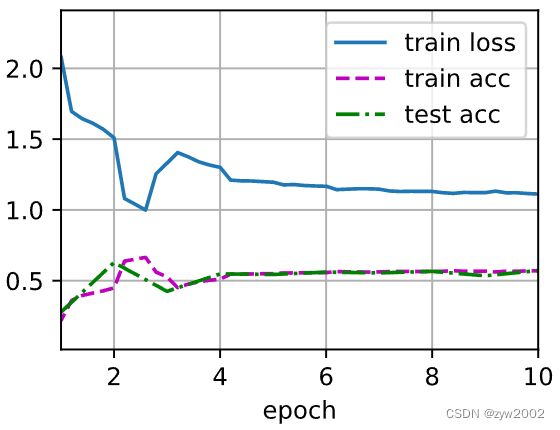
lr, num_epochs = 0.01, 10
d2l.train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())

loss 0.327, train acc 0.881, test acc 0.885
4149.6 examples/sec on cuda:0

经典卷积神经网络详解（AlexNet、VGG、NiN、GoogLeNet、ResNet、DenseNet、CSPNet、Darknet、EfficientNet、SqueezeNet..）_第8张图片

AlexNet小结：

  • 使用ReLU作为CNN的激活函数。
  • 训练时使用Dropout随机忽略一部分神经元，以避免模型过拟合。
  • 在CNN中使用重叠的最大池化。
  • 提出了LRN层，对局部神经元的活动创建竞争机制，使得其中响应比较大的值变得相对更大，并 抑制其他反馈较小的神经元，增强了模型的泛化能力。此方法在之后的VGG中被认为是无效的。
  • AlexNet在训练时增加了大量的图像增强数据，如翻转、裁切和变色。 这使得模型更健壮，更大的样本量有效地减少了过拟合。
  • 使用CUDA加速深度卷积网络的训练

ZFNet ： 大型卷积网络 (2013)

ZFNet概述

Paper :《Visualizing and Understanding Convolutional Networks 》
Code: pytorch/captum

ZFNet在2013年 ILSVRC 图像分类竞赛获得冠军，错误率11.19% ，比2012年的AlexNet降低了5%，ZFNet是由 Matthew D.Zeiler 和 Rob Fergus 在 AlexNet 基础上提出的大型卷积网络。ZFNet解释了为什么卷积神经网络可以在图像分类上表现的如此出色，以及研究了如何优化卷积神经网络。ZFNet提出了一种可视化的技术，通过可视化，我们就可以了解卷积神经网络中间层的功能和分类器的操作，这样就就可以找到较好的模型。ZFNet还进行消融实验来研究模型中的每个组件，它会对模型有什么影响。

ZFNet的网络结构
Z F N e t = (  conv  +  relu  +  maxpooling  ) × 2 + (  conv  +  relu  ) × 3 + f c × 2 +  softmax  Z F N e t=(\text { conv }+\text { relu }+\text { maxpooling }) \times 2+(\text { conv }+\text { relu }) \times 3+f c \times 2+\text { softmax } ZFNet=( conv + relu + maxpooling )×2+( conv + relu )×3+fc×2+ softmax 
ZFNet 仅仅是在 AlexNet 上做了一些调参：
改变了 AlexNet 的第一层，即将卷积核的尺寸大小 11x11 变成 7x7，并且将步长 4 变成了 2。
经典卷积神经网络详解（AlexNet、VGG、NiN、GoogLeNet、ResNet、DenseNet、CSPNet、Darknet、EfficientNet、SqueezeNet..）_第9张图片
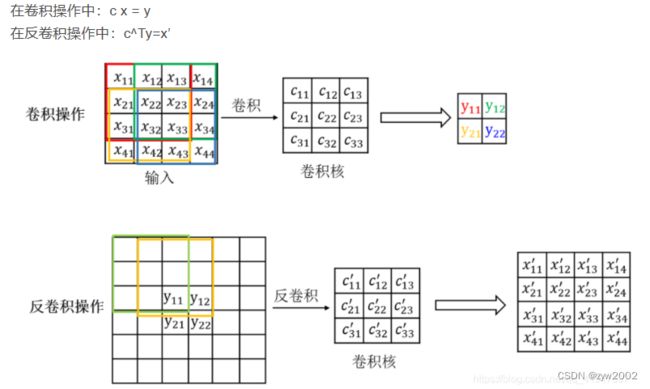
ZFNet实际上是微调（Fine-tuning）了AlexNet, 并通过反卷积（Deconvolution） 的方式可视化各层的输出特征图，进一步解释了卷积操作在大型网络中效果显著的原因。
经典卷积神经网络详解（AlexNet、VGG、NiN、GoogLeNet、ResNet、DenseNet、CSPNet、Darknet、EfficientNet、SqueezeNet..）_第10张图片

  • 对卷积结果的可视化
    作者将卷积核的计算结果（feature maps）映射回原始的像素空间（映射的方法为反卷积，反池化）并进行可视化。例如，下图Layer1区域最左上角的九宫格代表第一层卷积计算得到的前九张feature maps映射回原图像素空间后的可视化（称为f9）。第一层卷积使用96个卷积核，这意味着会得到96张feature maps，这里的前九张feature maps是指96个卷积核中值最大的9个卷积核对应生成的feature maps（这里称这9个卷积核为k9，即，第一层卷积最关注的前九种特征）。可以发现，这九种特征都是颜色和纹理特征，即蕴含语义信息少的结构性特征。
    为了证明这个观点，作者又将数据集中的原始图像裁剪成小图，将所有的小图送进网络中，得到第一层卷积计算后的feature maps。统计能使k9中每个kernel输入计算结果最大的前9张输入小图，即9*9=81张，如下图红框中右下角所示。结果表明刚刚可视化的f9和这81张小图表征的特征是相似的，且一一对应的。由此证明卷积网络在第一层提取到的是一些颜色，纹理特征。
    经典卷积神经网络详解（AlexNet、VGG、NiN、GoogLeNet、ResNet、DenseNet、CSPNet、Darknet、EfficientNet、SqueezeNet..）_第11张图片
    同理，观察Layer2和Layer3的可视化发现，第二次和第三次卷积提取到的特征蕴含的语义信息更丰富，不再是简单的颜色纹理信息，而是一些结构化的特征，例如蜂窝形状，圆形，矩形等等。那么网络的更深层呢？我们看下图：
    经典卷积神经网络详解（AlexNet、VGG、NiN、GoogLeNet、ResNet、DenseNet、CSPNet、Darknet、EfficientNet、SqueezeNet..）_第12张图片
    在网络的深层，如第四层，第五层卷积提取到的是更高级的语义信息，如人脸特征，狗头特征，鸟腿鸟喙特征等等。
    最后，越靠近输出端，能激活卷积核的输入图像相关性越少（尤其是空间相关性），例如Layer5中，最右上角的示例：feature map中表征的是一种绿色成片的特征，可是能激活这些特征的原图相关性却很低（原图是人，马，海边，公园等，语义上并不相干）；其实这种绿色成片的特征是‘草地’，而这些语义不相干的图片里都有‘草地’。‘草地’是网络深层卷积核提取的是高级语义信息，不再是低级的像素信息，空间信息等等。

  • 网络中对不同特征的学习速度
    如下图所示，横轴表示训练轮数，纵轴表示不同层的feature maps映射回像素空间后的可视化结果：
    在这里插入图片描述
    由此可以看出，low-level的特征(颜色，纹理等)在网络训练的训练前期就可以学习到， 即更容易收敛；high-level的语义特征在网络训练的后期才会逐渐学到。 由此展示了不同特征的进化过程。这也是一个合理的过程，毕竟高级的语义特征，要在低级特征的基础上学习提取才能得到。

  • 图像的平移、缩放、旋转对CNN的影响
    下图是探究图片平移对卷积模型影响的实验，a1是五张不同的图片经过不同大小的左右平移后的结果。
    a2是原始图片与经过平移后的图片分别送进卷积网络后，第一层卷积计算得到的feature maps之间的欧氏距离，可以看出当图片平移0个像素时（即图中横轴=0处），距离最小（等于0）。其他位置随着左右平移，得到的距离都会陡增或陡减。五条彩色曲线分别代表五张不同的原始图片。
    a3是原始图片与经过平移后的图片分别送进卷积网络后，第七层卷积计算得到的feature maps之间的欧氏距离，可以看出趋势与a2类似；但是，增减的曲线变换更平缓，这一定程度上说明了网络的深层提取的是高级语义特征，而不是低级的颜色，纹理，空间特征。这种语义信息不会随着平移操作而轻易改变，例如狗的图片平移后还是狗。
    这个性质叫做：卷积拥有良好的平移不变性。
    最后，a4表示的是原始图片与经过平移后的图片分别送进卷积网络后，卷积网络最后的识别结果。可以看出识别准确率是相对平稳的，且在横轴x=0时，识别准确率较高（此时，图片不平移，识别物体基本在图片中心位置）。
    经典卷积神经网络详解（AlexNet、VGG、NiN、GoogLeNet、ResNet、DenseNet、CSPNet、Darknet、EfficientNet、SqueezeNet..）_第13张图片
    下图探究图片缩放对卷积模型影响的实验，实验方法和表述与上面探讨平移时的设置类似。结果表明，网络的浅层相较于网络的深层对缩放操作更敏感；且最终的识别准确率较平稳。这个趋势跟探究平移操作对卷积模型影响的趋势类似，即：卷积操作也具有良好的缩放不变性。
    经典卷积神经网络详解（AlexNet、VGG、NiN、GoogLeNet、ResNet、DenseNet、CSPNet、Darknet、EfficientNet、SqueezeNet..）_第14张图片
    下图是探究图片旋转对卷积模型影响的实验，可以看出旋转操作对卷积的影响正好与平移和缩放相反：卷积第一层对旋转的敏感程度较低，第七层对旋转的敏感程度高。这是因为颜色，纹理这些低级特征旋转前后还是相似的特征；但是目标级别的高级语义特征却不行，例如“特征9”旋转180°后变成了“特征6”. 看最终的识别准确率曲线也能发现旋转0°和350°时模型的识别准确率最高，因为此时旋转后模型最接近原始图片。对于某些存在对称性质的特征，例如原图中的电视，在旋转90°，180°，270°时都有不错的识别准确率。因此，卷积操作不具有良好的旋转不变性。
    经典卷积神经网络详解（AlexNet、VGG、NiN、GoogLeNet、ResNet、DenseNet、CSPNet、Darknet、EfficientNet、SqueezeNet..）_第15张图片
    总结：
    卷积的平移不变性是从滑动遍历这个操作带来的，不管一个特征出现在图中的什么位置，卷积核都可以通过滑动的方式，滑动到特征上面做识别。
    卷积的缩放不变性则是从网络的层级结构中获得，不同层的卷积操作拥有不同尺寸的计算感受野 。至于旋转不变性缺失找不到对应的操作。
    那么，为什么现在的一些成熟项目，例如人脸识别，图像分类等依然可以对旋转的图片做识别呢？ 这是因为我们用大量的训练数据，旋转不变性可以从大量的训练数据中得到。其实，不仅是旋转不变性，卷积本身计算方法带来的平移不变性和缩放不变性也是脆弱的，大部分也是从数据集中学习到的。深度学习是一种基于数据驱动的算法。

  • 改变卷积核的大小
    ZFNet通过对AelxNet可视化发现，由于第一层的卷积核尺寸过大导致某些特征图失效（失效指的是一些值太大或太小的情况，容易引起网络的数值不稳定性，进而导致梯度消失或爆炸。图中的体现是（a）中的黑白像素块）。
    经典卷积神经网络详解（AlexNet、VGG、NiN、GoogLeNet、ResNet、DenseNet、CSPNet、Darknet、EfficientNet、SqueezeNet..）_第16张图片

此外，由于第一层的步长过大，导致第二层卷积结果出现棋盘状的伪影（例如（d）中第二小图和倒数第三小图）。因此ZFNet做了对应的改进。即将第一层 11X11步长为4的卷积操作变成 7X7步长为2的卷积。

  • 遮挡对卷积模型的影响
    ZFNet通过对原始图像进行矩形遮挡来探究其影响，如下图所示：
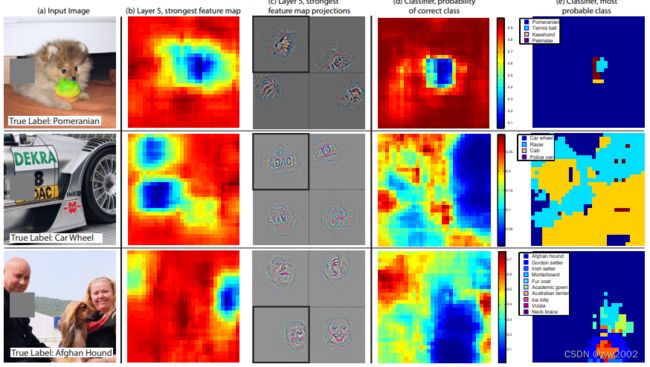
    经典卷积神经网络详解（AlexNet、VGG、NiN、GoogLeNet、ResNet、DenseNet、CSPNet、Darknet、EfficientNet、SqueezeNet..）_第17张图片
    b表示计算遮挡后的图像经过第五个卷积层后得到的feature map 值的总和。红色代表更大的值。 由此可以看出来卷积计算后的特征图也是保留了原始数据中不同类别对象在图像中的空间信息。
    c左上角的小图是经过第五个卷积后值最大的特征图的deconv可视化结果。由此实例2（可视化结果为英文字母或汉字，但原图的标签是“车轮”）可以看出卷积后值最大的特征图不一定是对分类最有作用的。c中的其他小图是统计数据集中其他图像可以使该卷积核输出最大特征图的deconv可视化结果。
    d表示灰色滑块所遮挡的位置对图像正确分类的影响，红色代表分类成功的可能性大。例如博美犬的图像，当灰色滑块遮挡到博美犬的面部时，模型对博美犬的识别准确率大幅度下降。
    e表示模型对遮挡后的图像的分类结果是什么。还拿博美犬的例子，灰色遮挡在图片中非狗脸的位置时，都不影响模型将其正确分类为博美犬（大部分都是蓝色标签，除了遮挡滑动到狗脸位置时）。
    这个遮挡实验证明，深层的网络提取的是语义信息（例如狗的类属），而不是low-level的空间特征。因此对随机遮挡可以不敏感。

ZFNet的实现代码

import torch.nn as nn
import torch 

# 与AlexNet有两处不同： 1. 第一次的卷积核变小，步幅减小。 2. 第3，4，5层的卷积核数量增加了。
class ZFNet(nn.Module):
    def __init__(self, num_classes=1000, init_weights=False):
        super(ZFNet, self).__init__()
        self.features = nn.Sequential(
            nn.Conv2d(3, 96, kernel_size=7, stride=2, padding=2),  # input[3, 224, 224]  output[96, 111, 111]
            nn.ReLU(inplace=True),
            nn.MaxPool2d(kernel_size=3, stride=2),                  # output[96, 55, 55]

            nn.Conv2d(96, 256, kernel_size=5, padding=2),           # output[256, 55, 55]
            nn.ReLU(inplace=True),
            nn.MaxPool2d(kernel_size=3, stride=2),                  # output[256, 27, 27]

            nn.Conv2d(256, 512, kernel_size=3, padding=1),          # output[512, 27, 27]
            nn.ReLU(inplace=True),

            nn.Conv2d(512, 1024, kernel_size=3, padding=1),          # output[1024, 27, 27]
            nn.ReLU(inplace=True),

            nn.Conv2d(1024, 512, kernel_size=3, padding=1),          # output[512, 27, 27]
            nn.ReLU(inplace=True),
            nn.MaxPool2d(kernel_size=3, stride=2),                  # output[512, 13, 13]
        )
        self.classifier = nn.Sequential(
            nn.Dropout(p=0.5),
            nn.Linear(512 * 13 * 13, 4096),
            nn.ReLU(inplace=True),

            nn.Dropout(p=0.5),
            nn.Linear(4096, 4096),
            nn.ReLU(inplace=True),
            
            nn.Linear(4096, num_classes),
        )
        if init_weights:
            self._initialize_weights()

    def forward(self, x):
        x = self.features(x)
        x = torch.flatten(x, start_dim=1)
        x = self.classifier(x)
        return x

    def _initialize_weights(self):
        for m in self.modules():
            if isinstance(m, nn.Conv2d):
                nn.init.kaiming_normal_(m.weight, mode='fan_out', nonlinearity='relu')
                if m.bias is not None:
                    nn.init.constant_(m.bias, 0)
            elif isinstance(m, nn.Linear):
                nn.init.normal_(m.weight, 0, 0.01)
                nn.init.constant_(m.bias, 0)

def zfnet(num_classes): 
    model = ZFNet(num_classes=num_classes)
    return model

VGGNet：使用块的网络 (2014)

VGGNet概述

Paper : 《Very Deep Convolutional Networks for Large-Scale Image Recognition》
Code: pytorch/vision

VGGNet由牛津大学计算机视觉组合和Google DeepMind公司研究员一起研发的深度卷积神经网络。它探索了卷积神经网络的深度和其性能之间的关系，通过反复的堆叠33的小型卷积核和22的最大池化层，成功的构建了16~19层深的卷积神经网络。VGGNet获得了ILSVRC 2014年比赛的亚军和定位项目的冠军，在top5上的错误率为7.5%。目前为止，VGGNet依然被用来提取图像的特征。
VGGNet全部使用3*3的卷积核和2*2的池化核，通过不断加深网络结构来提升性能。网络层数的增长并不会带来参数量上的爆炸，因为参数量主要集中在最后三个全连接层中。同时，两个3*3卷积层的串联相当于1个5*5的卷积层，3个3*3的卷积层串联相当于1个7*7的卷积层，即3个3*3卷积层的感受野大小相当于1个7*7的卷积层。但是3个3*3的卷积层参数量只有7*7的一半左右，同时前者可以有3个非线性操作，而后者只有1个非线性操作，这样使得前者对于特征的学习能力更强。
VGGNet作者总结出LRN层作用不大，越深的网络效果越好，1*1的卷积也是很有效的，但是没有3*3的卷积效果好，因为3*3的网络可以学习到更大的空间特征。

VGGNet的网络结构
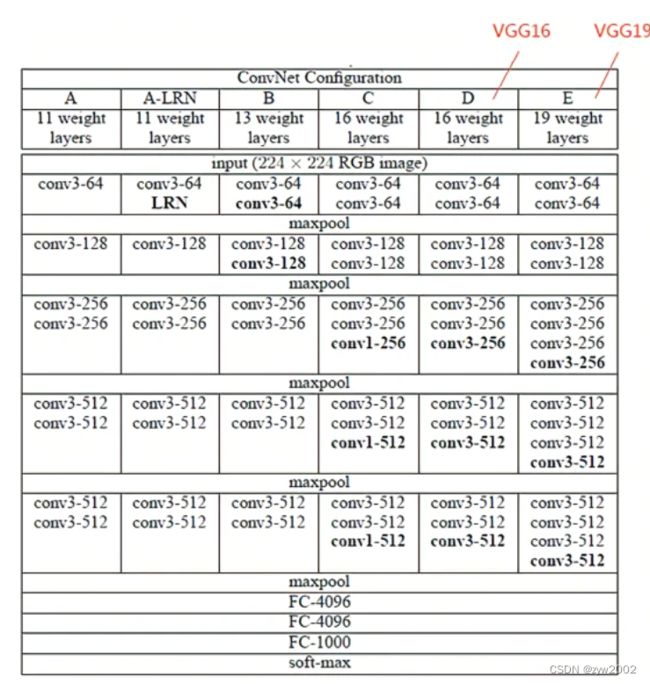
经典卷积神经网络详解（AlexNet、VGG、NiN、GoogLeNet、ResNet、DenseNet、CSPNet、Darknet、EfficientNet、SqueezeNet..）_第18张图片
VGGNet一共有六种不同的网络结构A(VGG11)、A-LRN（VGG11-LRN）、B(VGG13)、C(VGG16-1)、D(VGG16-3)、E(VGG-19)，这6种网络结构相似，都是由5层卷积层、3层全连接层组成，其中区别在于每个卷积层的子层数量不同，从A至E依次增加（子层数量从1到4），总的网络深度从11层到19层（添加的层以粗体显示）。
VGG11-LRN表示在第一层中采用了LRN的VGG-11;VGG16-1表示后三组卷积块中最后一层卷积采用卷积核尺寸为1x1, 相应的VGG16-3表示卷积核尺寸为3x3。
表格中的卷积层参数表示为“conv⟨感受野大小⟩-通道数⟩”，例如con3-128，表示使用3x3的卷积核，通道数为128。为了简洁起见，在表格中不显示ReLU激活功能。

以VGG-16为例，架构图如下：
经典卷积神经网络详解（AlexNet、VGG、NiN、GoogLeNet、ResNet、DenseNet、CSPNet、Darknet、EfficientNet、SqueezeNet..）_第19张图片
VGG-16架构：13个卷积层+3个全连接层，前5段卷积网络（标号1-5），最后一段全连接网络（标号6-8），网络总共参数数量大约138M左右。。

(1) 输入层(Input)：图像大小为224×224×3

(2) 卷积层1+ReLU：conv3 - 64（卷积核的数量）：kernel size:3 stride:1 pad:1
像素：（224-3+2×1）/1+1=224 输出为224×224×64 64个feature maps
参数： （3×3×3）×64+64=1792

(3) 卷积层2+ReLU：conv3 - 64：kernel size:3 stride:1 pad:1
像素： （224-3+1×2）/1+1=224 输出为224×224×64 64个feature maps
参数： (3×3×64×64)+64=36928

(4) 最大池化层： pool2： kernel size:2 stride:2 pad:0
像素： （224-2）/2 = 112 输出为112×112×64，64个feature maps
参数： 0

(5) 卷积层3+ReLU：.conv3-128:kernel size:3 stride:1 pad:1
像素： （112-3+2×1）/1+1 = 112 输出为112×112×128，128个feature maps
参数： (3×3×64×128)+128=73856

(6) 卷积层4+ReLU：conv3-128:kernel size:3 stride:1 pad:1
像素： （112-3+2×1）/1+1 = 112 输出为112×112×128，128个feature maps
参数： (3×3×128×128)+128=147584

(7) 最大池化层：pool2: kernel size:2 stride:2 pad:0
像素： （112-2）/2+1=56 输出为56×56×128，128个feature maps。
参数： 0

(8) 卷积层5+ReLU：conv3-256: kernel size:3 stride:1 pad:1
像素： （56-3+2×1）/1+1=56 输出为56×56×256，256个feature maps
参数： (3×3×128×256)+256=295168

(9) 卷积层6+ReLU：conv3-256: kernel size:3 stride:1 pad:1
像素： （56-3+2×1）/1+1=56 输出为56×56×256，256个feature maps，
参数： (3×3×256×256)+256=590080

(10) 卷积层7+ReLU：conv3-256: kernel size:3 stride:1 pad:1
像素： （56-3+2×1）/1+1=56 输出为56×56×256，256个feature maps
参数： (3×3×256×256)+256=590080

(11) 最大池化层：pool2: kernel size:2 stride:2 pad:0
像素：（56 - 2）/2+1=28 输出为28×28×256，256个feature maps
参数： 0

(12) 卷积层8+ReLU：conv3-512:kernel size:3 stride:1 pad:1
像素：（28-3+2×1）/1+1=28 输出为28×28×512，512个feature maps
参数： (3×3×256×512)+512=1180160

(13) 卷积层9+ReLU：conv3-512:kernel size:3 stride:1 pad:1
像素：（28-3+2×1）/1+1=28 输出为28×28×512，512个feature maps
参数： (3×3×512×512)+512=2359808

(14) 卷积层10+ReLU：conv3-512:kernel size:3 stride:1 pad:1
像素：（28-3+2×1）/1+1=28 输出为28×28×512，512个feature maps
参数： (3×3×512×512)+512=2359808

(15) 最大池化层：pool2: kernel size:2 stride:2 pad:0，输出为14×14×512，512个feature maps。
像素：（28-2）/2+1=14 输出为14×14×512
参数： 0

(16) 卷积层11+ReLU：conv3-512:kernel size:3 stride:1 pad:1
像素：（14-3+2×1）/1+1=14 输出为14×14×512，512个feature maps
参数： (3×3×512×512)+512=2359808

(17) 卷积层12+ReLU：conv3-512:kernel size:3 stride:1 pad:1
像素：（14-3+2×1）/1+1=14 输出为14×14×512，512个feature maps
参数： (3×3×512×512)+512=2359808

(18) 卷积层13+ReLU：conv3-512:kernel size:3 stride:1 pad:1
像素：（14-3+2×1）/1+1=14 输出为14×14×512，512个feature maps，
参数： (3×3×512×512)+512=2359808

(19) 最大池化层：pool2:kernel size:2 stride:2 pad:0
像素：（14-2）/2+1=7 输出为7×7×512，512个feature maps
参数： 0

(20) 全连接层1+ReLU+Dropout：有4096个神经元或4096个feature maps
像素：1×1×4096
参数：7×7×512×4096 = 102760448

(21) 全连接层2+ReLU+Dropout：有4096个神经元或4096个feature maps
像素：1×1×4096
参数：4096×4096 = 16777216

(22) 全连接层3：有1000个神经元或1000个feature maps
像素：1×1×1000
参数：4096×1000=4096000

(23) 输出层(Softmax)：输出识别结果，看它究竟是1000个可能类别中的哪一个。

VGGNet的代码实现
经典卷积神经网络的基本组成部分是下面的这个序列：

  1. 带填充以保持分辨率的卷积层；
  2. 非线性激活函数，如ReLU；
  3. 汇聚层，如最大汇聚层。
    作者使用了带有3×3卷积核、填充为1（保持高度和宽度）的卷积层，和带有2×2汇聚窗口、步幅为2（每个块后的分辨率减半）的最大汇聚层。在下面的代码中，我们定义了一个名为vgg_block的函数来实现一个VGG块。

该函数有三个参数，分别对应于卷积层的数量num_convs、输入通道的数量in_channels和输出通道的数量out_channels

import torch
from torch import nn
from d2l import torch as d2l

def vgg_block(num_convs, in_channels, out_channels):
    layers = []
    for _ in range(num_convs):
        layers.append(nn.Conv2d(in_channels, out_channels,
                                kernel_size=3, padding=1))
        layers.append(nn.ReLU())
        in_channels = out_channels
    layers.append(nn.MaxPool2d(kernel_size=2,stride=2))
    return nn.Sequential(*layers)

VGG网络可以分为两部分：第一部分主要由卷积层和汇聚层组成，第二部分由全连接层组成。
在这里插入图片描述

VGG神经网络连接几个VGG块（在vgg_block函数中定义）。其中有超参数变量conv_arch。该变量指定了每个VGG块里卷积层个数和输出通道数。全连接模块则与AlexNet中的相同。

原始VGG网络有5个卷积块，其中前两个块各有一个卷积层，后三个块各包含两个卷积层。 第一个模块有64个输出通道，每个后续模块将输出通道数量翻倍，直到该数字达到512。由于该网络使用8个卷积层和3个全连接层，因此它通常被称为VGG-11。

conv_arch = ((1, 64), (1, 128), (2, 256), (2, 512), (2, 512))

下面的代码实现了VGG-11。可以通过在conv_arch上执行for循环来简单实现。

def vgg(conv_arch):
    conv_blks = []
    in_channels = 1
    # 卷积层部分
    for (num_convs, out_channels) in conv_arch:
        conv_blks.append(vgg_block(num_convs, in_channels, out_channels))
        in_channels = out_channels

    return nn.Sequential(
        *conv_blks, nn.Flatten(),
        # 全连接层部分
        nn.Linear(out_channels * 7 * 7, 4096), nn.ReLU(), nn.Dropout(0.5),
        nn.Linear(4096, 4096), nn.ReLU(), nn.Dropout(0.5),
        nn.Linear(4096, 10))

net = vgg(conv_arch)

接下来，我们将构建一个高度和宽度为224的单通道数据样本，以观察每个层输出的形状。

X = torch.randn(size=(1, 1, 224, 224))
for blk in net:
    X = blk(X)
    print(blk.__class__.__name__,'output shape:\t',X.shape)

Sequential output shape:     torch.Size([1, 64, 112, 112])
Sequential output shape:     torch.Size([1, 128, 56, 56])
Sequential output shape:     torch.Size([1, 256, 28, 28])
Sequential output shape:     torch.Size([1, 512, 14, 14])
Sequential output shape:     torch.Size([1, 512, 7, 7])
Flatten output shape:        torch.Size([1, 25088])
Linear output shape:         torch.Size([1, 4096])
ReLU output shape:   torch.Size([1, 4096])
Dropout output shape:        torch.Size([1, 4096])
Linear output shape:         torch.Size([1, 4096])
ReLU output shape:   torch.Size([1, 4096])
Dropout output shape:        torch.Size([1, 4096])
Linear output shape:         torch.Size([1, 10])

正如你所看到的，我们在每个块的高度和宽度减半，最终高度和宽度都为7。最后再展平表示，送入全连接层处理。

  • 训练模型

由于VGG-11比AlexNet计算量更大，因此我们构建了一个通道数较少的网络，足够用于训练Fashion-MNIST数据集。

ratio = 4
small_conv_arch = [(pair[0], pair[1] // ratio) for pair in conv_arch]
net = vgg(small_conv_arch)

除了使用略高的学习率外，模型训练过程与 AlexNet类似。

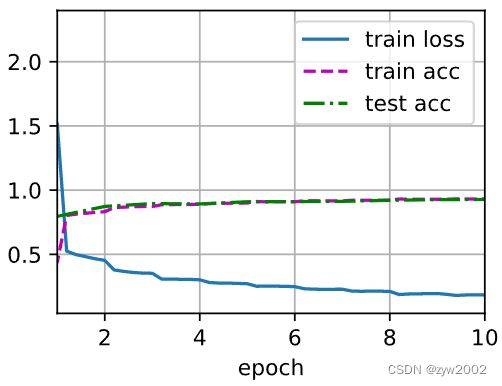
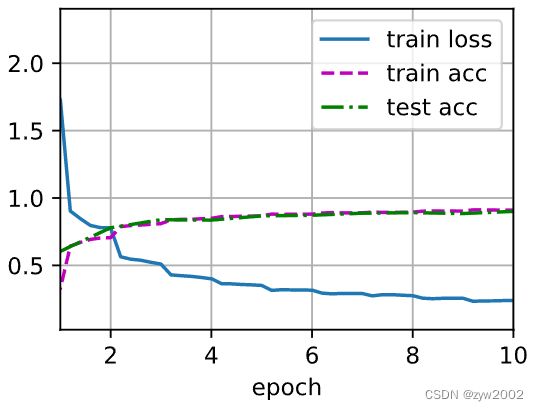
lr, num_epochs, batch_size = 0.05, 10, 128
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size, resize=224)
d2l.train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())

loss 0.177, train acc 0.934, test acc 0.911
2562.3 examples/sec on cuda:0

经典卷积神经网络详解（AlexNet、VGG、NiN、GoogLeNet、ResNet、DenseNet、CSPNet、Darknet、EfficientNet、SqueezeNet..）_第20张图片

VGGNet 小结：

VGG网络的特点是利用小的尺寸核代替大的卷积核，然后把网络做深。

  • 结构简洁 : 卷积层+ReLU、最大池化层、全连接层、Softmax输出层。
    VGGNet的结构十分简洁，由5个卷积层、3个全连接层和1个softmax层构成，层与层之间使用最大池化连接，隐藏层之间使用的激活函数全都是ReLU。
  • 使用小卷积核
    使用多个3×3卷积堆叠的作用有两个：一是在不影响感受野的前提下减少了参数；二是增加了网络的非线性,从而提升网络的表达能力。
  • 使用小滤波器
    与AlexNet相比，VGGNet在池化层全部采用的是2×2的小滤波器，stride为2。
  • 通道数较多
    VGGNet的第一层有64个通道，后面的每一层都对通道进行了翻倍，最多达到了512个通道（ 64-128-256-512-512）。由于每个通道都代表着一个feature map，这样就使更多的信息可以被提取出来。
  • 图像预处理
    训练采用多尺度训练（Multi-scale），将原始图像缩放到不同尺寸 S，然后再随机裁切224x224的图片，并且对图片进行水平翻转和随机RGB色差调整，这样能增加很多数据量，对于防止模型过拟合有很不错的效果。
  • 将全连接层转换为卷积层
    这个特征是体现在VGGNet的测试阶段。在进行网络测试时，将训练阶段的3个全连接层替换为3个卷积层，使测试得到的网络没有全连接的限制，能够接收任意宽和高的输入。如果后面3个层都是全连接层，那么在测试阶段就只能将测试的图像全部缩放到固定尺寸，这样就不便于多尺度测试工作的开展。
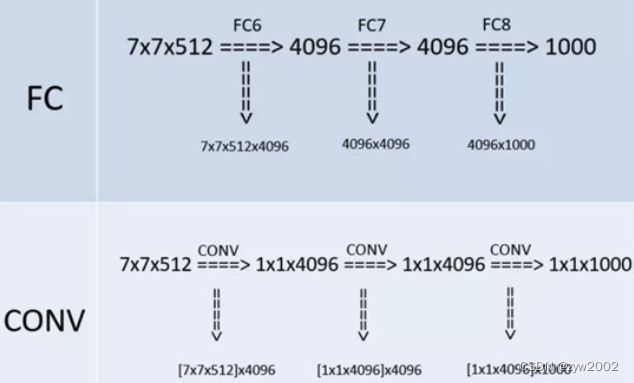
    经典卷积神经网络详解（AlexNet、VGG、NiN、GoogLeNet、ResNet、DenseNet、CSPNet、Darknet、EfficientNet、SqueezeNet..）_第21张图片
    1*1的卷积层常被用来提炼特征，即多通道的特征组合在一起，凝练成较大通道或者较小通道的输出，而每张图片的大小不变。有时1*1的卷积神经网络还可以用来替代全连接层。

NiN： 网络中的网络 （2014）

NiN的概述

Paper : 《Network In Network》
Code: pytorch/vision

Network In NetWork(NIN) 是由新加坡国立大学的MinLin 等人提出的，在CIFAR-10和CIFAR-100分类任务中达到了SOTA结果。提出mlpconv，引入了1x1卷积和global average pooling，提出Network In Network(NIN)，整个模型未使用全连接。模型不够深，迁移能力有待加强。

LeNet、AlexNet和VGG都有一个共同的设计模式：通过一系列的卷积层与汇聚层来提取空间结构特征；然后通过全连接层对特征的表征进行处理。 AlexNet和VGG对LeNet的改进主要在于如何扩大和加深这两个模块。
AlexNet和VGG都是先由卷积层构成的模块充分抽取空间特征，再由全连接层构成的模块来输出分类结果。然而，如果使用了全连接层，可能会完全放弃表征的空间结构，且参数量巨大。 因此NiN提出用1*1卷积代替全连接层，串联多个由卷积层和“全连接”层构成的小网络来构建⼀个深层网络。

NiN的网络结构

NIN由三层感知卷积层（MLPConv Layer） 构成。
每一层MLPConv Layer内部由若干个局部的全连接层和非线性激活函数组成，代替了传统卷积层中采用的线性卷积核。
线性卷积层和mlpconv都是将局部感受野(local receptive field)映射到输出特征向量。Mlpconv核使用带非线性激活函数的MLP，跟传统的CNN一样，MLP在各个局部感受野中共享参数的，滑动MLP核可以最终得到输出特征图。
优点是：1. 提供了网络层间映射的一种新可能；2. 增加了网络卷积层的非线性能力。
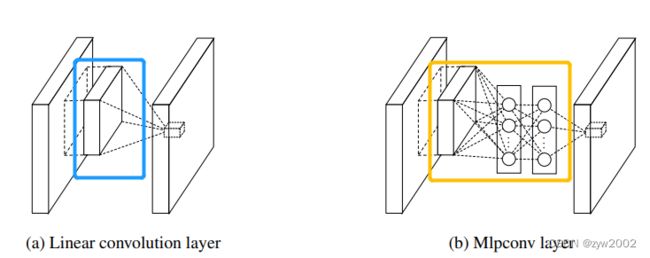
经典卷积神经网络详解（AlexNet、VGG、NiN、GoogLeNet、ResNet、DenseNet、CSPNet、Darknet、EfficientNet、SqueezeNet..）_第22张图片
传统的CNN模型先是使用堆叠的卷积层提取特征，输入全连接层(FC)进行分类。这种结构沿袭自LeNet5，把卷积层作为特征抽取器，全连接层作为分类器。但是FC层参数数量太多，很容易过拟合，会影响模型的泛化性能。因此需要用Dropout增加模型的泛化性。
在NIN中，卷积层后不接全连接层(FC)，而是将最后一个的mlpconv的输出每个特征图全局平均池化(global average pooling，GAP) ，而后softmax。

经典卷积神经网络详解（AlexNet、VGG、NiN、GoogLeNet、ResNet、DenseNet、CSPNet、Darknet、EfficientNet、SqueezeNet..）_第23张图片
GAP的优点：

  1. 加强了特征映射和类别之间的对应，更适合卷积神经网络，特征图可以被解释类别置信度。
  2. GAP层不用优化参数，可以避免过拟合。
    GAP对空间信息进行汇总，因此对输入数据的空间变换有更好的鲁棒性。
  3. 可以将GAP看做一个结构正则化器，显性地强制特征图映射为概念置信度。

NiN的代码实现

  • NiN块

卷积层的输入和输出由四维张量组成，张量的每个轴分别对应样本、通道、高度和宽度。 另外，全连接层的输入和输出通常是分别对应于样本和特征的二维张量。 NiN的想法是在每个像素位置（针对每个高度和宽度）应用一个全连接层。 如果我们将权重连接到每个空间位置，我们可以将其视为1×1卷积层，或作为在每个像素位置上独立作用的全连接层。 从另一个角度看，即将空间维度中的每个像素视为单个样本，将通道维度视为不同特征（feature）。

下图说明了VGG和NiN及它们的块之间主要架构差异。 NiN块以一个普通卷积层开始，后面是两个1×1的卷积层。这两个1×1卷积层充当带有ReLU激活函数的逐像素全连接层。 第一层的卷积窗口形状通常由用户设置。 随后的卷积窗口形状固定为1×1。

经典卷积神经网络详解（AlexNet、VGG、NiN、GoogLeNet、ResNet、DenseNet、CSPNet、Darknet、EfficientNet、SqueezeNet..）_第24张图片

import torch
from torch import nn
from d2l import torch as d2l

def nin_block(in_channels, out_channels, kernel_size, strides, padding):
    return nn.Sequential(
        nn.Conv2d(in_channels, out_channels, kernel_size, strides, padding),
        nn.ReLU(),
        nn.Conv2d(out_channels, out_channels, kernel_size=1), nn.ReLU(),
        nn.Conv2d(out_channels, out_channels, kernel_size=1), nn.ReLU())
  • NiN模型

最初的NiN网络是在AlexNet后不久提出的，显然从中得到了一些启示。 NiN使用窗口形状为11×11、5×5和3×3的卷积层，输出通道数量与AlexNet中的相同。 每个NiN块后有一个最大汇聚层，汇聚窗口形状为3×3，步幅为2。

NiN和AlexNet之间的一个显著区别是NiN完全取消了全连接层。 相反，NiN使用一个NiN块，其输出通道数等于标签类别的数量。最后放一个全局平均汇聚层（global average pooling layer），生成一个对数几率 （logits）。NiN设计的一个优点是，它显著减少了模型所需参数的数量。然而，在实践中，这种设计有时会增加训练模型的时间。

net = nn.Sequential(
    nin_block(1, 96, kernel_size=11, strides=4, padding=0),
    nn.MaxPool2d(3, stride=2),
    nin_block(96, 256, kernel_size=5, strides=1, padding=2),
    nn.MaxPool2d(3, stride=2),
    nin_block(256, 384, kernel_size=3, strides=1, padding=1),
    nn.MaxPool2d(3, stride=2),
    nn.Dropout(0.5),
    # 标签类别数是10
    nin_block(384, 10, kernel_size=3, strides=1, padding=1),
    nn.AdaptiveAvgPool2d((1, 1)),
    # 将四维的输出转成二维的输出，其形状为(批量大小,10)
    nn.Flatten())

我们创建一个数据样本来查看每个块的输出形状。

X = torch.rand(size=(1, 1, 224, 224))
for layer in net:
    X = layer(X)
    print(layer.__class__.__name__,'output shape:\t', X.shape)

Sequential output shape:     torch.Size([1, 96, 54, 54])
MaxPool2d output shape:      torch.Size([1, 96, 26, 26])
Sequential output shape:     torch.Size([1, 256, 26, 26])
MaxPool2d output shape:      torch.Size([1, 256, 12, 12])
Sequential output shape:     torch.Size([1, 384, 12, 12])
MaxPool2d output shape:      torch.Size([1, 384, 5, 5])
Dropout output shape:        torch.Size([1, 384, 5, 5])
Sequential output shape:     torch.Size([1, 10, 5, 5])
AdaptiveAvgPool2d output shape:      torch.Size([1, 10, 1, 1])
Flatten output shape:        torch.Size([1, 10])
  • 训练模型
lr, num_epochs, batch_size = 0.1, 10, 128
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size, resize=224)
d2l.train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())

loss 0.363, train acc 0.865, test acc 0.879
3212.2 examples/sec on cuda:0

经典卷积神经网络详解（AlexNet、VGG、NiN、GoogLeNet、ResNet、DenseNet、CSPNet、Darknet、EfficientNet、SqueezeNet..）_第25张图片

NiN小结

  • NiN使用由一个卷积层和多个1×1卷积层组成的块。该块可以在卷积神经网络中使用，以允许更多的每像素非线性。
  • NiN去除了容易造成过拟合的全连接层，将它们替换为全局平均汇聚层（即在所有位置上进行求和）。该汇聚层通道数量为所需的输出数量（例如，Fashion-MNIST的输出为10）。
  • 移除全连接层可减少过拟合，同时显著减少NiN的参数。
  • NiN的设计影响了许多后续卷积神经网络的设计,如ResNet, Inception，GoogLeNet等网络。

GoogLeNet : 含并行连接的网络 (2014)

GoogLeNet的概述

Paper : 《Going Deeper with Convolutions》
Code: pytorch/vision

GoogleNet 网络是14年由 Google 团队提出，斩获该年 ImageNet 竞赛中 Classification Task（分类任务）第一名。之所以名为“GoogLeNet”而非“GoogleNet”,文章说是为了向早期的LeNet致敬。

GoogLeNet吸收了NiN中串联网络的思想，并在此基础上做了改进。 这篇论文的一个重点是解决了什么样大小的卷积核最合适的问题。 毕竟，以前流行的网络使用小到1×1，大到11×11的卷积核。 本文的一个观点是，有时使用不同大小的卷积核组合是有利的。
大量的文献表明可以将稀疏矩阵聚类为较为密集的子矩阵来提高计算性能，据此论文提出了名为Inception 的结构来实现此目的，既能保持网络结构的稀疏性，又能利用密集矩阵的高计算性能。

GoogLeNet的网络结构

  • Inception结构
    Inception 结构的主要思路是怎样用密集成分来近似最优的局部稀疏结构。
    作者首先提出下图这样的基本结构：
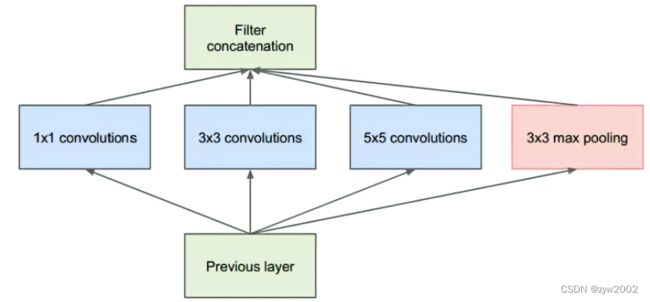
    经典卷积神经网络详解（AlexNet、VGG、NiN、GoogLeNet、ResNet、DenseNet、CSPNet、Darknet、EfficientNet、SqueezeNet..）_第26张图片
    对上图做以下说明：
    1 . 采用不同大小的卷积核意味着不同大小的感受野，最后拼接意味着不同尺度特征的融合；
    2 . 之所以卷积核大小采用1、3和5，主要是为了方便对齐。设定卷积步长stride=1之后，只要分别设定pad=0、1、2，那么卷积之后便可以得到相同维度的特征，然后这些特征就可以直接拼接在一起了；
    3 . 文章说很多地方都表明pooling挺有效，所以Inception里面也嵌入了。
    4 . 网络越到后面，特征越抽象，而且每个特征所涉及的感受野也更大了，因此随着层数的增加，3x3和5x5卷积的比例也要增加。

但是，使用5x5的卷积核仍然会带来巨大的计算量。 为此，文章借鉴NIN2，采用1x1卷积核来进行降维。
例如：上一层的输出为100x100x128，经过具有256个输出的5x5卷积层之后(stride=1，pad=2)，输出数据为100x100x256。其中，卷积层的参数为128x5x5x256。假如上一层输出先经过具有32个输出的1x1卷积层，再经过具有256个输出的5x5卷积层，那么最终的输出数据仍为为100x100x256，但卷积参数量已经减少为128x1x1x32 + 32x5x5x256，大约减少了4倍。
具体改进后的Inception Module如下图：
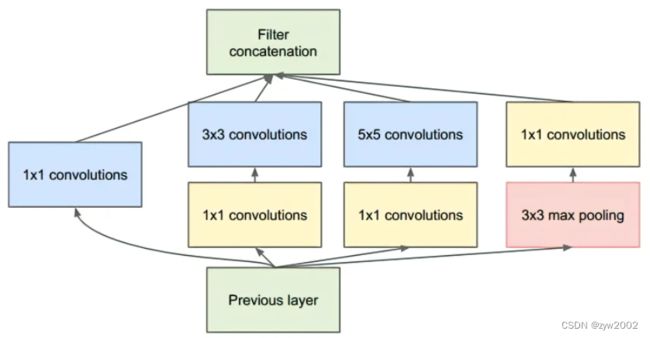
经典卷积神经网络详解（AlexNet、VGG、NiN、GoogLeNet、ResNet、DenseNet、CSPNet、Darknet、EfficientNet、SqueezeNet..）_第27张图片
Inception块由四条并行路径组成。 前三条路径使用窗口大小为1×1、3×3和5×5的卷积层，从不同空间大小中提取信息。 中间的两条路径在输入上执行1×1卷积，以减少通道数，从而降低模型的复杂性。 第四条路径使用3×3最大汇聚层，然后使用1×1卷积层来改变通道数。 这四条路径都使用合适的填充来使输入与输出的高和宽一致，最后我们将每条线路的输出在通道维度上连结，并构成Inception块的输出。在Inception块中，通常调整的超参数是每层输出通道数。
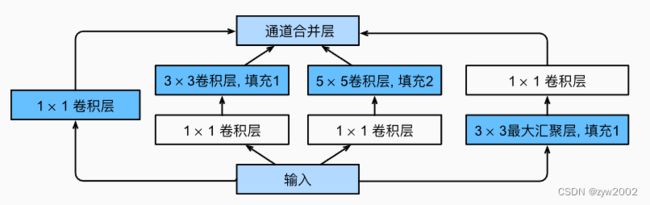
经典卷积神经网络详解（AlexNet、VGG、NiN、GoogLeNet、ResNet、DenseNet、CSPNet、Darknet、EfficientNet、SqueezeNet..）_第28张图片

GoogLeNet一共使用9个Inception块和全局平均汇聚层的堆叠来生成其估计值。Inception块之间的最大汇聚层可降低维度。 第一个模块类似于AlexNet和LeNet，Inception块的组合从VGG继承，全局平均汇聚层避免了在最后使用全连接层。
经典卷积神经网络详解（AlexNet、VGG、NiN、GoogLeNet、ResNet、DenseNet、CSPNet、Darknet、EfficientNet、SqueezeNet..）_第29张图片

GoogLeNet的代码实现

  • Inception 块
import torch
from torch import nn
from torch.nn import functional as F
from d2l import torch as d2l

class Inception(nn.Module):
    # c1--c4是每条路径的输出通道数
    def __init__(self, in_channels, c1, c2, c3, c4, **kwargs):
        super(Inception, self).__init__(**kwargs)
        # 线路1，单1x1卷积层
        self.p1_1 = nn.Conv2d(in_channels, c1, kernel_size=1)
        # 线路2，1x1卷积层后接3x3卷积层
        self.p2_1 = nn.Conv2d(in_channels, c2[0], kernel_size=1)
        self.p2_2 = nn.Conv2d(c2[0], c2[1], kernel_size=3, padding=1)
        # 线路3，1x1卷积层后接5x5卷积层
        self.p3_1 = nn.Conv2d(in_channels, c3[0], kernel_size=1)
        self.p3_2 = nn.Conv2d(c3[0], c3[1], kernel_size=5, padding=2)
        # 线路4，3x3最大汇聚层后接1x1卷积层
        self.p4_1 = nn.MaxPool2d(kernel_size=3, stride=1, padding=1)
        self.p4_2 = nn.Conv2d(in_channels, c4, kernel_size=1)

    def forward(self, x):
        p1 = F.relu(self.p1_1(x))
        p2 = F.relu(self.p2_2(F.relu(self.p2_1(x))))
        p3 = F.relu(self.p3_2(F.relu(self.p3_1(x))))
        p4 = F.relu(self.p4_2(self.p4_1(x)))
        # 在通道维度上连结输出
        return torch.cat((p1, p2, p3, p4), dim=1)
  • GoogLeNet模型
    现在，我们逐一实现GoogLeNet的每个模块。第一个模块使用64个通道、7×7卷积层。
b1 = nn.Sequential(nn.Conv2d(1, 64, kernel_size=7, stride=2, padding=3),
                   nn.ReLU(),
                   nn.MaxPool2d(kernel_size=3, stride=2, padding=1))

第二个模块使用两个卷积层：第一个卷积层是64个通道、1×1卷积层；第二个卷积层使用将通道数量增加三倍的3×3卷积层。 这对应于Inception块中的第二条路径。

b2 = nn.Sequential(nn.Conv2d(64, 64, kernel_size=1),
                   nn.ReLU(),
                   nn.Conv2d(64, 192, kernel_size=3, padding=1),
                   nn.ReLU(),
                   nn.MaxPool2d(kernel_size=3, stride=2, padding=1))

第三个模块串联两个完整的Inception块。 第一个Inception块的输出通道数为64+128+32+32=256，四个路径之间的输出通道数量比为64:128:32:32=2:4:1:1
。 第二个和第三个路径首先将输入通道的数量分别减少到96/192=1/2
和16/192=1/12，然后连接第二个卷积层。第二个Inception块的输出通道数增加到128+192+96+64=480，四个路径之间的输出通道数量比为128:192:96:64=4:6:3:2。 第二条和第三条路径首先将输入通道的数量分别减少到128/256=1/2和32/256=1/8。

b3 = nn.Sequential(Inception(192, 64, (96, 128), (16, 32), 32),
                   Inception(256, 128, (128, 192), (32, 96), 64),
                   nn.MaxPool2d(kernel_size=3, stride=2, padding=1))

第四模块更加复杂， 它串联了5个Inception块，其输出通道数分别是192+208+48+64=512、160+224+64+64=512、128+256+64+64=512、112+288+64+64=528和256+320+128+128=832。 这些路径的通道数分配和第三模块中的类似，首先是含3×3卷积层的第二条路径输出最多通道，其次是仅含1×1卷积层的第一条路径，之后是含5×5卷积层的第三条路径和含3×3最大汇聚层的第四条路径。 其中第二、第三条路径都会先按比例减小通道数。 这些比例在各个Inception块中都略有不同。

b4 = nn.Sequential(Inception(480, 192, (96, 208), (16, 48), 64),
                   Inception(512, 160, (112, 224), (24, 64), 64),
                   Inception(512, 128, (128, 256), (24, 64), 64),
                   Inception(512, 112, (144, 288), (32, 64), 64),
                   Inception(528, 256, (160, 320), (32, 128), 128),
                   nn.MaxPool2d(kernel_size=3, stride=2, padding=1))

第五模块包含输出通道数为256+320+128+128=832和384+384+128+128=1024的两个Inception块。 其中每条路径通道数的分配思路和第三、第四模块中的一致，只是在具体数值上有所不同。 需要注意的是，第五模块的后面紧跟输出层，该模块同NiN一样使用全局平均汇聚层，将每个通道的高和宽变成1。 最后我们将输出变成二维数组，再接上一个输出个数为标签类别数的全连接层。

b5 = nn.Sequential(Inception(832, 256, (160, 320), (32, 128), 128),
                   Inception(832, 384, (192, 384), (48, 128), 128),
                   nn.AdaptiveAvgPool2d((1,1)),
                   nn.Flatten())

net = nn.Sequential(b1, b2, b3, b4, b5, nn.Linear(1024, 10))

GoogLeNet模型的计算复杂，而且不如VGG那样便于修改通道数。 为了使Fashion-MNIST上的训练短小精悍，我们将输入的高和宽从224降到96，这简化了计算。下面演示各个模块输出的形状变化。

X = torch.rand(size=(1, 1, 96, 96))
for layer in net:
    X = layer(X)
    print(layer.__class__.__name__,'output shape:\t', X.shape)

Sequential output shape:     torch.Size([1, 64, 24, 24])
Sequential output shape:     torch.Size([1, 192, 12, 12])
Sequential output shape:     torch.Size([1, 480, 6, 6])
Sequential output shape:     torch.Size([1, 832, 3, 3])
Sequential output shape:     torch.Size([1, 1024])
Linear output shape:         torch.Size([1, 10])
  • 训练模型

和以前一样，我们使用Fashion-MNIST数据集来训练我们的模型。在训练之前，我们将图片转换为96×96分辨率。

lr, num_epochs, batch_size = 0.1, 10, 128
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size, resize=96)
d2l.train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())

loss 0.254, train acc 0.904, test acc 0.885
3570.5 examples/sec on cuda:0

经典卷积神经网络详解（AlexNet、VGG、NiN、GoogLeNet、ResNet、DenseNet、CSPNet、Darknet、EfficientNet、SqueezeNet..）_第30张图片

GoogLeNet 小结

  • Inception块相当于一个有4条路径的子网络。它通过不同窗口形状的卷积层和最大汇聚层来并行抽取信息，并使用1×1卷积层减少每像素级别上的通道维数从而降低模型复杂度。
  • GoogLeNet将多个设计精细的Inception块与其他层（卷积层、全连接层）串联起来。其中Inception块的通道数分配之比是在ImageNet数据集上通过大量的实验得来的。
  • GoogLeNet和它的后继者们一度是ImageNet上最有效的模型之一：它以较低的计算复杂度提供了类似的测试精度。

ResNet: 残差网络 （2015）

ResNet的概述

Paper : Deep Residual Learning for Image Recognition
Code: pytorch/vision/models/resnet.py

ResNet 网络是在 2015年 由微软实验室中的何凯明等几位大神提出，斩获当年ImageNet竞赛中分类任务第一名，目标检测第一名。获得COCO数据集中目标检测第一名，图像分割第一名。

ResNet的主要贡献：

  1. 超深的网络结构（超过1000层）。
  2. 提出residual（残差结构）模块。
  3. 使用Batch Normalization 加速训练（丢弃dropout）。

ResNet的提出背景：
在ResNet提出之前，所有的神经网络都是通过卷积层和池化层的叠加组成的。
人们认为卷积层和池化层的层数越多，获取到的图片特征信息越全，学习效果也就越好。但是在实际的试验中发现，随着卷积层和池化层的叠加，不但没有出现学习效果越来越好的情况，反而两种问题：

  1. 梯度消失和梯度爆炸
    梯度消失：若每一层的误差梯度小于1，反向传播时，网络越深，梯度越趋近于0
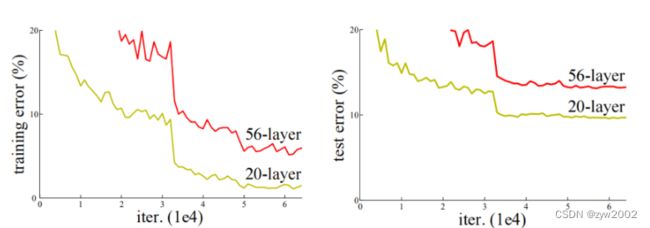
    梯度爆炸：若每一层的误差梯度大于1，反向传播时，网络越深，梯度越来越大
  2. 退化问题
    随着层数的增加，预测效果反而越来越差。如下图所示
    经典卷积神经网络详解（AlexNet、VGG、NiN、GoogLeNet、ResNet、DenseNet、CSPNet、Darknet、EfficientNet、SqueezeNet..）_第31张图片
  • 为了解决梯度消失或梯度爆炸问题，ResNet论文提出通过数据的预处理以及在网络中使用 BN（Batch Normalization）层来解决。
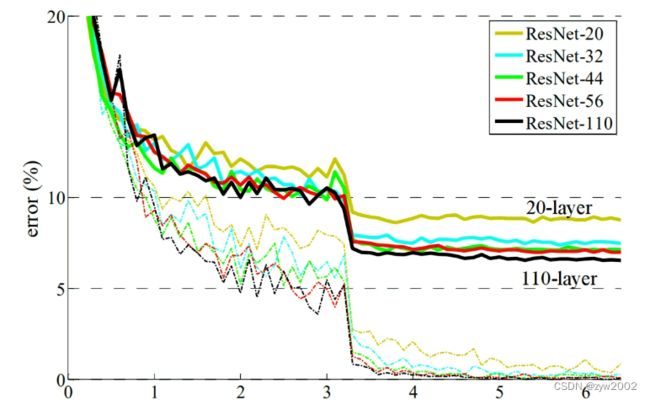
    Batch Normalization是指批标准化处理，将一批数据的feature map满足均值为0，方差为1的分布规律。
  • 为了解决深层网络中的退化问题，可以人为地让神经网络某些层跳过下一层神经元的连接，隔层相连，弱化每层之间的强联系。这种神经网络被称为 残差网络 (ResNets)。ResNet论文提出了 residual结构（残差结构）来减轻退化问题，下图是使用residual结构的卷积网络，可以看到随着网络的不断加深，效果并没有变差，而是变的更好了。（虚线是train error，实线是test error）
    经典卷积神经网络详解（AlexNet、VGG、NiN、GoogLeNet、ResNet、DenseNet、CSPNet、Darknet、EfficientNet、SqueezeNet..）_第32张图片

ResNet 的结构

  • Residual 的计算方式
    residual结构使用了一种shortcut的连接方式，也可理解为捷径。让特征矩阵隔层相加，注意F(X)和X形状要相同，所谓相加是特征矩阵相同位置上的数字进行相加。
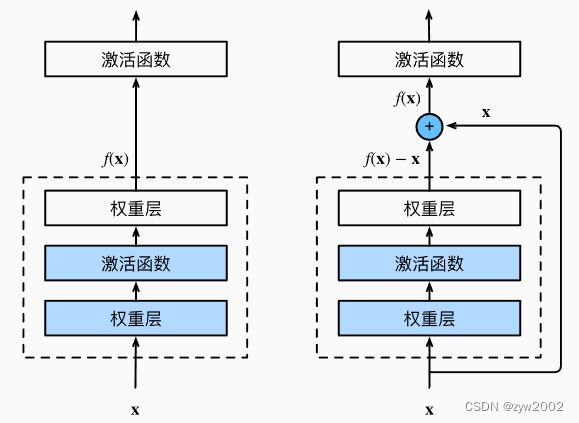
    经典卷积神经网络详解（AlexNet、VGG、NiN、GoogLeNet、ResNet、DenseNet、CSPNet、Darknet、EfficientNet、SqueezeNet..）_第33张图片
    如上，左图是一个正常的块，右图是一个残差块。
    让我们聚焦于神经网络局部：如图所示，假设我们的原始输入为x，而希望学出的理想映射为f(x)（作为上方激活函数的输入）。 左图虚线框中的部分需要直接拟合出该映射f(x)，而右图虚线框中的部分则需要拟合出残差映射f(x)−x。 残差映射在现实中往往更容易优化。 以本节开头提到的恒等映射作为我们希望学出的理想映射f(x)，我们只需将右图虚线框内上方的加权运算（如仿射）的权重和偏置参数设成0，那么f(x)即为恒等映射。 实际中，当理想映射f(x)极接近于恒等映射时，残差映射也易于捕捉恒等映射的细微波动。 右图是ResNet的基础架构–残差块（residual block）。 在残差块中，输入可通过跨层数据线路更快地向前传播。

  • 残差块
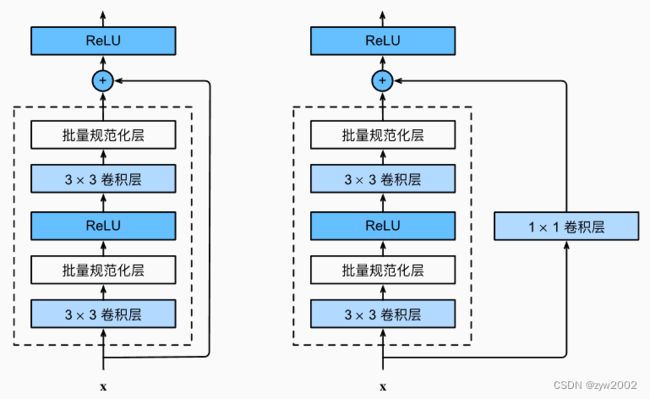    经典卷积神经网络详解（AlexNet、VGG、NiN、GoogLeNet、ResNet、DenseNet、CSPNet、Darknet、EfficientNet、SqueezeNet..）_第34张图片ResNet沿用了VGG完整的3×3卷积层设计。 残差块里首先有2个有相同输出通道数的3×3卷积层。 每个卷积层后接一个批量规范化层和ReLU激活函数。 然后我们通过跨层数据通路，跳过这2个卷积运算，将输入直接加在最后的ReLU激活函数前。 这样的设计要求2个卷积层的输出与输入形状一样，从而使它们可以相加。 如果想改变通道数，就需要引入一个额外的1×1卷积层来将输入变换成需要的形状后再做相加运算。

  • 两种Residual
    经典卷积神经网络详解（AlexNet、VGG、NiN、GoogLeNet、ResNet、DenseNet、CSPNet、Darknet、EfficientNet、SqueezeNet..）_第35张图片
    左侧残差结构称为 BasicBlock (上文刚介绍过),右侧残差结构称为 Bottleneck
    BottleNeck的结构：
    （1）其中第一层的1× 1的卷积核的作用是对特征矩阵进行降维操作，将特征矩阵的深度由256降为64;
    第三层的1× 1的卷积核是对特征矩阵进行升维操作，将特征矩阵的深度由64升成256。
    降低特征矩阵的深度主要是为了减少参数的个数。
    如果采用BasicBlock,参数的个数应该是：256×256×3×3×2=1179648
    采用Bottleneck，参数的个数是：1×1×256×64+3×3×64×64+1×1×256×64=69632
    （2）先降后升为了主分支上输出的特征矩阵和捷径分支上输出的特征矩阵形状相同，以便进行加法操作。

注：CNN参数个数 = 卷积核尺寸×卷积核深度 × 卷积核组数 = 卷积核尺寸 × 输入特征矩阵深度 × 输出特征矩阵深度

ResNet的代码实现

  • 残差块的实现如下：
import torch
from torch import nn
from torch.nn import functional as F
from d2l import torch as d2l

class Residual(nn.Module):  #@save
    def __init__(self, input_channels, num_channels,
                 use_1x1conv=False, strides=1):
        super().__init__()
        self.conv1 = nn.Conv2d(input_channels, num_channels,
                               kernel_size=3, padding=1, stride=strides)
        self.conv2 = nn.Conv2d(num_channels, num_channels,
                               kernel_size=3, padding=1)
        if use_1x1conv:
            self.conv3 = nn.Conv2d(input_channels, num_channels,
                                   kernel_size=1, stride=strides)
        else:
            self.conv3 = None
        self.bn1 = nn.BatchNorm2d(num_channels)
        self.bn2 = nn.BatchNorm2d(num_channels)

    def forward(self, X):
        Y = F.relu(self.bn1(self.conv1(X)))
        Y = self.bn2(self.conv2(Y))
        if self.conv3:
            X = self.conv3(X)
        Y += X
        return F.relu(Y)

如下图所示，此代码生成两种类型的网络： 一种是当use_1x1conv=False
时，应用ReLU非线性函数之前，将输入添加到输出。 另一种是当use_1x1conv=True时，添加通过1×1卷积调整通道和分辨率。

下面我们来查看输入和输出形状一致的情况。

blk = Residual(3,3)
X = torch.rand(4, 3, 6, 6)
Y = blk(X)
Y.shape
# torch.Size([4, 3, 6, 6])

我们也可以在增加输出通道数的同时，减半输出的高和宽。

blk = Residual(3,6, use_1x1conv=True, strides=2)
blk(X).shape
# torch.Size([4, 6, 3, 3])
  • ResNet模型

ResNet的前两层跟之前介绍的GoogLeNet中的一样： 在输出通道数为64、步幅为2的7×7卷积层后，接步幅为2的3×3的最大汇聚层。 不同之处在于ResNet每个卷积层后增加了批量规范化层。

b1 = nn.Sequential(nn.Conv2d(1, 64, kernel_size=7, stride=2, padding=3),
                   nn.BatchNorm2d(64), nn.ReLU(),
                   nn.MaxPool2d(kernel_size=3, stride=2, padding=1))

GoogLeNet在后面接了4个由Inception块组成的模块。 ResNet则使用4个由残差块组成的模块，每个模块使用若干个同样输出通道数的残差块。 第一个模块的通道数同输入通道数一致。 由于之前已经使用了步幅为2的最大汇聚层，所以无须减小高和宽。 之后的每个模块在第一个残差块里将上一个模块的通道数翻倍，并将高和宽减半。

下面我们来实现这个模块。注意，我们对第一个模块做了特别处理。

def resnet_block(input_channels, num_channels, num_residuals,
                 first_block=False):
    blk = []
    for i in range(num_residuals):
        if i == 0 and not first_block:
            blk.append(Residual(input_channels, num_channels,use_1x1conv=True, strides=2))
        else:
            blk.append(Residual(num_channels, num_channels))
    return blk

接着在ResNet加入所有残差块，这里每个模块使用2个残差块。

b2 = nn.Sequential(*resnet_block(64, 64, 2, first_block=True))
b3 = nn.Sequential(*resnet_block(64, 128, 2))
b4 = nn.Sequential(*resnet_block(128, 256, 2))
b5 = nn.Sequential(*resnet_block(256, 512, 2))

最后，与GoogLeNet一样，在ResNet中加入全局平均汇聚层，以及全连接层输出。

net = nn.Sequential(b1, b2, b3, b4, b5,
                    nn.AdaptiveAvgPool2d((1,1)),
                    nn.Flatten(), nn.Linear(512, 10))

每个模块有4个卷积层（不包括恒等映射的1×1卷积层）。 加上第一个7×7
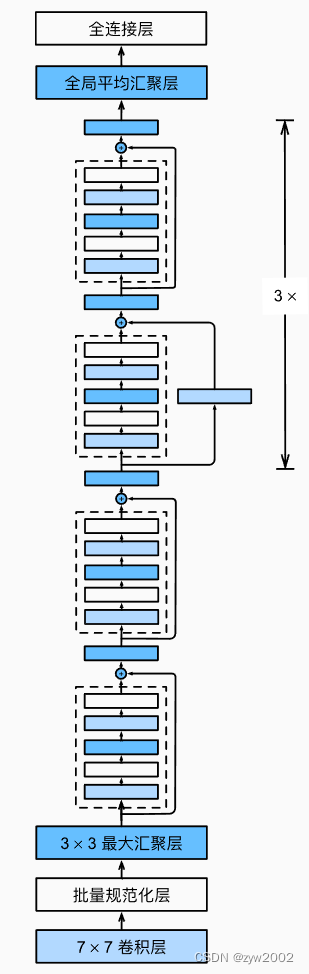
卷积层和最后一个全连接层，共有18层。 因此，这种模型通常被称为ResNet-18。 通过配置不同的通道数和模块里的残差块数可以得到不同的ResNet模型，例如更深的含152层的ResNet-152。 虽然ResNet的主体架构跟GoogLeNet类似，但ResNet架构更简单，修改也更方便。这些因素都导致了ResNet迅速被广泛使用。 下图描述了完整的ResNet-18。

经典卷积神经网络详解（AlexNet、VGG、NiN、GoogLeNet、ResNet、DenseNet、CSPNet、Darknet、EfficientNet、SqueezeNet..）_第36张图片

在训练ResNet之前，让我们观察一下ResNet中不同模块的输入形状是如何变化的。 在之前所有架构中，分辨率降低，通道数量增加，直到全局平均汇聚层聚集所有特征。

X = torch.rand(size=(1, 1, 224, 224))
for layer in net:
    X = layer(X)
    print(layer.__class__.__name__,'output shape:\t', X.shape)

Sequential output shape:     torch.Size([1, 64, 56, 56])
Sequential output shape:     torch.Size([1, 64, 56, 56])
Sequential output shape:     torch.Size([1, 128, 28, 28])
Sequential output shape:     torch.Size([1, 256, 14, 14])
Sequential output shape:     torch.Size([1, 512, 7, 7])
AdaptiveAvgPool2d output shape:      torch.Size([1, 512, 1, 1])
Flatten output shape:        torch.Size([1, 512])
Linear output shape:         torch.Size([1, 10])
  • 训练模型

同之前一样，我们在Fashion-MNIST数据集上训练ResNet。

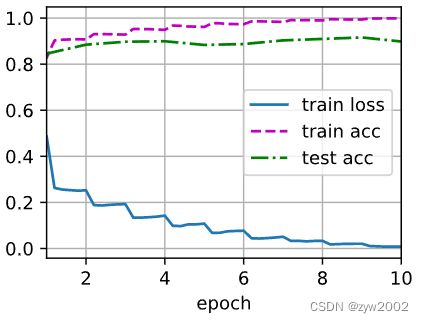
lr, num_epochs, batch_size = 0.05, 10, 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size, resize=96)
d2l.train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())

loss 0.011, train acc 0.997, test acc 0.915
4701.1 examples/sec on cuda:0

经典卷积神经网络详解（AlexNet、VGG、NiN、GoogLeNet、ResNet、DenseNet、CSPNet、Darknet、EfficientNet、SqueezeNet..）_第37张图片

  • 小结
    • 学习嵌套函数（nested function）是训练神经网络的理想情况。在深层神经网络中，学习另一层作为恒等映射（identity function）较容易（尽管这是一个极端情况）。
    • 残差映射可以更容易地学习同一函数，例如将权重层中的参数近似为零。
    • 利用残差块（residual blocks）可以训练出一个有效的深层神经网络：输入可以通过层间的残余连接更快地向前传播。
    • 残差网络（ResNet）对随后的深层神经网络设计产生了深远影响。

DenseNet: 稠密连接网络 （2017）

DenseNet 概述

Paper : 《Densely Connected Convolutional Networks》
Code: densenet.py

回想一下任意函数的泰勒展开式（Taylor expansion），它把这个函数分解成越来越高阶的项。在x接近0时，

f ( x ) = f ( 0 ) + f ′ ( 0 ) x + f ′ ′ ( 0 ) 2 ! x 2 + f ′ ′ ′ ( 0 ) 3 ! x 3 + … f(x)=f(0)+f^{\prime}(0) x+\frac{f^{\prime \prime}(0)}{2 !} x^2+\frac{f^{\prime \prime \prime}(0)}{3 !} x^3+\ldots f(x)=f(0)+f′(0)x+2!f′′(0)​x2+3!f′′′(0)​x3+…

同样, ResNet将函数展开为

f ( x ) = x + g ( x ) f(\mathbf{x})=\mathbf{x}+g(\mathbf{x}) f(x)=x+g(x)

也就是说，ResNet将 f f f分解为两部分：一个简单的线性项和一个复杂的非线性项。 那么再向前拓展一步，如果我们想将 f f f 拓展成超过两部分的信息呢？ 一种方案便是DenseNet。

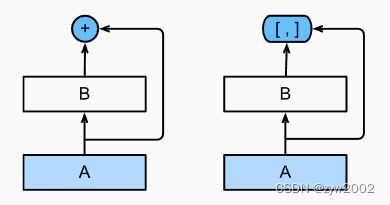
经典卷积神经网络详解（AlexNet、VGG、NiN、GoogLeNet、ResNet、DenseNet、CSPNet、Darknet、EfficientNet、SqueezeNet..）_第38张图片

如图所示，ResNet和DenseNet的关键区别在于，DenseNet输出是连接（用图中的[,]表示）而不是如ResNet的简单相加。 因此，在应用越来越复杂的函数序列后，我们执行从x到其展开式的映射：

x → [ x , f 1 ( x ) , f 2 ( [ x , f 1 ( x ) ] ) , f 3 ( [ x , f 1 ( x ) , f 2 ( [ x , f 1 ( x ) ] ) ] ) , … ] \mathbf{x} \rightarrow\left[\mathbf{x}, f_1(\mathbf{x}), f_2\left(\left[\mathbf{x}, f_1(\mathbf{x})\right]\right), f_3\left(\left[\mathbf{x}, f_1(\mathbf{x}), f_2\left(\left[\mathbf{x}, f_1(\mathbf{x})\right]\right)\right]\right), \ldots\right] x→[x,f1​(x),f2​([x,f1​(x)]),f3​([x,f1​(x),f2​([x,f1​(x)])]),…]

最后，将这些展开式结合到多层感知机中，再次减少特征的数量。 实现起来非常简单：我们不需要添加术语，而是将它们连接起来。 DenseNet这个名字由变量之间的“稠密连接”而得来，最后一层与之前的所有层紧密相连。 稠密连接如下图所示。

经典卷积神经网络详解（AlexNet、VGG、NiN、GoogLeNet、ResNet、DenseNet、CSPNet、Darknet、EfficientNet、SqueezeNet..）_第39张图片

稠密网络主要由2部分构成：稠密块（dense block）和过渡层（transition layer）。 前者定义如何连接输入和输出，而后者则控制通道数量，使其不会太复杂。

DenseNet 的网络结构

  • DenseNet和Conv、ResNet的对比
  1. 在标准的卷积网络中，输入图像经过多次卷积并获得高层特征。
    经典卷积神经网络详解（AlexNet、VGG、NiN、GoogLeNet、ResNet、DenseNet、CSPNet、Darknet、EfficientNet、SqueezeNet..）_第40张图片
    网络在第 l l l层的输出为：
    x l = H l ( x l − 1 ) x_l=H_l(x_{l-1}) xl​=Hl​(xl−1​)
    其中 H l ( ⋅ ) H_l(\cdot) Hl​(⋅) 代表的是非线性转换函数，它是一个组合操作，其可能包括一系列的BN(Batch Normalization),RELU,Pooling 以及Conv操作。
  2. 在ResNet中，提出了恒等映射（ identity mapping）,使用了元素加法(Element-wise addition)。有助于训练过程中的梯度的反向传播，从而能够训练出更深的网络。
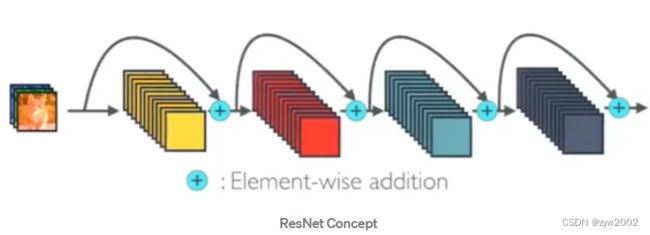
    经典卷积神经网络详解（AlexNet、VGG、NiN、GoogLeNet、ResNet、DenseNet、CSPNet、Darknet、EfficientNet、SqueezeNet..）_第41张图片
    对于ResNet, 增加了来自上一层的输入：
    x l = H l ( x l − 1 + x l − 1 ) x_l=H_l(x_{l-1}+x_{l-1}) xl​=Hl​(xl−1​+xl−1​)
  3. 在DenseNet中： 采用了密集连接的机制，即相互连接所有的层，每个层都会与前面所有的层在通道的维度上连接在一起（Channel-wise concatenation）, 实现特征重用，作为下一层的输入。这样不但减缓了梯度消失的现象，也使其可以在参数和计算量更少的情况下实现比ResNet更优的性能。
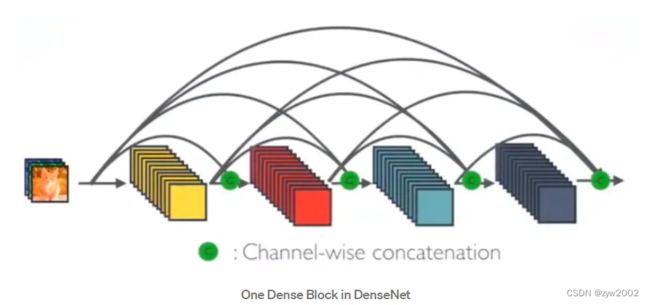
    经典卷积神经网络详解（AlexNet、VGG、NiN、GoogLeNet、ResNet、DenseNet、CSPNet、Darknet、EfficientNet、SqueezeNet..）_第42张图片
    在DenseNet中，会连接前面所有层作为输入：
    x l = H l ( [ x 0 , x 1 , . . . . x l − 1 ] ) x_l=H_l([x_0,x_1,....x_{l-1}]) xl​=Hl​([x0​,x1​,....xl−1​])
    下图展示了前向传播过程中的连接概念: 特征传递的方式是直接将前面所有层的特征Concat后传到下一层，而不是前面层都要有一个箭头指向后面的所有层。
    经典卷积神经网络详解（AlexNet、VGG、NiN、GoogLeNet、ResNet、DenseNet、CSPNet、Darknet、EfficientNet、SqueezeNet..）_第43张图片

DenseNet的网络结构
DenseNet的密集连接方式需要特征图大小保持一致，所以DenseNet网络中使用的是DenseBlock+Transition 的结构。
经典卷积神经网络详解（AlexNet、VGG、NiN、GoogLeNet、ResNet、DenseNet、CSPNet、Darknet、EfficientNet、SqueezeNet..）_第44张图片
DenseBlock 是包含很多层的模块，在每个dense block中，特征映射的大小是相同的，因此它们可以很容易地concat在一起。层（dense layer）与层之间采用的是密集连接的方式。
Transition Layer 1×1 Conv和2×2 average pooling被用作两个相邻dense block之间的过渡层（Transition Layer）。
在最后一个dense block的末尾，执行全局平均池化，然后附加一个softmax分类器。

  • Dense Block
    在DenseBlock中，各个层的特征图大小一致，可以在通道（channel）维度上连接。DenseBlock中的非线性组合函数 H l ( ⋅ ) H_l(\cdot) Hl​(⋅)采用的是 BN+ ReLU + 3x3 Conv 。输出是一个k个输出通道的特征图。
    x 5 = h 5 ( [ x 0 , x 1 , x 2 , x 3 , x 4 ] ) x_5=h_5([x_0,x_1,x_2,x_3,x_4]) x5​=h5​([x0​,x1​,x2​,x3​,x4​])。
    假定输入层的通道数是 k 0 k_0 k0​,DenseBlock中各个层卷积之后均输出 k k k个特征图，即得到的特征图的通道数为 k k k，那么l层输入的通道数为 k 0 ​ + ( l − 1 ) k k_0​+(l−1)k k0​​+(l−1)k, 我们将 k k k称之为网络的增长率（growth rate）。
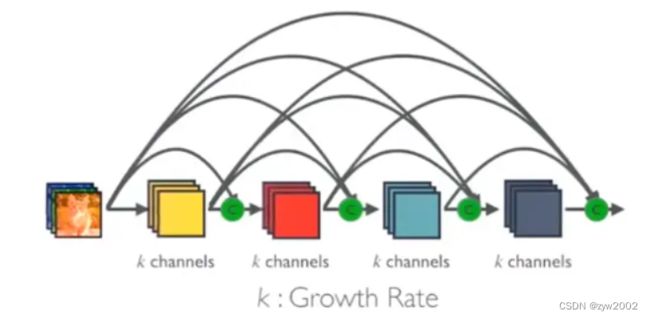
    经典卷积神经网络详解（AlexNet、VGG、NiN、GoogLeNet、ResNet、DenseNet、CSPNet、Darknet、EfficientNet、SqueezeNet..）_第45张图片
    因为每一层都接受前面所有层的特征图，即特征传递方式是直接将前面所有层的特征concat后传到下一层，一般情况下使用较小的K（比如12），要注意这个K的实际含义就是这层新提取出的特征。
    Dense Block采用了激活函数在前、卷积层在后的顺序，即BN-ReLU-Conv的顺序，这种方式也被称为pre-activation。通常的模型relu等激活函数处于卷积conv、批归一化batchnorm之后，即Conv-BN-ReLU，也被称为post-activation。这个想法是从Pre-Activation ResNet 中得来。作者证明，如果采用post-activation设计，性能会变差。

  • Transition Layer
    主要用来连接两个相邻的DenseBlock,并且降低特征图的大小。Transition Layer层包括一个1x1的卷积和2x2的AvgPooling，结构为BN+ReLU+1x1Conv+2x2AvgPooling

  • DenseNet-B (Bottleneck Layers)
    由于后面层的输入通道数会非常大，DenseBlock内部可以采用bottleneck Layers来减少为了减少模型的复杂度和大小，主要是原有的结构中增加1x1 Conv，BN+ReLU+1x1Conv+BN+ReLU+3x3Conv,
    这种结构也称作DenseNet-B 结构。
    其中1x1 Conv的作用是固定输出通道数，达到降维的作用，1×1卷积输出的通道数通常是GrowthRate的4倍。即把上一层输入的 l × k l\times k l×k个通道数减少成 4 × k 4 \times k 4×k 个通道数。从而降低特征数量，提升计算效率。
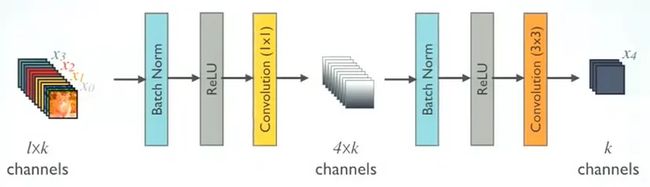
    经典卷积神经网络详解（AlexNet、VGG、NiN、GoogLeNet、ResNet、DenseNet、CSPNet、Darknet、EfficientNet、SqueezeNet..）_第46张图片
    当几十个Bottleneck相连接时，concat后的通道数会增加到上千，如果不增加1×1的卷积来降维，后续3×3卷积所需的参数量会急剧增加。
    比如，输入通道数 64 64 64，增长率 K = 32 K=32 K=32，经过 15 15 15个Bottleneck，通道数输出为 64 + 15 × 32 = 544 64+15\times32=544 64+15×32=544，
    如果不使用1×1卷积，第 16 16 16个Bottleneck层参数量是 3 × 3 × 544 × 32 = 156672 3\times3\times544\times32=156672 3×3×544×32=156672，
    如果使用1×1卷积，第 16 16 16个Bottleneck层参数量是 1 × 1 × 544 × 128 + 3 × 3 × 128 × 32 = 106496 1\times1\times544\times128+3\times3\times128\times32=106496 1×1×544×128+3×3×128×32=106496，可以看到参数量大大降低。

  • DenseNet-C(Transition Layers)
    在一个包含有m个特征图的dense block, Transition Layer产生 θ m \theta m θm 个特征图，其中 θ \theta θ 被看做是压缩系数。
    当 θ = 1 \theta =1 θ=1 时，通过过渡层后特征映射数量保持不变。当 θ < 1 \theta <1 θ<1 时，就被称为DenseNet-C, 在实验中选取的是 θ = 0.5 \theta=0.5 θ=0.5

  • DenseNet-BC (Further Compression)
    当同时采用了bottleneck和transition layer,且 θ < 1 \theta <1 θ<1, 这样的模型被称作DenseNet-BC。

Denseblock 优缺点

  • 优点：
    （1）更强的梯度流动
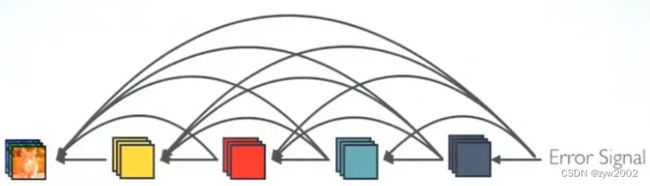
    经典卷积神经网络详解（AlexNet、VGG、NiN、GoogLeNet、ResNet、DenseNet、CSPNet、Darknet、EfficientNet、SqueezeNet..）_第47张图片
    1. 由于密集连接方式，DenseNet促进了梯度的反向传播，使得网络更容易训练。由于每层可以直达最后的误差信号，实现了隐式的“deep supervision”。误差信号可以很容易地传播到较早的层，所以较早的层可以从最终分类层获得直接监督。
    2. 减轻了vanishing-gradient（梯度消失） 过梯度消失问题在网络深度越深的时候越容易出现，原因就是输入信息和梯度信息在很多层之间传递导致的，而现在这种dense connection相当于每一层都直接连接input和loss，因此就可以减轻梯度消失现象，这样更深网络不是问题。

（2）减少参数与提升计算效率
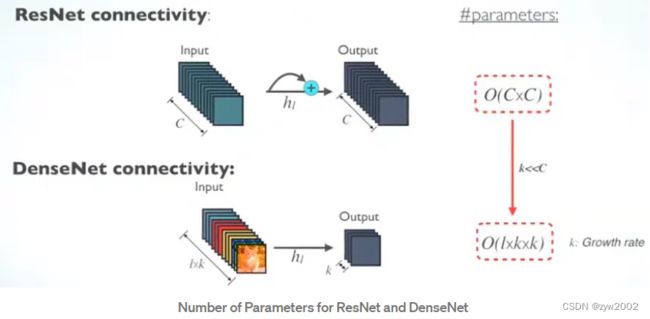
经典卷积神经网络详解（AlexNet、VGG、NiN、GoogLeNet、ResNet、DenseNet、CSPNet、Darknet、EfficientNet、SqueezeNet..）_第48张图片
对于每一层，ResNet中的参数数量与 C × C C×C C×C成正比，DenseNet中的参数数量与 l × k × k l\times k\times k l×k×k成正比。
由于k远小于C, 因此DenseNet 比 ResNet要小很多。

(3) 更多样化的特征
经典卷积神经网络详解（AlexNet、VGG、NiN、GoogLeNet、ResNet、DenseNet、CSPNet、Darknet、EfficientNet、SqueezeNet..）_第49张图片
由于DenseNet中的每一层都接收前面所有的层作为输入，因此特征更加多样化，往往具有更丰富的模式。

(4) 保存了低纬度的特征
经典卷积神经网络详解（AlexNet、VGG、NiN、GoogLeNet、ResNet、DenseNet、CSPNet、Darknet、EfficientNet、SqueezeNet..）_第50张图片
在标准的卷积网络中，最终输出只会利用提取最高层次的特征。
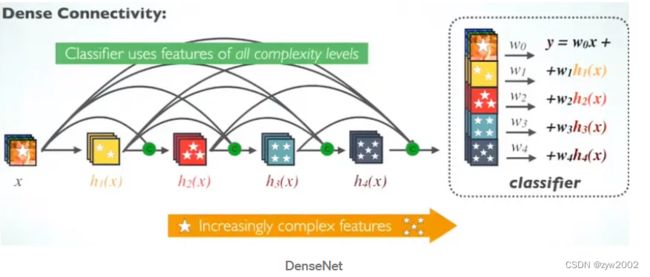
经典卷积神经网络详解（AlexNet、VGG、NiN、GoogLeNet、ResNet、DenseNet、CSPNet、Darknet、EfficientNet、SqueezeNet..）_第51张图片
而在DenseNet中，它使用了不同层次的特征，倾向于给出更平滑的决策边界。这也解释了为什么训练数据不足时DenseNet表现依旧良好。

  • 不足：
    DenseNet的不足在于由于需要进行多次Concatnate操作，数据需要被复制多次，显存容易增加得很快，需要一定的显存优化技术。另外，DenseNet是一种更为特殊的网络，ResNet则相对一般化一些，因此ResNet的应用范围更广泛。

DenseNet的代码实现

  • DenseBlock的实现
    DenseNet使用了ResNet改良版的“批量规范化、激活和卷积”架构。 我们首先实现一下这个架构。
import torch
from torch import nn
from d2l import torch as d2l

def conv_block(input_channels, num_channels):
    return nn.Sequential(
        nn.BatchNorm2d(input_channels), nn.ReLU(),
        nn.Conv2d(input_channels, num_channels, kernel_size=3, padding=1))

一个denseblock由多个卷积块组成，每个卷积块使用相同数量的输出通道。 然而，在前向传播中，我们将每个卷积块的输入和输出在通道维上连结。

class DenseBlock(nn.Module):
    def __init__(self, num_convs, input_channels, num_channels):
        super(DenseBlock, self).__init__()
        layer = []
        for i in range(num_convs):
            layer.append(conv_block(
                num_channels * i + input_channels, num_channels))
        self.net = nn.Sequential(*layer)

    def forward(self, X):
        for blk in self.net:
            Y = blk(X)
            # 连接通道维度上每个块的输入和输出
            X = torch.cat((X, Y), dim=1)
        return X

在下面的例子中，我们定义一个有2个输出通道数为10的DenseBlock。 使用通道数为3的输入时，我们会得到通道数为3+2×10=23的输出。 卷积块的通道数控制了输出通道数相对于输入通道数的增长，因此也被称为增长率（growth rate）。

blk = DenseBlock(2, 3, 10)
X = torch.randn(4, 3, 8, 8)
Y = blk(X)
Y.shape
  • Transition layer的实现
    由于每个稠密块都会带来通道数的增加，使用过多则会过于复杂化模型。 而过渡层可以用来控制模型复杂度。 它通过1×1卷积层来减小通道数，并使用步幅为2的平均汇聚层减半高和宽，从而进一步降低模型复杂度。
def transition_block(input_channels, num_channels):
    return nn.Sequential(
        nn.BatchNorm2d(input_channels), nn.ReLU(),
        nn.Conv2d(input_channels, num_channels, kernel_size=1),
        nn.AvgPool2d(kernel_size=2, stride=2))

对上一个例子中稠密块的输出使用通道数为10的过渡层。 此时输出的通道数减为10，高和宽均减半。

blk = transition_block(23, 10)
blk(Y).shape # torch.Size([4, 10, 4, 4])
  • DenseNet模型的实现

我们来构造DenseNet模型。DenseNet首先使用同ResNet一样的单卷积层和最大汇聚层。

b1 = nn.Sequential(
    nn.Conv2d(1, 64, kernel_size=7, stride=2, padding=3),
    nn.BatchNorm2d(64), nn.ReLU(),
    nn.MaxPool2d(kernel_size=3, stride=2, padding=1))

接下来，类似于ResNet使用的4个残差块，DenseNet使用的是4个稠密块。 与ResNet类似，我们可以设置每个稠密块使用多少个卷积层。 这里我们设成4，从而与 ResNet-18保持一致。 稠密块里的卷积层通道数（即增长率）设为32，所以每个稠密块将增加128个通道。

在每个模块之间，ResNet通过步幅为2的残差块减小高和宽，DenseNet则使用过渡层来减半高和宽，并减半通道数。

# num_channels为当前的通道数
num_channels, growth_rate = 64, 32
num_convs_in_dense_blocks = [4, 4, 4, 4]
blks = []
for i, num_convs in enumerate(num_convs_in_dense_blocks):
    blks.append(DenseBlock(num_convs, num_channels, growth_rate))
    # 上一个稠密块的输出通道数
    num_channels += num_convs * growth_rate
    # 在稠密块之间添加一个转换层，使通道数量减半
    if i != len(num_convs_in_dense_blocks) - 1:
        blks.append(transition_block(num_channels, num_channels // 2))
        num_channels = num_channels // 2

与ResNet类似，最后接上全局汇聚层和全连接层来输出结果。

net = nn.Sequential(
    b1, *blks,
    nn.BatchNorm2d(num_channels), nn.ReLU(),
    nn.AdaptiveAvgPool2d((1, 1)),
    nn.Flatten(),
    nn.Linear(num_channels, 10))
  • 训练模型
    由于这里使用了比较深的网络，本节里我们将输入高和宽从224降到96来简化计算。
lr, num_epochs, batch_size = 0.1, 10, 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size, resize=96)
d2l.train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())

loss 0.140, train acc 0.950, test acc 0.838
5569.1 examples/sec on cuda:0

经典卷积神经网络详解（AlexNet、VGG、NiN、GoogLeNet、ResNet、DenseNet、CSPNet、Darknet、EfficientNet、SqueezeNet..）_第52张图片

DenseNet小结

  • 在跨层连接上，不同于ResNet中将输入与输出相加，稠密连接网络（DenseNet）在通道维上连结输入与输出。
  • DenseNet的主要构建模块是稠密块和过渡层。
  • 在构建DenseNet时，我们需要通过添加过渡层来控制网络的维数，从而再次减少通道的数量。

Darknet-19 （2016）

Darknet-19 的概述

Paper : 《YOLO9000: Better, Faster, Stronger》
Code: AlexeyAB/darknet

Darknet-19 是Joseph Redmon 于2016年提出的。
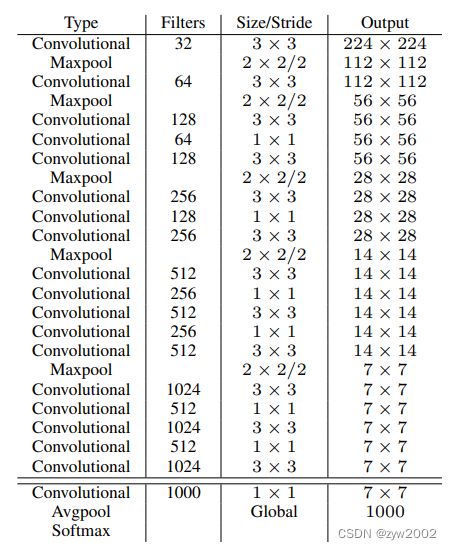
Darknet-19 是 YOLO v2 的 backbone。Darknet-19 总共有 19 层 conv 层， 5 个 maxpooling 层。Darknet-19 吸收了 VGG16, NIN 等网络的优点，网络结构小巧，但是性能强悍。

Darknet-19的网络结构

  • 实际输入为416 ∗ 416 416*416416∗416
  • 没有FC层，5次降采样(MaxPool)，19个卷积层
  • 使用Batch Normilazation来让训练更稳定，加速收敛，使model规范化。
  • 使用Global Average Pooling

经典卷积神经网络详解（AlexNet、VGG、NiN、GoogLeNet、ResNet、DenseNet、CSPNet、Darknet、EfficientNet、SqueezeNet..）_第53张图片

Darknet-53 （2018）

Darknet-53 的概述

Paper : YOLOv3: An Incremental Improvement
Code : pjreddie/darkne

Darknet-19 是Joseph Redmon 于2018年提出的。
Darknet-19 是 YOLO v3 的 backbone。Darknet-53 借鉴了 Resnet 的设计思想，引入了 shotcut 的概念。

Darknet-53的网络结构
Darknet53的结构如下图。左侧是 Darknet-53 的完整结构图，右侧是对左侧中的 Convolutional 层 和 Residual层的细节展示。
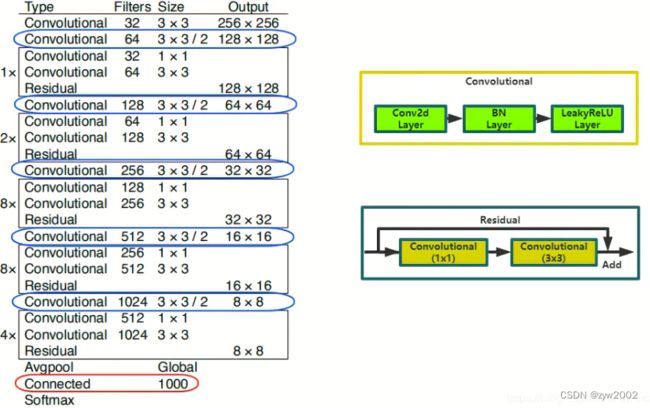
经典卷积神经网络详解（AlexNet、VGG、NiN、GoogLeNet、ResNet、DenseNet、CSPNet、Darknet、EfficientNet、SqueezeNet..）_第54张图片

Darknet-53 顾名思意，总共有 53 个卷积层，但是下面面的结构中只看到 52 个卷积层，其实 最后的 “Connected” 层也是卷积层（1x1 的卷积实现的类似 fc 的效果，所以也有资料把它称做 fc 层），“Connected” 层的具体参数如下。

[convolutional]
filters=1000
size=1
stride=1
pad=1
activation=linear

Darknet-53 输入 image size 为 256（没有 fc 层，显然可以随意修改输入 size），最后得到的 feature map size 为 8x8，stride 为 32（值得注意的是 5 次下采样，都不是通过 pooling 做的，而是通过 stride 为 2 的卷积层实现的，上图中蓝色框标出的位置，darknet-19 中是通过 max pooling）。

EfficientNetV1 (2019）

EfficientNetv1的概述

Paper :《EfficientNet: Rethinking Model Scaling for Convolutional Neural Networks》
Code :efficientnet_pytorch

  • EfficientNet的提出背景
    卷积神经网络精读提升的经验：
    1） 网络深度的增加。网络越深，学习到的特征越丰富、复杂。但太深容易造成梯度消失，导致训练困难。典型的如resnet,就是通过残差网络的堆叠，增加网络层数，以此来提升精度。
    2）网络宽度的增加。通过增加每层网络的特征层数，提取更多的特征，以此来提升精度，且容易训练。但光宽不深的话，学习不到深层次的特征，且要综合衡量计算量的问题。
    3）图像分辨率的增加。分辨率越高的图像，所能获取的信息越多，网络能得到 潜在的 更高细粒度的特征channel。但有瓶颈，且会增加计算量，分辨率太高，得不偿失。
  • EfficientNet的特点
    EfficientNet利用NAS(Neural Architecture Search)搜索技术，很好的平衡深度、宽度和分辨率这三个维度，通过一组固定的缩放系数统一缩放这三个维度。
    举例，如果我们需要使用 2 N 2^{\mathrm{N}} 2N 的计算机 资源，我们可以对网络深度放大 α N \alpha^{\mathrm{N}} αN ，对网络宽度放大 β N \beta^{\mathrm{N}} βN, 对分辨率放大 γ N \gamma^{\mathrm{N}} γN 。
    经典卷积神经网络详解（AlexNet、VGG、NiN、GoogLeNet、ResNet、DenseNet、CSPNet、Darknet、EfficientNet、SqueezeNet..）_第55张图片
    如上图，（a）是baseline基准网络。（b）是网络宽度的缩放。（c）是网络深度的缩放。（d）是分辨率的缩放。（e）是平衡综合网络深度，网络宽度，分辨率三个维度。
    其中，baseline基准网络是通过网络结构搜索得到，基于baseline基准网络进行放大得到的一系列网络就是EfficientNet网络。

EfficientNetv1的网络结构

  • MBConv结构
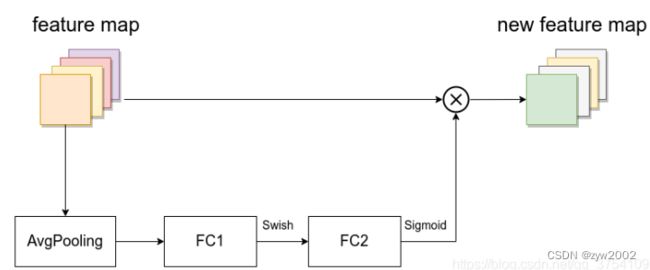
    MBConv其实就是MobileNetV3网络中的InvertedResidualBlock，但也有些许区别。一个是采用的激活函数不一样（EfficientNet的MBConv中使用的都是Swish激活函数），另一个是在每个MBConv中都加入了SE（Squeeze-and-Excitation）模块。
    经典卷积神经网络详解（AlexNet、VGG、NiN、GoogLeNet、ResNet、DenseNet、CSPNet、Darknet、EfficientNet、SqueezeNet..）_第56张图片
    如图所示，MBConv结构主要由一个1x1的普通卷积（升维作用，包含BN和Swish），一个kxk的Depthwise Conv卷积（包含BN和Swish）k的具体值可看EfficientNet-B0的网络框架主要有3x3和5x5两种情况，一个SE模块，一个1x1的普通卷积（降维作用，包含BN），一个Droupout层构成。
    搭建过程中还需要注意几点：
    第一个升维的1x1卷积层，它的卷积核个数是输入特征矩阵channel的n 倍，n∈{1,6}。
    当n = 1 时，不要第一个升维的1x1卷积层，即Stage2中的MBConv结构都没有第一个升维的1x1卷积层（这和MobileNetV3网络类似）。
    关于shortcut连接，仅当输入MBConv结构的特征矩阵与输出的特征矩阵shape相同时才存在（代码中可通过stride==1 and inputc_channels==output_channels条件来判断）。
    SE模块如下所示，由一个全局平均池化，两个全连接层组成。第一个全连接层的节点个数是输入该MBConv特征矩阵channels的1/4。且使用Swish激活函数。第二个全连接层的节点个数等于Depthwise Conv层输出的特征矩阵channels，且使用Sigmoid激活函数。
    经典卷积神经网络详解（AlexNet、VGG、NiN、GoogLeNet、ResNet、DenseNet、CSPNet、Darknet、EfficientNet、SqueezeNet..）_第57张图片
    Dropout层的dropout_rate在tensorflow的keras源码中对应的是drop_connect_rate后面会细讲（注意，在源码实现中只有使用shortcut的时候才有Dropout层）。

  • EfficientNet结构
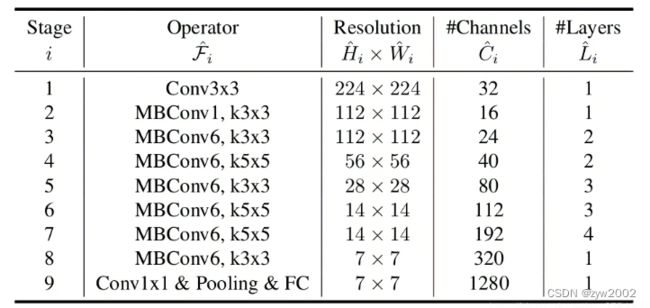
    下表为EfficientNet-B0的网络框架（B1-B7就是在B0的基础上修改Resolution，Channels以及Layers），可以看出网络总共分成了9个Stage
    Stage1就是一个卷积核大小为3x3步距为2的普通卷积层（包含BN和激活函数Swish）
    Stage2～Stage8都是在重复堆叠MBConv结构（最后一列的Layers表示该Stage重复MBConv结构多少次）
    Stage9由一个普通的1x1的卷积层（包含BN和激活函数Swish）一个平均池化层和一个全连接层组成。
    表格中每个MBConv后会跟一个数字1或6，这里的1或6就是倍率因子n即MBConv中第一个1x1的卷积层会将输入特征矩阵的channels扩充为n倍，其中k3x3或k5x5表示MBConv中Depthwise Conv所采用的卷积核大小。Channels表示通过该Stage后输出特征矩阵的Channels。
    经典卷积神经网络详解（AlexNet、VGG、NiN、GoogLeNet、ResNet、DenseNet、CSPNet、Darknet、EfficientNet、SqueezeNet..）_第58张图片

  • EfficientNet(B0-B7)参数
    经典卷积神经网络详解（AlexNet、VGG、NiN、GoogLeNet、ResNet、DenseNet、CSPNet、Darknet、EfficientNet、SqueezeNet..）_第59张图片
    input_size代表训练网络时输入网络的图像大小
    width_coefficient代表channel维度上的倍率因子，比如在 EfficientNetB0中Stage1的3x3卷积层所使用的卷积核个数是32，那么在B6中就是32 × 1.8 = 57.6 32 \times 1.8=57.632×1.8=57.6接着取整到离它最近的8的整数倍即56，其它Stage同理。
    depth_coefficient代表depth维度上的倍率因子（仅针对Stage2到Stage8），比如在EfficientNetB0中Stage7的
    ，那么在B6中就是4 × 2.6 = 10.4接着向上取整即11.
    drop_connect_rate是在MBConv结构中dropout层使用的drop_rate，在官方keras模块的实现中MBConv结构的drop_rate是从0递增到drop_connect_rate的（具体实现可以看下官方源码，注意，在源码实现中只有使用shortcut的时候才有Dropout层）。还需要注意的是，这里的Dropout层是Stochastic Depth，即会随机丢掉整个block的主分支（只剩捷径分支，相当于直接跳过了这个block）也可以理解为减少了网络的深度。具体可参考《Deep Networks with Stochastic Depth》这篇文章。
    dropout_rate是最后一个全连接层前的dropout层（在stage9的Pooling与FC之间）的dropout_rate。

EfficientNetV2 (2021)

EfficientNetv2的概述

Paper: 《EfficientNetV2: Smaller Models and Faster Training》
Code : efficientnetv2

  • EfficientNetV1中存在的问题
    训练图像的尺寸很大时，训练速度非常慢。
    在网络浅层中使用Depthwise convolutions速度会很慢。

  • EfficientNetV2中做出的贡献
    1）引入新的网络(EfficientNetV2)，该网络在训练速度以及参数数量上都优于先前的一些网络。
    2）提出了改进的渐进学习方法，该方法会根据训练图像的尺寸动态调节正则方法(例如dropout、data augmentation和mixup)。通过实验展示了该方法不仅能够提升训练速度，同时还能提升准确率。
    3）通过实验与先前的一些网络相比，训练速度提升11倍，参数数量减少为1/6.8

EfficientNetv2的网络结构
下表展示了作者使用NAS搜索得到的EfficientNetV2-S模型框架（注意，在源码中Stage6的输出Channels是等于256并不是表格中的272，Stage7的输出Channels是1280并不是表格中的1792，后续论文的版本会修正过来）。
相比与EfficientNetV1，主要有以下不同：

  1. 第一个不同点在于EfficientNetV2中除了使用到MBConv模块外，还使用了Fused-MBConv模块（主要是在网络浅层中使用）。
  2. 第二个不同点是EfficientNetV2会使用较小的expansion ratio（MBConv中第一个expand conv1x1或者Fused-MBConv中第一个expand conv3x3）比如4，在EfficientNetV1中基本都是6. 这样的好处是能够减少内存访问开销。
  3. 第三个不同点是EfficientNetV2中更偏向使用更小(3x3)的kernel_size，在EfficientNetV1中使用了很多5x5的kernel_size。通过下表可以看到使用的kernel_size全是3x3的，由于3x3的感受野是要比5x5小的，所以需要堆叠更多的层结构以增加感受野。
  4. 最后一个不同点是移除了EfficientNetV1中最后一个步距为1的stage（就是EfficientNetV1中的stage8），可能是因为它的参数数量过多并且内存访问开销过大。
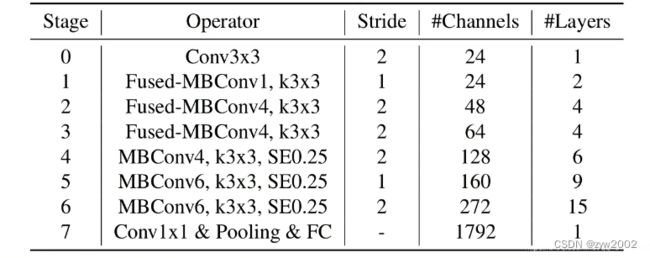
    经典卷积神经网络详解（AlexNet、VGG、NiN、GoogLeNet、ResNet、DenseNet、CSPNet、Darknet、EfficientNet、SqueezeNet..）_第60张图片
    通过上表可以看到EfficientNetV2-S分为Stage0到Stage7（EfficientNetV1中是Stage1到Stage9）。Operator表示在当前Stage中使用的模块：
  • Conv3x3就是普通的3x3卷积 + 激活函数（SiLU）+ BN
  • Fused-MBConv模块上面再讲EfficientNetV1存在问题章节有讲到过，模块名称后跟的1，4表示expansion ratio，k3x3表示kenel_size为3x3，下面是我自己重绘的结构图，注意当expansion ratio等于1时是没有expand conv的，还有这里是没有使用到SE结构的（原论文图中有SE）。注意当stride=1且输入输出Channels相等时才有shortcut连接。还需要注意的是，当有shortcut连接时才有Dropout层，而且这里的Dropout层是Stochastic Depth，即会随机丢掉整个block的主分支（只剩捷径分支，相当于直接跳过了这个block）也可以理解为减少了网络的深度。具体可参考《Deep Networks with Stochastic Depth》这篇文章。
    经典卷积神经网络详解（AlexNet、VGG、NiN、GoogLeNet、ResNet、DenseNet、CSPNet、Darknet、EfficientNet、SqueezeNet..）_第61张图片
    MBConv模块和EfficientNetV1中是一样的，其中模块名称后跟的4，6表示expansion ratio，SE0.25表示使用了SE模块，0.25表示SE模块中第一个全连接层的节点个数是输入该MBConv模块特征矩阵channels的1/4。
    注意当stride=1且输入输出Channels相等时才有shortcut连接。同样这里的Dropout层是Stochastic Depth。
    在这里插入图片描述
    Stride就是步距，注意每个Stage中会重复堆叠Operator模块多次，只有第一个Opertator模块的步距是按照表格中Stride来设置的，其他的默认都是1。 #Channels表示该Stage输出的特征矩阵的Channels，#Layers表示该Stage重复堆叠Operator的次数。

CSPNet：跨阶段局部网络（2020）

Paper :《CSPNET: A New Backbone that can Enhance Learning Capability of CNN》
Code : CrossStagePartialNetworks

Chien-Yao Wang等人在CVPR2019上发表的。文章提出了跨阶段局部网络(CrossStagePartialNetworks，CSPNet)，以缓解以往的工作需进行大量推理计算的问题。作者把这个问题归结为网络优化中的重复梯度信息。

  • CSP的设计方法
    Cross Stage Partial Network

DenseNet的网络结构
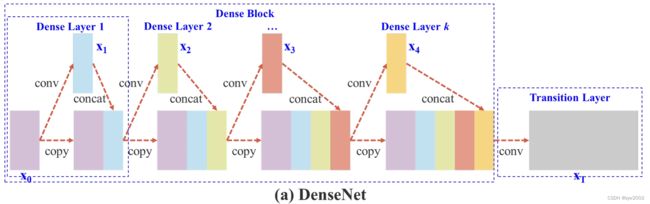
经典卷积神经网络详解（AlexNet、VGG、NiN、GoogLeNet、ResNet、DenseNet、CSPNet、Darknet、EfficientNet、SqueezeNet..）_第62张图片
上图为DenseNet单阶段结构的详细结构。DenseNet的每个阶段包含一个稠密块(Dense Block)和一个过渡层(Transition Layer)，每个稠密块由 k k k个稠密层(Dense Layer)组成。其中，第 l l l层接收所有先前的层 x 0 , x 1 , . . . , x l − 1 x_0, x_1,..., x_{l-1} x0​,x1​,...,xl−1​的特征图作为输入。

DenseNet的前向传播方程为：
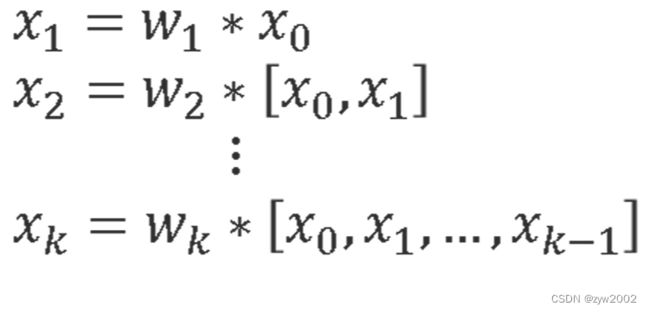
经典卷积神经网络详解（AlexNet、VGG、NiN、GoogLeNet、ResNet、DenseNet、CSPNet、Darknet、EfficientNet、SqueezeNet..）_第63张图片
其中 ∗ * ∗ 表示卷积运算符， w i w_i wi​和 x i x_i xi​ 分别表示第 i i i个稠密层的权值和输出。

DenseNet的权值更新方程为：
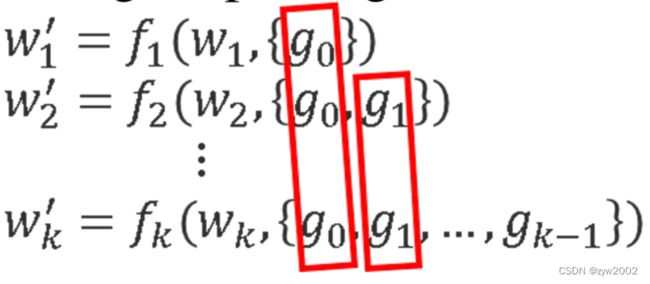
经典卷积神经网络详解（AlexNet、VGG、NiN、GoogLeNet、ResNet、DenseNet、CSPNet、Darknet、EfficientNet、SqueezeNet..）_第64张图片
其中 f f f 为权值更新函数， g i g_i gi​为传播到第 i i i个稠密层的梯度。我们可以发现大量的梯度信息被用来更新不同稠密层的权值。这将导致无差异的稠密层反复学习同样的梯度信息。

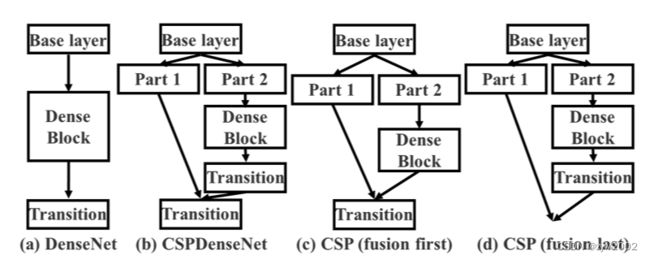
跨阶段局部DenseNet (Cross Stage Partial DenseNet)
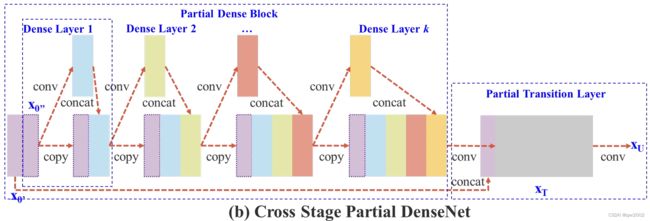
经典卷积神经网络详解（AlexNet、VGG、NiN、GoogLeNet、ResNet、DenseNet、CSPNet、Darknet、EfficientNet、SqueezeNet..）_第65张图片
提出的CSPDenseNet的单阶段的架构如上图所示。
CSPDenseNet的一个阶段由局部密集块(Partial Dense Block)和局部过渡层（Partial Transition Layer）组成。
在局部密集块中：把通道 x 0 = [ x 0 ′ , x 0 ′ ′ ] x_0=[x_0^{'},x_0^{''}] x0​=[x0′​,x0′′​]的基础层特征映射成两部分。其中 x 0 ′ x_0^{'} x0′​ 直接连接到阶段的末端， x 0 ′ ′ x_0^{''} x0′′​进入到下一个密集块。
在局部过渡层中：首先，Dense Layer K的输出 [ x 0 ′ ′ , x 1 , . . . , x k ] [x_0^{''},x_1,...,x_k] [x0′′​,x1​,...,xk​]将会进入到下一个过渡层。然后这个过渡层的输出 x T x_T xT​将和 x 0 ′ x_0^{'} x0′​相连，并进入到另一个过渡层，最终生成输出 x U x_U xU​

CSPDenseNet的前向传播方程为：
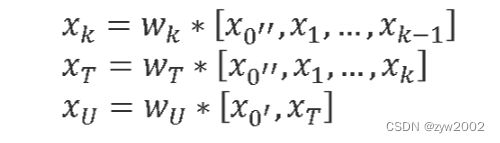
经典卷积神经网络详解（AlexNet、VGG、NiN、GoogLeNet、ResNet、DenseNet、CSPNet、Darknet、EfficientNet、SqueezeNet..）_第66张图片
CSPDenseNet的权值更新方程为：
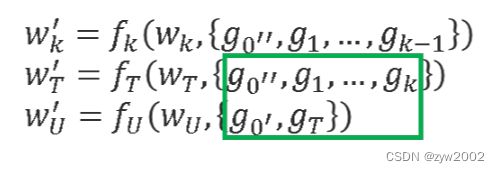
经典卷积神经网络详解（AlexNet、VGG、NiN、GoogLeNet、ResNet、DenseNet、CSPNet、Darknet、EfficientNet、SqueezeNet..）_第67张图片
从上面的权值更新方程可以看出，来自密集层的梯度是单独积分的。而且，没有经过密集层的特征图 x 0 ′ x_0^{'} x0′​ 也被单独积分。对于更新权值的梯度信息，两边不包含属于其他边的重复梯度信息。

总的来说，所提出的CSPDenseNet保留了DenseNet特性重用特性的优点，但同时通过截断梯度流防止了过多的重复梯度信息。该思想通过设计一种分层的特征融合策略来实现，并应用于局部过渡层。

局部密集块(Partial Dense Block)
设计局部稠密块的目的是：

  1. 增加梯度路径：通过分块归并策略，可以使梯度路径的数量增加一倍。由于采用了跨阶段策略，可以减轻使用显式特征图copy进行拼接所带来的弊端。
  2. 每一层的平衡计算：通常，DenseNet基层的通道数远大于生长速率。由于在局部稠密块中，参与稠密层操作的基础层通道仅占原始数据的一半，可以有效解决近一半的计算瓶颈;
  3. 减少内存流量：假设DenseNet中一个稠密块的基本特征图大小为 w × h × c w \times h \times c w×h×c ，增长率为 d d d (稠密块中每个稠密层输出特征图的通道数。)，共有 m m m 个 稠密层。则该密集块的CIO为 c × m + ( ( m 2 + m ) × d ) / 2 \mathrm{c} \times \mathrm{m}+\left(\left(\mathrm{m}^2+\mathrm{m}\right) \times \mathrm{d}\right) / 2 c×m+((m2+m)×d)/2 ，而局部密集块的CIO为 ( ( c × ((\mathrm{c} \times ((c× m ) + ( m 2 + m ) × d ) / 2 \left.\mathrm{m})+\left(\mathrm{m}^2+\mathrm{m}\right) \times \mathrm{d}\right) / 2 m)+(m2+m)×d)/2 。虽然m和 d d d 通常比c小得多，但单局部密集的块最多可以节省一半的 网络内存流量。

局部过渡层（Partial Transition Layer）
设计局部过渡层的目的是使梯度组合的差异最大。局部过渡层是一种层次化的特征融合机制，它利用梯度流的聚合策略来防止不同的层学习重复的梯度信息。在这里，作者设计了两个CSPDenseNet变体来展示这种梯度流截断是如何影响网络的学习能力的。

经典卷积神经网络详解（AlexNet、VGG、NiN、GoogLeNet、ResNet、DenseNet、CSPNet、Darknet、EfficientNet、SqueezeNet..）_第68张图片
上图中的 c 和 d 展示了两种不同的融合策略：

Fusion First：是将两部分生成的feature map进行拼接，然后进入过渡层。如果采用这种策略，将会损失大量的梯度信息。
Fusion Last：对于fusion last策略，来自稠密块的输出将经过过渡层，然后与来自Part1的feature map进行连接。如果采用这种策略，由于梯度流被截断，梯度信息将不会被重用。

应用CSPNet到其它网路
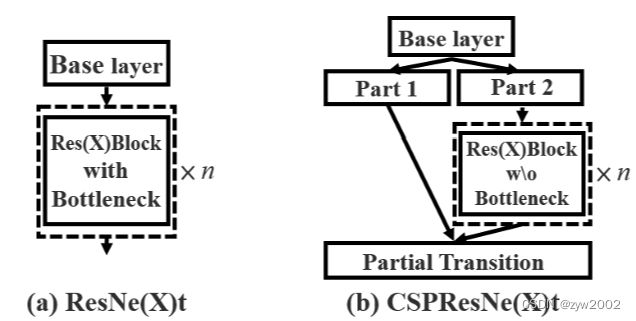
CSPNet也可以轻松地应用于ResNet 和 ResNeXt，其架构如下图所示。由于只有一半的特征通道通过Res（X）Blocks，因此就不再需要引入bottleneck了。当固定浮点运算（FLOP）时，这使理论上的内存访问成本（MAC）下限成为可能。
经典卷积神经网络详解（AlexNet、VGG、NiN、GoogLeNet、ResNet、DenseNet、CSPNet、Darknet、EfficientNet、SqueezeNet..）_第69张图片

  • Exact Fusion Model

看的准才能预测的准
作者建议使用EFM为每个锚点捕获合适的Field of View（FOV），以增强单阶段目标检测器的准确性。

对于分割任务，由于像素级标签通常不包含全局信息，因此通常更可取的是考虑使用更大的patches以获得更好的信息检索。但是，对于诸如图像分类和对象检测之类的任务，从图像级和边框框级标签观察时，某些关键信息可能会模糊不清。 Li等人发现，当从图像级标签中学习时，CNN经常会分散注意力并得出结论，这是两阶段目标检测器优于一级目标检测器的主要原因之一。

聚合特征金字塔
提出的EFM能够更好地聚合初始特征金字塔。 EFM基于YOLOv3 ，对每个真实物体精确分配了一个预选框。每个真值边界框对应于一个超过阈值IoU的预选框。如果预选框的大小等于网格单元的Field of View，则对于第s的网格单元，相应的边界框将由第s-1个scale的下界和第s+1个scale的上限局决定。因此，EFM会从三个比例尺中组合特征。

平衡计算开销
由于来自特征金字塔的串联特征图非常庞大，因此会引入大量的内存和计算成本。为了缓解该问题，我们采用了Maxout技术来压缩特征图。

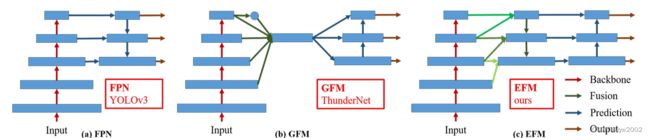
经典卷积神经网络详解（AlexNet、VGG、NiN、GoogLeNet、ResNet、DenseNet、CSPNet、Darknet、EfficientNet、SqueezeNet..）_第70张图片
上图描述了不同特征金字塔的融合策略
a) Feature Pyramid Network(FPN) : 把当前尺度和前一个尺度的特征融合
b) Global Fusion Model(GFM) : 从所有尺度上融合特征。
c) Exact Fusion Model(EFM) : 根据anchor的大小融合特征。

轻量化网络

深度学习领域内也在努力促使神经网络向小型化发展。在保证模型准确率的同时体积更小，速度更快。到了2016年直至现在，业内提出了SqueezeNet、ShuffleNet、MobileNet等轻量级网络模型。这些模型使移动终端、嵌入式设备运行神经网络模型成为可能。

SqueezeNet （2016）

SqueezeNet的概述

Paper : 《SqueezeNet: AlexNet-level accuracy with 50x fewer parameters and <0.5MB model size》
Code :DeepScale/SqueezeNet

Iandola, Forrest N等人在2016年提出了SqueezeNet, 考察了深度学习中除了精度之外的另一个重要因素：模型大小。
有两处值得学习的亮点：

  • 给出了一个分类精度接近AlexNet1的网络，模型缩小510倍
  • 归纳了缩小模型尺寸时的设计思路

使用以下三个策略来减少SqueezeNet设计参数
（1）使用1∗1卷积代替3∗3卷积：参数减少为原来的1/9
（2）减少输入通道数量：这一部分使用squeeze layers来实现
（3）将欠采样操作延后，可以给卷积层提供更大的激活图：更大的激活图保留了更多的信息，可以提供更高的分类准确率
其中，（1）和（2）可以显著减少参数数量，（3）可以在参数数量受限的情况下提高准确率

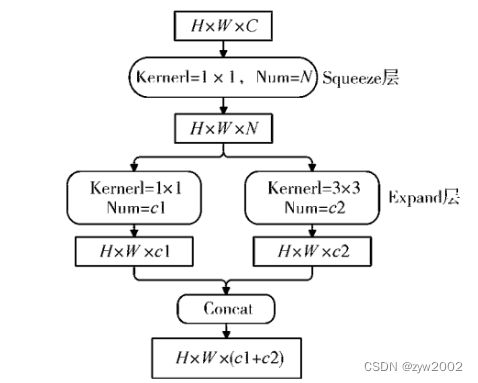
SqueezeNet的模型结构

  • 基础模块Filre
    经典卷积神经网络详解（AlexNet、VGG、NiN、GoogLeNet、ResNet、DenseNet、CSPNet、Darknet、EfficientNet、SqueezeNet..）_第71张图片

如上图，使用的基础模块称为fire。包含三个卷积层，步长均为1。分为squeeze和expand两部分，分别压缩和扩展数据的通道数。
expand部分中，两个不同核尺寸的结果通过串接层合并输出。

fire模块有三个可调参数:

  • N N N : squeeze部分， 1 × 1 1 \times 1 1×1 卷积层的通道数

  • c 1 \mathrm{c}_1 c1​ : expand部分, 1 × 1 1 \times 1 1×1 卷积层的通道数

  • c 2 \mathrm{c}_2 c2​ : expand部分, 3 × 3 3 \times 3 3×3 卷积层的通道数
    输入输出尺寸相同。输入通道数不限，输出通道数为 c 1 + c 2 \mathrm{c}_1+\mathrm{c}_2 c1​+c2​ 。 在本文提出的SqueezeNet结构中， c 1 = c 2 = 4 N \mathrm{c}_1=\mathrm{c}_2=4 \mathrm{N} c1​=c2​=4N 。

  • SqueezeNet的网络结构
    整个网络包含10层。

    1. 第1层为卷积层（蓝色），缩小输入图像，提取96维特征。
    2. 第2到9层为fire模块（红色），每个模块内部先减少通道数（squeeze）再增加通道数（expamd）。每两个模块之后，通道数会增加。
    3. 在1,4,8层之后加入降采样的max pooling（绿色），缩小一半尺寸。
    4. 第10层又是卷积层（蓝色），为小图的每个像素预测1000类分类得分
    5. 最后用一个全图average pooling（绿色）得到这张图的1000类得分，使用softmax函数归一化为概率。
      经典卷积神经网络详解（AlexNet、VGG、NiN、GoogLeNet、ResNet、DenseNet、CSPNet、Darknet、EfficientNet、SqueezeNet..）_第72张图片
      这是一个全卷积网络，避免了如今越来越不受待见的全连接层。由于最后一层提供了全图求平均操作，可以接受任意尺寸的输入。当然，输入还是需要归一化到大致相当的尺寸，保持统一尺度。
      全连接层的参数多，对性能提升帮助不大，现在往往被pooling代替。
      这个网络达到了和AlexNet相当的分类精度，但模型缩小了50倍。

SqueezeNet的小结

  • 使用 1 × 1 1 \times 1 1×1 卷积核代替 3 × 3 3 \times 3 3×3 卷积核，减少参数量；
  • 通过squeeze layer限制通道数量，减少参数量；
  • 借鉴Inception思想，将 1 × 1 1 \times 1 1×1 和 3 × 3 3 \times 3 3×3 卷积后结果进行concat；为了使其feature map的size相同， 3 × 3 3 \times 3 3×3 卷积核进行了padding；
  • 减少池化层，并将池化操作延后，给卷积层带来更大的激活层，保留更多地信息，提高准确率；
  • 使用全局平均池化代替全连接层;

MobileNetv1/2/3（2017,2018,2019）

MobileNet的概述

  • MobileNetv1

Paper :《MobileNets: Efficient Convolutional Neural Networks for Mobile Vision Applications》
Code : applications/mobilenet.py

传统卷积神经网络，内存需求大，计算量大，导致无法在移动设备以及嵌入式设备上运行。在准确率小幅降低的前提下大大减少模型参数和运算量（相比VGG16准确率降低0.9%，但是模型参数只有VGG的1/32）

Mobilenet这篇论文是Google针对手机等嵌入式设备提出的一种轻量级的深层神经网络，取名为MobileNets。个人感觉论文所做工作偏向于模型压缩方面，核心思想就是卷积核的巧妙分解，可以有效减少网络参数。
MobileNet V1引入了深度可分离卷积，作为传统卷积层的有效替代。深度可分卷积通过将空间滤波与特征生成机制分离开来，有效地分解了传统卷积。深度可分离卷积由两个单独的层定义:用于空间滤波的轻量级深度卷积和用于特征生成的1x1点卷积。
网络中的亮点：
(1) Depthwise Convolusion (大大减少运算量和参数数量)
(2) 增加超参数 α \alpha α和 β \beta β。 其中 α \alpha α 是卷积层中卷积核的个数， β \beta β 是控制输入图像的大小。这两个超参数是人为设置的，并不是训练得到的。

  • MobileNetV2
    相比于 MobileNet V1网络，准确率更高，模型更小。
    MobileNet V2引入了线性瓶颈和反向残留结构，以便通过利用问题的低级别性质来制造更有效的层结构。由一个1x1升维卷积，然后是DW卷积和一个1x1投影层来定义。当且仅当输入和输出具有相同数量的通道时，才使用残差结构连接输入和输出。该结构在输入和输出处保持了一个紧凑的表示，同时扩展到内部的高维特征空间，以增加非线性全通道转换的表现力。
    （1）Linear Bottlenecks: 引入了bottleneck结构。
    （2）Inverted Residuals(倒残差结构)： 将bottleneck结构变成了纺锤型，即resnet是先缩小为原来的1/4，再放大，他是放大到原来的6倍，再缩小。
    （3）并且去掉了Residual Block最后的ReLU。

  • MobileNetV3
    与MobileNet V2相比，MobileNet V3-Large在ImageNet分类上提高了3.2%，同时减少了20%的延迟。
    MobileNet V3-Small比具有同等延迟的MobileNet V2模型提高了6.6%。
    MobileNet V3-Large检测比MobileNet V2在COCO检测上的准确率高25%以上。
    MobileNet V3-Large LRASPP比MobileNet V2 R-ASPP在城市景观分割类似精度上快34%。
    MobileNetV3的亮点：
    （1）更新了Block: 在倒残差的基础上进行简单的改动 ，加入了SE模块，更新了激活函数。
    （2）使用NAS搜索参数
    （3）重新设计耗时层结构

MobileNet的网络结构

  • MobileNetv1的结构图
    经典卷积神经网络详解（AlexNet、VGG、NiN、GoogLeNet、ResNet、DenseNet、CSPNet、Darknet、EfficientNet、SqueezeNet..）_第73张图片
    整个网络不算平均池化层与softmax层，共28层；
    在整个网络结构中步长为2的卷积较有特点，卷积的同时充当下采样的功能；
    第一层之后的26层都为深度可分离卷积的重复卷积操作；
    每一个卷积层（含常规卷积、深度卷积、逐点卷积）之后都紧跟着批规范化和ReLU激活函数；
    最后一层全连接层不使用激活函数。

  • MobileNetv2的结构图
    经典卷积神经网络详解（AlexNet、VGG、NiN、GoogLeNet、ResNet、DenseNet、CSPNet、Darknet、EfficientNet、SqueezeNet..）_第74张图片
    MobileNetV2中主要引入线性瓶颈结构和反向残差结构。
    MobileNetV2网络模型中有共有17个Bottleneck层（每个Bottleneck包含两个逐点卷积层和一个深度卷积层），一个标准卷积层（conv），两个逐点卷积层（pw conv），共计有54层可训练参数层。MobileNetV2中使用线性瓶颈（Linear Bottleneck）和反向残差（Inverted Residuals）结构优化了网络，使得网络层次更深了，但是模型体积更小，速度更快了。

  • MobileNetv3的结构图
    MobileNetV3-Large
    经典卷积神经网络详解（AlexNet、VGG、NiN、GoogLeNet、ResNet、DenseNet、CSPNet、Darknet、EfficientNet、SqueezeNet..）_第75张图片
    MobileNetV3-Small
    经典卷积神经网络详解（AlexNet、VGG、NiN、GoogLeNet、ResNet、DenseNet、CSPNet、Darknet、EfficientNet、SqueezeNet..）_第76张图片
    MobileNetV3分为Large和Small两个版本，Large版本适用于计算和存储性能较高的平台，Small版本适用于硬件性能较低的平台。
    Large版本共有15个bottleneck层，一个标准卷积层，三个逐点卷积层。
    Small版本共有12个bottleneck层，一个标准卷积层，两个逐点卷积层。
    MobileNetV3中引入了5×5大小的深度卷积代替部分3×3的深度卷积。引入Squeeze-and-excitation（SE）模块和h-swish（HS）激活函数以提高模型精度。结尾两层逐点卷积不使用批规范化（Batch Norm），MobileNetV3结构图中使用NBN标识。
    经典卷积神经网络详解（AlexNet、VGG、NiN、GoogLeNet、ResNet、DenseNet、CSPNet、Darknet、EfficientNet、SqueezeNet..）_第77张图片
    网络结构上相对于MobileNetV2的结尾部分做了优化，去除三个高阶层，如上图所示。去除后减少了计算量和参数量，但是模型的精度并没有损失。
    值得一提的是，不论是Large还是Small版本，都是使用神经架构搜索（NAS）技术生成的网络结构。

ShffleNet （2017）

ShffleNet的概述

Paper :《ShuffleNet: An Extremely Efficient Convolutional Neural Network for Mobile Devices》
Code : models/shufflenetv1.py

ShuffleNet是旷视科技最近提出的一种计算高效的CNN模型，其和MobileNet和SqueezeNet等一样主要是想应用在移动端。所以，ShuffleNet的设计目标也是如何利用有限的计算资源来达到最好的模型精度，这需要很好地在速度和精度之间做平衡。ShuffleNet的核心是采用了两种操作：pointwise group convolution和channel shuffle，这在保持精度的同时大大降低了模型的计算量。目前移动端CNN模型主要设计思路主要是两个方面：模型结构设计和模型压缩。ShuffleNet和MobileNet一样属于前者，都是通过设计更高效的网络结构来实现模型变小和变快，而不是对一个训练好的大模型做压缩或者迁移。下面我们将详细讲述ShuffleNet的设计思路，网络结构及模型效果，最后使用Pytorch来实现ShuffleNet网络。

  • 逐点分组卷积
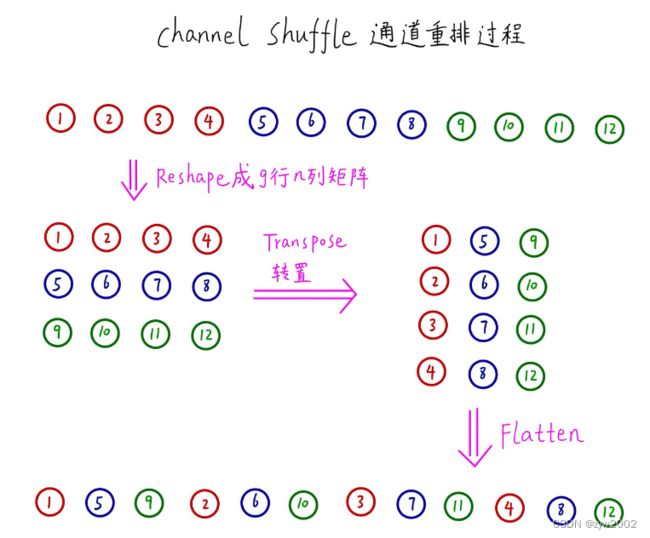
    逐点分组卷积就是将分组卷积核逐点卷积相结合，即表示卷积核大小为1*1的分组卷积。
  • 通道重排
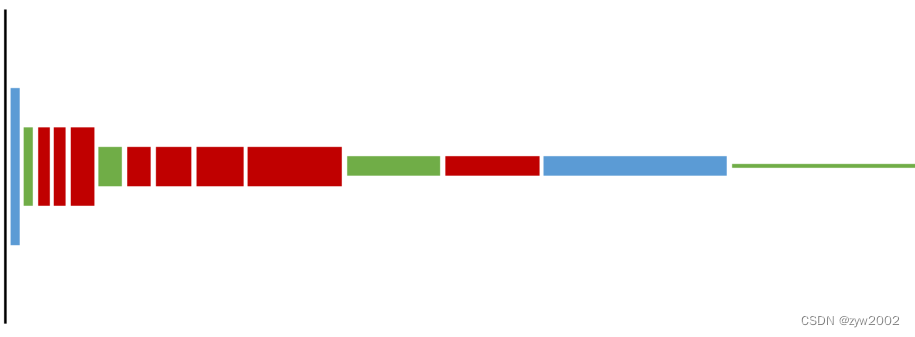
    逐点分组卷积后的效果如下：
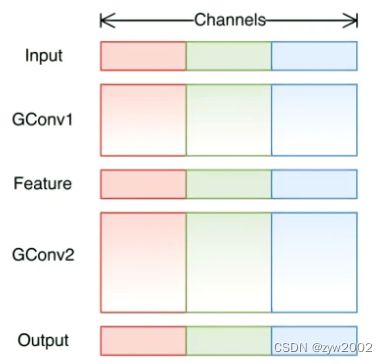
    经典卷积神经网络详解（AlexNet、VGG、NiN、GoogLeNet、ResNet、DenseNet、CSPNet、Darknet、EfficientNet、SqueezeNet..）_第78张图片
    这种分组因不同组之间没有任何联系，学习到的特征会非常有限，也很容易导致信息丢失

channel shuffle具体是怎么实现的呢？下图标绿框部分即为channel shuffle的操作，即从得到的特征图中提取出不同组别下的通道，并将他们组合在一起，最终channel shaffle完成后的结果如（c）中黄色虚线框所示。

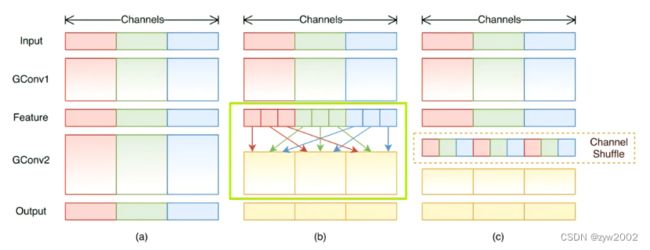经典卷积神经网络详解（AlexNet、VGG、NiN、GoogLeNet、ResNet、DenseNet、CSPNet、Darknet、EfficientNet、SqueezeNet..）_第79张图片上图中从绿框传变成黄色虚线框的过程即为channel shaffle通道重排过程，现将其分解出来，看看channel shaffle通道重排具体过程，如下图：

经典卷积神经网络详解（AlexNet、VGG、NiN、GoogLeNet、ResNet、DenseNet、CSPNet、Darknet、EfficientNet、SqueezeNet..）_第80张图片

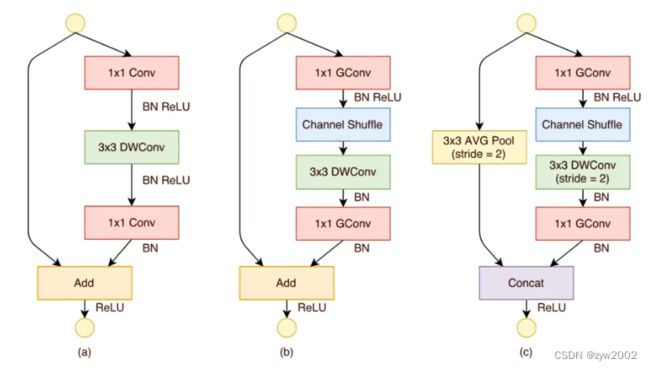
ShuffleNet的结构
 (a)是最原始的残差结构，(b)、（c）都是shuffleNet的单元结构。先来看看(a)是如何变成(b)的，首先是用逐点分组卷积代替了逐点卷积，同时在其后跟了一个channel shuffle操作，然后中间的3x3DWConv没有变化，最后的逐点卷积依旧换成了逐点分组卷积。(c)是用来降采样的，和(b)主要区别在shortcut分支中采用了3x3d的步长为2的AVG Pool、主分支中DWConv中的步长变成了2以及最后使用的是Concat而不是add,这样的结构会使输入图像尺寸减半，通道数翻倍。
经典卷积神经网络详解（AlexNet、VGG、NiN、GoogLeNet、ResNet、DenseNet、CSPNet、Darknet、EfficientNet、SqueezeNet..）_第81张图片

Xception （2017）

Xception的概述

Paper :《Xception: Deep Learning with Depthwise Separable Convolutions》
Code : research/deeplab

传统的卷积操作同时对输入的feature mapping的跨通道交互性（cross-channel correlations）、空间交互性（spatial correlations）进行了映射。

Inception系列结构着力于将上述过程进行分解，在一定程度上实现了跨通道相关性和空间相关性的解耦。

文章在Inception的基础上进行改进，使用深度可分离卷积（depthwise separate convolution）替代传统的Inception块，实现跨通道相关性和空间相关性的完全解耦。此外，文章还引入了残差连接，最终提出了Xception的网络结构。

传统Conv进行操作时，同时在输入的通道维度和空间维度进行了操作，跨通道相关性和空间相关性的耦合性很高。

例如，对于h*h*c的feature mapping，卷积核尺寸为s*s，但实际上卷积核尺寸为s*s*c。在进行一次卷积操作时，实际上对feature mapping中的一个s*s*c进行了信息融合，其中s*s为空间维度，c为通道维度。

  • InceptionV3中的原始模块
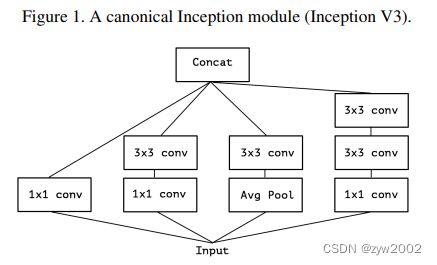
    经典卷积神经网络详解（AlexNet、VGG、NiN、GoogLeNet、ResNet、DenseNet、CSPNet、Darknet、EfficientNet、SqueezeNet..）_第82张图片
    Inception结构在一定程度上对跨通道相关性和空间相关性进行了解耦。
    先对feature mapping进行pointwise convolutions（1*1 Conv），以实现跨通道相关性的独立映射；然后进行分组卷积，将映射空间划分为若干个子空间，在子空间内进行卷积操作。
    可以发现的是，Inception结构在一定程度上实现了跨通道相关性和空间相关性的解耦，但并未实现完全解耦（子空间的卷积操作）。

  • 第一层简化
    Figure1 里基本都用了1 * 1 卷积进行降维，在这里可以说是在通道维度上进行处理。随后又处理了空间维度。
    简化了一下 变成了Figure2。
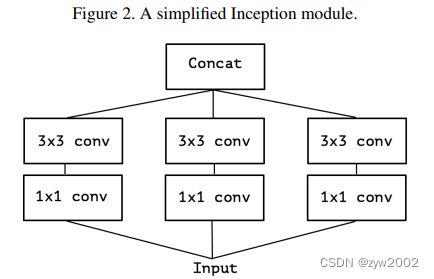
    经典卷积神经网络详解（AlexNet、VGG、NiN、GoogLeNet、ResNet、DenseNet、CSPNet、Darknet、EfficientNet、SqueezeNet..）_第83张图片

  • 第二层简化
    将所有的1 * 1 卷积合并到了一起，并且画了一条隔阂一样的东西，这里的意思就是每个3 * 3 的卷积取这条隔阂里的三分之一处理，且互不重合，假设1 * 1 之后生成了30个通道，则后面的3 * 3 卷积各处理其中的10个通道。
    经典卷积神经网络详解（AlexNet、VGG、NiN、GoogLeNet、ResNet、DenseNet、CSPNet、Darknet、EfficientNet、SqueezeNet..）_第84张图片
    多分支卷积中使用1*1 Conv进行降维等价于先进行1*1 Conv后在进行分组卷积。以简化版的Inception为例，Figure 3 给出了Inception的等价形式。

  • 最后的简化
    这里作者直接提出了 ‘Extreme’版本的处理方法，在之前是 假设了1 * 1 之后有30个通道，分给了三个卷积，每个卷积分到10个通道，而这里作者的 ‘Extreme’版本是 直接将这30个通道分给30个卷积去处理，即单独的对每一个空间信息做处理。
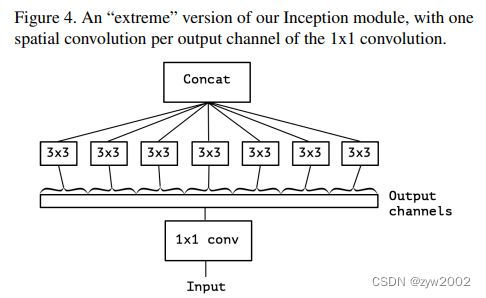
    经典卷积神经网络详解（AlexNet、VGG、NiN、GoogLeNet、ResNet、DenseNet、CSPNet、Darknet、EfficientNet、SqueezeNet..）_第85张图片

所以整体下来 ‘Extreme’ 版本 就是 1 * 1处理通道维度之间的信息，3 * 3 卷积处理每一个通道维度内的空间维度信息。

这个思想结构被称为 ，深度可分离卷积 （depthwise separable convolution & separable convolution），
depthwise convolution（空间维度的卷积，也就是长宽方向卷积）
pointwise convolution （通道维度的卷积）

Xception的结构
了Xception的具体结构如下图，其中共包括36层卷积，分为14个stage。
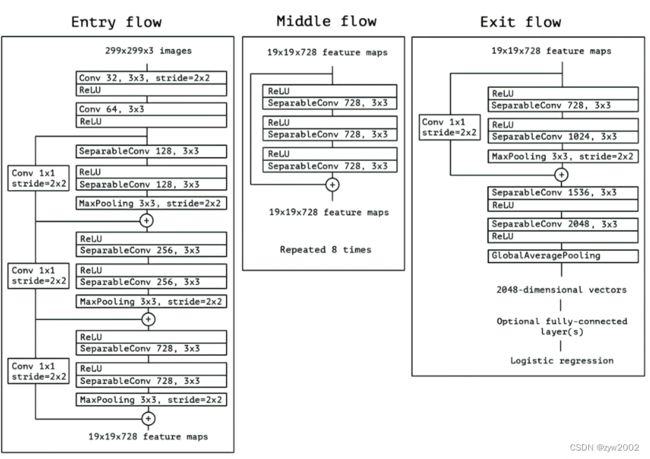
经典卷积神经网络详解（AlexNet、VGG、NiN、GoogLeNet、ResNet、DenseNet、CSPNet、Darknet、EfficientNet、SqueezeNet..）_第86张图片
Xception包含三个部分：输入部分，中间部分和结尾部分；其中所有卷积层和可分离卷积层后面都使用Batch Normalization处理，所有的可分离卷积层使用一个深度乘数1（深度方向并不进行扩充）

GhostNet(2020)

GhostNet的概述

Paper :《GhostNet: More Features from Cheap Operations》
Code : huawei-noah/Efficient-AI-Backbones

在优秀CNN模型中，特征图存在冗余是非常重要的，但是很少有人在模型结构设计上考虑特征图冗余问题（The redundancy in feature maps）。
GhostNet就从特征图冗余问题出发，提出一个仅通过少量计算（cheap operations）就能生成大量特征图的结构——Ghost Module。
Ghost Module通过怎么样的操作生成特征图呢？这个操作是，一系列线性操作（a series of linear transformations）
在这里，经过线性操作生成的特征图称为ghost feature maps，而被操作的特征图称为intrinsic feature maps。
即插即用：Ghost Module是一个即插即用模块，可以无缝衔接现有的CNN中。
采用Ghost Module组成的Ghost bottlenecks，设计出Ghost Net，在ILSVRC-2012上top1超过Mobilenet-V3，并且参数更少。

GhostNet的网络结构

  • GhostModule
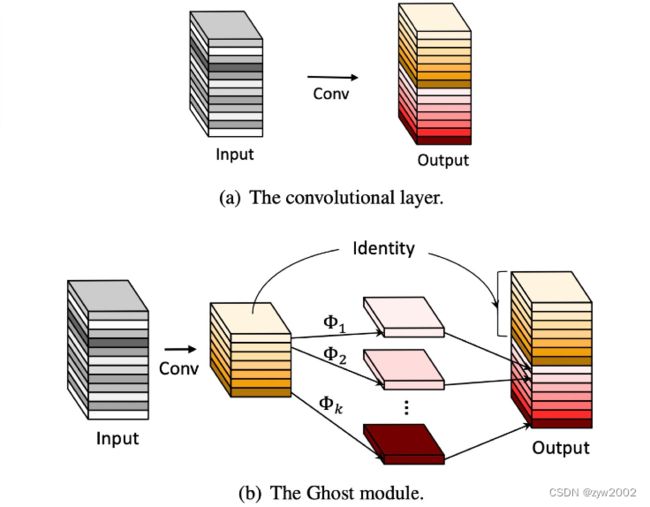
    经典卷积神经网络详解（AlexNet、VGG、NiN、GoogLeNet、ResNet、DenseNet、CSPNet、Darknet、EfficientNet、SqueezeNet..）_第87张图片
    通常的卷积如图2（a）所示，而Ghost Module则分为两步操作来获得与普通卷积一样数量的特征图（这里需要强调，是数量一样）。
    第一步：少量卷积（比如正常用32个卷积核，这里就用16个，从而减少一半的计算量）
    第二步：cheap operations，如图中的Φ表示，从问题3中可知，Φ是诸如3*3的卷积，并且是逐个特征图的进行卷积（Depth-wise convolutional）。

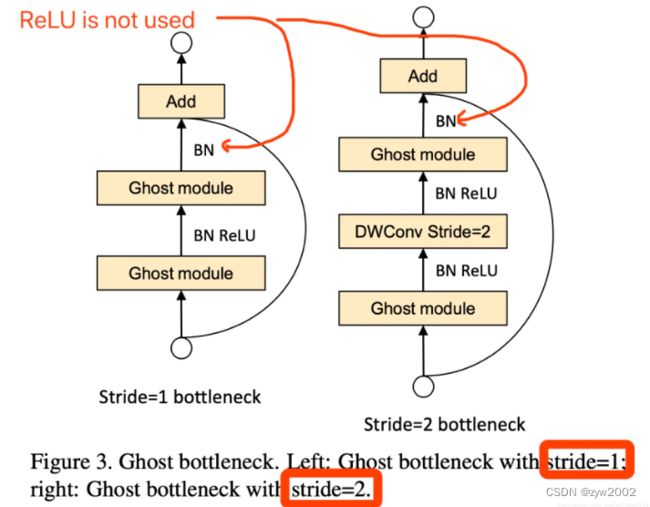
  • Ghost Bottlenecks
    Ghost Bottlenecks ，结构与ResNet的是类似的，并且与mobilenet-v2一样在第二个module之后不采用ReLU激活函数。
    左边是stride=1的Ghost Bottlenecks，右边是stride=2的Ghost Bottlenecks，目的是为了缩减特征图大小。
    经典卷积神经网络详解（AlexNet、VGG、NiN、GoogLeNet、ResNet、DenseNet、CSPNet、Darknet、EfficientNet、SqueezeNet..）_第88张图片

  • GhostNet
    Ghost Net结构与MobileNet-V3类似，并且用了SE结构，如下表，其中#exp表示G-bneck的第一个G-Module输出特征图数量
    经典卷积神经网络详解（AlexNet、VGG、NiN、GoogLeNet、ResNet、DenseNet、CSPNet、Darknet、EfficientNet、SqueezeNet..）_第89张图片

参考

DenseNet
https://towardsdatascience.com/review-densenet-image-classification-b6631a8ef803
https://blog.csdn.net/frighting_ing/article/details/121582735

CSPNet
https://blog.csdn.net/wjinjie/article/details/110952648

MobilNet
从MobileNet看轻量级神经网络的发展
MobileNet V1、V2、V3网络结构

你可能感兴趣的:(深度学习基础,深度学习,卷积神经网络)

  • 机器学习与深度学习间关系与区别 ℒℴѵℯ心·动ꦿ໊ོ꫞ 人工智能学习深度学习python
    一、机器学习概述定义机器学习（MachineLearning,ML）是一种通过数据驱动的方法，利用统计学和计算算法来训练模型，使计算机能够从数据中学习并自动进行预测或决策。机器学习通过分析大量数据样本，识别其中的模式和规律，从而对新的数据进行判断。其核心在于通过训练过程，让模型不断优化和提升其预测准确性。主要类型1.监督学习（SupervisedLearning）监督学习是指在训练数据集中包含输入
  • 将cmd中命令输出保存为txt文本文件 落难Coder Windowscmdwindow
    最近深度学习本地的训练中我们常常要在命令行中运行自己的代码，无可厚非，我们有必要保存我们的炼丹结果，但是复制命令行输出到txt是非常麻烦的，其实Windows下的命令行为我们提供了相应的操作。其基本的调用格式就是：运行指令>输出到的文件名称或者具体保存路径测试下，我打开cmd并且ping一下百度：pingwww.baidu.com>./data.txt看下相同目录下data.txt的输出：如果你再
  • 推荐3家毕业AI论文可五分钟一键生成！文末附免费教程！ 小猪包333 写论文人工智能AI写作深度学习计算机视觉
    在当前的学术研究和写作领域，AI论文生成器已经成为许多研究人员和学生的重要工具。这些工具不仅能够帮助用户快速生成高质量的论文内容，还能进行内容优化、查重和排版等操作。以下是三款值得推荐的AI论文生成器：千笔-AIPassPaper、懒人论文以及AIPaperPass。千笔-AIPassPaper千笔-AIPassPaper是一款基于深度学习和自然语言处理技术的AI写作助手，旨在帮助用户快速生成高质
  • AI大模型的架构演进与最新发展 季风泯灭的季节 AI大模型应用技术二人工智能架构
    随着深度学习的发展，AI大模型（LargeLanguageModels,LLMs）在自然语言处理、计算机视觉等领域取得了革命性的进展。本文将详细探讨AI大模型的架构演进，包括从Transformer的提出到GPT、BERT、T5等模型的历史演变，并探讨这些模型的技术细节及其在现代人工智能中的核心作用。一、基础模型介绍：Transformer的核心原理Transformer架构的背景在Transfo
  • [实践应用] 深度学习之模型性能评估指标 YuanDaima2048 深度学习工具使用深度学习人工智能损失函数性能评估pytorchpython机器学习
    文章总览：YuanDaiMa2048博客文章总览深度学习之模型性能评估指标分类任务回归任务排序任务聚类任务生成任务其他介绍在机器学习和深度学习领域，评估模型性能是一项至关重要的任务。不同的学习任务需要不同的性能指标来衡量模型的有效性。以下是对一些常见任务及其相应的性能评估指标的详细解释和总结。分类任务分类任务是指模型需要将输入数据分配到预定义的类别或标签中。以下是分类任务中常用的性能指标：准确率(
  • [实践应用] 深度学习之优化器 YuanDaima2048 深度学习工具使用pytorch深度学习人工智能机器学习python优化器
    文章总览：YuanDaiMa2048博客文章总览深度学习之优化器1.随机梯度下降（SGD）2.动量优化（Momentum）3.自适应梯度（Adagrad）4.自适应矩估计（Adam）5.RMSprop总结其他介绍在深度学习中，优化器用于更新模型的参数，以最小化损失函数。常见的优化函数有很多种，下面是几种主流的优化器及其特点、原理和PyTorch实现：1.随机梯度下降（SGD）原理:随机梯度下降通过
  • 生成式地图制图 Bwywb_3 深度学习机器学习深度学习生成对抗网络
    生成式地图制图（GenerativeCartography）是一种利用生成式算法和人工智能技术自动创建地图的技术。它结合了传统的地理信息系统（GIS）技术与现代生成模型（如深度学习、GANs等），能够根据输入的数据自动生成符合需求的地图。这种方法在城市规划、虚拟环境设计、游戏开发等多个领域具有应用前景。主要特点：自动化生成：通过算法和模型，系统能够根据输入的地理或空间数据自动生成地图，而无需人工逐
  • 吴恩达深度学习笔记(30)-正则化的解释 极客Array
    正则化（Regularization）深度学习可能存在过拟合问题——高方差，有两个解决方法，一个是正则化，另一个是准备更多的数据，这是非常可靠的方法，但你可能无法时时刻刻准备足够多的训练数据或者获取更多数据的成本很高，但正则化通常有助于避免过拟合或减少你的网络误差。如果你怀疑神经网络过度拟合了数据，即存在高方差问题，那么最先想到的方法可能是正则化，另一个解决高方差的方法就是准备更多数据，这也是非常
  • 个人学习笔记7-6：动手学深度学习pytorch版-李沐 浪子L 深度学习深度学习笔记计算机视觉python人工智能神经网络pytorch
    #人工智能##深度学习##语义分割##计算机视觉##神经网络#计算机视觉13.11全卷积网络全卷积网络（fullyconvolutionalnetwork，FCN）采用卷积神经网络实现了从图像像素到像素类别的变换。引入l转置卷积（transposedconvolution）实现的，输出的类别预测与输入图像在像素级别上具有一一对应关系：通道维的输出即该位置对应像素的类别预测。13.11.1构造模型下
  • 深度学习-点击率预估-研究论文2024-09-14速读 sp_fyf_2024 深度学习人工智能
    深度学习-点击率预估-研究论文2024-09-14速读1.DeepTargetSessionInterestNetworkforClick-ThroughRatePredictionHZhong,JMa,XDuan,SGu,JYao-2024InternationalJointConferenceonNeuralNetworks,2024深度目标会话兴趣网络用于点击率预测摘要：这篇文章提出了一种新
  • 计算机视觉中，Pooling的作用 Wils0nEdwards 计算机视觉人工智能
    在计算机视觉中，Pooling（池化）是一种常见的操作，主要用于卷积神经网络（CNN）中。它通过对特征图进行下采样，减少数据的空间维度，同时保留重要的特征信息。Pooling的作用可以归纳为以下几个方面：1.降低计算复杂度与内存需求Pooling操作通过对特征图进行下采样，减少了特征图的空间分辨率（例如，高度和宽度）。这意味着网络需要处理的数据量会减少，从而降低了计算量和内存需求。这对大型神经网络
  • 损失函数与反向传播 Star_. PyTorchpytorch深度学习python
    损失函数定义与作用损失函数(lossfunction)在深度学习领域是用来计算搭建模型预测的输出值和真实值之间的误差。1.损失函数越小越好2.计算实际输出与目标之间的差距3.为更新输出提供依据（反向传播)常见的损失函数回归常见的损失函数有：均方差（MeanSquaredError，MSE）、平均绝对误差（MeanAbsoluteErrorLoss，MAE）、HuberLoss是一种将MSE与MAE
  • 【深度学习】训练过程中一个OOM的问题，太难查了 weixin_40293999 深度学习深度学习人工智能
    现象：各位大佬又遇到过ubuntu的这个问题么？现象是在训练过程中，ssh上不去了，能ping通，没死机，但是ubunutu的pc侧的显示器，鼠标啥都不好用了。只能重启。问题原因：OOM了95G，尼玛！！！！pytorch爆内存了，然后journald假死了，在journald被watchdog干掉之后，系统就崩溃了。这种规模的爆内存一般，即使被oomkill了，也要卡半天的，确实会这样，能不能配
  • 云服务业界动态简报-20180128 Captain7
    一、青云青云QingCloud推出深度学习平台DeepLearningonQingCloud，包含了主流的深度学习框架及数据科学工具包，通过QingCloudAppCenter一键部署交付，可以让算法工程师和数据科学家快速构建深度学习开发环境，将更多的精力放在模型和算法调优。二、腾讯云1.腾讯云正式发布腾讯专有云TCE(TencentCloudEnterprise)矩阵，涵盖企业版、大数据版、AI
  • 机器学习VS深度学习 nfgo 机器学习
    机器学习（MachineLearning,ML）和深度学习（DeepLearning,DL）是人工智能（AI）的两个子领域，它们有许多相似之处，但在技术实现和应用范围上也有显著区别。下面从几个方面对两者进行区分：1.概念层面机器学习：是让计算机通过算法从数据中自动学习和改进的技术。它依赖于手动设计的特征和数学模型来进行学习，常用的模型有决策树、支持向量机、线性回归等。深度学习：是机器学习的一个子领
  • 大数据毕业设计hadoop+spark+hive知识图谱租房数据分析可视化大屏 租房推荐系统 58同城租房爬虫 房源推荐系统 房价预测系统 计算机毕业设计 机器学习 深度学习 人工智能 2401_84572577 程序员大数据hadoop人工智能
    做了那么多年开发，自学了很多门编程语言，我很明白学习资源对于学一门新语言的重要性，这些年也收藏了不少的Python干货，对我来说这些东西确实已经用不到了，但对于准备自学Python的人来说，或许它就是一个宝藏，可以给你省去很多的时间和精力。别在网上瞎学了，我最近也做了一些资源的更新，只要你是我的粉丝，这期福利你都可拿走。我先来介绍一下这些东西怎么用，文末抱走。（1）Python所有方向的学习路线（
  • 深度学习-13-小语言模型之SmolLM的使用 皮皮冰燃 深度学习深度学习
    文章附录1SmolLM概述1.1SmolLM简介1.2下载模型2运行2.1在CPU/GPU/多GPU上运行模型2.2使用torch.bfloat162.3通过位和字节的量化版本3应用示例4问题及解决4.1attention_mask和pad_token_id报错4.2max_new_tokens=205参考附录1SmolLM概述1.1SmolLM简介SmolLM是一系列尖端小型语言模型，提供三种规
  • 基于深度学习的农作物病害检测 SEU-WYL 深度学习dnn深度学习人工智能
    基于深度学习的农作物病害检测利用卷积神经网络（CNN）、生成对抗网络（GAN）、Transformer等深度学习技术，自动识别和分类农作物的病害，帮助农业工作者提高作物管理效率、减少损失。1.农作物病害检测的挑战病害种类繁多：农作物病害的类型多样，不同病害在同一作物上的表现差异很大，同时同一种病害在不同生长阶段的症状也可能不同。环境影响：天气、光照、湿度等外部环境因素会影响农作物的表现，使得病害检
  • 基于深度学习的文本引导的图像编辑 SEU-WYL 深度学习dnn深度学习人工智能
    基于深度学习的文本引导的图像编辑（Text-GuidedImageEditing）是一种通过自然语言文本指令对图像进行编辑或修改的技术。它结合了图像生成和自然语言处理（NLP）的最新进展，使用户能够通过描述性文本对图像内容进行精确的调整和操控。1.文本引导的图像编辑的挑战文本和图像之间的对齐：如何将文本中的语义信息准确地映射到图像中的特定区域或元素是一个关键挑战。这涉及到多模态数据的对齐和理解。编
  • 深度学习--对抗生成网络（GAN, Generative Adversarial Network） Ambition_LAO 深度学习生成对抗网络
    对抗生成网络（GAN,GenerativeAdversarialNetwork）是一种深度学习模型，由IanGoodfellow等人在2014年提出。GAN主要用于生成数据，通过两个神经网络相互对抗，来生成以假乱真的新数据。以下是对GAN的详细阐述，包括其概念、作用、核心要点、实现过程、代码实现和适用场景。1.概念GAN由两个神经网络组成：生成器（Generator）和判别器（Discrimina
  • 深度学习：怎么看pth文件的参数 奥利给少年 深度学习人工智能
    .pth文件是PyTorch模型的权重文件，它通常包含了训练好的模型的参数。要查看或使用这个文件，你可以按照以下步骤操作：1.确保你有模型的定义你需要有创建这个.pth文件时所用的模型的代码。这意味着你需要有模型的类定义和架构。2.加载模型权重使用PyTorch的load_state_dict方法来加载权重。这里是如何操作的：importtorchimporttorch.nnasnn#定义模型结构
  • chatgpt赋能python：如何在Python中安装Keras库？ turensu ChatGptpythonchatgptkeras计算机
    如何在Python中安装Keras库？Keras是一个简单易用的神经网络库，由FrançoisChollet编写。它在Python编程语言中实现了深度学习的功能，可以使您更轻松地构建和试验不同类型的神经网络。如果您是一名Python开发人员，肯定会想知道如何在您的Python项目中安装Keras库。在本文中，我们将向您展示如何安装和配置Keras库。步骤1：安装Python要使用Keras库，您需
  • 如何理解深度学习的训练过程 奋斗的草莓熊 深度学习人工智能pythonscikit-learnvirtualenvnumpypandas
    文章目录1.训练是干什么？2.预训练模型进行训练，主要更改的是预训练模型的什么东西？1.训练是干什么？以yolov5为例子，训练的目的是把一组输入猫狗图像放到神经网络中，得到一个输出模型，这个模型下次可以直接用来识别哪个是猫，哪个是狗2.预训练模型进行训练，主要更改的是预训练模型的什么东西？超参数（Hyperparameters）：这是模型结构中定义的参数，比如：卷积核大小（kernel_size
  • Keras深度学习框架入门及实战指南 司莹嫣Maude
    Keras深度学习框架入门及实战指南keraskeras-team/keras:是一个基于Python的深度学习库，它没有使用数据库。适合用于深度学习任务的开发和实现，特别是对于需要使用Python深度学习库的场景。特点是深度学习库、Python、无数据库。项目地址:https://gitcode.com/gh_mirrors/ke/keras一、项目介绍Keras简介Keras是一款高级神经网络
  • 深度学习驱动的车牌识别：技术演进与未来挑战 逼子歌 深度学习车牌识别神经网络字符识别YOLO卷积神经网络
    一、引言1.1研究背景在当今社会，智能交通系统的发展日益重要，而车牌识别作为其关键组成部分，发挥着至关重要的作用。车牌识别技术广泛应用于交通管理、停车场管理、安防监控等领域。在交通管理中，它可以用于车辆识别、交通违法监控和车流统计等，提高交通管理的效率和准确性。在停车场管理中，实现车辆的自动识别和收费，提升管理和服务水平。在安防监控领域，可用于追踪嫌疑人及犯罪行为。深度学习的出现为车牌识别带来了重
  • 每天五分钟玩转深度学习PyTorch：模型参数优化器torch.optim 幻风_huanfeng 深度学习框架pytorch深度学习pytorch人工智能神经网络机器学习优化算法
    本文重点在机器学习或者深度学习中，我们需要通过修改参数使得损失函数最小化(或最大化)，优化算法就是一种调整模型参数更新的策略。在pytorch中定义了优化器optim，我们可以使用它调用封装好的优化算法，然后传递给它神经网络模型参数，就可以对模型进行优化。本文是学习第6步(优化器)，参考链接pytorch的学习路线随机梯度下降算法在深度学习和机器学习中，梯度下降算法是最常用的参数更新方法，它的公式
  • 什么是AIGC？有哪些免费工具？ chent_某位 AIGC
    AIGC（AIGeneratedContent），即“人工智能生成内容”，是指通过人工智能技术自动生成各种类型的数字内容。AIGC让机器能够根据输入的信息或数据生成符合人类需求的文本、图像、音频、视频等内容，极大提高了内容创作的效率。AIGC的背景与起源随着深度学习和自然语言处理技术的快速发展，人工智能已经不再局限于简单的任务，如分类、预测和数据分析，而是具备了生成内容的能力。生成式AI模型，如O
  • transformer架构(Transformer Architecture)原理与代码实战案例讲解 AI架构设计之禅 大数据AI人工智能Python入门实战计算科学神经计算深度学习神经网络大数据人工智能大型语言模型AIAGILLMJavaPython架构设计AgentRPA
    transformer架构(TransformerArchitecture)原理与代码实战案例讲解关键词：Transformer,自注意力机制,编码器-解码器,预训练,微调,NLP,机器翻译作者：禅与计算机程序设计艺术/ZenandtheArtofComputerProgramming1.背景介绍1.1问题的由来自然语言处理（NLP）领域的发展经历了从规则驱动到统计驱动再到深度学习驱动的三个阶段。
  • 如何有效的学习AI大模型？ Python程序员罗宾 学习人工智能语言模型自然语言处理架构
    学习AI大模型是一个系统性的过程，涉及到多个学科的知识。以下是一些建议，帮助你更有效地学习AI大模型：基础知识储备：数学基础：学习线性代数、概率论、统计学和微积分等，这些是理解机器学习算法的数学基础。编程技能：掌握至少一种编程语言，如Python，因为大多数AI模型都是用Python实现的。理论学习：机器学习基础：了解监督学习、非监督学习、强化学习等基本概念。深度学习：学习神经网络的基本结构，如卷
  • 【深度学习】【OnnxRuntime】【Python】模型转化、环境搭建以及模型部署的详细教程 牙牙要健康 深度学习onnxonnxruntime深度学习python人工智能
    【深度学习】【OnnxRuntime】【Python】模型转化、环境搭建以及模型部署的详细教程提示:博主取舍了很多大佬的博文并亲测有效,分享笔记邀大家共同学习讨论文章目录【深度学习】【OnnxRuntime】【Python】模型转化、环境搭建以及模型部署的详细教程前言模型转换--pytorch转onnxWindows平台搭建依赖环境onnxruntime调用onnx模型ONNXRuntime推理核
  • java的(PO,VO,TO,BO,DAO,POJO) Cb123456 VOTOBOPOJODAO
    转: http://www.cnblogs.com/yxnchinahlj/archive/2012/02/24/2366110.html   -------------------------------------------------------------------  O/R Mapping 是 Object Relational Mapping（对象关系映
  • spring ioc原理（看完后大家可以自己写一个spring） aijuans spring
             最近，买了本Spring入门书：spring In Action 。大致浏览了下感觉还不错。就是入门了点。Manning的书还是不错的，我虽然不像哪些只看Manning书的人那样专注于Manning,但怀着崇敬 的心情和激情通览了一遍。又一次接受了IOC 、DI、AOP等Spring核心概念。 先就IOC和DI谈一点我的看法。IO
  • MyEclipse 2014中Customize Persperctive设置无效的解决方法 Kai_Ge MyEclipse2014
    高高兴兴下载个MyEclipse2014，发现工具条上多了个手机开发的按钮，心生不爽就想弄掉他！ 结果发现Customize Persperctive失效！！ 有说更新下就好了，可是国内Myeclipse访问不了，何谈更新... so~这里提供了更新后的一下jar包，给大家使用！ 1、将9个jar复制到myeclipse安装目录\plugins中 2、删除和这9个jar同包名但是版本号较
  • SpringMvc上传 120153216 springMVC
      @RequestMapping(value = WebUrlConstant.UPLOADFILE) @ResponseBody public Map<String, Object> uploadFile(HttpServletRequest request,HttpServletResponse httpresponse) { try { //
  • Javascript----HTML DOM 事件 何必如此 JavaScripthtmlWeb
    HTML DOM 事件允许Javascript在HTML文档元素中注册不同事件处理程序。 事件通常与函数结合使用，函数不会在事件发生前被执行！ 注：DOM： 指明使用的 DOM 属性级别。 1.鼠标事件 属性               
  • 动态绑定和删除onclick事件 357029540 JavaScriptjquery
    因为对JQUERY和JS的动态绑定事件的不熟悉，今天花了好久的时间才把动态绑定和删除onclick事件搞定!现在分享下我的过程。      在我的查询页面，我将我的onclick事件绑定到了tr标签上同时传入当前行(this值)参数，这样可以在点击行上的任意地方时可以选中checkbox，但是在我的某一列上也有一个onclick事件是用于下载附件的，当
  • HttpClient|HttpClient请求详解 7454103 apache应用服务器网络协议网络应用Security
    HttpClient 是 Apache Jakarta Common 下的子项目，可以用来提供高效的、最新的、功能丰富的支持 HTTP 协议的客户端编程工具包，并且它支持 HTTP 协议最新的版本和建议。本文首先介绍 HTTPClient，然后根据作者实际工作经验给出了一些常见问题的解决方法。HTTP 协议可能是现在 Internet 上使用得最多、最重要的协议了，越来越多的 Java 应用程序需
  • 递归 逐层统计树形结构数据 darkranger 数据结构
    将集合递归获取树形结构: /** * * 递归获取数据 * @param alist:所有分类 * @param subjname:对应统计的项目名称 * @param pk:对应项目主键 * @param reportList: 最后统计的结果集 * @param count:项目级别 */ public void getReportVO(Arr
  • 访问WEB-INF下使用frameset标签页面出错的原因 aijuans struts2
    <frameset rows="61,*,24" cols="*" framespacing="0" frameborder="no" border="0">        
  • MAVEN常用命令 avords
    Maven库： http://repo2.maven.org/maven2/ Maven依赖查询： http://mvnrepository.com/ Maven常用命令： 1. 创建Maven的普通java项目：    mvn archetype:create    -DgroupId=packageName 
  • PHP如果自带一个小型的web服务器就好了 houxinyou apache应用服务器WebPHP脚本
    最近单位用PHP做网站，感觉PHP挺好的，不过有一些地方不太习惯，比如，环境搭建。PHP本身就是一个网站后台脚本，但用PHP做程序时还要下载apache，配置起来也不太很方便，虽然有好多配置好的apache+php+mysq的环境，但用起来总是心里不太舒服，因为我要的只是一个开发环境，如果是真实的运行环境，下个apahe也无所谓，但只是一个开发环境，总有一种杀鸡用牛刀的感觉。如果php自己的程序中
  • NoSQL数据库之Redis数据库管理(list类型) bijian1013 redis数据库NoSQL
    3.list类型及操作         List是一个链表结构，主要功能是push、pop、获取一个范围的所有值等等，操作key理解为链表的名字。Redis的list类型其实就是一个每个子元素都是string类型的双向链表。我们可以通过push、pop操作从链表的头部或者尾部添加删除元素，这样list既可以作为栈，又可以作为队列。   &nbs
  • 谁在用Hadoop？ bingyingao hadoop数据挖掘公司应用场景
    Hadoop技术的应用已经十分广泛了，而我是最近才开始对它有所了解，它在大数据领域的出色表现也让我产生了兴趣。浏览了他的官网，其中有一个页面专门介绍目前世界上有哪些公司在用Hadoop，这些公司涵盖各行各业，不乏一些大公司如alibaba,ebay,amazon,google,facebook,adobe等，主要用于日志分析、数据挖掘、机器学习、构建索引、业务报表等场景,这更加激发了学习它的热情。
  • 【Spark七十六】Spark计算结果存到MySQL bit1129 mysql
    package spark.examples.db import java.sql.{PreparedStatement, Connection, DriverManager} import com.mysql.jdbc.Driver import org.apache.spark.{SparkContext, SparkConf} object SparkMySQLInteg
  • Scala: JVM上的函数编程 bookjovi scalaerlanghaskell
        说Scala是JVM上的函数编程一点也不为过，Scala把面向对象和函数型编程这两种主流编程范式结合了起来，对于熟悉各种编程范式的人而言Scala并没有带来太多革新的编程思想，scala主要的有点在于Java庞大的package优势，这样也就弥补了JVM平台上函数型编程的缺失，MS家.net上已经有了F#，JVM怎么能不跟上呢？     对本人而言
  • jar打成exe bro_feng java jar exe
    今天要把jar包打成exe，jsmooth和exe4j都用了。 遇见几个问题。记录一下。 两个软件都很好使，网上都有图片教程，都挺不错。 首先肯定是要用自己的jre的，不然不能通用，其次别忘了把需要的lib放到classPath中。 困扰我很久的一个问题是，我自己打包成功后，在一个同事的没有装jdk的电脑上运行，就是不行，报错jvm.dll为无效的windows映像，如截图 最后发现
  • 读《研磨设计模式》-代码笔记-策略模式-Strategy bylijinnan java设计模式
    声明： 本文只为方便我个人查阅和理解，详细的分析以及源代码请移步 原作者的博客http://chjavach.iteye.com/ /* 策略模式定义了一系列的算法，并将每一个算法封装起来，而且使它们还可以相互替换。策略模式让算法独立于使用它的客户而独立变化 简单理解： 1、将不同的策略提炼出一个共同接口。这是容易的，因为不同的策略，只是算法不同，需要传递的参数
  • cmd命令值cvfM命令 chenyu19891124 cmd
         cmd命令还真是强大啊。今天发现jar -cvfM aa.rar @aaalist 就这行命令可以根据aaalist取出相应的文件   例如：      在d：\workspace\prpall\test.java 有这样一个文件，现在想要将这个文件打成一个包。运行如下命令即可比如在d：\wor
  • OpenJWeb(1.8) Java Web应用快速开发平台 comsci java框架Web项目管理企业应用
        OpenJWeb(1.8) Java Web应用快速开发平台的作者是我们技术联盟的成员，他最近推出了新版本的快速应用开发平台  OpenJWeb(1.8)，我帮他做做宣传   OpenJWeb快速开发平台以快速开发为核心，整合先进的java 开源框架，本着自主开发+应用集成相结合的原则，旨在为政府、企事业单位、软件公司等平台用户提供一个架构透
  • Python 报错：IndentationError: unexpected indent daizj pythontab空格缩进
        IndentationError: unexpected indent 是缩进的问题，也有可能是tab和空格混用啦     Python开发者有意让违反了缩进规则的程序不能通过编译，以此来强制程序员养成良好的编程习惯。并且在Python语言里，缩进而非花括号或者某种关键字，被用于表示语句块的开始和退出。增加缩进表示语句块的开
  • HttpClient 超时设置 dongwei_6688 httpclient
    HttpClient中的超时设置包含两个部分： 1. 建立连接超时，是指在httpclient客户端和服务器端建立连接过程中允许的最大等待时间 2. 读取数据超时，是指在建立连接后，等待读取服务器端的响应数据时允许的最大等待时间   在HttpClient 4.x中如下设置：   HttpClient httpclient = new DefaultHttpC
  • 小鱼与波浪 dcj3sjt126com
    一条小鱼游出水面看蓝天，偶然间遇到了波浪。　　小鱼便与波浪在海面上游戏，随着波浪上下起伏、汹涌前进。　　小鱼在波浪里兴奋得大叫：“你每天都过着这么刺激的生活吗？简直太棒了。”　　波浪说：“岂只每天过这样的生活，几乎每一刻都这么刺激！还有更刺激的，要有潮汐变化，或者狂风暴雨，那才是兴奋得心脏都会跳出来。”　　小鱼说：“真希望我也能变成一个波浪，每天随着风雨、潮汐流动，不知道有多么好！”　　很快，小鱼
  • Error Code: 1175 You are using safe update mode and you tried to update a table dcj3sjt126com mysql
    快速高效用：SET SQL_SAFE_UPDATES = 0；下面的就不要看了！ 今日用MySQL Workbench进行数据库的管理更新时，执行一个更新的语句碰到以下错误提示： Error Code: 1175 You are using safe update mode and you tried to update a table without a WHERE that
  • 枚举类型详细介绍及方法定义 gaomysion enumjavaee
    转发 http://developer.51cto.com/art/201107/275031.htm 枚举其实就是一种类型，跟int, char 这种差不多，就是定义变量时限制输入的，你只能够赋enum里面规定的值。建议大家可以看看，这两篇文章，《java枚举类型入门》和《C++的中的结构体和枚举》，供大家参考。 枚举类型是JDK5.0的新特征。Sun引进了一个全新的关键字enum
  • Merge Sorted Array hcx2013 array
    Given two sorted integer arrays nums1 and nums2, merge nums2 into nums1 as one sorted array. Note:You may assume that nums1 has enough space (size that is
  • Expression Language 3.0新特性 jinnianshilongnian el 3.0
    Expression Language 3.0表达式语言规范最终版从2013-4-29发布到现在已经非常久的时间了；目前如Tomcat 8、Jetty 9、GlasshFish 4已经支持EL 3.0。新特性包括：如字符串拼接操作符、赋值、分号操作符、对象方法调用、Lambda表达式、静态字段/方法调用、构造器调用、Java8集合操作。目前Glassfish 4/Jetty实现最好，对大多数新特性
  • 超越算法来看待个性化推荐 liyonghui160com 超越算法来看待个性化推荐
             一提到个性化推荐，大家一般会想到协同过滤、文本相似等推荐算法，或是更高阶的模型推荐算法，百度的张栋说过，推荐40%取决于UI、30%取决于数据、20%取决于背景知识，虽然本人不是很认同这种比例，但推荐系统中，推荐算法起的作用起的作用是非常有限的。       就像任何
  • 写给Javascript初学者的小小建议 pda158 JavaScript
    　　一般初学JavaScript的时候最头痛的就是浏览器兼容问题。在Firefox下面好好的代码放到IE就不能显示了，又或者是在IE能正常显示的代码在firefox又报错了。 　　如果你正初学JavaScript并有着一样的处境的话建议你：初学JavaScript的时候无视DOM和BOM的兼容性，将更多的时间花在 了解语言本身（ECMAScript）。只在特定浏览器编写代码（Chrome/Fi
  • Java 枚举 ShihLei javaenum枚举
    注：文章内容大量借鉴使用网上的资料，可惜没有记录参考地址，只能再传对作者说声抱歉并表示感谢！   一 基础 1）语法      枚举类型只能有私有构造器（这样做可以保证客户代码没有办法新建一个enum的实例）      枚举实例必须最先定义 2）特性     &nb
  • Java SE 6 HotSpot虚拟机的垃圾回收机制 uuhorse javaHotSpotGC垃圾回收VM
    官方资料，关于Java SE 6 HotSpot虚拟机的garbage Collection，非常全，英文。 http://www.oracle.com/technetwork/java/javase/gc-tuning-6-140523.html   Java SE 6 HotSpot[tm] Virtual Machine Garbage Collection Tuning &
按字母分类： ABCDEFGHIJKLMNOPQRSTUVWXYZ其他