位图与布隆过滤器

位图

位图就是stl里面的bitset。一个位可以记录两个状态。适用于海量数据，数据无重复的场景。通常是用来判断某个数据存不存在的。

bitset的使用

bitset的[]和set,reset都是很好用的接口。

1. []可以让你快速在某一位中插入一个数字。
2. set可以让你在指定位置中变成1
3. reset可以让你在指定位置中变成0
4. bitset的构造函数要传字符串

int main()
{
	bitset<16> foo("0000000000000000");
	foo[1] = 1;
	foo[10] = 1;
	foo.set(11, 1);
	foo.reset(10);
	cout << foo << endl;
}

自己实现bitset

代码也很简单，就是位运算而已。

关于这个模板参数size_t N,这个是非类型的模板参数。每次都可以指定开辟的空间大小，单位是bit。

也就是说bitset<10>的意思就是有10个比特位的位图。

template<size_t N>
class bitset
{
public:
	bitset()
	{
		table.resize(N / 32 + 1, 0);
	}

	void set(size_t pos)
	{
		int i = pos / N;//第i个int
		int j = pos % N;//第i个int的第j个位置
		table[i] |= (1 << j - 1);
	}

	void reset(size_t pos)
	{
		int i = pos / N;
		int j = pos % N;
		table[i] &= (~(1 << (j - 1)));
	}

	bool test(size_t pos)
	{
		int i = pos / N;
		int j = pos % N;
		return table[i] & (1 << j - 1);
	}
private:
	vector<int> table;
};

ps:让某一位变成1或者0，不要再写成让该数字右移了。要让1左移x位然后进行运算。

位图的应用

首先要记住下面两个换算：
1.1G = 10亿字节
2.1G = 2^30

1.给定100亿个整数（int)，设计算法找到只出现一次的整数？

100亿个int,如果用哈希表存的话，就要40G的内存。
(1G = 10亿字节，100亿个int = 400亿字节 = 40G）
很浪费空间，不行。

因此就用位图来存。由于100亿个int里面肯定有有重复的数据（int最多表示42亿个数字）。因此用42亿多的比特位来存储每个数字是否出现过即可。

42亿多比特大概是5亿多字节，也就是512M，大大节省了空间。

至于怎么找到只出现过一次的整数。我们用两张位图就可以解决了。

举个例子：
此时拿到一个新数字。看两张位图，发现是10，就把10改成1即可。证明这个数字已经出现三次了。

---

2.给两个文件，分别有100亿个整数（int)，我们只有1G内存，如何找到两个文件交集？

用一个位图存这100亿个整数的状态，然后再去第二个文件里面读取数据，如果这个数据在位图里面出现过，就是交集。这样是可以的，但是IO次数可能稍微多了点。

最好用两个位图存起来，如果两个位图的标识都是1，代表是交集。
上面我们算过了，一个位图是512M，两个位图刚好1G

---

3.位图应用变形：1个文件有100亿个int，1G内存，设计算法找到出现次数不超过2次的所有整数

和第一题一模一样。

布隆过滤器

上面说的位图其实就是直接定址法的哈希。
布隆过滤器是经过哈希函数处理后的位图。

给一个情景：在一个用户注册账号，如何快速判断这个电话号码是已经注册过的？

当然，我们可以直接去数据库查找，但是由于数据库在磁盘上，需要IO。这无法满足快速的要求。

因此就需要用到布隆过滤器。先把这个字符串在布隆过滤器的位图上看一下，这个电话号码的字符串是否已经注册过了，如果布隆过滤器说已经注册过了，那就去后台的数据库再查看一下（布隆过滤器有可能会冲突，不能保证数据一定存在）。如果布隆过滤器说没有注册过，那么它一定没有注册过。

布隆过滤器原理及实现

基于上面的场景，对于字符串我们也要进行哈希成整型值。对于布隆过滤器来讲，为了减少冲突的可能性，一个字符串我们采用多种（可以是3，4，5甚至更多）哈希算法来得到不同的哈希值。并在位图上都标注成1.

当属于该字符串的哈希值都相同时，才认为二者相同。

举个例子：

总结一下就是：对一个字符串采用不同的哈希函数映射成整型，然后放到位图里面。这就叫布隆过滤器。

布隆过滤器不能保证冲突的字符串一定是相同的。这很好理解，和之前哈希一样。这也是为什么这时候要去数据库再次验证的原因。
布隆过滤器可以保证不冲突的字符串一定是不同的。这点和哈希也一样。

实现：
各种字符串哈希算法实现
在上面的文章里面随便选几个字符串哈希算法来进行映射。

#include 
#include 
using namespace std;

struct hashBKDR
{
	size_t operator()(const string& s)
	{
		size_t val = 0;
		for (auto& e : s)
		{
			val *= 131;
			val += e;
		}
		return val;
	}
};


struct hashSDBM
{
	size_t operator()(const string& s)
	{
		const char* str = s.c_str();
		register size_t hash = 0;
		while (size_t ch = (size_t)*str++)
		{
			hash = 65599 * hash + ch;
		}
		return hash;
	}
};

struct hashRS
{
	size_t operator()(const string& s)
	{
		const char* str = s.c_str();
		register size_t hash = 0;
		size_t magic = 63689;
		while (size_t ch = (size_t)*str++)
		{
			hash = hash * magic + ch;
			magic *= 378551;
		}
		return hash;
	}
};

template<size_t N, class hash1 = hashBKDR, class hash2 = hashSDBM, class hash3 = hashRS>
class bloomfilter
{
public:
	void insert(const string& s)
	{
		int i = hash1()(s) % N, j = hash2()(s) % N, k = hash3()(s) % N;
		table[i] = 1, table[j] = 1, table[k] = 1;
	}

	bool isInBloomFilter(const string& s)
	{
		int i = hash1()(s) % N, j = hash2()(s) % N, k = hash3()(s) % N;
		if (table[i] == 1 && table[j] == 1 && table[k] == 1) return true;
		else return false;
	}
private:
	bitset<N> table;
};

int main()
{
	bloomfilter<100> bf;
	
	bf.insert("https://www.acwing.com/activity/content/code/content/45308/");
	bf.insert("https://leetcode-cn.com/problems/intersection-of-two-arrays/");
	cout << bf.isInBloomFilter("https://leetcode-cn.com/problems/intersection-of-two-arrays/") << endl;
	cout << bf.isInBloomFilter("https://leetcode-cn.com/problems/intersection-of-two-arrays/1") << endl;

}

总结一下：
关于布隆过滤器最重要的两点：

1. 冲突的数据不一定已经在布隆过滤器存在（专业术语叫误判），因此要再次验证。不冲突的数据一定不存在于布隆过滤器。
2. 布隆过滤器就是对一个数据采用不同哈希策略的位图

布隆过滤器的删除

我们不能直接对布隆过滤器进行删除。
下面这张图：
如果我们直接把李四删除，那么关于张三的哈希值也被误删了。那么张三也没有了。

位图的基本单位是比特，因此布隆过滤器不支持删除。但是如果位图的基本单位是char或者更多字节，就支持删除了。（kv模型）

如下图：删除李四的时候，把节点的值-1即可。（kv模型）

布隆过滤器的题目

给两个文件，分别有100亿个query，我们只有1G内存，如何找到两个文件交集？分别给出精确算法和近似算法

query就是字符串。
对于近似算法：我们把一个文件里面的query全部存在布隆过滤器里面。然后从第二个文件里面读取query，看一下它是否在布隆过滤器里面。由于布隆过滤器会出现误判现象，因此这是近似算法。

对于精确算法：我们需要采用哈希切割。
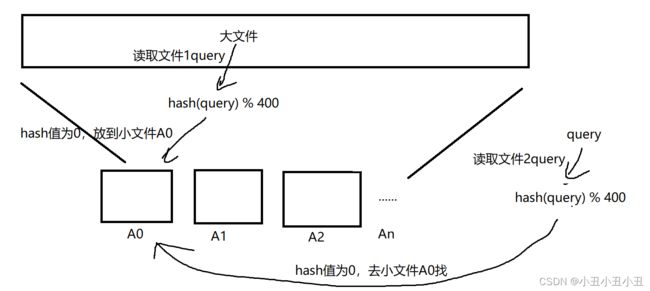
把第一个文件切分成若干个小文件（切分不是平均分，说是切分，其实是创建400个文件，然后从大文件里面剪切数据到文件里面，因为每个数据的hash值不确定，因此这400个文件的大小也是不确定的）。
然后从文件1里面读取每一条query，存放在下标为hash(query) % 400的文件。对于文件2，直接读取query，对它进行hash。然后去对应的hash值的小文件里面找是否有这个query，有就是交集，没有就不是。

哈希切割

哈希切割步骤：
1.根据给的内存大小创建N个文件
2.将数据经过hash之后剪切对应的小文件里面
3.如果小文件变大了就继续哈希切割。
4.放完之后统计相应信息

给一个超过100G大小的log file, log中存着IP地址, 设计算法找到出现次数最多的IP地址？ 与上题条件相同，如何找到top K的IP？

先创建N个文件，然后把每条数据都hash之后剪切到对应的小文件里。由于ip地址可以用inet_addr把字符串的ip转换成整型。因此可以直接hash映射。

把所有ip地址都放进小文件里面。建立map来统计所有ip地址出现的次数。遍历完之后就能找到出现次数最多的ip地址了。

如果要找出现top K的ip地址，建立大小为k的小堆。堆里面放pair，遇到次数比堆顶大的ip地址，就把堆顶pop，并插入新的ip地址。最后堆里面就是出现最多的K个ip地址。