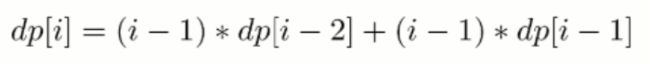leetcode | 分类整理4(动态规划)
递归和动态规划都是将原问题拆成多个子问题然后求解,他们之间最本质的区别是,动态规划保存了子问题的解,避免重复计算。
重点都是要找到转移方程
Fibonacci:
在上述方法中,我们使用 dp 数组,其中 dp[i]=dp[i-1]+dp[i-2]。可以很容易通过分析得出 dp[i]其实就是第 ii个斐波那契数。
Fib(n)=Fib(n−1)+Fib(n−2)
重点是确定pre1和pre2,以及最后要返回哪个
70. 爬楼梯(e)
198. 打家劫舍(e)
dp[i] = max(dp[i-2]+num[i], dp[i-1])
213. 打家劫舍2(m)
强盗在环形区抢劫
环状排列意味着第一个房子和最后一个房子中只能选择一个偷窃,因此可以把此环状排列房间问题约化为两个单排排列房间子问题:
在不偷窃第一个房子的情况下(即nums[1:]),最大金额是 p_1
在不偷窃最后一个房子的情况下(即 nums[:n−1]),最大金额是 p_2
综合偷窃最大金额: 为以上两种情况的较大值,即 max(p1,p2)。
public int rob(int[] nums) {
if (nums == null || nums.length <= 0) {
return 0;
}
if (nums.length == 1) {
return nums[0];
}
int n = nums.length;
return Math.max(robHelper(nums,0,n-1),robHelper(nums,1,n));
}
private int robHelper(int[] nums, int start, int end) {
int pre2 = 0 , pre1 = nums[start];
for (int i = start + 1; i < end; i++) {
int cur = Math.max(pre2+nums[i],pre1);
pre2 = pre1;
pre1 = cur;
}
return pre1;
}
4. 信件错排
题目描述:有 N 个 信 和 信封,它们被打乱,求错误装信方式的数量。
定义一个数组 dp 存储错误方式数量,dp[i] 表示前 i 个信和信封的错误方式数量。假设第 i 个信装到第 j 个信封里面,而第 j 个信装到第 k 个信封里面。根据 i 和 k 是否相等,有两种情况:
- i==k,交换 i 和 j 的信后,它们的信和信封在正确的位置,但是其余 i-2 封信有 dp[i-2] 种错误装信的方式。由于 j 有 i-1 种取值,因此共有 (i-1)*dp[i-2] 种错误装信方式。
- i != k,交换 i 和 j 的信后,第 i 个信和信封在正确的位置,其余 i-1 封信有 dp[i-1] 种错误装信方式。由于 j 有 i-1 种取值,因此共有 (i-1)*dp[i-1] 种错误装信方式。
综上所述,错误装信数量方式数量为:
矩阵路径:
64. 最小路径和(m)
重点:一维动态规划,dp 数组的大小和行大小相同。这是因为对于某个固定状态,只需要考虑下方和右侧的节点。
题目要求,只能向右或向下走,换句话说,当前单元格 (i,j)只能从左方单元格 (i−1,j) 或上方单元格 (i,j−1) 走到,因此只需要考虑矩阵左边界和上边界。
public int minPathSum(int[][] grid) {
if (grid.length == 0 || grid[0].length == 0) {
return 0;
}
int m = grid.length, n = grid[0].length;
int[] dp = new int[n];
for (int i = 0 ;i < m; i++) {
for (int j = 0 ;j < n;j ++) {
if (i == 0 && j == 0) {
dp[j] = grid[i][j];
}
// 第一行,只能从左边来
else if (i == 0) {
dp[j] = dp[j-1] + grid[i][j];
}
// 第一列,只能从上边来
else if (j == 0) {
dp[j] = dp[j] + grid[i][j];
}
else {
dp[j] = Math.min(dp[j],dp[j-1])+grid[i][j];
}
}
}
return dp[n-1];
}
62. 不同路径(m)
从左边来的dp[i-1][j]+从上边来的dp[i][j-1]
public int uniquePaths(int m, int n) {
int[][] dp = new int[m][n];
for (int i = 0; i < n; i++) dp[0][i] = 1;
for (int i = 0; i < m; i++) dp[i][0] = 1;
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
}
return dp[m - 1][n - 1];
}使用二维数组的时候,dp[i][j] = dp[i-1][j] + dp[i][j-1] ,每一个格子的数据等于上面一个格子加左边格子的数据。可以想象一下,计算一行数据的时候,直接把上面一行的数据搬下来,然后每个格子就等于前一个格子的数据加上当前格子的数据。
public int uniquePaths(int m, int n) {
int[] cur = new int[n];
Arrays.fill(cur,1);
for (int i = 1; i < m;i++){
for (int j = 1; j < n; j++){
cur[j] += cur[j-1] ;
}
}
return cur[n-1];
}
数组区间:
303. 区域和检索(e)
private int[] sum;
public _303sumOfArray_e(int[] nums) {
sum = new int[nums.length+1];
for (int i = 0; i < nums.length; i++) {
sum[i+1] = sum[i] + nums[i];
}
}
public int sumRange(int i, int j) {
return sum[j+1] - sum[i];
}
413. 等差数列划分(m)
dp[i] 表示以 A[i] 为结尾的等差递增子区间的个数。
当 A[i] - A[i-1] == A[i-1] - A[i-2],那么 [A[i-2], A[i-1], A[i]] 构成一个等差递增子区间。而且在以 A[i-1] 为结尾的递增子区间的后面再加上一个 A[i],一样可以构成新的递增子区间。
dp[2] = 1
[0, 1, 2]
dp[3] = dp[2] + 1 = 2
[0, 1, 2, 3], // [0, 1, 2] 之后加一个 3
[1, 2, 3] // 新的递增子区间
dp[4] = dp[3] + 1 = 3
[0, 1, 2, 3, 4], // [0, 1, 2, 3] 之后加一个 4
[1, 2, 3, 4], // [1, 2, 3] 之后加一个 4
[2, 3, 4] // 新的递增子区间综上,在 A[i] - A[i-1] == A[i-1] - A[i-2] 时,dp[i] = dp[i-1] + 1。
public int numberOfArithmeticSlices(int[] A) {
if (A == null || A.length <= 0) {
return 0;
}
int n = A.length;
// dp[i]是以A[i]结尾的子区间的个数
int[] dp = new int[n];
for (int i = 2; i < n; i++) {
if (A[i]-A[i-1] == A[i-1]-A[i-2]) {
dp[i] = dp[i-1] + 1;
}
}
int total = 0;
for (int i = 2; i < n; i++) {
total += dp[i];
}
return total;
}
子序列:
300. 最长递增子序列(m)
已知一个序列 {S1, S2,...,Sn},取出若干数组成新的序列 {Si1, Si2,..., Sim},其中 i1、i2 ... im 保持递增,即新序列中各个数仍然保持原数列中的先后顺序,称新序列为原序列的一个 子序列 。
如果在子序列中,当下标 ix > iy 时,Six > Siy,称子序列为原序列的一个 递增子序列 。
定义一个数组 dp 存储最长递增子序列的长度,dp[n] 表示以 Sn 结尾的序列的最长递增子序列长度。对于一个递增子序列 {Si1, Si2,...,Sim},如果 im < n 并且 Sim < Sn,此时 {Si1, Si2,..., Sim, Sn} 为一个递增子序列,递增子序列的长度增加 1。满足上述条件的递增子序列中,长度最长的那个递增子序列就是要找的,在长度最长的递增子序列上加上 Sn 就构成了以 Sn 为结尾的最长递增子序列。因此 dp[n] = max{ dp[i]+1 | Si < Sn && i < n} 。
重点:二分查找
定义一个 tails 数组,其中 tails[i] 存储长度为 i + 1 的最长递增子序列的最后一个元素。对于一个元素 x,
- 如果它大于 tails 数组所有的值,那么把它添加到 tails 后面,表示最长递增子序列长度加 1;
- 如果 tails[i-1] < x <= tails[i],那么更新 tails[i] = x。
例如对于数组 [4,3,6,5],有:
tails len num
[] 0 4
[4] 1 3
[3] 1 6
[3,6] 2 5
[3,5] 2 null可以看出 tails 数组保持有序,因此在查找 Si 位于 tails 数组的位置时就可以使用二分查找。
public int lengthOfLIS(int[] nums) {
int n = nums.length;
int[] tails = new int[n];
int len = 0;
for (int num : nums) {
int index = binarySearch(tails,len,num);
tails[index] = num;
if (index == len) {
len++;
}
}
return len;
}
private int binarySearch(int[] tails,int len, int key) {
int l = 0, r = len;
while (l < r) {
int mid = l + (r-l)/2;
if (tails[mid] == key) {
return mid;
}
else if (tails[mid] < key) {
l = mid + 1;
}
else {
r = mid;
}
}
return l;
}
1143. 最长公共子序列(m)
动规流程:
第一步,一定要明确 dp 数组的含义。
dp[i][j] 的含义是:对于 s1[1..i] 和 s2[1..j],它们的 LCS 长度是 dp[i][j]。
第二步,定义 base case。
我们专门让索引为 0 的行和列表示空串,dp[0][..] 和 dp[..][0] 都应该初始化为 0,这就是 base case。
第三步,找状态转移方程。
用两个指针 i 和 j 从前往后遍历 s1 和 s2,如果 s1[i]==s2[j],那么这个字符一定在 lcs 中;否则的话,s1[i] 和 s2[j] 这两个字符至少有一个不在 lcs 中,需要丢弃一个(留下的是max(dp[i-1][j], dp[i],[j-1]))。
public int longestCommonSubsequence(String text1, String text2) {
int len1 = text1.length(), len2 = text2.length();
int[][] dp = new int[len1+1][len2+1];
for (int i = 1; i <= len1; i++) {
for (int j = 1; j <= len2; j++) {
if (text1.charAt(i-1) == text2.charAt(j-1) ) {
dp[i][j] = dp[i-1][j-1] + 1;
}
else {
dp[i][j] = Math.max(dp[i-1][j],dp[i][j-1]);
}
}
}
return dp[len1][len2];
}