力扣刷题笔记23—— 二叉树中和为某一值的路径/DFS和BFS/push_back和emplace_back的差异/移动构造函数

问题

来自力扣：

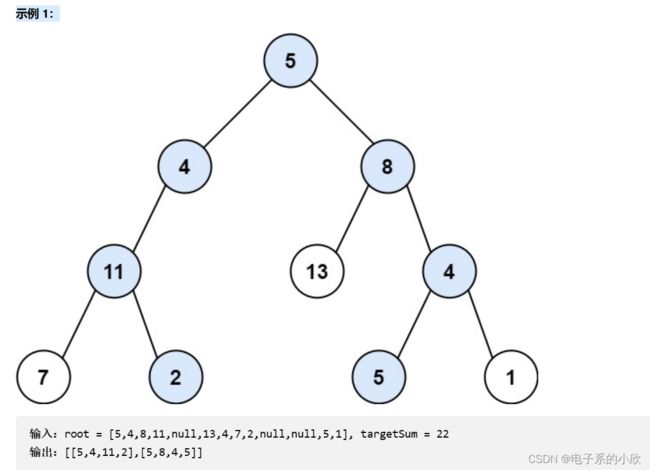
给你二叉树的根节点 root 和一个整数目标和 targetSum ，找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。

叶子节点 是指没有子节点的节点。

示例代码

最近的状态：简单的题不想记笔记，繁琐的题不想自己码代码。
这其实就是一个遍历的代码，遍历所有节点。

方法一深度优先搜索

采用深度优先搜索的方式，枚举每一条从根节点到叶子节点的路径。当我们遍历到叶子节点，且此时路径和恰为目标和时，我们就找到了一条满足条件的路径。

class Solution {
public:
    vector<vector<int>> ret;
    vector<int> path;

    void dfs(TreeNode* root, int target) {
        if (root == nullptr) {
            return;
        }
        path.emplace_back(root->val);
        target -= root->val;
        if (root->left == nullptr && root->right == nullptr && target == 0) {
            ret.emplace_back(path);
        }
        dfs(root->left, target);
        dfs(root->right, target);
        path.pop_back();
    }

    vector<vector<int>> pathSum(TreeNode* root, int target) {
        dfs(root, target);
        return ret;
    }
};

方法二广度优先搜索

采用广度优先搜索的方式，遍历这棵树。当我们遍历到叶子节点，且此时路径和恰为目标和时，我们就找到了一条满足条件的路径.

class Solution {
public:
    vector<vector<int>> ret;
    unordered_map<TreeNode*, TreeNode*> parent;

    void getPath(TreeNode* node) {
        vector<int> tmp;
        while (node != nullptr) {
            tmp.emplace_back(node->val);
            node = parent[node];
        }
        reverse(tmp.begin(), tmp.end());
        ret.emplace_back(tmp);
    }

    vector<vector<int>> pathSum(TreeNode* root, int target) {
        if (root == nullptr) {
            return ret;
        }

        queue<TreeNode*> que_node;
        queue<int> que_sum;
        que_node.emplace(root);
        que_sum.emplace(0);

        while (!que_node.empty()) {
            TreeNode* node = que_node.front();
            que_node.pop();
            int rec = que_sum.front() + node->val;
            que_sum.pop();

            if (node->left == nullptr && node->right == nullptr) {
                if (rec == target) {
                    getPath(node);
                }
            } else {
                if (node->left != nullptr) {
                    parent[node->left] = node;
                    que_node.emplace(node->left);
                    que_sum.emplace(rec);
                }
                if (node->right != nullptr) {
                    parent[node->right] = node;
                    que_node.emplace(node->right);
                    que_sum.emplace(rec);
                }
            }
        }

        return ret;
    }
};

关于广度优先和深度优先搜索的原理，可以看看我的另一个专栏。人工智能算法中的盲目搜索

push_back和emplace_back

参考文章
这两个的功能都是向vector容器的尾部添加元素。区别是前者需要先创建，然后再拷贝进vector。后者则是直接在vector的尾部创建元素。所以emplace_back的执行效率更高，但它是C++11标准新加的，所以如果考虑兼容性，就得用push_back。
代码：

#include  
#include  
using namespace std;
class testDemo
{
public:
    testDemo(int num):num(num){
        std::cout << "调用构造函数" << endl;
    }
    testDemo(const testDemo& other) :num(other.num) {
        std::cout << "调用拷贝构造函数" << endl;
    }
    testDemo(testDemo&& other) :num(other.num) {
        std::cout << "调用移动构造函数" << endl;
    }
private:
    int num;
};

int main()
{
    cout << "emplace_back:" << endl;
    std::vector<testDemo> demo1;
    demo1.emplace_back(2);  

    cout << "push_back:" << endl;
    std::vector<testDemo> demo2;
    demo2.push_back(2);
}

结果：

emplace_back:
调用构造函数
push_back:
调用构造函数
调用移动构造函数

移动构造函数

参考文章
在上面的代码中，出现了移动构造函数。印象中没学过，所以也查了下。

当我们利用拷贝构造函数进行深拷贝时，实际上会多出一次深拷贝操作，因为需要想创建一个，然后拷贝过来，在销毁那个用来拷贝的。为了提高效率，C++11就多了移动构造函数。当进行深拷贝时，不会再去让新指针指向新的空间，而是将新指针指向临时指针的空间，然后把临时指针指向NULL。这样就减少了一次拷贝。
这个是参考文章里的代码：

#include 
using namespace std;
class demo{
public:
    demo():num(new int(0)){
        cout<<"construct!"<<endl;
    }

    demo(const demo &d):num(new int(*d.num)){
        cout<<"copy construct!"<<endl;
    }
    //添加移动构造函数
    demo(demo &&d):num(d.num){
        d.num = NULL;
        cout<<"move construct!"<<endl;
    }
    ~demo(){
        cout<<"class destruct!"<<endl;
    }
private:
    int *num;
};
demo get_demo(){
    return demo();
}
int main(){
    demo a = get_demo();
    return 0;
}