【力扣周赛 338】
6354. K 件物品的最大和 - 力扣(Leetcode)
袋子中装有一些物品,每个物品上都标记着数字 1 、0 或 -1 。
给你四个非负整数 numOnes 、numZeros 、numNegOnes 和 k 。
袋子最初包含:
numOnes 件标记为 1 的物品。
numZeroes 件标记为 0 的物品。
numNegOnes 件标记为 -1 的物品。
现计划从这些物品中恰好选出 k 件物品。返回所有可行方案中,物品上所标记数字之和的最大值。
示例 1:
输入:numOnes = 3, numZeros = 2, numNegOnes = 0, k = 2 输出:2 解释:袋子中的物品分别标记为 {1, 1, 1, 0, 0} 。取 2 件标记为 1 的物品,得到的数字之和为 2 。 可以证明 2 是所有可行方案中的最大值。
示例 2:
输入:numOnes = 3, numZeros = 2, numNegOnes = 0, k = 4 输出:3 解释:袋子中的物品分别标记为 {1, 1, 1, 0, 0} 。取 3 件标记为 1 的物品,1 件标记为 0 的物品,得到的数字之和为 3 。 可以证明 3 是所有可行方案中的最大值。
提示:
0 <= numOnes, numZeros, numNegOnes <= 50
0 <= k <= numOnes + numZeros + numNegOnes
思路
easy等级的,比较简单。
要去到最大值,分别有以下3种情况:
全部是1
1和0混合
1、0和-1混合,因为 k <= numOnes + numZeros + numNegOnes,所以最后的值就是 1的个数减去我们需要的-1的个数(k - numOnes - numZeros)
代码实现
class Solution {
public int kItemsWithMaximumSum(int numOnes, int numZeros, int numNegOnes, int k) {
if(numOnes > k){
return k;
}else if(numOnes + numZeros > k){
return numOnes;
}else{
return numOnes - k + numOnes + numZeros;
}
}
}6355. 质数减法运算 - 力扣(Leetcode)
给你一个下标从 0 开始的整数数组 nums ,数组长度为 n 。
你可以执行无限次下述运算:
选择一个之前未选过的下标 i ,并选择一个 严格小于 nums[i] 的质数 p ,从 nums[i] 中减去 p 。
如果你能通过上述运算使得 nums 成为严格递增数组,则返回 true ;否则返回 false 。
严格递增数组 中的每个元素都严格大于其前面的元素。
示例 1:
输入:nums = [4,9,6,10] 输出:true 解释: 在第一次运算中:选择 i = 0 和 p = 3 ,然后从 nums[0] 减去 3 ,nums 变为 [1,9,6,10] 。 在第二次运算中:选择 i = 1 和 p = 7 ,然后从 nums[1] 减去 7 ,nums 变为 [1,2,6,10] 。 第二次运算后,nums 按严格递增顺序排序,因此答案为 true 。
示例 2:
输入:nums = [6,8,11,12] 输出:true 解释:nums 从一开始就按严格递增顺序排序,因此不需要执行任何运算。
示例 3:
输入:nums = [5,8,3] 输出:false 解释:可以证明,执行运算无法使 nums 按严格递增顺序排序,因此答案是 false 。
提示:
1 <= nums.length <= 1000
1 <= nums[i] <= 1000
nums.length == n
思路
首先,说一下踩到的坑。
严格小于 nums[i] 的质数 p。严格小于就是不包括等于,应该是 a < b,而不是 a <= b
每一个位置减去最佳的数(p)之后,记得break,跳出寻找最佳的数的循环。
然后就是这一题的思路。一看到这个题目,不知道怎么去找到每个位置最合适的p,因为后面的数,会因为前面的数受影响,而后面又注意到“选择一个之前未选过的下标 i”,所以每一个位置只可以减一次。所以我们就从头开始遍历,前面的变成最小的能够变成的数,如果还是不能变成严格递增的序列,那么这个序列不可能会变成严格递增的序列。
代码实现
class Solution {
public static boolean isPrime(int n) { //判断质数(素数)
if (n <= 3) {
return n > 1;
}
//判断一个数能否被小于sqrt(n)的数整除
int sqrt = (int)Math.sqrt(n);
for (int i = 2; i <= sqrt; i++) {
if(n % i == 0) {
return false;
}
}
return true;
}
public boolean check(int[] nums, int k){ //判断该序列是否严格递增
int flag = 0;
for(int i = k; i < nums.length - 1; i++){
if(nums[i] >= nums[i + 1]){
flag = 1;
break;
}
}
if(flag == 0){
return true;
}
return false;
}
public void find(int[] nums, int k){ //找到最合适的p
if(k == 0){ //序列第一位不受前面一位的影响,因为没有前面一位
if(nums[k] > 2){
for(int j = nums[k] - 1; j > 1; j--){
if(isPrime(j)){
nums[k] = nums[k] - j;
break;
}
}
}
}
else{
for(int j = nums[k] - 1; j > 1; j--){
if(isPrime(j) && nums[k] - j > nums[k - 1]){
nums[k] = nums[k] - j;
break;
}
}
}
}
public boolean primeSubOperation(int[] nums) {
if(check(nums, 0)){
return true;
}
for(int i = 0; i < nums.length; i++){
find(nums, i);
if(check(nums, 0)){
return true;
}
}
return false;
}
}6357. 使数组元素全部相等的最少操作次数 - 力扣(Leetcode)
给你一个正整数数组 nums 。
同时给你一个长度为 m 的整数数组 queries 。第 i 个查询中,你需要将 nums 中所有元素变成 queries[i] 。你可以执行以下操作 任意 次:
将数组里一个元素 增大 或者 减小 1 。
请你返回一个长度为 m 的数组 answer ,其中 answer[i] 是将 nums 中所有元素变成 queries[i] 的 最少 操作次数。
注意,每次查询后,数组变回最开始的值。
示例 1:
输入:nums = [3,1,6,8], queries = [1,5] 输出:[14,10] 解释:第一个查询,我们可以执行以下操作: - 将 nums[0] 减小 2 次,nums = [1,1,6,8] 。 - 将 nums[2] 减小 5 次,nums = [1,1,1,8] 。 - 将 nums[3] 减小 7 次,nums = [1,1,1,1] 。 第一个查询的总操作次数为 2 + 5 + 7 = 14 。 第二个查询,我们可以执行以下操作: - 将 nums[0] 增大 2 次,nums = [5,1,6,8] 。 - 将 nums[1] 增大 4 次,nums = [5,5,6,8] 。 - 将 nums[2] 减小 1 次,nums = [5,5,5,8] 。 - 将 nums[3] 减小 3 次,nums = [5,5,5,5] 。 第二个查询的总操作次数为 2 + 4 + 1 + 3 = 10 。
示例 2:
输入:nums = [2,9,6,3], queries = [10] 输出:[20] 解释:我们可以将数组中所有元素都增大到 10 ,总操作次数为 8 + 1 + 4 + 7 = 20 。
提示:
n == nums.length
m == queries.length
1 <= n, m <= 10 5
1 <= nums[i], queries[i] <= 10 9
思路
首次尝试,暴力超时。
然后,想到直接获取需要增加的次数以及减少的次数,两者相加即可。因此,想到了前缀和,得到小于该元素的所有元素和大于该元素的所有元素即可。但是我们还是得要去找到和queries最相近的数的位置,从而区分左右两边,所以我们需要用到二分查找
代码实现
class Solution {
public int binarySearch(int[] nums, int des){
//定义初始最小、最大索引
int low = 0;
int high = nums.length - 1;
//确保不会出现重复查找,越界
while (low <= high) {
//计算出中间索引值
int middle = (high + low) >>> 1;//防止溢出
if (des == nums[middle]) {
return middle;
//判断下限
} else if (des < nums[middle]) {
high = middle - 1;
//判断上限
} else {
low = middle + 1;
}
}
return -1;
}
public List minOperations(int[] nums, int[] queries) {
List list = new ArrayList<>();
Arrays.sort(nums);
int[] a = new int[nums.length];
for (int i = 0; i < nums.length; i++) { // 前缀和
if (i == 0) {
a[i] = nums[i];
} else {
a[i] = nums[i] + a[i - 1];
}
}
for (int i = 0; i < queries.length; i++) {
long sum = 0L;
if (nums[nums.length - 1] <= queries[i]) {
sum = nums.length * queries[i] - a[nums.length - 1];
} else if (nums[0] >= queries[i]) {
sum = a[nums.length - 1] - nums.length * queries[i];
} else {
// 定义初始最小、最大索引
int low = 0;
int high = nums.length - 1;
int index = 0;
// 确保不会出现重复查找,越界
while (low <= high) {
// 计算出中间索引值
int middle = (high + low) >> 1;// 防止溢出
if (queries[i] >= nums[middle]) {
index = middle;
low = middle + 1;
// 判断下限
} else if (queries[i] < nums[middle]) {
high = middle - 1;
// 判断上限
}
}
sum = queries[i] * (index + 1) - a[index] + a[nums.length - 1] - a[index] - queries[i] * (nums.length - index - 1);
}
list.add(sum);
}
return list;
}
} 6356. 收集树中金币 - 力扣(Leetcode)
给你一个 n 个节点的无向无根树,节点编号从 0 到 n - 1 。给你整数 n 和一个长度为 n - 1 的二维整数数组 edges ,其中 edges[i] = [a i, b i] 表示树中节点 a i 和 b i 之间有一条边。再给你一个长度为 n 的数组 coins ,其中 coins[i] 可能为 0 也可能为 1 ,1 表示节点 i 处有一个金币。
一开始,你需要选择树中任意一个节点出发。你可以执行下述操作任意次:
收集距离当前节点距离为 2 以内的所有金币,或者
移动到树中一个相邻节点。
你需要收集树中所有的金币,并且回到出发节点,请你返回最少经过的边数。
如果你多次经过一条边,每一次经过都会给答案加一。
示例 1:
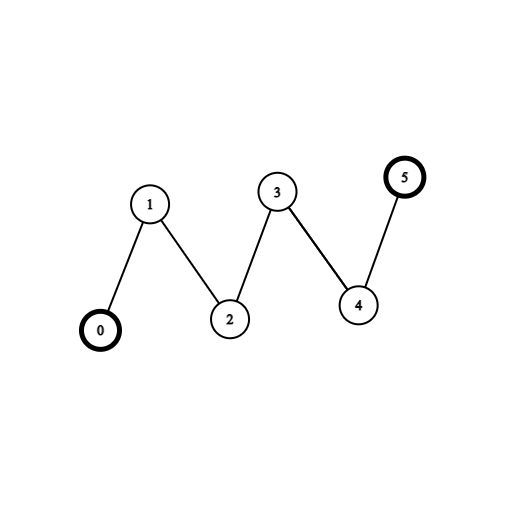
输入:coins = [1,0,0,0,0,1], edges = [[0,1],[1,2],[2,3],[3,4],[4,5]] 输出:2 解释:从节点 2 出发,收集节点 0 处的金币,移动到节点 3 ,收集节点 5 处的金币,然后移动回节点 2 。
示例 2:
输入:coins = [0,0,0,1,1,0,0,1], edges = [[0,1],[0,2],[1,3],[1,4],[2,5],[5,6],[5,7]] 输出:2 解释:从节点 0 出发,收集节点 4 和 3 处的金币,移动到节点 2 处,收集节点 7 处的金币,移动回节点 0 。
提示:
n == coins.length
1 <= n <= 3 * 10 4
0 <= coins[i] <= 1
edges.length == n - 1
edges[i].length == 2
0 <= a i, b i < n
a i != b i
edges 表示一棵合法的树。