高完整性系统工程（三）： Logic Intro & Formal Specification

目录

1. Propositions 命题

 2.1 Propositional Connectives 命题连接词 

2.2 Variables 变量

2.3 Sets

 2.3.1 Set Operations

2.4 Predicates 

2.5 Quantification 量化

2.6 Relations

2.6.1 What Is A Relation?

2.6.2 Relations as Sets

2.6.3 Binary Relations as Pictures

2.6.4 Relation Example

2.6.5 Functions

2.6.6 Total vs Partial Functions 全函数 VS 部分函数

2.6.7 Relation Operations

2.6.8 Relation Joins 

3. TEMPORAL LOGIC 时序逻辑

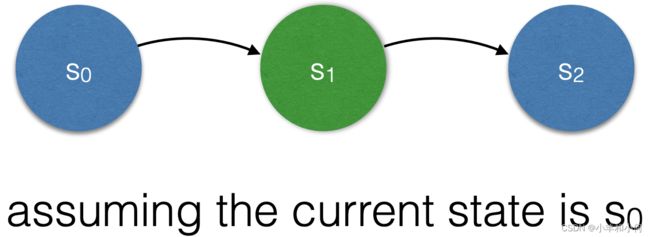
3.1 Next State

3.1.1 Transitions and Traces

3.2 Temporal Operators 时间运算符

4. SPECIFICATIONS SAY “WHAT” DESIGNS SAY “HOW” 

4.1 Specifying Software

4.2 Aside: Functions as Relations

4.3 Modelling Data Types 

4.4 Sequences as Relations  作为关系的序列

4.5 Searching

4.6 Pre and Postconditions 前置条件和后置条件

4.7 Formal Model-Based Specs

4.8 Advantages

4.9 Effect on Cost

4.10 Disadvantages

4.11 Difficulty

5. SPECIFICATIONS IN ALLOY

5.1 Alloy

6. LASTPASS DEMO

6.1 Alloy Modelling Overview

---

1. Propositions 命题

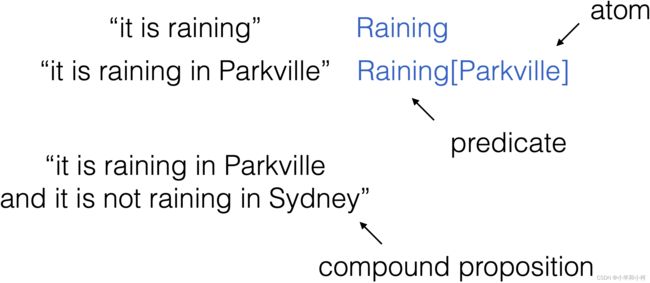
定义：A statement that is either true or false

 2.1 Propositional Connectives 命题连接词 

2.2 Variables 变量

Variables allow propositions to talk about state

Variables talk about different parts of the state of the formal model. (not state of the system/program)

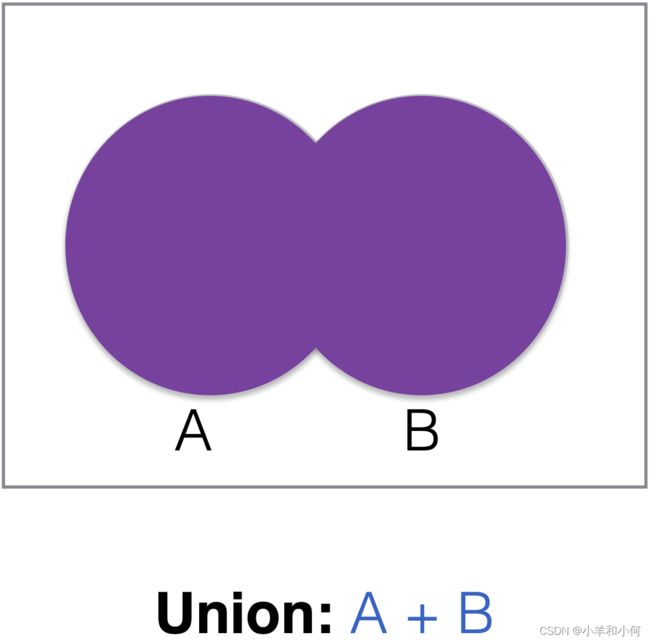
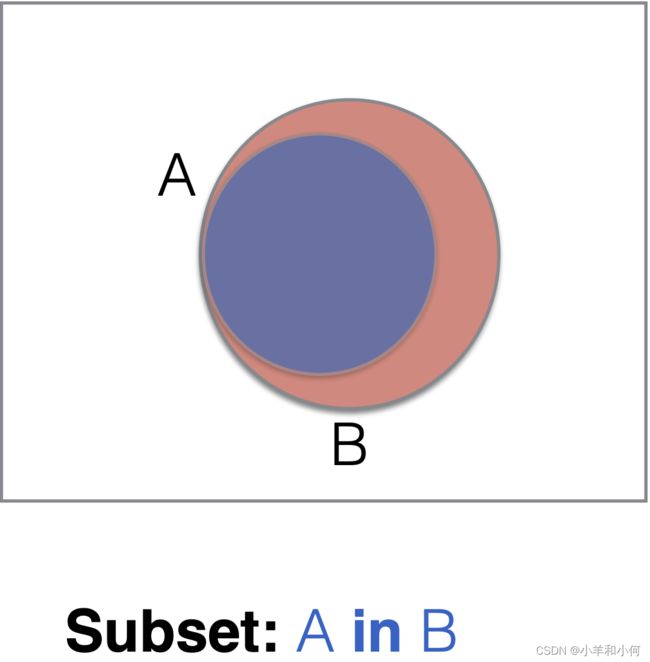
2.3 Sets

A collection of things

 2.3.1 Set Operations

2.4 Predicates 

Extend propositions with the ability to quantify the values of a variable that a proposition is true for

all: Proposition P(x) holds for all values of x 

all x | P[x]

all city | Raining[city]

all city: AustralianCities | Raining[city]

some: Proposition P(x) holds for at least one value of x

some x | P[x]

some city | not Raining[city]

2.5 Quantification 量化

De Morgan’s Laws

all x | P[x]         is equivalent to         not some x | not P[x]

some x | P[x]    is equivalent to         not all x | not P[x]

Alloy Specific Quantifiers

one x | P[x] P(x)         holds for exactly one value x

lone x | P[x] P(x)        holds for at most one value x

none x | P[x] P(x)       holds for no value x

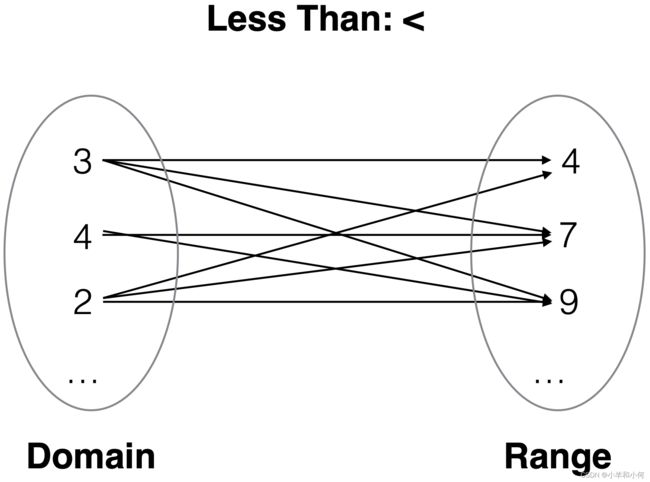
2.6 Relations

A proposition that relates things together =, <, etc.

arity: the number of things the relation relates =, < etc. are all binary relations; relate two numbers 3 < 4, (5 - 1) = (3 + 1), etc.

A relation that relates three things together: IsSum(x,y,z) <=> z = x + y

Relations are just predicate

2.6.1 What Is A Relation?

How would you write down unambiguously what a relation means?

Simplest answer: just list all of the things it relates together.

Any relation is a simply a set of tuples. 

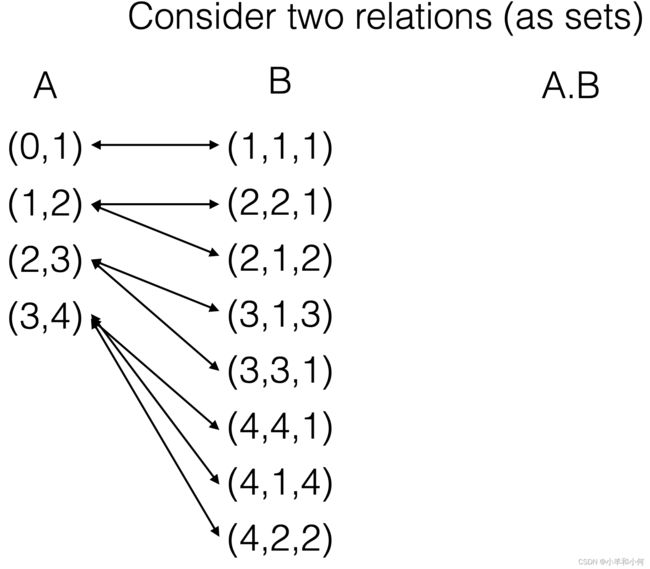
2.6.2 Relations as Sets

Factor(x,y,z) — {(x,y,z) | x = y * z}

{(1,1,1), (2,1,2), (2,2,1), (3,1,3), (3,3,1),(4,4,1), (4,2,2),…}

Use Factor to define when a number is prime, i.e. define the predicate IsPrime[x] 使用Factor来定义一个数字何时是质数，即定义谓词IsPrime[x]。

all y,z | (x,y,z) in Factor implies y = 1 or z = 1

A relation with arity n (i.e. an n-ary relation) R, is a set of n-tuples of atoms. 一个有n个算数的关系（即n-ary关系）R，是一个由n个原子图元组成的集合。

A binary (2-ary) relation R(a,b) is a set of:                 pairs

A ternary (3-ary) relation R(a,b,c) is a set of:             triples

A unary (1-ary) relation R(a) is a set of:                     atoms

Sets are relations, and relations are sets. 集合是关系，而关系是集合。

Sets are predicates, and predicates are sets. 集合是谓词，而谓词是集合。

Relations are predicates, and predicates are relations. 关系是谓词，而谓词是关系。

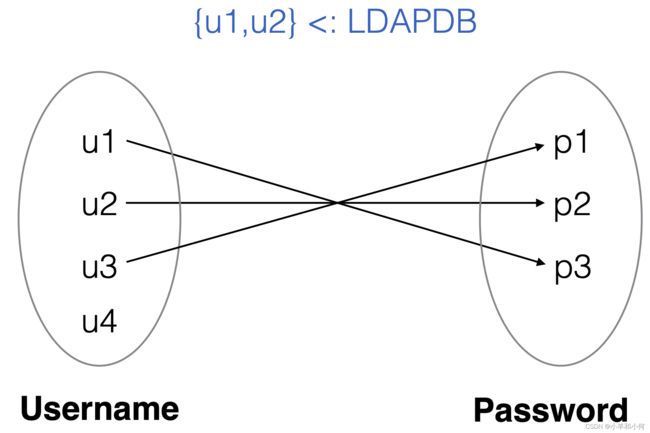
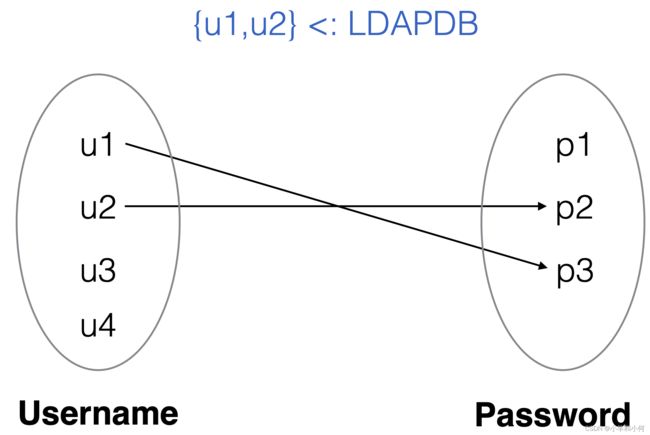
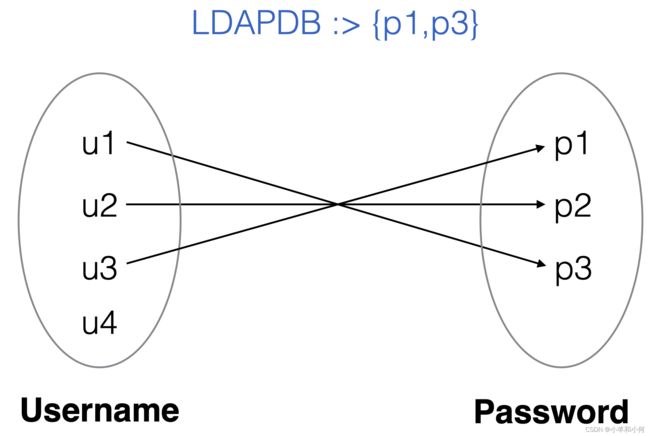
2.6.3 Binary Relations as Pictures

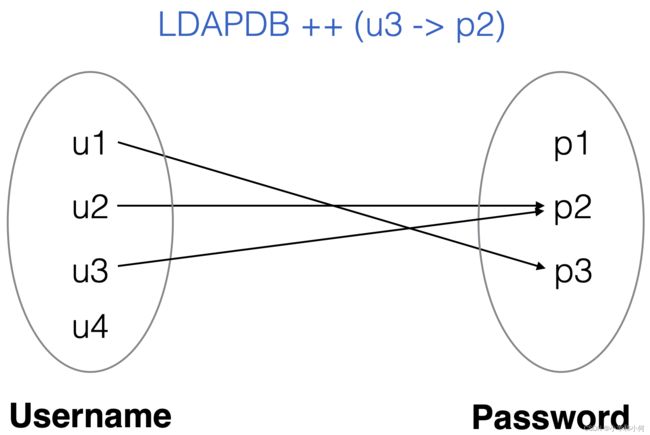
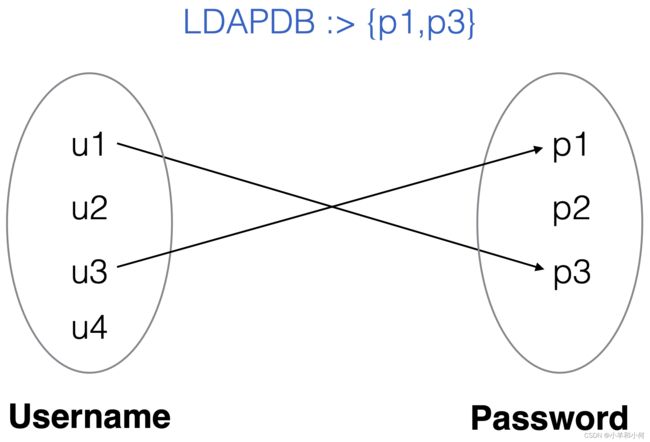
2.6.4 Relation Example

Imagine 2 sets of atoms:

Username = {n1, n2, …}

Password = {p1, p2, …}

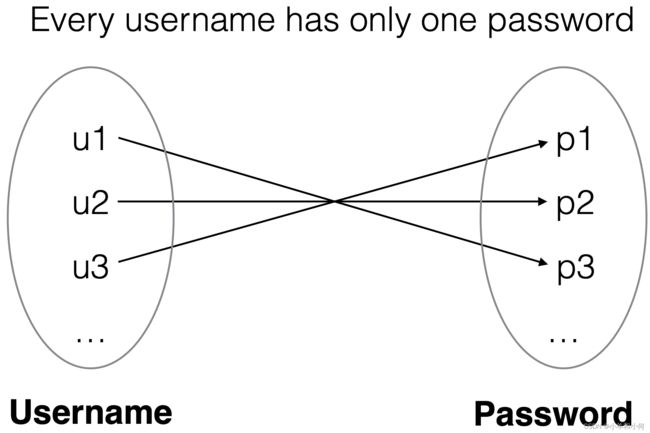
Imagine an LDAP username/password database.

LDAPDB : Username -> Password

LDAPDB ⊆ (Username x Password)

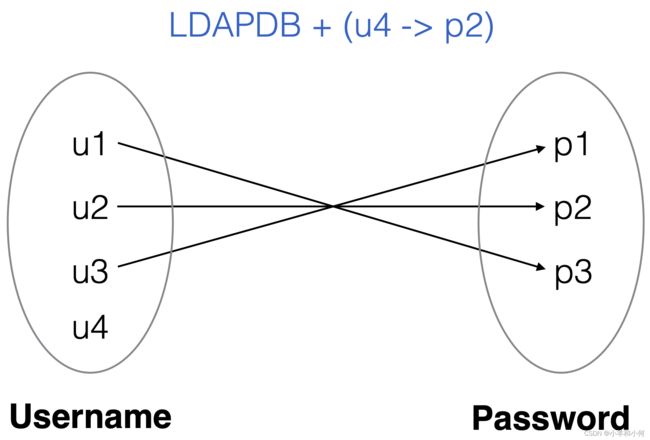
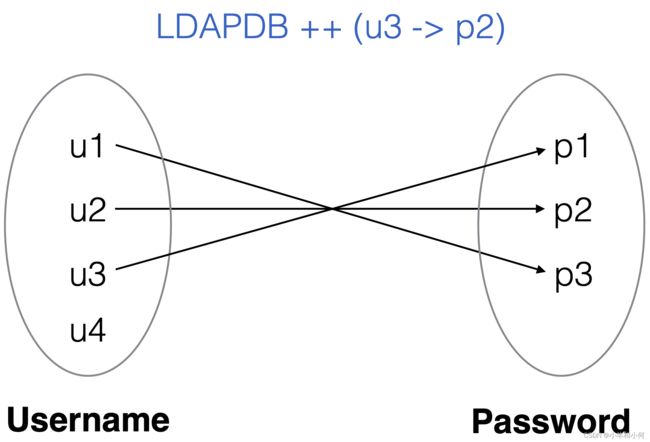
2.6.5 Functions

For every username, there is only one password in LDAPDB

all u:Username, pw1:Password, pw2:Password | LDAPDB(u,pw1) and LDAPDB(u,pw2) implies pw1 = pw2

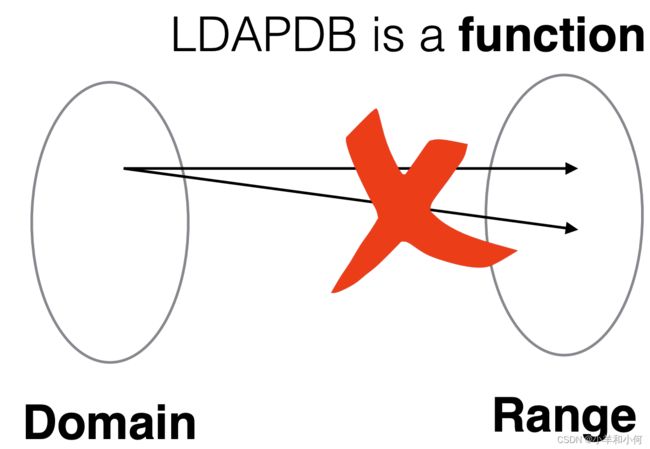
2.6.6 Total vs Partial Functions 全函数 VS 部分函数

LDAPDB : Username -> Password

Does every username in Username have a password?

A total function gives an answer for every (type-correct) argument

A partial function is one that is not total

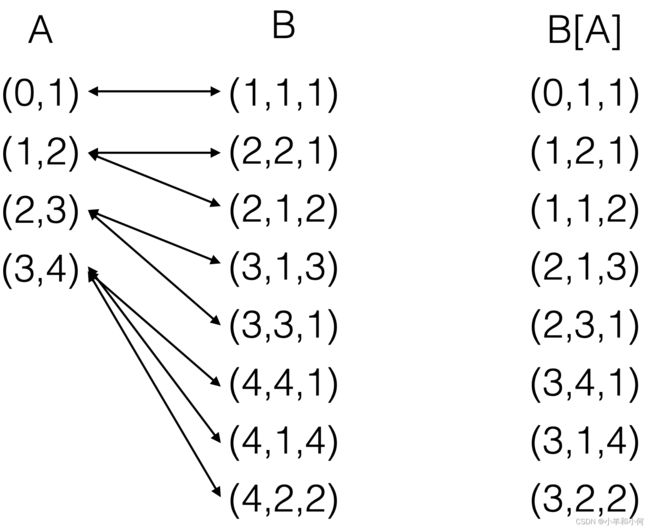
2.6.7 Relation Operations

 

xQ

2.6.8 Relation Joins 

3. TEMPORAL LOGIC 时序逻辑

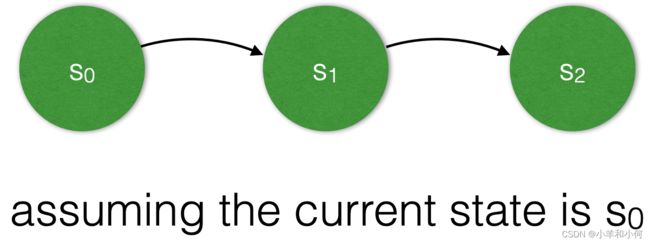
3.1 Next State

if x is a variable, then x’ refers to x’s value in the next state 如果x是一个变量，那么x'指的是x在下一个状态中的值

To specify that x is incremented, we would write 要指定x被递增，我们可以写成

x’ = x + 1

Predicates that talk about x are also allowed to talk about x’s value in future states, e.g. x’, x’’ etc. and how it relates to x’s current value 谈论x的谓词也被允许谈论x在未来状态下的价值，例如x'，x''等，以及它与x的当前价值的关系。

These predicates define state transitions 这些谓词定义了状态转换

3.1.1 Transitions and Traces

3.2 Temporal Operators 时间运算符

We can also write predicates that talk about future and even past states using temporal operators 我们还可以使用时间运算符编写谈论未来甚至是过去状态的谓词

always P

after P

eventually P

P; Q

equivalent to P and (after Q)

4. SPECIFICATIONS SAY “WHAT” DESIGNS SAY “HOW” 

4.1 Specifying Software

Specify modules

Formally describe (an abstraction of) the module’s state 正式描述（抽象的）模块的状态

Formally describe the behaviour of the module’s operations (e.g. procedures, functions etc.). 正式描述模块的操作行为（如程序、函数等）

Behaviour specified in terms of state (transition) relations. 用状态（转换）关系来指定行为。

Trivial example:                  a counter

State: natural number         n : ℕ

Operation: increment         n’ = n+1

4.2 Aside: Functions as Relations

4.3 Modelling Data Types 

Data types modelled as sets, relations, functions etc. 以集合、关系、函数等为模型的数据类型。

4.4 Sequences as Relations  作为关系的序列

4.5 Searching

4.6 Pre and Postconditions 前置条件和后置条件

Precondition: Specifies the assumptions made by a procedure/function 前提条件。指明一个程序/函数所做的假设

Postcondition: Specifies the behaviour, assuming that the precondition holds 后置条件。指定行为，假设前提条件成立

Precondition for binary search: list is sorted 二进制搜索的前提条件：列表被排序

sorted(list) <=> all i : ℤ | i < #list implies list[i] ≤ list[i+1]

4.7 Formal Model-Based Specs

Model the behaviour of each operation as a relation 将每个操作的行为建模为一种关系

The relation captures the relationship between the operation’s inputs and outputs 该关系捕捉到操作的输入和输出之间的关系

In general: relates the states before and after the operation 一般来说：将操作前后的状态联系起来

Says how they are allowed to differ (postcondition) under assumptions about the inputs (precondition) 说出了在关于输入（前提条件）的假设下允许它们有什么不同（后置条件）

Says what the operation does, not how it does it. 说的是操作做什么，而不是它如何做

4.8 Advantages

• Small
• Unambiguous
• Abstract from Implementation
• Machine-Checkable
• Forces thinking up-front
• Gets mistakes out of the way early (i.e. when they are cheaper to fix)
• 小型
• 毫不含糊
• 从实现中抽象出来
• 可由机器检查
• 迫使人们提前思考
• 尽早消除错误（即当它们的修复成本较低时）。

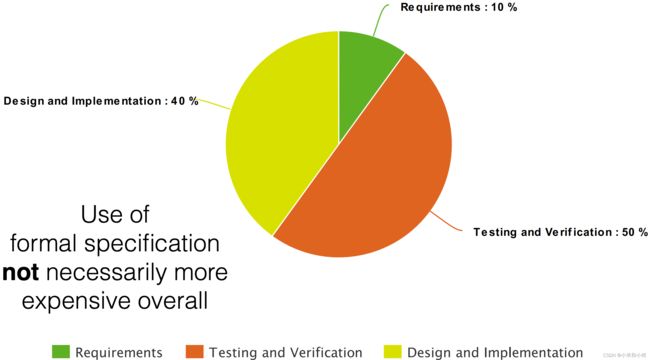
4.9 Effect on Cost

4.10 Disadvantages

• Requires specialised expertise 需要专门的专业知识
• Might lengthen time to implementation 可能会延长实施的时间
• Loads more effort early in the development process 在开发过程的早期要付出更多的努力
• Not necessarily well suited to projects with rapidly changing requirements. 不一定很适合于需求快速变化的项目
• (So it’s important to get your HAZOP etc. correct) (所以，正确地进行HAZOP等是很重要的）

4.11 Difficulty

All programmers know many formal languages 所有的程序员都知道许多形式语言

Specs are shorter and thus simpler to write than code 规范更短，因此比代码更容易编写

Specs say only what not how 规范只说什么，不说怎么做

Programs must say both 程序必须说明这两点

Ordinary programmers not trained to write and read formal specs 普通程序员没有受过编写和阅读正式规范的训练

5. SPECIFICATIONS IN ALLOY

5.1 Alloy

6. LASTPASS DEMO

6.1 Alloy Modelling Overview

signatures: declaring sets and relations 声明集合和关系

facts: axioms that hold over signatures and globally constrain the model to rule out nonsense 适用于签名的公理，并在全局上约束模型以排除无意义的东西

predicates: define relations between variables in a model, used to specify operations, state transitions 定义模型中变量之间的关系，用于指定操作和状态转换

functions: shorthand for expressions 表达式的简写