树状数组或二叉索引树（Binary Indexed Tree）

1. 前言

树状数组或二叉索引树（Binary Indexed Tree），又以其发明者命名为 Fenwick 树。其初衷是解决数据压缩里的累积频率的计算问题，现多用于高效计算数列的前缀和、区间和。它可以以 O(logn) 的时间得到任意前缀和。并同时支持在 O(logn) 时间内支持动态单点值的修改。空间复杂度 O(n)。

2. 树状数组

代码实例：

int lowbit(int i)
{
    return i & -i;//或者是return i-(i&(i-1));表示求数组下标二进制的非0最低位所表示的值
}
void update(int i,int val)//单点更新
{
    while(i<=n){
        C[i]+=val;
        i+=lowbit(i);//由叶子节点向上更新树状数组C，从左往右更新
    }
}
int sum(int i)//求区间[1,i]内所有元素的和
{
    int ret=0;
    while(i>0){
        ret+=C[i];//从右往左累加求和
        i-=lowbit(i);
    }
    return ret;
}

lowbit(n)函数取出n在二进制表示下最低位的1以及它后面的0构成的数值，如：lowbit(110) = 010，其中110十进制为6，010十进制为2

3. 实现原理

模板中最常见的三个函数：①取数组下标二进制非0最低位所表示的值；②单点更新；③区间查询。树状数组，顾名思义是树状的数组，我们首先引入二叉树，叶子节点代表A[1]~A[8]。

现在变形一下：

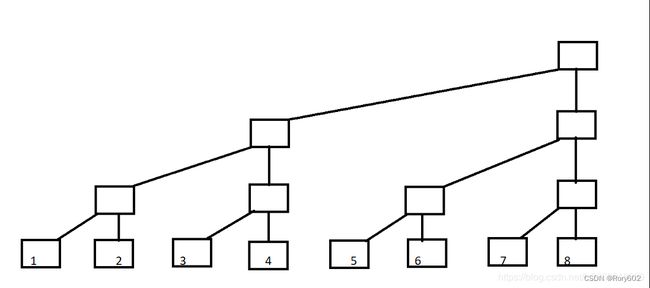
现在定义每一列的顶端节点C数组（其实C数组就是树状数组），如图：

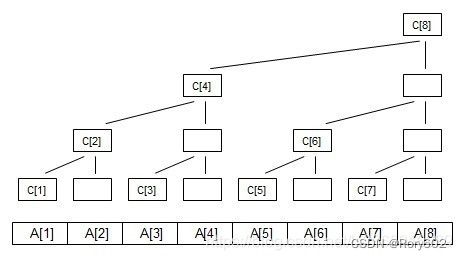
1. 数组生成
理解树状数组的重点

C[i]代表子树的叶子节点的权值之和，如图可以知道：

• C[1]=A[1];
• C[2]=A[1]+A[2];
• C[3]=A[3];
• C[4]=A[1]+A[2]+A[3]+A[4];
• C[5]=A[5];
• C[6]=A[5]+A[6];
• C[7]=A[7];
• C[8]=A[1]+A[2]+A[3]+A[4]+A[5]+A[6]+A[7]+A[8];

设节点编号为$i$，那么这个节点管辖的区间为$2^k$（其中$k$为$i$二进制末尾0的个数，即$2^k$表示$i$的二进制最后一位1代表的数）个元素。因为这个区间最后一个元素必然为$A[i]$，所以很明显：$C[n]=A[n–2^k+1]+...+A[n]$，算这个$2^k$的值有一个快捷的办法，定义一个函数如下即可：
利用机器补码特性：

int lowbit(int x)
　　{
　　　　return x&(-x);
　　}

例：计算C[6]
6的二进制表示为0110
-6的二进制表示为1010（6的补码）
则 　　
$$\begin{array}{lc}& 0110\\ \&& 1010\\ & 0010\end{array}$$
二进制0010的十进制为2，表示C[6]节点管理的区间为2， C[6] = A[5] + A[6]
　　
2. 区间查询（求和）

利用C[i]数组，求A数组中前i项和，举两个例子：
①i=7，前7项和：sum[7]=A[1]+A[2]+A[3]+A[4]+A[5]+A[6]+A[7]；

由于C[4]=A[1]+A[2]+A[3]+A[4]；C[6]=A[5]+A[6]；C[7]=A[7]；可以得到：sum[7]=C[4]+C[6]+C[7]。
数组下标写成二进制：sum[(111)]=C[(100)]+C[(110)]+C[(111)]；

②i=5，前5项和：sum[5]=A[1]+A[2]+A[3]+A[4]+A[5]；

由于C[4]=A[1]+A[2]+A[3]+A[4]；C[5]=A[5]；可以得到：sum[5]=C[4]+C[5]；
数组下标写成二进制：sum[(101)]=C[(100)]+C[(101)]；

细细观察二进制，树状数组追其根本就是二进制的应用，结合代码演示一下代码过程：

int sum(int i)//求区间[1,i]所有元素的和
{
    int ret=0;
    while(i>0){
        ret+=C[i];//从右往左区间求和
        i-=lowbit(i);
    }
    return ret;
}

当想要查询一个sum(n)(求A[n]的和），可以依据如下算法即可：
step1:　令sum = 0，转第二步；
step2:　假如i <= 0，算法结束，返回sum值，否则sum = sum + C[i]，转第三步；
step3: 令i = i – lowbit(i)，转第二步。(i = i – lowbit(i)这一步实际上等价于将i的二进制的最后一个1减去。)
可以看出，这个算法就是将这一个个区间的和全部加起来，为什么是效率是log(n)的呢？
以下给出证明：
i = i – lowbit(i)这一步实际上等价于将i的二进制的最后一个1减去。而i的二进制里最多有log(n)个1，所以查询效率是log(n)

示例1： 对于i=7进行演示
B：二进制的后缀
D：十进制的后缀

// 求和值： 7(111B)
//二进制循环的过程： 111B > 110B > 100B， 每次删除最后一个1，然后进行求和
// 第1轮循环
7D = 111B 
ans+= 111B 
lowbit(111B)=001B 
111B-lowbit(111B)=110B //二进制表示， 110B的十进制为6, 7D-lowbit(7D)=6D
 
// 第2轮循环
ans+=C[110B] //二进制表示,C[110B]=C[6D]
lowbit(110B)=010B 
110B-lowbit(110B)=100B //二进制表示，100B的十进制为4, 6D-lowbit(6D)=4D

// 第3轮循环
ans+=C[100B] //二进制表示C[100B]=C[4D]
lowbit(100B)=100B //二进制表示，100B的十进制为4
100B-lowbit(100B)=000B // 4D-lowbit(4D) = 0D

// 第4轮循环
break；

示例2： 对于i=5进行演示

//求和值： 5(101)  
//二进制循环的过程： 101 > 100
// 第1轮循环
5D = 101B
ans+=C[101B]
lowbit(101B)=001B
101B-lowbit(101B)=100B //100B的十进制为4 5D-lowbit(5D)=4D
 
// 第2轮循环
ans+=C[100B]
lowbit(100B)=100B //100B的lowbit为它本身
100B-lowbit(100B)=000B // 4D-lowbit(4D) = 0D

// 第3轮循环
break；

3. 单点更新

当我们修改A数组中某个值时，应当如何更新C数组呢？回想一下，区间查询的过程，再看一下上文中列出的过程。这里声明一下：单点更新实际上是不修改A数组的，而是修改树状数组C，向上更新区间长度为lowbit(i)所代表的节点的值。

void update(int i,int val)//更新单节点的值
{
    while(i<=n){
        C[i]+=val;
        i+=lowbit(i);//由叶子节点向上更新a数组
    }
}
//可以发现 更新过程是查询过程的逆过程
//由叶子结点向上更新C[]数组

修改一个节点，必须修改其所有祖先，最坏情况下为修改第一个元素，最多有log(n)个祖先
所以修改算法如下（给某个结点i加上x）：
step1: 当i > n时，算法结束，否则转第二步；
step2: C[i] = C[i] + val， i = i + lowbit(i)转第一步。
（i = i +lowbit(i)这个过程实际上也只是一个把末尾1补为0的过程）
示例1：以A[5]增加val值

//C的索引值每次增加lowbit值
5D = 101B 
lowbit(101B)=001B 
101B + 001B = 110B //110十进制为6 5D + lowbit(5D) = 6D
lowbit(110B) = 010B 
110B + 010B = 1000B //1000十进制为8 6D + lowbit(6D) = 8D

4.求区间和

/// 

/// 计算索引值从start到end的元素之和
/// 
/// 起始元素索引值
/// 结尾元素索引值
/// 
int sum_StartToEnd(int start, int end)
 {
	if (start == 0)
     {
         return sum(end);
     }
     return sum(end) - sum(start - 1);
  }

参考资料：
https://blog.csdn.net/ls2868916989/article/details/119268741
https://www.cnblogs.com/Lehman-Share/p/8004983.html