Raki的读paper小记：Neuro-Inspired Stability-Plasticity Adaptation for Continual Learning in Sparse Nets

Abstract&Introduction&Related Work

• 研究任务
  Continual Learning
• 已有方法和相关工作
• 面临挑战
• 创新思路
  • 利用持续学习过程中的持续稀疏性，与使用密集架构的主流实践不同，我们从稀疏网络开始，并在整个学习轨迹中保持相同的连接密度
  • 受 “学习通过同时改变连接权重和网络结构在大脑中发生” 的启发，当学习新任务时，连接rewiring，以创建新的并修剪网络中的现有路径，rewiring过程有两个目标：解开干扰单元以避免遗忘，并创造新的途径来编码新知识
  • 禁用某些隐藏单元输入的梯度更新以保留先前学习的知识，受持续的树突棘的激励，通过“冻结”这些单元的传入连接来创建稳定的隐藏单元。因此，对于每个学习的任务，选择一小组保持稳定的单元，以避免忘记该任务
  • 保持固定容量模型（固定数量的层和单元），即使通过rewiring架构是动态的，NISPA不需要模型扩展。它将知识依次累积到一组固定的隐藏单元中
  • 与其依赖生物学上不可信的排练机制来缓解CF，不如在DNN的动态架构中嵌入新知识，与睡眠和记忆巩固类似，NISPA在训练期间需要一些时间来确定哪些路径对于记忆新任务至关重要，以及是否可以在不干扰先前任务的情况下添加新路径
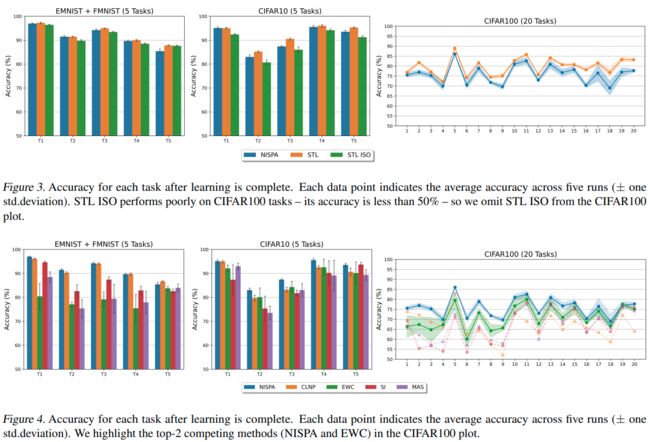
• 实验结论
  从计算角度来看，NISPA只使用每个单元一个额外的位来标记该单元是稳定的还是塑性的。此外，由于稀疏性和rewiring，与sota相比，它需要更少的参数来实现更好的性能，它使用的可学习参数也少了十倍
  提出了一个用于类增量学习的NISPA扩展，其中在测试期间不提供任务标签。不幸的是，该扩展需要存储和回放以前类中的几个示例

NISPA

每个任务的训练分为“阶段”（每个阶段为e个阶段）。在连续阶段之间，选择候选稳定单元，然后进行rewiring

在任务边界上，候选稳定单元被提升为稳定单元，稳定单元之间的连接被冻结，然后我们重新初始化剩余的连接

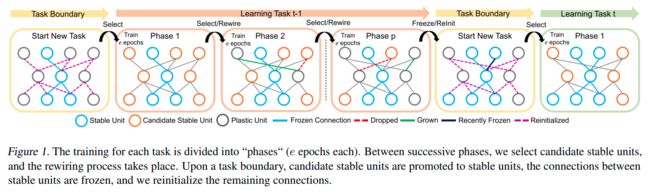
每个任务的训练分为“阶段”（每个阶段e个阶段），在每个阶段之后，我们选择候选稳定单元，该选择步骤之后是连接rewiring，在几个阶段重复该选择和rewiring循环，直到满足停止标准，当任务结束，我们将候选单元提升为稳定单元，冻结所有稳定单元的传入连接，并重新初始化可塑单元的权重

伪代码：

Notation and Problem Formulation

一共有 $T$ 个任务

第 $t$ 个任务，有训练集 $D_t$ 和验证集$V_t$

$l\in \{1,...,L\}$ 有$N_l$ 个单元，$n_i^l\left(i\in \{1,\dots ,N_l\}\right)$ 是该层的第 $i$ 个单元，${\theta }_{i,j}^l$ 代表 $n_j^{l-1}$ 到 $n_i^l$ 的第 $j$ 个连接

NISPA在整个训练过程中保持一定的连接密度d。密度d被定义为修剪之后和修剪之前的连接数量之间的比率。修剪是在初始化时随机执行的，并基于每个层执行，也就是每一层都具有相同的密度d

在卷积神经网络（CNN）中，一个“单元”被3D卷积核所代替，“连接”被2D卷积核所代替

Stabilizing a Plastic Unit

单元 $n_i^l$ 的激活由其父单元的激活和来自这些父单元的传入连接的权重决定。因此，训练期间的任何权重更新都会以两种方式改变单元 $n_i^l$ ：

1. 直接改变单元中传入连接的权重
2. 间接地，通过改变到单元祖先单元的传入连接的权重，即从输入到 $n_i^l$ 的任何路径中的单元
   NISPA使用连接rewiring确保稳定单元仅接收来自其他稳定单元的输入

在两个任务之间的边界处，它将连接冻结到新的稳定单元中以稳定这些单元，即它不允许相应的权重在该点之后发生变化

Selecting Candidate Stable Units

在任何给定的时间，层 $l$ 的单位 $U^l$ 被划分为三个不相交的集合：$S_c^l,S^l\text{and}{P}^l$，即候选稳定、稳定和可塑性单元。在学习任务 $t$ 时，NISPA周期性地将一些可塑单元从 $P^l$ 转换到候选（稳定）单位集合$S_c^l$ 。在该任务的训练结束时，$S_c^l$的成员晋升为$S^l$
假设我们从从上一个任务继承的集合 $P^l$ 和 $S^l$ 开始（如果没有上一任务，所有单元都是可塑的）
首先，我们计算该任务的所有训练示例中每个层的总激活，如下所示：

$A_l=\sum _{x\in D_t}{a}_l(x)=\sum _{x\in D_t}\sum _{i=1}^{N_l}{a}_{n_i^l}(x)(1)$

接下来，对于每个层，我们如下选择候选稳定单元 $S_c^l$：

min ⁡ S c ′ ⊆ P l ∣ S c l ∣ subject to ∑ x ∈ D t ∑ n l ′ ∈ S c l ∪ S l a n i ′ ( x ) ≥ τ A l ( 2 ) \begin{aligned}\min\limits_{S_c'\subseteq P^l}\left|S_c^l\right|\text{subject to}\sum\limits_{x\in D_t} \sum_{n_l'\in S_c^l\cup S^l}a_{n_i'}(x)\geq\tau A_l(2)\\ \end{aligned} Sc′​⊆Plmin​ ​Scl​ ​subject tox∈Dt​∑​nl′​∈Scl​∪Sl∑​ani′​​(x)≥τAl​(2)​

Calculating $\tau$

为了稳定训练，选择合适的温度参数

${\tau }_p=\frac{1}{2}\left(1+\cos \left(\frac{p\times \pi }{k}\right)\right)(3)$

其中p是相位数，k（通常为30或40）是决定函数形状的超参数

Skewness of activations

是否会选择太多的单元作为稳定单元，而没有为后续任务留下足够的可塑单元？
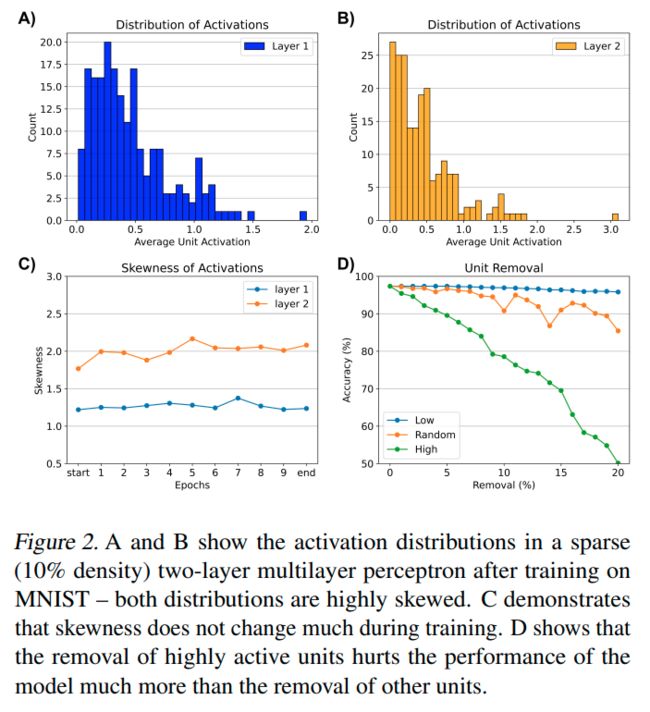
之前的工作观察到，使用ReLU导致每层激活分布在不同的网络架构和数据集之间高度偏斜。这种偏斜的主要原因是ReLU将所有负的预激活映射为零。因此，大多数单元的激活几乎为零，而只有少数单元具有较大的激活值。
图2-A，B显示了MNIST分类任务中这种现象的示例
图2-C显示，即使在第一个时期，激活分布的偏度（每层一个）也很高，并且在整个训练期间保持较高
这是NISPA的一个重点，因为它表明我们可以通过从分布的右尾部仅选择几个单元（即最活跃的单元）来满足τ约束

Activation as a Measure of Importance

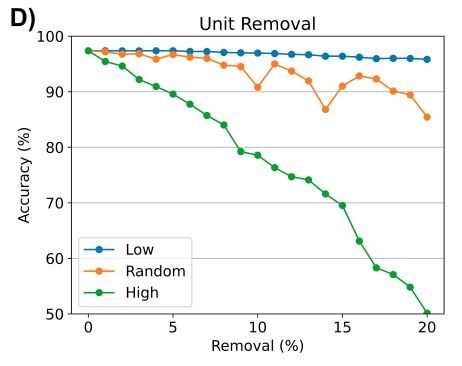
单元的总激活是否是其对学习任务的贡献的有效指标，观察到移除最活跃的单元比移除相同数量的随机选择单元更会降低性能

MNIST分类任务的类似结果如图2-D所示，突出了单元的激活与其对给定任务的重要性之间的强相关性

Connection Rewiring

NISPA利用连接rewiring有两个原因：减轻遗忘和创造新的正向转移途径
在每个阶段结束时，rewiring遵循候选稳定单元 $S_c^l$ 的选择，包括

1. dropping

2. growing connections,

3. 我们移除了从可塑单元到（可能是候选）稳定单元的连接。因此可塑单元的功能的未来变化不会传播到稳定单元

4. 从层 $l$ 中删除一些连接之后，在层 $l$ 中增加相同数量的新连接，保持每层的密度，新的连接是随机选择的，只要它们不形成稳定单元的新输入，这保证了连接增长不会破坏稳定单元学习的表示。

新的连接用高斯分布来初始化

NISPA仅在两个可塑单元之间（type1），或从（可能候选）稳定单元到可塑单元（type2）之间建立连接
type1和type2连接用于不同的目的：

1. type1连接可以使学习未来任务的新表示成为可能
2. type2连接促进了正向传递，因为可塑单元可以利用学习和稳定的表示根据任务之间的相似性以及添加连接的层，类型1可能比类型2更有价值

Stopping criterion

阶段数不是固定的
如果新的精度比旧的差，直接回溯，在phase级别而不是epoch级别执行早停
任务的训练以e个phase的最终序列结束。这允许网络从上次rewiring过程造成的任何性能损失中恢复。我们观察到，可塑单元从上一个任务的训练开始就有偏差，这阻碍了学习新任务。因此，在开始新任务的训练之前，我们重新初始化所有未冻结连接的权重

Experiments

Conclusions

NISPA是一种神经启发的持续学习方法，这是第一种在整个学习轨迹中使用恒定密度稀疏网络的方法。将稀疏性与rewiring相结合

Remark

稀疏但是保持参数量的思想不错，但是感觉实战有点难work