算法导论 — 3.2 标准记号与常用函数
笔记
1. 向下取整与向上取整
⌊ x ⌋ ⌊x⌋ ⌊x⌋是对 x x x向下取整,表示小于或等于 x x x的最大整数。 ⌈ x ⌉ ⌈x⌉ ⌈x⌉是对 x x x向上取整,表示大于或等于 x x x的最小整数。向下取整与向上取整具有以下规律:
(1) 对所有实数 x x x,有 x − 1 < ⌊ x ⌋ ≤ x ≤ ⌈ x ⌉ < x + 1 x-1<⌊x⌋≤x≤⌈x⌉<x+1 x−1<⌊x⌋≤x≤⌈x⌉<x+1
(2) 对任意整数 n n n,有 ⌈ n / 2 ⌉ + ⌊ n / 2 ⌋ = n ⌈n/2⌉+⌊n/2⌋=n ⌈n/2⌉+⌊n/2⌋=n
(3) 对任意实数 x ≥ 0 x ≥ 0 x≥0和整数 a , b > 0 a, b > 0 a,b>0,有
⌈ ⌈ x / a ⌉ b ⌉ = ⌈ x a b ⌉ ⌈\frac{⌈x/a⌉}{b}⌉=⌈\frac{x}{ab}⌉ ⌈b⌈x/a⌉⌉=⌈abx⌉
⌊ ⌊ x / a ⌋ b ⌋ = ⌊ x a b ⌋ ⌊\frac{⌊x/a⌋}{b}⌋=⌊\frac{x}{ab}⌋ ⌊b⌊x/a⌋⌋=⌊abx⌋
⌈ a b ⌉ ≤ a + ( b − 1 ) b ⌈\frac{a}{b}⌉≤\frac{a+(b-1)}{b} ⌈ba⌉≤ba+(b−1)
⌊ a b ⌋ ≥ a − ( b − 1 ) b ⌊\frac{a}{b}⌋≥\frac{a-(b-1)}{b} ⌊ba⌋≥ba−(b−1)
(4) 向下取整函数 f ( x ) = ⌊ x ⌋ f(x)=⌊x⌋ f(x)=⌊x⌋是单调递增的,向上取整函数 f ( x ) = ⌈ x ⌉ f(x)=⌈x⌉ f(x)=⌈x⌉也是单调递增的。
2. 模运算
对任意整数 a a a和任意正整数 n n n,模运算 a m o d n a\ {\rm mod}\ n a mod n的结果就是 a a a除以 n n n的余数,即
a m o d n = a − n ⌊ a / n ⌋ a\ {\rm mod}\ n=a-n⌊a/n⌋ a mod n=a−n⌊a/n⌋
模运算的结果满足 0 ≤ a m o d n < n 0≤a\ {\rm mod}\ n<n 0≤a mod n<n。
如果 a m o d n = b m o d n a\ {\rm mod}\ n=b\ {\rm mod}\ n a mod n=b mod n,则说明 a a a与 b b b除以 n n n的余数相同,记为 a ≡ b ( m o d n ) a≡b({\rm mod}\ n) a≡b(mod n),并称模 n n n时 a a a等价于 b b b。模运算具有以下性质:
a ≡ b ( m o d n ) ⇔ n 是 b − a 的 一 个 因 子 a≡b({\rm mod}\ n)\ \ \ \ \ ⇔\ \ \ \ \ n是b-a的一个因子 a≡b(mod n) ⇔ n是b−a的一个因子
3. 多项式
给定一个非负整数 d d d, n n n的 d d d次多项式为
p ( n ) = a 0 + a 1 n + a 2 n 2 + ⋯ + a d n d = ∑ i = 0 d a i n i p(n)=a_0+a_1 n+a_2 n^2+⋯+a_d n^d=∑_{i=0}^da_i n^i p(n)=a0+a1n+a2n2+⋯+adnd=∑i=0daini
其中,常量 a 0 , a 1 , … , a d a_0, a_1, …, a_d a0,a1,…,ad是多项式的系数,并且 a d ≠ 0 a_d ≠ 0 ad̸=0。
一个多项式为渐近正当且仅当 a d > 0 a_d > 0 ad>0。对于一个 d d d次渐近正的多项式 p ( n ) p(n) p(n),有 p ( n ) = Θ ( n d ) p(n) = Θ(n^d) p(n)=Θ(nd)。如果一个函数 f ( n ) = O ( n d ) f(n) = O(n^d) f(n)=O(nd),则称该函数是多项式有界的。
4. 指数函数
(1) 指数函数的基本性质
对所有实数 a > 0 a > 0 a>0、 m m m和 n n n,以下等式成立
a 0 = 1 a^0=1 a0=1
a 1 = a a^1=a a1=a
a − 1 = 1 a a^{-1}=\frac{1}{a} a−1=a1
( a m ) n = a m n (a^m )^n=a^{mn} (am)n=amn
a m ∙ a n = a m + n a^m∙a^n=a^{m+n} am∙an=am+n
(2) 指数函数与多项式函数比较
给定一个指数函数 f ( n ) = a n f(n) = a^n f(n)=an (其中 a > 1 a > 1 a>1),一个多项式函数 g ( n ) = n b g(n) = n^b g(n)=nb,有 l i m n → ∞ n b a n = 0 lim_{n→∞}\frac {n^b}{a^n}=0 limn→∞annb=0。据此可得, n b = o ( a n ) n^b = o(a^n) nb=o(an),这说明任意底大于 1 1 1的指数函数比任意多项式函数增长得快。
(3) 自然对数的底 e e e
自然对数的底 e = 2.71828 … e = 2.71828… e=2.71828…。对所有实数 x x x,有
e x = 1 + x + x 2 2 ! + x 3 3 ! + ⋯ = ∑ i = 0 ∞ x i i ! e^x=1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+⋯=∑_{i=0}^∞\frac{x^i}{i!} ex=1+x+2!x2+3!x3+⋯=∑i=0∞i!xi
对所有实数 x x x,有 e x ≥ 1 + x e^x≥1+x ex≥1+x成立。只有当 x = 0 x = 0 x=0时,等号才成立。
当 ∣ x ∣ ≤ 1 |x|≤1 ∣x∣≤1时,可通过不等式 1 + x ≤ e x ≤ 1 + x + x 2 1+x≤e^x≤1+x+x^2 1+x≤ex≤1+x+x2来近似估计 e x e^x ex的值。当 x → 0 x→0 x→0时,用 1 + x 1+x 1+x来估计 e x e^x ex的近似值是足够精确的。
对所有实数 x x x,有 l i m n → ∞ ( 1 + x n ) n = e x lim_{n→∞}(1+\frac{x}{n})^n=e^x limn→∞(1+nx)n=ex。
5. 对数函数
本书约定下面的记号:
l g n = l o g 2 n ( 以 2 为 底 的 对 数 ) {\rm lg}\ n={\rm log}_2n\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (以2为底的对数) lg n=log2n (以2为底的对数)
l n n = l o g e n ( 自 然 对 数 ) {\rm ln}\ n={\rm log}_e n\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (自然对数) ln n=logen (自然对数)
l g k n = ( l g n ) k ( 对 数 的 幂 ) {\rm lg}^k n=({\rm lg}\ n)^k\ \ \ \ \ \ \ \ \ \ \ \ (对数的幂) lgkn=(lg n)k (对数的幂)
l g l g n = l g ( l g n ) ( 复 合 对 数 ) {\rm lg\ lg}\ n={\rm lg}({\rm lg}\ n)\ \ \ \ \ \ \ (复合对数) lg lg n=lg(lg n) (复合对数)
(1) 对数函数基本性质
对所有实数 a > 0 a > 0 a>0、 b > 0 b > 0 b>0、 c > 0 c > 0 c>0和 n n n,以下等式成立
a = b l o g b a a=b^{{\rm log}_ba} a=blogba
l o g c ( a b ) = l o g c a + l o g c b {\rm log}_c(ab)={\rm log}_c a+{\rm log}_c b logc(ab)=logca+logcb
l o g b a n = n l o g b a {\rm log}_ba^n=n{\rm log}_ba logban=nlogba
l o g b a = ( l o g c a ) / ( l o g c b ) {\rm log}_ba=({\rm log}_ca)/({\rm log}_cb) logba=(logca)/(logcb)
l o g b ( 1 / a ) = − l o g b a {\rm log}_b(1/a)=-{\rm log}_ba logb(1/a)=−logba
l o g b a = 1 l o g a b {\rm log}_ba=\frac{1}{{\rm log}_ab} logba=logab1
a l o g b c = c l o g b a a^{{\rm log}_bc}=c^{{\rm log}_ba} alogbc=clogba
(2) 当 ∣ x ∣ < 1 |x|<1 ∣x∣<1时, l n ( 1 + x ) {\rm ln}(1+x) ln(1+x)有级数展开
l n ( 1 + x ) = x − x 2 2 + x 3 3 − x 4 4 + x 5 5 − ⋯ {\rm ln}(1+x)=x-\frac{x^2}{2}+\frac{x^3}{3}-\frac{x^4}{4}+\frac{x^5}{5}-⋯ ln(1+x)=x−2x2+3x3−4x4+5x5−⋯
(3) 对于 x > − 1 x > -1 x>−1,还有以下不等式
x 1 + x ≤ l n ( 1 + x ) ≤ x \frac{x}{1+x}≤{\rm ln}(1+x)≤x 1+xx≤ln(1+x)≤x
(4) 如果对某个常量 k k k,有 f ( n ) = O ( l g k n ) f(n)=O({\rm lg}^kn) f(n)=O(lgkn),则称函数 f ( n ) f(n) f(n)是多对数有界的。
(5) 多对数函数与多项式函数比较
给定一个多对数函数 f ( n ) = l g b n f(n) = {\rm lg}^bn f(n)=lgbn,一个多项式函数 g ( n ) = n a g(n) = n^a g(n)=na (其中 a > 0 a > 0 a>0),有 l i m n → ∞ l g b n n a = 0 lim_{n→∞}\frac{{\rm lg}^bn}{n^a}=0 limn→∞nalgbn=0。据此可得, l g b n = o ( n a ) {\rm lg}^bn = o(n^a) lgbn=o(na),这说明任意渐近正的多项式函数都比任意多对数函数增长要快。
6. 阶乘
(1) 斯特林公式
![]()
(2) 以下渐近表达式成立
n ! = o ( n n ) n!=o(n^n) n!=o(nn)
n ! = ω ( 2 n ) n!=ω(2^n) n!=ω(2n)
l g ( n ! ) = Θ ( n l g n ) {\rm lg}(n!)=Θ(n{\rm lg}n) lg(n!)=Θ(nlgn)
(3) 对所有 n ≥ 1 n ≥ 1 n≥1,以下等式也成立
![]()
其中, 1 12 n + 1 < α n < 1 12 n \frac{1}{12n+1}<α_n<\frac{1}{12n} 12n+11<αn<12n1。
7. 多重函数
用记号 f ( i ) ( n ) f^{(i)}(n) f(i)(n)表示函数 f ( n ) f(n) f(n)重复 i i i次作用于一个初值 n n n上。 f ( i ) ( n ) f^{(i)}(n) f(i)(n)可以按照如下方式递归地定义。
![]()
例如,若 f ( n ) = 2 n f(n)=2n f(n)=2n,则 f ( i ) ( n ) = 2 i n f^{(i)}(n)=2^i n f(i)(n)=2in。
8. 多重对数函数
定义多重对数函数如下:
l g ∗ n = m i n { i ≥ 0 : l g ( i ) n ≤ 1 } {\rm lg}^* n=min\{i≥0: {\rm lg}^{(i)}n≤1\} lg∗n=min{i≥0:lg(i)n≤1}
多重对数函数的意义是:对一个初值 n n n最多可以连续应用多少次对数函数,才能使得最后结果小于或等于 1 1 1。对初值 n n n最多应用了对数函数的次数,就是多重对数函数的输出。
多重对数函数是一个增长极其缓慢的函数。
l g ∗ 2 = 1 {\rm lg}^*2=1 lg∗2=1
l g ∗ 4 = 2 {\rm lg}^*4=2 lg∗4=2
l g ∗ 16 = 3 {\rm lg}^*16=3 lg∗16=3
l g ∗ 65536 = 4 {\rm lg}^*65536=4 lg∗65536=4
l g ∗ ( 2 65536 ) = 5 {\rm lg}^*(2^{65536})=5 lg∗(265536)=5
9. 斐波那契数
斐波那契数 F ( n ) F(n) F(n)按照以下递归式来定义:
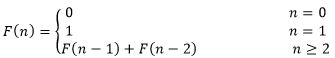
斐波那契数与黄金分割率 φ φ φ及其共轭数 φ ^ \hat{φ} φ^有关。 φ φ φ和 φ ^ \hat{φ} φ^是一元二次方程 x 2 = x + 1 x^2 = x+1 x2=x+1的根,它们的值为
φ = ( 1 + 5 ) / 2 = 1.61803 ⋯ φ=(1+\sqrt{5})/2=1.61803⋯ φ=(1+5)/2=1.61803⋯
φ ^ = ( 1 − 5 ) / 2 = − 0.61803 ⋯ \hat{φ}=(1-\sqrt{5})/2=-0.61803⋯ φ^=(1−5)/2=−0.61803⋯
斐波那契数与 φ φ φ和 φ ^ \hat{φ} φ^的关系如下:
![]()
也就是说斐波那契数 F ( n ) F(n) F(n)等于 φ n / 5 φ^n/\sqrt{5} φn/5舍入到最近的整数。因此,斐波那契数以指数形式增长。
练习
3.2-1 证明:若 f ( n ) f(n) f(n)和 g ( n ) g(n) g(n)是单调递增的函数,则函数 f ( n ) + g ( n ) f(n)+g(n) f(n)+g(n)和 f ( g ( n ) ) f(g(n)) f(g(n))也是单调递增的,此外,若 f ( n ) f(n) f(n)和 g ( n ) g(n) g(n)是非负的,则 f ( n ) • g ( n ) f(n)•g(n) f(n)•g(n)是单调递增的。
略
3.2-2 证明等式(3.16)。
a l o g b c = c l o g b a ( 3.16 ) a^{{\rm log}_bc}=c^{{\rm log}_ba}\ \ \ \ \ \ \ \ \ \ \ \ (3.16) alogbc=clogba (3.16)
解
对等式两边取对数。
左边: l o g b ( a l o g b c ) = l o g b a ∙ l o g b c {\rm log}_b(a^{{\rm log}_bc})={\rm log}_ba∙{\rm log}_bc logb(alogbc)=logba∙logbc
右边: l o g b ( c l o g b a ) = l o g b a ∙ l o g b c {\rm log}_b(c^{{\rm log}_ba})={\rm log}_ba∙{\rm log}_bc logb(clogba)=logba∙logbc
可以看到,取对数后,等式两边完全相等。故 a l o g b c = c l o g b a a^{{\rm log}_bc}=c^{{\rm log}_b a} alogbc=clogba成立。
3.2-3 证明等式(3.19)。并证明 n ! = ω ( 2 n ) 且 n ! = o ( n n ) n!=ω(2^n )且n!=o(n^n ) n!=ω(2n)且n!=o(nn)。
l g ( n ! ) = Θ ( n l g n ) ( 3.19 ) {\rm lg}(n!)=Θ(n{\rm lg}n)\ \ \ \ \ \ \ \ \ \ \ \ (3.19) lg(n!)=Θ(nlgn) (3.19)
解
(1) 证明 l g ( n ! ) = Θ ( n l g n ) {\rm lg}(n!)=Θ(n{\rm lg}n) lg(n!)=Θ(nlgn)
利用斯特林公式,可以得到
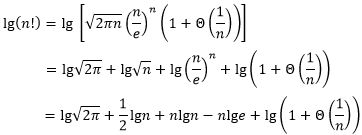
上式中,高阶项为 n l g n nlgn nlgn,忽略其他低阶项,可得 l g ( n ! ) = Θ ( n l g n ) {\rm lg}(n!)=Θ(n{\rm lg}n) lg(n!)=Θ(nlgn)。
(2) 证明 n ! = ω ( 2 n ) n!=ω(2^n) n!=ω(2n)
仍然采用斯特林公式。
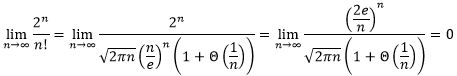
故 n ! = ω ( 2 n ) n!=ω(2^n ) n!=ω(2n)成立。
(3) 证明 n ! = o ( n n ) n!=o(n^n) n!=o(nn)
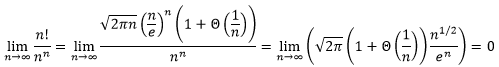
故 n ! = o ( n n ) n!=o(n^n ) n!=o(nn)成立。补充一下,上式的极限等于 0 0 0,是因为 “ “ “任意底大于 1 1 1的指数函数比任意多项式函数增长得快 ” ” ”,多项式函数 n 1 / 2 n^{1/2} n1/2是分子,而指数函数 e n e^n en是分母。
3.2-4 函数 ⌈ l g n ⌉ ! ⌈{\rm lg}n⌉! ⌈lgn⌉!多项式有界吗?函数 ⌈ l g l g n ⌉ ! ⌈{\rm lg lg}n⌉! ⌈lglgn⌉!多项式有界吗?
解
对于题目中的 2 2 2个函数,要直接判断它们是否多项式有界很困难。我们不妨考察任意一个多项式有界的函数 f ( n ) f(n) f(n),即 f ( n ) = O ( n k ) f(n) = O(n^k) f(n)=O(nk),其中 k k k为一个大于 0 0 0的常量。根据 O O O记号的定义,存在正常量 n 0 n_0 n0和 c c c,使得对所有 n ≥ n 0 n ≥ n_0 n≥n0,有
f ( n ) ≤ c n k f(n)≤cn^k f(n)≤cnk
对这个不等式两边取对数,得到
l g ( f ( n ) ) ≤ l g ( c n k ) = l g c + k l g n {\rm lg}(f(n))≤{\rm lg}(cn^k )={\rm lg}c+k{\rm lg}n lg(f(n))≤lg(cnk)=lgc+klgn。
可以取一个足够大的常量 c ′ c' c′,就可使得 l g c + k l g n ≤ c ′ l g n {\rm lg}c+k{\rm lg}n≤c'{\rm lg}n lgc+klgn≤c′lgn对所有 n ≥ n 0 n ≥ n_0 n≥n0成立,即 l g ( f ( n ) ) ≤ c ′ l g n {\rm lg}(f(n))≤c'{\rm lg}n lg(f(n))≤c′lgn对所有 n ≥ n 0 n ≥ n_0 n≥n0成立。由此可得 l g ( f ( n ) ) = O ( l g n ) {\rm lg}(f(n))=O({\rm lg}n) lg(f(n))=O(lgn)。
根据以上分析,可以得出以下推论。即如果一个函数 f ( n ) f(n) f(n)多项式有界,那么 f ( n ) f(n) f(n)的对数一定有渐近上界 O ( l g n ) O({\rm lg}n) O(lgn)。
f ( n ) = O ( n k ) ⇒ l g ( f ( n ) ) = O ( l g n ) f(n)=O(n^k)\ \ \ \ \ ⇒\ \ \ \ \ {\rm lg}(f(n))=O({\rm lg}n) f(n)=O(nk) ⇒ lg(f(n))=O(lgn)
那么上述推论反过来成不成立呢?即由 l g ( f ( n ) ) = O ( l g n ) {\rm lg}(f(n))=O({\rm lg}n) lg(f(n))=O(lgn),是否可以得出 f ( n ) = O ( n k ) f(n)=O(n^k) f(n)=O(nk)?
根据 l g ( f ( n ) ) = O ( l g n ) {\rm lg}(f(n))=O({\rm lg}n) lg(f(n))=O(lgn),存在正常量 n 0 n_0 n0和 k k k,使得对所有 n ≥ n 0 n ≥ n_0 n≥n0,有 l g ( f ( n ) ) ≤ k ∙ l g n = l g n k {\rm lg}(f(n))≤k∙{\rm lg}n={\rm lg}n^k lg(f(n))≤k∙lgn=lgnk。由此可得 f ( n ) ≤ n k f(n)≤n^k f(n)≤nk对所有 n ≥ n 0 n ≥ n_0 n≥n0都成立,这说明 f ( n ) = O ( n k ) f(n)=O(n^k) f(n)=O(nk)。于是下面的推论也成立。
l g ( f ( n ) ) = O ( l g n ) ⇒ f ( n ) = O ( n k ) {\rm lg}(f(n))=O({\rm lg}n)\ \ \ \ \ ⇒\ \ \ \ \ f(n)=O(n^k) lg(f(n))=O(lgn) ⇒ f(n)=O(nk)
综合以上分析, f ( n ) = O ( n k ) f(n)=O(n^k ) f(n)=O(nk)和 l g ( f ( n ) ) = O ( l g n ) {\rm lg}(f(n))=O({\rm lg}n) lg(f(n))=O(lgn)是等价的,即
f ( n ) = O ( n k ) ⇔ l g ( f ( n ) ) = O ( l g n ) f(n)=O(n^k )\ \ \ \ \ ⇔\ \ \ \ \ {\rm lg}(f(n))=O({\rm lg}n) f(n)=O(nk) ⇔ lg(f(n))=O(lgn)
下面我们用这个结论来判断函数 f 1 ( n ) = ⌈ l g n ⌉ ! f_1 (n)=⌈{\rm lg}n⌉! f1(n)=⌈lgn⌉!和 f 2 ( n ) = ⌈ l g l g n ⌉ ! f_2 (n)=⌈{\rm lg lg}n⌉! f2(n)=⌈lglgn⌉!是否多项式有界。
(1) f 1 ( n ) = ⌈ l g n ⌉ ! f_1 (n)=⌈{\rm lg}n⌉! f1(n)=⌈lgn⌉!
对函数 f 1 ( n ) f_1 (n) f1(n)取对数, l g ( f 1 ( n ) ) = l g ( ⌈ l g n ⌉ ! ) {\rm lg}(f_1 (n))={\rm lg}(⌈{\rm lg}n⌉!) lg(f1(n))=lg(⌈lgn⌉!)。根据3.2节的结论 l g ( n ! ) = Θ ( n l g n ) {\rm lg}(n!)=Θ(n{\rm lg}n) lg(n!)=Θ(nlgn),我们可以得到
l g ( ⌈ l g n ⌉ ! ) = Θ ( ⌈ l g n ⌉ ∙ l g ( ⌈ l g n ⌉ ) ) = Θ ( l g n ∙ l g l g n ) {\rm lg}(⌈{\rm lg}n⌉!)=Θ(⌈{\rm lg}n⌉∙{\rm lg}(⌈{\rm lg}n⌉))=Θ({\rm lg}n∙{\rm lg lg}n) lg(⌈lgn⌉!)=Θ(⌈lgn⌉∙lg(⌈lgn⌉))=Θ(lgn∙lglgn)
显然 Θ ( l g n ∙ l g l g n ) Θ({\rm lg}n∙{\rm lg lg}n) Θ(lgn∙lglgn)比 Θ ( l g n ) Θ({\rm lg}n) Θ(lgn)增长要快,所以 O ( l g n ) O({\rm lg}n) O(lgn)并不是 Θ ( l g n ∙ l g l g n ) Θ({\rm lg}n∙{\rm lg lg}n) Θ(lgn∙lglgn)的渐近上界,即 l g ( ⌈ l g n ⌉ ! ) ≠ O ( l g n ) {\rm lg}(⌈{\rm lg}n⌉!)≠O({\rm lg}n) lg(⌈lgn⌉!)̸=O(lgn)。根据上文的推论,有 ⌈ l g n ⌉ ! ≠ O ( n k ) ⌈{\rm lg}n⌉!≠O(n^k) ⌈lgn⌉!̸=O(nk),故 ⌈ l g n ⌉ ! ⌈{\rm lg}n⌉! ⌈lgn⌉!并不是多项式有界。
(2) f 2 ( n ) = ⌈ l g l g n ⌉ ! f_2 (n)=⌈{\rm lg lg}n⌉! f2(n)=⌈lglgn⌉!
对函数 f 2 ( n ) f_2 (n) f2(n)取对数, l g ( f 2 ( n ) ) = l g ( ⌈ l g l g n ⌉ ! ) {\rm lg}(f_2 (n))={\rm lg}(⌈{\rm lg lg}n⌉!) lg(f2(n))=lg(⌈lglgn⌉!)。同样根据3.2节的结论 l g ( n ! ) = Θ ( n l g n ) {\rm lg}(n!)=Θ(n{\rm lg}n) lg(n!)=Θ(nlgn),我们可以得到
l g ( ⌈ l g l g n ⌉ ! ) = Θ ( ⌈ l g l g n ⌉ ∙ l g ( ⌈ l g l g n ⌉ ) ) = Θ ( l g l g n ∙ l g l g l g n ) {\rm lg}(⌈{\rm lg lg}n⌉!)=Θ(⌈{\rm lg lg}n⌉∙{\rm lg}(⌈{\rm lg lg}n⌉))=Θ({\rm lg lg}n∙{\rm lg lg lg}n) lg(⌈lglgn⌉!)=Θ(⌈lglgn⌉∙lg(⌈lglgn⌉))=Θ(lglgn∙lglglgn)
这说明存在正常量 c c c和 n 0 n_0 n0,使得对所有 n ≥ n 0 n ≥ n_0 n≥n0,有 l g ( ⌈ l g l g n ⌉ ! ) ≤ c ∙ l g l g n ∙ l g l g l g n {\rm lg}(⌈{\rm lg lg}n⌉!)≤c∙{\rm lg lg}n∙{\rm lg lg lg}n lg(⌈lglgn⌉!)≤c∙lglgn∙lglglgn。因为 l g l g l g n ≤ l g l g n {\rm lg lg lg}n≤{\rm lg lg}n lglglgn≤lglgn,所以又有 l g ( ⌈ l g l g n ⌉ ! ) ≤ c ∙ ( l g l g n ) 2 {\rm lg}(⌈{\rm lg lg}n⌉!)≤c∙({\rm lg lg}n)^2 lg(⌈lglgn⌉!)≤c∙(lglgn)2。我们令 m = l g n m={\rm lg}n m=lgn,有 l g ( ⌈ l g l g n ⌉ ! ) ≤ c ∙ l g 2 m {\rm lg}(⌈{\rm lg lg}n⌉!)≤c∙{\rm lg}^2 m lg(⌈lglgn⌉!)≤c∙lg2m。利用3.2节的另一个结论 “ “ “任意多项式函数都比任意多对数函数增长要快 ” ” ”,我们有
l g ( ⌈ l g l g n ⌉ ! ) ≤ c ∙ l g 2 m = O ( m ) = O ( l g n ) {\rm lg}(⌈{\rm lg lg}n⌉!)≤c∙{\rm lg}^2 m=O(m)=O({\rm lg}n) lg(⌈lglgn⌉!)≤c∙lg2m=O(m)=O(lgn)。
根据上文的推论,有 ⌈ l g l g n ⌉ ! = O ( n k ) ⌈{\rm lg lg}n⌉!=O(n^k ) ⌈lglgn⌉!=O(nk),即 ⌈ l g l g n ⌉ ! ⌈{\rm lg lg}n⌉! ⌈lglgn⌉!是多项式有界的。
3.2-5 如下两个函数中,哪一个渐近更大些: l g ( l g ∗ n ) {\rm lg}({\rm lg}^*n) lg(lg∗n)还是 l g ∗ ( l g n ) {\rm lg}^* ({\rm lg}n) lg∗(lgn)?
解
先分析 l g ∗ ( l g n ) {\rm lg}^* ({\rm lg}n) lg∗(lgn)。 l g ∗ {\rm lg}^* lg∗的定义是连续应用对数函数的次数,由于 l g n {\rm lg}n lgn已经对 n n n应用了一次对数函数,故对 l g n {\rm lg}n lgn应用 l g ∗ {\rm lg}^* lg∗,应当比对 n n n应用 l g ∗ {\rm lg}^* lg∗要小 1 1 1,即 l g ∗ ( l g n ) = l g ∗ n − 1 {\rm lg}^* ({\rm lg}n)={\rm lg}^* n-1 lg∗(lgn)=lg∗n−1。
令 m = l g ∗ n m={\rm lg}^* n m=lg∗n,那么 l g ∗ ( l g n ) = l g ∗ n − 1 = m − 1 {\rm lg}^* ({\rm lg}n)={\rm lg}^* n-1=m-1 lg∗(lgn)=lg∗n−1=m−1,并且 l g ( l g ∗ n ) = l g m {\rm lg}({\rm lg}^* n)={\rm lg}m lg(lg∗n)=lgm。利用3.2节的结论 “ “ “任意多项式函数都比任意多对数函数增长要快 ” ” ”,可以得出 m − 1 m-1 m−1比 l g m {\rm lg}m lgm增长要快,这说明 l g ∗ ( l g n ) {\rm lg}^* ({\rm lg}n) lg∗(lgn)比 l g ( l g ∗ n ) {\rm lg} ({\rm lg^*}n) lg(lg∗n)渐近更大。
3.2-6 证明:黄金分割率 φ φ φ及其共轭数 φ ^ \hat{φ} φ^都满足方程 x 2 = x + 1 x^2 = x + 1 x2=x+1。
略
3.2-7 用归纳法证明:第 i i i个斐波那契数满足等式
![]()
其中, φ φ φ是黄金分割率且 φ ^ \hat{φ} φ^是其共轭数。
解
先考虑初始情况 i = 0 i = 0 i=0和 i = 1 i = 1 i=1。
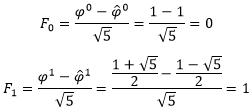
故 F i = φ i − φ ^ i 5 F_i=\frac{φ^i-\hat{φ}^i}{\sqrt{5}} Fi=5φi−φ^i对初始情况 i = 0 i = 0 i=0和 i = 1 i = 1 i=1成立。
现在假设等式对 0 , 1 , … , i − 1 0, 1, …, i-1 0,1,…,i−1都成立,于是有
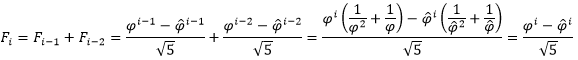
综上所述, F i = φ i − φ ^ i 5 F_i=\frac{φ^i-\hat{φ}^i}{\sqrt{5}} Fi=5φi−φ^i对所有 i ≥ 0 i ≥ 0 i≥0的整数都成立。
3.2-8 证明: k l n k = Θ ( n ) k{\rm ln}k=Θ(n) klnk=Θ(n)蕴含着 k = Θ ( n / l n n ) k=Θ(n/{\rm ln}n) k=Θ(n/lnn)。
解
k l n k = Θ ( n ) k{\rm ln}k=Θ(n) klnk=Θ(n)意味着存在正常量 c 1 c_1 c1、 c 2 c_2 c2和 n 0 n_0 n0,使得当 n ≥ n 0 n ≥ n_0 n≥n0时,有
![]()
对这个不等式取以e为底的指数,得到
![]()
即
![]()
(1) 首先证明当 n n n足够大时,有 k < n k < n k<n
注意,这里的 k k k应当理解为一个自变量为 n n n的函数,而不是一个常数。采用反证法,假设存在 k ≥ n k ≥ n k≥n。由于 e c 2 e^{c_2} ec2是常数,当 n n n足够大时,一定会有 n > e c 2 n>e^{c_2} n>ec2。我们已经假设存在 k ≥ n k ≥ n k≥n,于是有 e k + k ≥ e n + n > e n + e c 2 e^k+k≥e^n+n>e^n+e^{c_2} ek+k≥en+n>en+ec2,这与上面的不等式 e k + k ≤ e c 2 + e n e^k+k≤e^{c_2 }+e^n ek+k≤ec2+en矛盾,所以假设不成立,故当 n n n足够大时,一定有 k < n k < n k<n。
(2) 证明 k = Ω ( n / l n n ) k=Ω(n/{\rm ln}n) k=Ω(n/lnn)
现在利用(1)的结论来证明 k = Ω ( n / l n n ) k=Ω(n/{\rm ln}n) k=Ω(n/lnn)。根据不等式①,当 n n n足够大时,有 c 1 n ≤ k l n k c_1 n≤k{\rm ln}k c1n≤klnk。根据(1)的结论,当 n n n足够大时,有 k < n k < n k<n。所以当 n n n足够大时,有
![]()
故 k = Ω ( n / l n n ) k=Ω(n/{\rm ln}n) k=Ω(n/lnn)成立。
(2) 证明 k = O ( n / l n n ) k=O(n/{\rm ln}n) k=O(n/lnn)
以下分析都建立在 n n n足够大的前提下。将不等式①写为一个不等式组
![]()
将不等式④两边取对数,得到
![]()
即
![]()
将不等式⑤和⑥左边两边分别相乘得到
![]()
即
![]()
因为 l n l n k < l n k {\rm lnln}k< {\rm ln}k lnlnk<lnk,所以有 l n l n k l n k < 1 \frac {{\rm lnln}k}{{\rm ln}k}<1 lnklnlnk<1。而 l n c 1 l n k > 0 \frac{{\rm ln}c_1}{{\rm ln}k}>0 lnklnc1>0显然成立。所以有
![]()
将不等式⑧代入不等式⑦中,可以得到
![]()
由此可见,当 n n n足够大时,有 k < 2 c 2 n / l n n k<2c_2n/{\rm ln}n k<2c2n/lnn。故 k = O ( n / l n n ) k=O(n/{\rm ln}n) k=O(n/lnn)成立。
综上所述, k l n k = Θ ( n ) k{\rm ln}k=Θ(n) klnk=Θ(n)意味着 k = Θ ( n / l n n ) k=Θ(n/{\rm ln}n) k=Θ(n/lnn)。