数据结构:图的基本概念
数据结构:图的基本概念
- 一、什么是图?
- 二、图的分类
-
- 1. 无向图
-
- 1.1 无向完全图
- 1.2 连通图(无向图)
- 1.3 无向图的度
- 2. 有向图
-
- 2.1 有向完全图
- 2.2 强连通图(有向图)
- 2.3 有向图的度
- 2. 稀疏图和稠密图
- 3. 有环图和无环图
- 4. 加权图和无权图
- 三、图的存储结构
-
- 1. 邻接矩阵
- 2. 邻接表
- 参考链接
一、什么是图?
图是一种非线性的数据结构,表示多对多的关系。
图(Graph)是由顶点的有穷非空集合和顶点之间边的集合组成,通常表示为:G(V, E),其中,G表示一个图,V是图G中顶点的集合,E是图G中边的集合。
在图中需要注意的是:
- 线性表和树可以看做特殊的图。
- 线性表中我们把数据元素叫元素,树中将数据元素叫结点,在图中数据元素,我们则称之为顶点(Vertex)
- 线性表可以没有元素,称为空表;树中可以没有节点,称为空树;但是,在图中不允许没有顶点(有穷非空性)
- 线性表中的各元素是线性关系,树中的各元素是层次关系,而图中各顶点的关系是用边来表示(边集可以为空)。
二、图的分类
1. 无向图
顾名思义,无向图就是图上的边没有方向。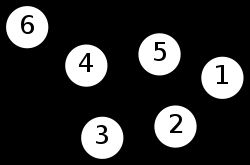 上图就是一个无向图。该图的顶点集为 V = { 1 , 2 , 3 , 4 , 5 , 6 } ,边集 E = { ( 1 , 2 ) , ( 1 , 5 ) , ( 2 , 3 ) , ( 2 , 5 ) , ( 3 , 4 ) , ( 4 , 5 ) , ( 4 , 6 ) }。在无向图中,边 ( u , v )和边 ( v , u )是一样的,也就是说和方向无关。
上图就是一个无向图。该图的顶点集为 V = { 1 , 2 , 3 , 4 , 5 , 6 } ,边集 E = { ( 1 , 2 ) , ( 1 , 5 ) , ( 2 , 3 ) , ( 2 , 5 ) , ( 3 , 4 ) , ( 4 , 5 ) , ( 4 , 6 ) }。在无向图中,边 ( u , v )和边 ( v , u )是一样的,也就是说和方向无关。
1.1 无向完全图
在无向图中,如果任意两个顶点之间都存在边,则称该图为无向完全图。有n个顶点的无向完全图有n(n-1)/2 条边。
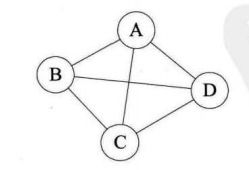
1.2 连通图(无向图)
在无向图G中,如果从顶点u到顶点v有路径,则称u和v是连通的。
如果对于图中任意两个顶点u、v,都有(u, v)∈E(即u和v都是连通的),则称G是连通图。
无向图中的极大连通子图称为连通分量。
连通分量需要满足:
- 必须是子图;
- 必须是连通的;
- 含有极大顶点数;
- 包含依附于这些顶点的所有边。
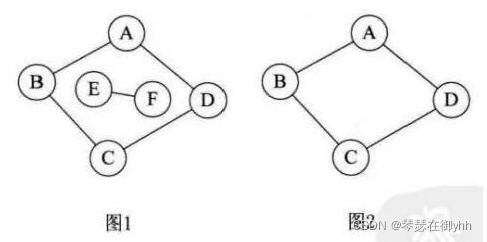

上图中,图1是无向非连通图(因为A与E不连通,即不满足图上任意两个顶点连通),但是有两个连通分量,即图2和图3。而图4,尽管是图1的子图,但是它却不满足连通子图的极大顶点数(图2满足)。 因此它不是图1的无向图的连通分量。
这里,补充一个概念。
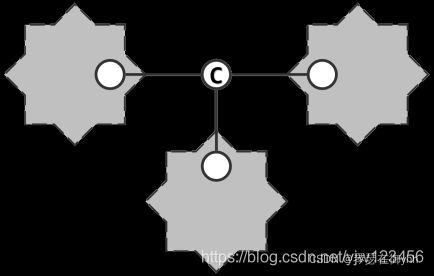
关节点(割点):某些特定的顶点对于保持图或连通分支的连通性有特殊的重要意义。如果移除某个顶点将使图或者分支失去连通性,则称该顶点为关节点。如下图中的 顶点c 。
1.3 无向图的度
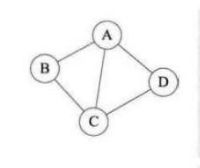
对于无向图G= (V, E), 如果边(v,v’)属于E, 则称顶点v和v‘互为邻接点,即(v,v’)与顶点v和v’相关联。顶点v的度是和v相关联的边的数目。如下面这个无向图,顶点A 的度为3。各个顶点度的和=3+2+3+2=10。而此图的边数是5,推敲后发现,边数其实就是各顶点度数和的一半,多出的一半是因为重复两次计数。
2. 有向图
顾名思义,有向图就是图上的边有方向。
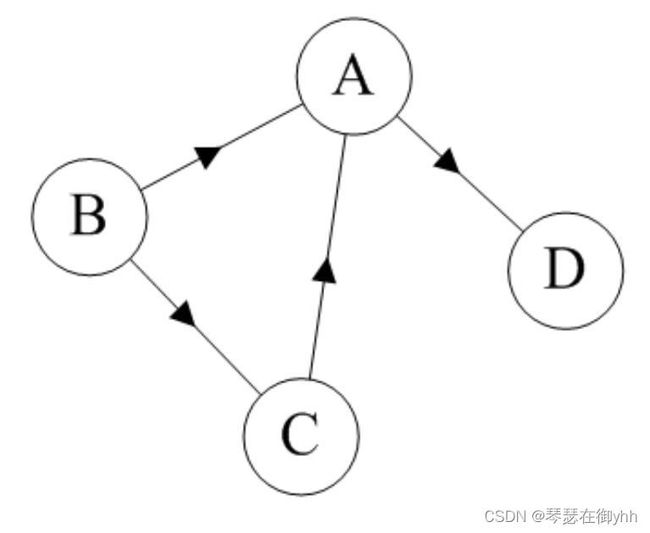 上图就是一个有向图。该图的顶点集为 V = { A , B , C , D } ,边集 E = { < B , A > , < B , C > , < C , A > , < A , D > }。在有向图中,边 < u , v >和边 < v , u >是不一样的。
上图就是一个有向图。该图的顶点集为 V = { A , B , C , D } ,边集 E = { < B , A > , < B , C > , < C , A > , < A , D > }。在有向图中,边 < u , v >和边 < v , u >是不一样的。
通常情况下,有向图中的边用< >表示,无向图中的边用( )表示。
2.1 有向完全图
在有向图中,如果任意两个顶点之间都存在方向互为相反的两条边,则称该图为有向完全图。n个顶点的有向完全图含有n*(n-1)条边。
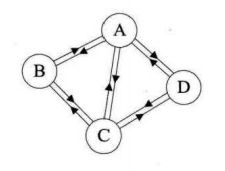
2.2 强连通图(有向图)
在有向图G中,如果对于每一对顶点vi、vj且vi≠vj,从vi到vj和从vj到vi都存在路径,则称G是强连通图。
有向图中的极大强连通子图称做有向图的强连通分量。
强连通图具有如下定理:一个有向图G是强连通的,当且仅当G中有一个回路,它至少包含每个节点一次。
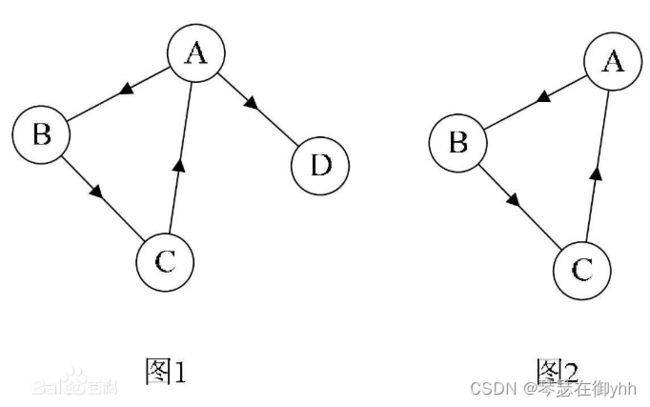 如上图所示,图1不是强连通图,图2是强连通图。图2也可以看做是图1的强连通分量。
如上图所示,图1不是强连通图,图2是强连通图。图2也可以看做是图1的强连通分量。
2.3 有向图的度
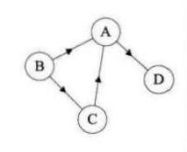
对于有向图G = (V, E),如果边
从顶点v出发的边的数目称为v的出度;到达顶点v的边的数目称为v的入度,顶点v的度=出度+入度。以下面这个有向图为例,
顶点A的入度是2 (从B到A的边,从C到A的边),出度是1(从A到D的边),所以顶点A的度为2+1=3。此有向图的边有4 条,而各顶点的出度和为1+2+1+0=4,各顶点的入度和=2+0+1+1=4。
2. 稀疏图和稠密图
按照边的多少来分稀疏图和稠密图。假设一个图的顶点数为n,如果边数大于n*log n,则该图为稠密图,反之则为稀疏图。
3. 有环图和无环图
先了解一些概念:
- 路径(path): 依次遍历顶点序列之间的边所形成的轨迹。注意,依次就意味着有序,先1后2和先2后1不一样。
- 简单路径: 没有重复顶点的路径称为简单路径。说白了,这一条路径中没有出现绕了一圈回到同一顶点的情况。
- 环: 包含相同的顶点两次或者两次以上。例如,下图中路径 < 1 , 2 , 4 , 3 , 1 >,其中1出现了两次,那么这条路径就是一个环路。

因此,顾名思义,有环图就是图上有环,无环图就是没有环的图。
特别地,有向无环图有,又叫做DAG(Directed Acyline Graph),具有一些很好的性质,很多动态规划的问题都可以转化成DAG中的最长路径、最短路径或者路径计数的问题。
4. 加权图和无权图
首先需要了解一下什么是权。有些图的边上具有与它相关的数字,这种与图的边相关的数叫做权(Weight)。这些权可以表示从一个顶点到另一个顶点的距离或耗费。因此加权图就是边上带有权重的图,与其对应的是无权图,或叫等权图,即边上没有权重信息。如果一张图不含权重信息,我们就认为边与边之间没有差别。
通常情况下,加权图会被称为网络。
三、图的存储结构
1. 邻接矩阵
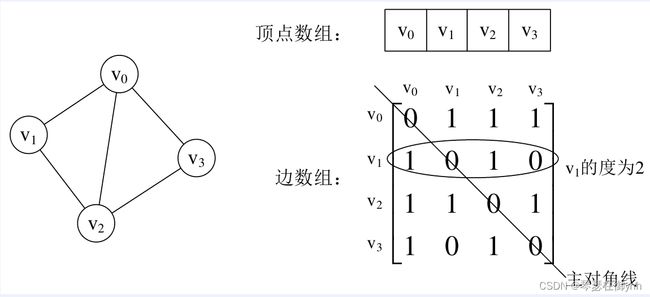
图的邻接矩阵(Adjacency Matrix)存储方式是用两个数组来表示图。一个一维数组存储图中顶点的信息,一个二维数组(称为邻接矩阵)存储图中边的信息。
(1)下图是使用邻接矩阵存储无向图。如图所示,设置两个数组,顶点数组为vertex[4] = {v0, v1, v2, v3},边数组arc[4][4]实际上是一个矩阵。对于矩阵的主对角线的值,即arc[0][0]、arc[1][1]、arc[2][2]、arc[3][3]全为0,这是因为顶点上不存在自环的边。通过这个例子可以看出,无向图的邻接矩阵是一个对称矩阵。
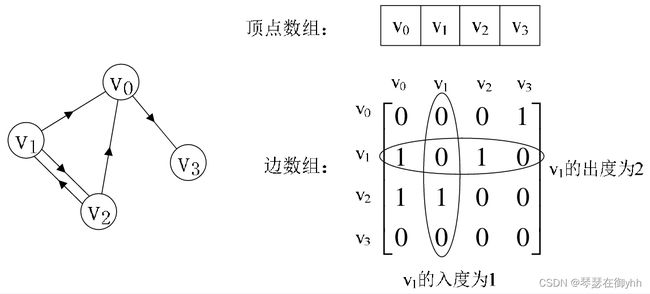
 (2)下图是使用邻接矩阵存储有向图。如图所示,设置两个数组,顶点数组为vertex[4] = {v0, v1, v2, v3},边数组arc[4][4]实际上是一个矩阵。对于矩阵的主对角线的值,即arc[0][0]、arc[1][1]、arc[2][2]、arc[3][3]全为0,这是因为顶点上不存在自环的边。通过这个例子可以看出,有向图的邻接矩阵并不是一个对称矩阵。
(2)下图是使用邻接矩阵存储有向图。如图所示,设置两个数组,顶点数组为vertex[4] = {v0, v1, v2, v3},边数组arc[4][4]实际上是一个矩阵。对于矩阵的主对角线的值,即arc[0][0]、arc[1][1]、arc[2][2]、arc[3][3]全为0,这是因为顶点上不存在自环的边。通过这个例子可以看出,有向图的邻接矩阵并不是一个对称矩阵。
2. 邻接表
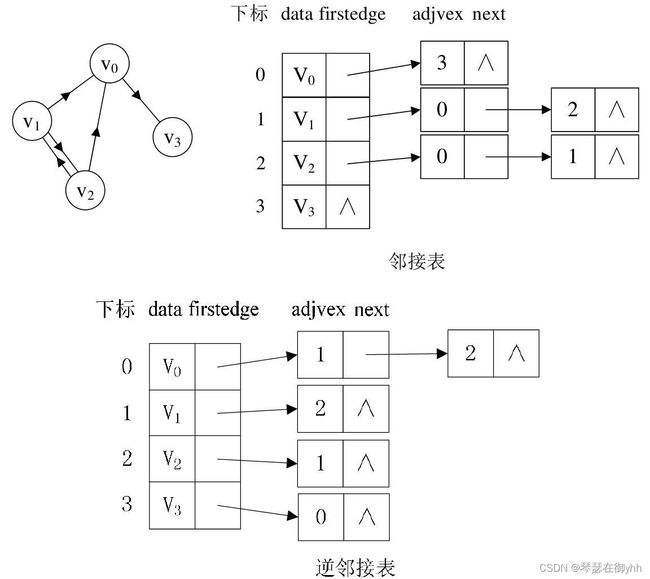
邻接表由表头节点和表节点两部分组成,图中每个顶点均对应一个存储在数组中的表头节点。如果这个表头节点所对应的顶点存在邻接节点,则把邻接节点依次存放于表头节点所指向的单向链表中。
(1)下图所示的就是一个无向图的邻接表结构。从该图可以看出,顶点表的各个结点由data和firstedge两个域表示,data是数据域,存储顶点的信息,firstedge是指针域,指向边表的第一个结点,即此顶点的第一个邻接点。边表结点由adjvex和next两个域组成。adjvex是邻接点域,存储某顶点的邻接点在顶点表中的下标,next则存储指向边表中下一个结点的指针。例如:v1顶点与v0、v2互为邻接点,则在v1的边表中,adjvex分别为v0的0和v2的2。

(2)下图是使用邻接表存储有向图。值得注意的是,由于有方向的,因此有向图的邻接表分为出边表和入边表(又称逆邻接表),出边表的表节点存放的是从表头节点出发的有向边所指的尾节点;入边表的表节点存放的则是指向表头节点的某个顶点。
显而易见,如果图是一个稀疏图,用邻接表进行存储比较合适,如果图是一个稠密图,则用邻接矩阵更合适。
参考链接
https://www.cnblogs.com/xiaobingqianrui/p/8902111.html
https://www.cnblogs.com/ssyfj/p/9474032.html
https://blog.csdn.net/yjw123456/article/details/90211563