机器学习之KNN算法:日撸Java三百行day51-53
一、什么是KNN算法
K近邻(K-Nearest Neighbor, KNN),是一种最简单和最经典的有监督学习算法之一。KNN算法是最简单的分类器,可以应用于分类和回归问题。同时,它也不具备任何显式的学习过程或训练过程,属于懒惰学习(Lazy Learning)。所谓懒惰学习,类似于开卷考试,在已有数据中去找答案。虽然KNN是懒惰学习,但它的算法效果十分出色。
二、KNN算法的基本思想
以iris分类问题为例:将iris的特征数据散布在特征空间中,将每一个分类对象抽象成一个点。找到距离它最近的K个邻居,并判断这些邻居属于什么类型的花。每个邻居进行投票,票数最高的花种即为该分类对象的花种。即:综合K个邻居的标签值作为新样本的预测值。
三、KNN算法的基本要素
1、K值的选择
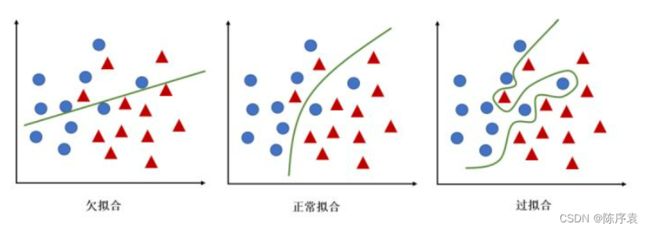
KNN算法中的K代表着邻居的个数。当K取值较小时,仅用较小领域的训练样本进行预测,训练误差会减小,决策结果紧跟着训练样本,泛化能力减弱;当K取值较大时,需要利用较大领域的训练样本进行预测,若训练集包含“噪声样本”,会影响算法决策结果,训练误差会增大,但泛化能力有一定的提高。同时,K值较小,模型拟合能力较强;K值较大,模型容易过拟合。
2、距离度量
由于特征空间中两个实例点之间的距离是二者相似程度的反映,因此KNN算法通过距离度量来找K个邻居。在实际应用中,我们往往需要根据应用的场景和数据本身的特点来选择距离计算方法。当已有的距离度量方法无法满足实际应用需求时,还需要有针对性地提出适合具体问题的距离度量方法。常用的距离度量方法有:曼哈顿距离、欧几里得距离。
•曼哈顿距离(Manhattan Distance)
曼哈顿距离,也被称为出租车几何,是一种用来度量多维维实数空间内两个样本点之间距离的方法。假设多维空间的维度为![]() ,
,![]() 和
和![]() 是两个样本点,则
是两个样本点,则![]() 和
和![]() 之间的曼哈顿距离计算公式为:
之间的曼哈顿距离计算公式为:
![]()
曼哈顿距离等于两个样本之间每一维度之差的绝对值之和。曼哈顿距离的含义可以对应到规划为方框建筑的城市(如曼哈顿),两个地点的出租车最短行驶距离。在使用曼哈顿距离时,也需要考虑变量之间取值范围不同对结果的影响。
•欧几里得距离(Euclidean Distance)
欧几里得距离,也称为欧式距离,是最常见的距离度量方式之一。该度量方法衡量的是多维空间中两个样本点之间的绝对距离。假设多维空间的维度为![]() ,
,![]() 和
和![]() 是两个样本点,则
是两个样本点,则![]() 和
和![]() 之间的欧式距离计算公式为:
之间的欧式距离计算公式为:
可见,欧氏距离由两个样本之间每一维度之差的平方和计算而来。当维度之间的取值范围差别太大时,欧氏距离容易被那些取值范围大的变量所主导,从而会大大降低模型的效果。因此在特定情况下需要对数据进行归一化或标准化处理。
3、决策方法
决策方法就计算确认到新实例样本最邻近的K个实例样本后,如何确定新实例样本的标签值。
•对于KNN分类:通常就是“多数表决,少数服从多数”,k个“邻居”的最多数所属类别为预测类别(可以基于距离的远近做加权,一般可以用距离的倒数作为权重,越近的邻居的类别更有可信度)。
•对于KNN回归:通常就是“取均值”,以k个“邻居”的标签值的平均值作为预测值(同理也可以基于距离的远近做加权)。
四、算法的基本流程及操作
以鸢尾花iris数据集处理实验为例,阐述KNN算法的基本流程。
①读入数据文件iris.arff,生成数据集。iris数据集是机器学习领域常用的一类数据集,共150个。下载地址在此。倘若下载不畅,可直接将下列内容拷贝另存为iris.arff文件。
@RELATION iris
@ATTRIBUTE sepallength REAL
@ATTRIBUTE sepalwidth REAL
@ATTRIBUTE petallength REAL
@ATTRIBUTE petalwidth REAL
@ATTRIBUTE class {Iris-setosa,Iris-versicolor,Iris-virginica}
@DATA
5.1,3.5,1.4,0.2,Iris-setosa
4.9,3.0,1.4,0.2,Iris-setosa
4.7,3.2,1.3,0.2,Iris-setosa
4.6,3.1,1.5,0.2,Iris-setosa
5.0,3.6,1.4,0.2,Iris-setosa
5.4,3.9,1.7,0.4,Iris-setosa
4.6,3.4,1.4,0.3,Iris-setosa
5.0,3.4,1.5,0.2,Iris-setosa
4.4,2.9,1.4,0.2,Iris-setosa
4.9,3.1,1.5,0.1,Iris-setosa
5.4,3.7,1.5,0.2,Iris-setosa
4.8,3.4,1.6,0.2,Iris-setosa
4.8,3.0,1.4,0.1,Iris-setosa
4.3,3.0,1.1,0.1,Iris-setosa
5.8,4.0,1.2,0.2,Iris-setosa
5.7,4.4,1.5,0.4,Iris-setosa
5.4,3.9,1.3,0.4,Iris-setosa
5.1,3.5,1.4,0.3,Iris-setosa
5.7,3.8,1.7,0.3,Iris-setosa
5.1,3.8,1.5,0.3,Iris-setosa
5.4,3.4,1.7,0.2,Iris-setosa
5.1,3.7,1.5,0.4,Iris-setosa
4.6,3.6,1.0,0.2,Iris-setosa
5.1,3.3,1.7,0.5,Iris-setosa
4.8,3.4,1.9,0.2,Iris-setosa
5.0,3.0,1.6,0.2,Iris-setosa
5.0,3.4,1.6,0.4,Iris-setosa
5.2,3.5,1.5,0.2,Iris-setosa
5.2,3.4,1.4,0.2,Iris-setosa
4.7,3.2,1.6,0.2,Iris-setosa
4.8,3.1,1.6,0.2,Iris-setosa
5.4,3.4,1.5,0.4,Iris-setosa
5.2,4.1,1.5,0.1,Iris-setosa
5.5,4.2,1.4,0.2,Iris-setosa
4.9,3.1,1.5,0.1,Iris-setosa
5.0,3.2,1.2,0.2,Iris-setosa
5.5,3.5,1.3,0.2,Iris-setosa
4.9,3.1,1.5,0.1,Iris-setosa
4.4,3.0,1.3,0.2,Iris-setosa
5.1,3.4,1.5,0.2,Iris-setosa
5.0,3.5,1.3,0.3,Iris-setosa
4.5,2.3,1.3,0.3,Iris-setosa
4.4,3.2,1.3,0.2,Iris-setosa
5.0,3.5,1.6,0.6,Iris-setosa
5.1,3.8,1.9,0.4,Iris-setosa
4.8,3.0,1.4,0.3,Iris-setosa
5.1,3.8,1.6,0.2,Iris-setosa
4.6,3.2,1.4,0.2,Iris-setosa
5.3,3.7,1.5,0.2,Iris-setosa
5.0,3.3,1.4,0.2,Iris-setosa
7.0,3.2,4.7,1.4,Iris-versicolor
6.4,3.2,4.5,1.5,Iris-versicolor
6.9,3.1,4.9,1.5,Iris-versicolor
5.5,2.3,4.0,1.3,Iris-versicolor
6.5,2.8,4.6,1.5,Iris-versicolor
5.7,2.8,4.5,1.3,Iris-versicolor
6.3,3.3,4.7,1.6,Iris-versicolor
4.9,2.4,3.3,1.0,Iris-versicolor
6.6,2.9,4.6,1.3,Iris-versicolor
5.2,2.7,3.9,1.4,Iris-versicolor
5.0,2.0,3.5,1.0,Iris-versicolor
5.9,3.0,4.2,1.5,Iris-versicolor
6.0,2.2,4.0,1.0,Iris-versicolor
6.1,2.9,4.7,1.4,Iris-versicolor
5.6,2.9,3.6,1.3,Iris-versicolor
6.7,3.1,4.4,1.4,Iris-versicolor
5.6,3.0,4.5,1.5,Iris-versicolor
5.8,2.7,4.1,1.0,Iris-versicolor
6.2,2.2,4.5,1.5,Iris-versicolor
5.6,2.5,3.9,1.1,Iris-versicolor
5.9,3.2,4.8,1.8,Iris-versicolor
6.1,2.8,4.0,1.3,Iris-versicolor
6.3,2.5,4.9,1.5,Iris-versicolor
6.1,2.8,4.7,1.2,Iris-versicolor
6.4,2.9,4.3,1.3,Iris-versicolor
6.6,3.0,4.4,1.4,Iris-versicolor
6.8,2.8,4.8,1.4,Iris-versicolor
6.7,3.0,5.0,1.7,Iris-versicolor
6.0,2.9,4.5,1.5,Iris-versicolor
5.7,2.6,3.5,1.0,Iris-versicolor
5.5,2.4,3.8,1.1,Iris-versicolor
5.5,2.4,3.7,1.0,Iris-versicolor
5.8,2.7,3.9,1.2,Iris-versicolor
6.0,2.7,5.1,1.6,Iris-versicolor
5.4,3.0,4.5,1.5,Iris-versicolor
6.0,3.4,4.5,1.6,Iris-versicolor
6.7,3.1,4.7,1.5,Iris-versicolor
6.3,2.3,4.4,1.3,Iris-versicolor
5.6,3.0,4.1,1.3,Iris-versicolor
5.5,2.5,4.0,1.3,Iris-versicolor
5.5,2.6,4.4,1.2,Iris-versicolor
6.1,3.0,4.6,1.4,Iris-versicolor
5.8,2.6,4.0,1.2,Iris-versicolor
5.0,2.3,3.3,1.0,Iris-versicolor
5.6,2.7,4.2,1.3,Iris-versicolor
5.7,3.0,4.2,1.2,Iris-versicolor
5.7,2.9,4.2,1.3,Iris-versicolor
6.2,2.9,4.3,1.3,Iris-versicolor
5.1,2.5,3.0,1.1,Iris-versicolor
5.7,2.8,4.1,1.3,Iris-versicolor
6.3,3.3,6.0,2.5,Iris-virginica
5.8,2.7,5.1,1.9,Iris-virginica
7.1,3.0,5.9,2.1,Iris-virginica
6.3,2.9,5.6,1.8,Iris-virginica
6.5,3.0,5.8,2.2,Iris-virginica
7.6,3.0,6.6,2.1,Iris-virginica
4.9,2.5,4.5,1.7,Iris-virginica
7.3,2.9,6.3,1.8,Iris-virginica
6.7,2.5,5.8,1.8,Iris-virginica
7.2,3.6,6.1,2.5,Iris-virginica
6.5,3.2,5.1,2.0,Iris-virginica
6.4,2.7,5.3,1.9,Iris-virginica
6.8,3.0,5.5,2.1,Iris-virginica
5.7,2.5,5.0,2.0,Iris-virginica
5.8,2.8,5.1,2.4,Iris-virginica
6.4,3.2,5.3,2.3,Iris-virginica
6.5,3.0,5.5,1.8,Iris-virginica
7.7,3.8,6.7,2.2,Iris-virginica
7.7,2.6,6.9,2.3,Iris-virginica
6.0,2.2,5.0,1.5,Iris-virginica
6.9,3.2,5.7,2.3,Iris-virginica
5.6,2.8,4.9,2.0,Iris-virginica
7.7,2.8,6.7,2.0,Iris-virginica
6.3,2.7,4.9,1.8,Iris-virginica
6.7,3.3,5.7,2.1,Iris-virginica
7.2,3.2,6.0,1.8,Iris-virginica
6.2,2.8,4.8,1.8,Iris-virginica
6.1,3.0,4.9,1.8,Iris-virginica
6.4,2.8,5.6,2.1,Iris-virginica
7.2,3.0,5.8,1.6,Iris-virginica
7.4,2.8,6.1,1.9,Iris-virginica
7.9,3.8,6.4,2.0,Iris-virginica
6.4,2.8,5.6,2.2,Iris-virginica
6.3,2.8,5.1,1.5,Iris-virginica
6.1,2.6,5.6,1.4,Iris-virginica
7.7,3.0,6.1,2.3,Iris-virginica
6.3,3.4,5.6,2.4,Iris-virginica
6.4,3.1,5.5,1.8,Iris-virginica
6.0,3.0,4.8,1.8,Iris-virginica
6.9,3.1,5.4,2.1,Iris-virginica
6.7,3.1,5.6,2.4,Iris-virginica
6.9,3.1,5.1,2.3,Iris-virginica
5.8,2.7,5.1,1.9,Iris-virginica
6.8,3.2,5.9,2.3,Iris-virginica
6.7,3.3,5.7,2.5,Iris-virginica
6.7,3.0,5.2,2.3,Iris-virginica
6.3,2.5,5.0,1.9,Iris-virginica
6.5,3.0,5.2,2.0,Iris-virginica
6.2,3.4,5.4,2.3,Iris-virginica
5.9,3.0,5.1,1.8,Iris-virginica
操作代码:
public KnnClassification(String paraFilename) {
try {
FileReader fileReader=new FileReader(paraFilename);
dataset=new Instances(fileReader);
dataset.setClassIndex(dataset.numAttributes()-1);
fileReader.close();
}catch (Exception ee) {
System.out.println("Error occurred while trying to read \'" + paraFilename
+ "\' in KnnClassification constructor.\r\n" + ee);
System.exit(0);
// TODO: handle exception
}
}
KnnClassification tempClassifier=new KnnClassification("D:/software/eclipse/eclipse-workspace/day51/iris.arff");②将数据集中数据序号打乱,即:随机初始化数据。如:[0,1,2,3]打乱为[3,2,0,1]。
操作代码:
public static int[] getRandomIndices(int paralength) {//获取随机指标/位置
int[] resultIndices=new int[paralength];
//第一步:初始化
for(int i=0;i③将数据集中数据划分为训练集与测试集,在本次实验中,80%的数据划分为训练集,20%的数据划分为测试集。
public void splitTrainingTesting(double paraTrainingFraction) {//该函数用于将数据集分为训练集与测试集
int tempSize=dataset.numInstances();//获取数据集大小
int[] tempIndices=getRandomIndices(tempSize);//获取随机划分位置
int tempTrainingSize=(int)(tempSize*paraTrainingFraction);//训练集大小
trainingSet=new int[tempTrainingSize];//训练集大小就是67行随机求得的
testingSet=new int[tempSize-tempTrainingSize];//总大小减去训练集大小就是测试集大小
for(int i=0;i④通过将测试集中的数据逐个与测试集中数据进行距离测量,找到每个测试集数据的k个邻居。在本次实验中,选取欧式距离作为距离度量方式。
public double distance(int paraI,int paraJ) {
double resultDistance=0;
double tempDifference;
switch (distanceMeasure) {//距离测量
case MANHATTAN://曼哈顿距离
for(int i=0;i⑤k个邻居进行投票,最终得到测试数据的预测结果。
public int[] computeNearest(int paraCurrent) {//计算邻居
int[] resultNearests=new int[numNeighbors];
boolean[] tempSelected=new boolean[trainingSet.length];
double tempDistance;
double tempMinimalDistance;
int tempMinimalIndex=0;//记录最小变量位置
//选出最近的位置
for(int i=0;itempMaximalVoting) {//若大于
tempMaximalVoting=tempVotes[i];//替换
tempMaximalVotingIndex=i;//记录
}
}
return tempMaximalVoting;
} ⑥统计预测成功的数据数量,并与测试集总数据数量相除,得到最终结果:预测准确度。输出每一个测试集数据的k个邻居,并输出计算得到的预测准确度。
public void predict() {//预测函数
predictions=new int[testingSet.length];
for(int i=0;i五、算法特点
1、KNN算法没有学习过程,亦称为“懒惰学习”。易学易用。
2、虽然算法简单,但算法效果十分出色。
3、算法适应性强,能够用于分类、回归等问题。
4、在某些应用场合,为了防止特征值过大或过小对结果造成影响,因此需要对数据进行归一化处理。
5、算法的复杂度较高。
六、一些问题
1、“邻居”个数的选取,即K的取值。如何选择K值才能达到最好的预测效果?
答:K是一个重要的参数,不同的K值会产生不同的效果。在实际应用中,一般先取一个比较小的K值,然后采用交叉验证法来选取最优的K值。
2、选择哪种距离度量方式来寻找K个“邻居”?
答:可以使用不同距离度量方法进行使用,最后选择预测效果最好的一种度量方式。