机器学习之神经网络:日撸Java三百行day71-80
1、什么是神经网络
神经网络(Neural Network,NN)或人工神经网络(Artificial Neural Network,ANN),是指用大量的简单计算单元(即神经元)构成的非线性系统,它在一定程度上模仿了人脑神经系统的信息处理、存储和检索功能。是对人脑神经网络的某种简化、抽象、模拟。
本文介绍的是一种最常用的神经网络算法,即BP(Back Propagation)神经网络。这是由Rumelhart等人于1985年提出的学习算法。该算法利用输出后的误差来估计输出层的直接前导层的误差,再用这个误差估计更前一层的误差,如此一层一层地反传下去,就获得了所有其他各层的误差估计。

刚开始接触到“神经网络”这个名词时就觉得十分的专业,感觉是难以理解的。但通过阅读一些资料发现,其基本理论以及算法机理还是比较“温柔”的。
·神经网络算法理论
神经网络的结构和基本原理是以人脑的组织结构和活动规律为背景的。神经网络由许多并行运算的简单功能单元——神经元组成,每个神经元有一个输出,它能够连接到许多其他神经元,每个神经元输入有多个连接通路,每一个连接通路对应一个连接权系数。
2、神经网络算法思想
根据神经网络算法理论,我们可以得到一个简单的神经元模型。每个神经元与其他神经元相连,当神经元受到一定刺激时,就会向其相连的神经元发送化学物质。这种现象在日常生活中也十分常见。如:如果手指被针扎了,由于大脑受到了来自手指的信号,那么手马上就会收回。在这个情景中,“疼痛”就成为了刺激,那么我们的“行为”也就成为了输出结果。
·M-P神经元模型
M-P神经元模型是按照生物神经元的结构和工作原理构造出来的一个抽象和简化了的模型,它实际上就是对单个神经元的一种建模。MP指的是该模型的作者McCulloch与Pitts。在这个简单模型中,神经元接收到来自 n n n个其他神经元传递来的输入信号,如:手被针扎了。这些输入信号通过带权重的连接进行传递。毕竟,有一些信号相较于“被针扎了”就显得没那么重要。这里就体现了权重的作用。
神经元受到其他神经元输入的信号后,将它们累加起并与神经元阈值进行比较。若达到了阈值,那么就通过“激活函数”产生神经元的输出。输出值 y y y的表达式为:
y = f ( ∑ i = 1 n ω i x i − θ ) y=f(\sum_{i=1}^{n}\omega _{i}x_{i}-\theta ) y=f(i=1∑nωixi−θ)
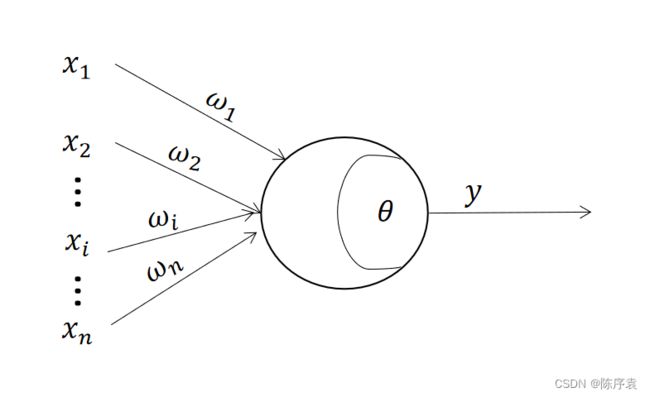
其中, x i x_{i} xi表示来自第 i i i个神经元的输入信号; ω i ω_i ωi代表第 i i i个神经元的连接权重; θ θ θ代表神经元阈值; y y y代表当前神经元输出信号; f f f为激活函数。
在这里的输出信号是通过激活函数(activation function)处理的。激活函数的选择视构建神经网络过程中的重要环节。常用激活函数有线性函数、斜面函数、阶跃函数与 S i g m o i d Sigmoid Sigmoid函数等等。在本实验中使用 S i g m o i d Sigmoid Sigmoid函数。
·阶跃函数
从名字就可以直到,这个函数是“跳跃”的。在数学中,sgn一般是sign的缩写,也称为符号函数。阶跃函数是理想中的激活函数,以一种较为直接的方式来代表神经元的兴奋与抑制状态。当输出值为“1”代表神经元兴奋,即“有痛感”;当输出值为“0”代表神经元抑制,即“没有感觉”。
s g n ( x ) = { 1 , x ≥ 0 ; 0 , x < 0. (1) sgn(x)=\begin{cases} 1, & x\ge 0; \\ 0, & x< 0. \end{cases}\tag{1} sgn(x)={1,0,x≥0;x<0.(1)
同时,由于阶跃函数是理想的,所以它也有一些缺点。诸如:不连续、不光滑。为了弥补这些缺陷,人们常用 S i g m o i d Sigmoid Sigmoid函数。
·Sigmoid函数
sigmoid函数也叫Logistic 函数、 S S S函数,取值范围为(0,1)。它可以将一个实数映射(挤压)到(0,1)的区间,可以用来做二分类。有时也称其为“挤压函数”(squashing function)。
s i g m o i d = 1 1 + e − x (2) sigmoid=\frac{1}{1+e^{-x}}\tag{2} sigmoid=1+e−x1(2)
·BP神经网络
神经网络是由大量的神经元互相连接而构成的网络。根据网络中神经元的互连方式,可以将网络结构分成以下三类:①前馈神经网络;②反馈神经网络;③自组织网络。BP神经网络就属于前馈网络。
BP神经网络主要是靠不断地修正来进行优化与输出。用通俗的语言来解释就是:完成一套试卷,将那些做错的题反馈给学生,让学生们更加重视自己的错题。学生有的放矢的对自己的知识进行夯实优化。进行多次训练后,将错误率降到最低。
该算法的主要思想是:对于 n n n个输入学习样本 { x 1 , x 2 , ⋅ ⋅ ⋅ , x n } \left \{ x^{1} ,x^{2},···,x^{n}\right \} {x1,x2,⋅⋅⋅,xn}以及与其对应的 m m m个输出样本 { t 1 , t 2 , ⋅ ⋅ ⋅ , t m } \left \{ t^{1},t^{2}, ···,t^{m}\right \} {t1,t2,⋅⋅⋅,tm}。用网络的实际输出 { z 1 , z 2 , ⋅ ⋅ ⋅ , z m } \left \{z^{1},z^{2},···,z^{m}\right \} {z1,z2,⋅⋅⋅,zm}与目标矢量 { t 1 , t 2 , ⋅ ⋅ ⋅ , t m } \left \{ t^{1},t^{2}, ···,t^{m}\right \} {t1,t2,⋅⋅⋅,tm}之间的误差来修改其权值。
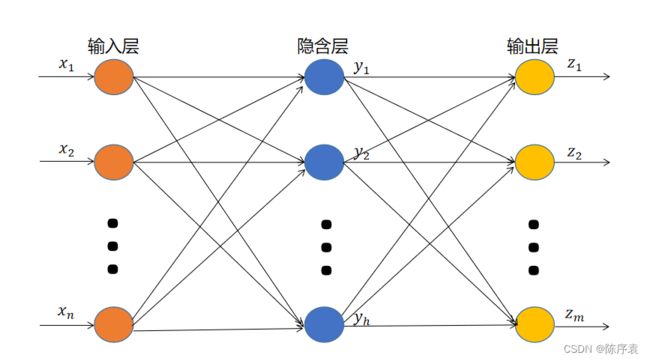
算法的学习过程由正向传播(forward)和反向传播(backPropagation)组成。在正向传播中,输入信息(Input)从输入层经隐含层单元逐层处理后传向输出层。如果在输出层不能得到所期望的输出(Target),就需要“算账”,转入反向传播。将误差信号沿原来的连接通路返回,通过修改各层神经元权值,使得误差信号减小。
·Delta学习规则
在反向传播的过程中,调整边权值是关键一步。Delta学习规则是一种简单的督导学习算法,通过实际输出和期望输出的差别来调整连接边权值。基本思想为:若实际输出比期望输出大,则减小所有输入为正的连接的权重,增大所有输入为负的连接的权重;反之,若实际输出比期望输出小,则增大所有输入为正的连接的权重,减小所有输入为负得连接的权重。其表达式为:
w i j ( t + 1 ) = w i j ( t ) + α ( t i − z i ) x j ( t ) (3) w_{ij}(t+1)=w_{ij}(t)+\alpha (t_{i}-z_{i})x_{j}(t) \tag{3} wij(t+1)=wij(t)+α(ti−zi)xj(t)(3)
其中, w i j w_{ij} wij代表连接权重, α \alpha α代表学习率(learning rate)。 t i t_{i} ti代表期望输出值, z i z_{i} zi代表实际输出值。 x j x_{j} xj代表结点权值。
在本实验中,引入了惯性动量系数mobp。有点类似于粒子群算法中的惯性系数。主要目的是为了维持其本身的连接边权值。引入惯性动量系数后的权重更新表达式为:
w i j ( t + 1 ) = m w i j ( t ) + α ( t i − z i ) x j ( t ) (4) w_{ij}(t+1)=mw_{ij}(t)+\alpha (t_{i}-z_{i})x_{j}(t) \tag{4} wij(t+1)=mwij(t)+α(ti−zi)xj(t)(4)
·正向传播
为了得到输出值,输入信息需要经过若干个隐含层。设输入信息为 x = { x 1 , x 2 , ⋅ ⋅ ⋅ , x n } T x=\left \{ x_{1} ,x_{2},···,x_{n}\right \}^{T} x={x1,x2,⋅⋅⋅,xn}T,隐含层有 h h h个结点。通过隐含层处理后,隐含层输出信息为 y = { y 1 , y 2 , ⋅ ⋅ ⋅ , y h } T y=\left \{ y_{1} ,y_{2},···,y_{h}\right \}^{T} y={y1,y2,⋅⋅⋅,yh}T。输出层有 m m m个结点,它们的输出为 z = { z 1 , z 2 , ⋅ ⋅ ⋅ , z m } T z=\left \{ z_{1} ,z_{2},···,z_{m}\right \}^{T} z={z1,z2,⋅⋅⋅,zm}T。隐含层到输出层之间的激活函数为 f f f,输出层的激活函数为 g g g。激活函数的选择在前面的内容提过了。那么隐含层第 j j j个神经元的输出值 y j y_{j} yj的计算表达式为:
y j = f ( ∑ i = 1 n w i j x i − θ ) = f ( ∑ i = 0 n w i j x i ) (5) y_{j}=f(\sum_{i=1}^{n}w_{ij}x_{i}-\theta )=f(\sum_{i=0}^{n}w_{ij}x_{i})\tag{5} yj=f(i=1∑nwijxi−θ)=f(i=0∑nwijxi)(5)
输出层第 k k k个神经元输出值 z k z_{k} zk的计算表达式为:
z k = g ( ∑ j = 0 h w j k y j ) (6) z_{k}=g(\sum_{j=0}^{h}w_{jk}y_{j})\tag{6} zk=g(j=0∑hwjkyj)(6)
经过正向传播后,就能得到实际输出值 z = { z 1 , z 2 , ⋅ ⋅ ⋅ , z m } z=\left \{z^{1},z^{2},···,z^{m}\right \} z={z1,z2,⋅⋅⋅,zm}。那么实际输出与目标输出之间的误差计算表达式为:
ε = 1 2 ∑ k = 1 m ( t k − z k ) 2 (7) \varepsilon =\frac{1}{2} \sum_{k=1}^{m}(t_{k}-z_{k})^{2}\tag{7} ε=21k=1∑m(tk−zk)2(7)
正向传播不仅得到了输出值,也得到了本次传播的误差。那么反向传播的作用就是通过调整权值,来降低误差。
·反向传播
首先调整隐含层到输出层的权值。 v k v_{k} vk为输出层第 k k k个神经元的输入。 v k v_{k} vk的计算公式为:
v k = ∑ j = 0 h w j k y j (8) v_{k}=\sum_{j=0}^{h}w_{jk}y_{j} \tag{8} vk=j=0∑hwjkyj(8)
得到输入值 v k v_{k} vk后,通过(3)式,就能够调整权值。权值调整迭代公式为:
w j k ( t + 1 ) = w j k ( t ) + α ( t k − z k ) g ′ ( v k ) y j (9) w_{jk}(t+1)=w_{jk}(t)+\alpha(t_{k}-z_{k})g'(v_{k})y_{j}\tag{9} wjk(t+1)=wjk(t)+α(tk−zk)g′(vk)yj(9)
然后,就可以调整输入层到隐含层的权值了。 u j u_{j} uj为隐含层第 j j j个神经元的输入。 u j u_{j} uj的计算公式为:
u j = ∑ i = 0 n w i j x i (10) u_{j}=\sum_{i=0}^{n}w_{ij}x_{i} \tag{10} uj=i=0∑nwijxi(10)
得到输入值 u j u_{j} uj后,依然是通过(3)式对权值进行调整。权值调整迭代公式为:
w i j ( t + 1 ) = w i j ( t ) + α ( t k − z k ) f ′ ( u j ) x i (11) w_{ij}(t+1)=w_{ij}(t)+\alpha(t_{k}-z_{k})f'(u_{j})x_{i}\tag{11} wij(t+1)=wij(t)+α(tk−zk)f′(uj)xi(11)
综合以上内容,我们就能够得到BP神经网络的算法流程:

三、算法的基本流程及操作
本次数据集依然是熟悉的iris,这里就不过多赘述了。代码都有注释,结合上面的内容便于理解算法操作。
①初始化全局变量,并读取数据,设置必要的参数。
Instances datasets;//数据集
int numLayers;//网络层数
int[] layerNumNodes;//每一层的节点数组,[3,4,6,2]代表3个输入节点,中间有2层,每一层分别有4个与6个节点
public double mobp;//惯性系数
public double learningRate;//学习率
Random random=new Random();//随机数
public GeneralAnn(String paraFilename,int[] paraLayerNumNodes,double paraLearningRate, double paramobp) {
//1、读取数据
try {
FileReader tempReader=new FileReader(paraFilename);//读入文件
datasets=new Instances(tempReader);//生成数据集
datasets.setClassIndex(datasets.numAttributes()-1);//设置要决策的属性,即最后一个属性
tempReader.close();//关闭文件
} catch (Exception e) {
System.out.println("Error occurred while trying to read" + paraFilename);
System.exit(0);//关闭
// TODO: handle exception
}
//2、设置参数,具体参数有:层数、层中结点数
layerNumNodes=paraLayerNumNodes;//层中结点数
numLayers=layerNumNodes.length;//层数
//调整
layerNumNodes[0]=datasets.numAttributes()-1;//代表4个输入节点,即:四种属性
layerNumNodes[numLayers-1]=datasets.numClasses();//代表属性类别数量,如:二分
learningRate=paraLearningRate;//设置学习率
mobp=paramobp;//设置动量系数
}
②正向传播与反向传播。先在GeneralAnn中写抽象类,然后再在子类SimpleAnn中写具体方法。
public abstract double[] forward(double[] paraInput);//forward优化函数
public abstract void backPropagation(double[] paraTarget);//back惩罚函数
public double[] forward(double[] paraInput) {
//初始化输入层
for(int i=0;i<layerNodeValues[0].length;i++) {
layerNodeValues[0][i]=paraInput[i];//将输入数据复制到第1层中
}
//计算每一层中结点权值
double z;
for(int l=1;l<numLayers;l++) {//每一层都要处理
for(int j=0;j<layerNodeValues[l].length;j++) {//隐含层
z=edgeWeights[l-1][layerNodeValues[l-1].length][j];//补偿值
for(int i=0;i<layerNodeValues[l-1].length;i++) {//输入层
z+=edgeWeights[l-1][i][j]*layerNodeValues[l-1][i];//根据边权值调整权值
}//of for i
layerNodeValues[l][j]=1/(1+Math.exp(-z));//使得其不再是线性的
}
}
return layerNodeValues[numLayers-1];//返回层中结点
}
@Override
public void backPropagation(double[] paraTarget) {
//1、初始化输出层
int l=numLayers-1;//从最后一层开始处理
for(int j=0;j<layerNodeErrors[l].length;j++) {
layerNodeErrors[l][j]=layerNodeValues[l][j]*(1-layerNodeValues[l][j])*(paraTarget[j]-layerNodeValues[l][j]);
//将预测误差记录到该数组
}//of for j
//2、向后惩罚,直到处理到第一层
while(l>0) {
l--;//层数更新
for(int j=0;j<layerNumNodes[l];j++) {//当前层
double z=0.0;//工作变量,用于记录通过权值调整后的惩罚值
for(int i=0;i<layerNumNodes[l+1];i++) {//找上一层
if(l>0) {
z+=layerNodeErrors[l+1][i]*edgeWeights[l][j][i];//记录
}//of if
//权值调整
edgeWeightsDelta[l][j][i]=mobp*edgeWeightsDelta[l][j][i]+learningRate*layerNodeErrors[l+1][i]*layerNodeValues[l][j];//每条边的改变量
edgeWeights[l][j][i]+=edgeWeightsDelta[l][j][i];//将改变量加上
if(j==layerNumNodes[l]-1) {
edgeWeightsDelta[l][j+1][i]=mobp*edgeWeightsDelta[l][j+1][i]+learningRate*layerNodeErrors[l+1][i];
edgeWeights[l][j+1][i]+=edgeWeightsDelta[l][j+1][i];
}//of if
}//of for i
layerNodeErrors[l][j]=layerNodeValues[l][j]*(1-layerNodeValues[l][j])*z;
}//of for j
}//of while
}
③训练函数与投票决策函数。前者用于训练神经网络,后者用于选出本次决策的最终类型。
public void train() {
double[] tempInput=new double[datasets.numAttributes()-1];//数组大小为输入属性数量为除决策属性以外的属性数量,即:4
double[] tempTarget=new double[datasets.numClasses()];//数组大小为:决策属性类别数量,即:2
for(int i=0;i<datasets.numInstances();i++) {
for(int j=0;j<tempInput.length;j++) {
tempInput[j]=datasets.instance(i).value(j);//将输入数组填充
}//of for j
Arrays.fill(tempTarget, 0);//用0填充类别标签数组
tempTarget[(int)datasets.instance(i).classValue()]=1;
//训练
forward(tempInput);//前向预测
backPropagation(tempTarget);//反向调整
}
}//of train
public static int argmax(double[] paraArray) {
int resultIndex=-1;//存储最大位置
double tempMax=-1e10;//存储最大值
for(int i=0;i<paraArray.length;i++) {
if(tempMax<paraArray[i]) {//若找到更大的
tempMax=paraArray[i];//替换
resultIndex=i;//替换
}
}
return resultIndex;
}
public double test() {
double[] tempInput=new double[datasets.numAttributes()-1];//输入数组的大小为4,4个属性
double tempNumCorrect=0;//预测正确的个数
double[] tempPrediction;//预测矩阵
int tempPredictedClass=-1;//预测标签
for(int i=0;i<datasets.numInstances();i++) {
for(int j=0;j<tempInput.length;j++) {
tempInput[j]=datasets.instance(i).value(j);//填充数据
}
//训练当前实例
tempPrediction=forward(tempInput);
tempPredictedClass=argmax(tempPrediction);//将票数最多的类别作为最终的预测类别
if(tempPredictedClass==(int)datasets.instance(i).classIndex()) {//若预测与实际值一致
tempNumCorrect++;//预测正确的个数+1
}
}//of for i
System.out.println("Correct: " + tempNumCorrect + " out of " + datasets.numInstances());
return tempNumCorrect/datasets.numInstances();//返回预测正确率
}
④新建SimpleAnn类,继承父类GeneralAnn。其中forward与back函数以及在②中写过了。在子类中初始化全局变量。
public double[][] layerNodeValues;//层中每一个结点的权值,用于forward训练过程;第一个代表每层的维度,第二个代表层中的每个节点
//第一个[]为总层数,第二个[]为层中节点数
public double[][] layerNodeErrors;//层中每一个结点的错误,用于back惩罚过程;第一个代表每层的维度,第二个代表层中的每个节点
//第一个[]为总层数,第二个[]为层中节点数
public double[][][] edgeWeights;//每层之间的边所带权值
//若总层数为3(节点数分别为4 10 3),那么中间就有两条边,第一个[]为2;因此edgeWeights[0]:4*10;edgeWeights[1]=10*3
public double[][][] edgeWeightsDelta;//改变量数组,用于调整边权值,与edgeWeights大小一致
public SimpleAnn(String paraFilename, int[] paraLayerNumNodes, double paraLearningRate, double paramobp) {
super(paraFilename, paraLayerNumNodes, paraLearningRate, paramobp);
//1、层初始化
layerNodeValues=new double[numLayers][];
layerNodeErrors=new double[numLayers][];
edgeWeights=new double[numLayers-1][][];
edgeWeightsDelta=new double[numLayers-1][][];
//2、层内初始化
for(int l=0;l<numLayers;l++) {//每一层都处理
layerNodeValues[l]=new double[layerNumNodes[l]];//定义第二维大小,即该层的节点数
layerNodeErrors[l]=new double[layerNumNodes[l]];//定义第二维大小,即该层的节点数
if(l+1==numLayers) {//若该层为最后一层
break;//结束
}//of if
edgeWeights[l]=new double[layerNumNodes[l]+1][layerNumNodes[l+1]];//边权值为该层与它后面那层之间的边所带权值
edgeWeightsDelta[l]=new double[layerNumNodes[l]+1][layerNumNodes[l+1]];//调整边权值为该层与它后面那层之间的边所带权值
//填充权值数组
for(int j=0;j<layerNumNodes[l]+1;j++) {
for(int i=0;i<layerNumNodes[l+1];i++) {
edgeWeights[l][j][i]=random.nextDouble();//随机初始化权值数组
}//of for i
}//of for j
}//of for l
}
⑤浅测一下:训练次数为5000,学习速率为0.01,惯性动量为0.6。
public static void main(String[] args) {
int[] tempLayerNodes= {4,8,8,3};
SimpleAnn tempNetWork=new SimpleAnn("", tempLayerNodes, 0.01, 0.6);
for(int round=0;round<5000;round++) {//训练5000次
tempNetWork.train();
}//of for
double tempAccuracy=tempNetWork.test();
System.out.println("The accuracy is: " +tempAccuracy);
}