Codeforces Round 862 (Div. 2) 题解
目录
A. We Need the Zero(构造)
题面翻译:
思路:
代码:
B. The String Has a Target(构造)
题面翻译:
思路:
代码:
C. Place for a Selfie
题面翻译:
思路:
代码:
A. We Need the Zero(构造)
There is an array a consisting of non-negative integers. You can choose an integer x and denote bi=ai⊕xfor all 1≤i≤n where ⊕⊕ denotes the bitwise XOR operation. Is it possible to choose such a number x that the value of the expression b1⊕b2⊕…⊕bnequals 0?
It can be shown that if a valid number xexists, then there also exists x such that (0≤x<28
Input
Each test contains multiple test cases. The first line contains the number of test cases t (1≤t≤1000. The description of the test cases follows.
The first line of the test case contains one integer n (1≤n≤103) — the length of the array a.
The second line of the test case contains n integers — array a (0≤ai<28).
It is guaranteed that the sum of n over all test cases does not exceed 103.
Output
For each set test case, print the integer x (0≤x<28) if it exists, or −1 otherwise.
Example
input
5
3
1 2 5
3
1 2 3
4
0 1 2 3
4
1 2 2 3
1
1
output
6 0 3 -1 1
Note
In the first test case, after applying the operation with the number 66 the array bbecomes [7,4,3], 7⊕4⊕3=0.
There are other answers in the third test case, such as the number 0.
题面翻译:
给你一个数列a,找一个数x,让a异或x构成数列b,然后数列b的异或 为0
思路:
签到,发现n偶数把a异或起来,若为0,则x=0,否则无法构造
n奇数,x就是a的异或
代码:
#include
using namespace std;
typedef long long ll;
int main(){
int T;
cin>>T;
while(T--){
int n;
cin>>n;
int ans=0;
for(int i=1;i<=n;i++){
int t;
cin>>t;
ans^=t;
}
if(n%2==0){
if(ans==0)cout<<0< B. The String Has a Target(构造)
You are given a string s. You can apply this operation to the string exactly once: choose index i and move character si to the beginning of the string (removing it at the old position). For example, if you apply the operation with index i=4 to the string "abaacd" with numbering from 1, you get the string "aabacd". What is the lexicographically minimal†† string you can obtain by this operation?
††A string a is lexicographically smaller than a string b of the same length if and only if the following holds:
- in the first position where a and b differ, the string a has a letter that appears earlier in the alphabet than the corresponding letter in b.
Input
Each test contains multiple test cases. The first line contains the number of test cases t (1≤t≤104). The description of the test cases follows.
The first line of each test case contains a single integer n (1≤n≤105) — the length of the string.
The second line of each test case contains the string s of length n, consisting of lowercase English letters.
It is guaranteed that the sum of n over all test cases does not exceed 105105.
Output
For each test case, on a separate line print the lexicographically smallest string that can be obtained after applying the operation to the original string exactly once.
Example
input
4
3
cba
4
acac
5
abbcb
4
aaba
output
acb aacc abbcb aaab
Note
In the first test case, you need to move the last character to the beginning.
In the second case, you need to move the second letter "a".
In the third set you need to apply the operation with i=1, then the string will not change.
题面翻译:
给你一个字符串,可以把其中一个字符放在最前面,构成一个新字符串,找见字典序最小的新字符串
思路:
遍历小于s[0]的字符,从后往前枚举s中字符,如果找见了,直接放在最前面,就是最小
代码:
#include
using namespace std;
typedef long long ll;
int main(){
int T;
cin>>T;
while(T--){
int n;
cin>>n;
string s;
cin>>s;
char c=s[0];
int flag=0;
for(char i='a';i<=c;i++){
for(int j=s.length()-1;j>=0;j--){
if(s[j]==i){
cout< C. Place for a Selfie
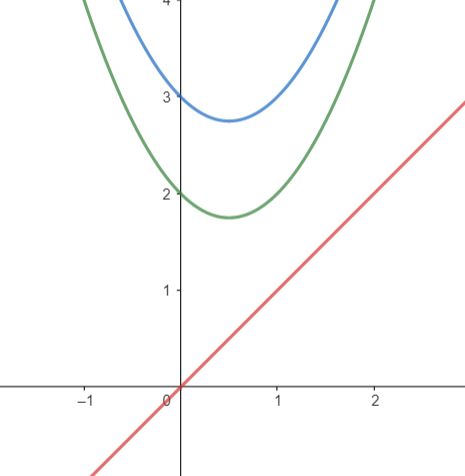
The universe is a coordinate plane. There are n space highways, each of which is a straight line y=kx passing through the origin (0,0). Also, there are m asteroid belts on the plane, which we represent as open upwards parabolas, i. e. graphs of functions y=ax2+bx+c, where a>0
You want to photograph each parabola. To do this, for each parabola you need to choose a line that does not intersect this parabola and does not touch it. You can select the same line for different parabolas. Please find such a line for each parabola, or determine that there is no such line.
Input
Each test contains multiple test cases. The first line contains the number of test cases t (1≤t≤104). The description of the test cases follows.
The first line of each test case contains 2 integers n and m (1≤n,m≤105) —the number of lines and parabolas, respectively.
Each of the next nlines contains one integer k (|k|≤108), denoting a line that is described with the equation y=kx. The lines are not necessarily distinct, k can be equal to 0.
Each of the next mlines contains 33 integers a, b, and c (a,|b|,|c|≤108, a>0) — coefficients of equations of the parabolas ax2+bx+c The parabolas are not necessarily distinct.
It is guaranteed that the sum n over all test cases does not exceed 105105, and the sum m over all test cases also does not exceed 105
Output
For each test case, output the answers for each parabola in the given order. If there is a line that does not intersect the given parabola and doesn't touch it, print on a separate line the word "YES", and then on a separate line the number k — the coefficient of this line. If there are several answers, print any of them. If the line does not exist, print one word "NO".
You can output the answer in any case (upper or lower). For example, the strings "yEs", "yes", "Yes", and "YES" will be recognized as positive responses.
The empty lines in the output in the example are given only for illustration, you do not need to output them (but you can).
Example
input
5
1 2
1
1 -1 2
1 -1 3
2 2
1
4
1 2 1
2 5 1
1 1
0
1 0 0
1 1
100000000
100000000 100000000 100000000
2 3
0
2
2 2 1
1 -2 1
1 -2 -1
output
YES 1 YES 1 YES 1 YES 4 NO YES 100000000 YES 0 NO NO
Note
In the first test case, both parabolas do not intersect the only given line y=1⋅x, so the answer is two numbers 11.
In the second test case, the line y=xand the parabola 2x21 intersect, and also the line y=4x and the parabola x2+2x+1 touch, so these pairs do not satisfy the condition. So for the first parabola, the answer is 11 (y=1, and for the second parabola — 4.
In the third test set, the line and the parabola intersect, so the answer is "NO".
题面翻译:
给你n条直线y=kx,和n条开口向上抛物线y=ax^2+bx+c,判断每条抛物线能不能和某条直线相离,找见这条直线
思路:
判掉所有c小于0的抛物线,剩余的找出第一条大于左边相切那个k的直线, 判断是否相切即可
代码:
#include
using namespace std;
typedef long long ll;
long double k[1000005];
int main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int T;
cin>>T;
while(T--){
ll n,m;
cin>>n>>m;
for(int i=0;i>k[i];
}
sort(k,k+n);
while(m--){
long double a,b,c;
cin>>a>>b>>c;
if(c<=0){
cout<<"NO"<