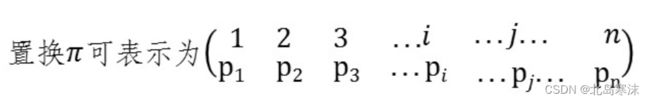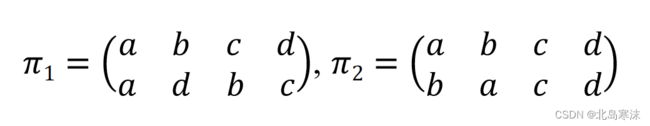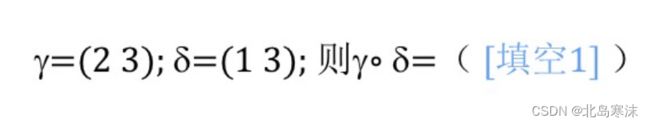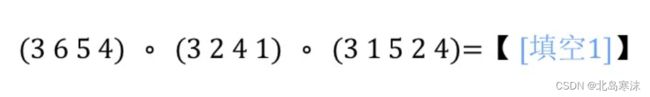近世代数 笔记与题型连载 第八章（置换群）

基本概念

1.置换

置换的定义：有限集合上的一一变换被称为置换。

置换的表示方法：

置换的注意事项：

• 次序无关性：
  
• 与排列的对应性：每一个置换都对应于唯一一个该组元素的重排列方式。反过来，一个重排列也唯一对应一个该组元素的置换方式。

2.置换的复合

对称群的定义：对于一个含有n个元素的集合S，将S上的所有不同置换所组成的集合Sn称为对称群。

左复合和右复合的概念：

对称群的性质：由一个对称群和左复合运算构成的代数系统是一个群。被称为集合S的对称群。

3.置换群

置换群的定义：由对称群和左复合运算构成的群，其中的任何一个子群都被称为集合S上的一个置换群。对称群（代数系统）本身也是一个置换群。

4.置换的轮换表示

轮换的定义和对换的定义：

轮换的表示方法：

轮换的注意事项：

• 轮换不需要使用逗号进行分隔；
• 没有写在轮换中的元素表示用自身来置换自身。
• 幺置换写作（1）。

轮换的性质：对于轮换(a,b,c…z)，同样可以表示为(z,a,b,c…)的形式。也就是说，轮换中可以把结尾元素置于开头位置。

轮换的复合运算：轮换的复合运算实际上就是置换的复合运算，只需要将轮换先转换为置换，然后再进行复合运算即可。

5.轮换的逆

轮换的逆的定理：

6.轮换的不相交

轮换不相交的定义：

不相交轮换的复合可交换性：

不相交轮换的表示定理：

7.轮换的阶

轮换的阶的定义：

相关解释：

• ord用于表示某个置换的阶数。
• 如果该置换用多个轮换的乘积表示，那么该置换的阶数为各个轮换的元素个数的最小公约数。

8.对换

对换的定义：轮换中包含的元素个数被称为轮换的长度，长度为2的轮换被称为对换。

轮换和对换的关系：任意轮换都可以表示为对换的乘积。

9.置换的奇偶性

奇置换和偶置换的定义：可以用奇数个对换的乘积表示的置换称为奇置换，可以用偶数个对换的乘积表示的置换称为偶置换。

交错群的概念：一个集合上的对称群中的所有偶置换构成一个子群，该子群被称为交错群。集合中有多少个元素，就称该子群是几阶交错群。

10.置换的类型

置换类型的定义：

11.正多边形旋转翻转构成的群

二面体群的定义：一般来说，在左复合的作用下，n边正多边形的所有旋转和翻转的集合构成一个n次的2n阶的置换群，这类群统称为二面体群。

相关题型

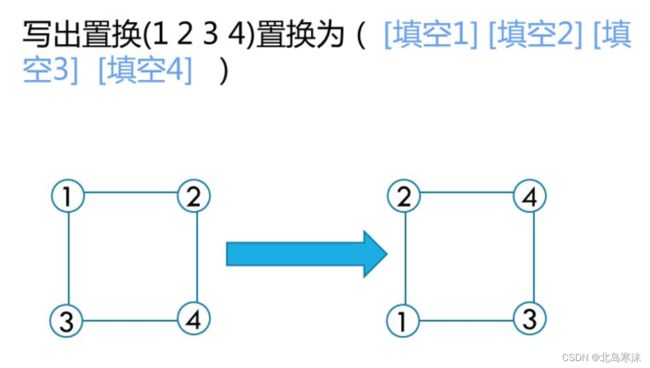
1.置换的概念

解析：本题考查置换的概念。
从图中可以看出，原本在第一个位置的元素被替换成在第二个位置的元素，以此类推。本题的答案是：2413。

2.置换的复合计算

解析：本题考查置换左复合计算。
以初始状态下的元素a为例。由于是左复合计算，因此首先进行Π2置换，将元素a置换为b；接着进行Π1置换，将元素b置换为d，因此总体效果是将元素a置换为d。其他元素以此类推。
综上所述，经过两轮置换后，元素a被置换为d，元素b被置换为a，元素c被置换为b，元素d被置换为c。答案如下：

3.置换的复合计算

解析：本题考查置换的复合计算，原理与上一题完全相同。
经过置换后，元素a被置换为a，元素b被置换为b，元素c被置换d，元素d被置换为c。因此本题的答案为c。

4.置换的复合计算

解析：本题考查置换的复合计算。
通过题意可知，三次置换过程都是使用一个相同的置换，该置换为（J,3,K,A,2,Q）。则经过三次置换后，元素A被置换为3，元素2被置换为Q，元素3被置换为A，元素Q被置换为2，元素J被置换为K，元素K被置换成J。

5.求出一个集合的对称群和置换群

解析：本题考查求一个集合的对称群和置换群。
求一个集合的对称群，只需要按照全排列规则列出该集合上的所有置换，并使得这些置换构成一个集合即可。
在已知一个集合的对称群的基础上寻找该集合的置换群，也就是查找一个指定群的子群，按照上一章的方法求出子群即可。

6.对称群的相关问题

解析：本题考查对称群的相关概念。
求一个已知对称群中所有以自身为逆元的元素，只需要首先需要列出对称群中的所有元素，然后再逐一判断这些元素是否以自身为逆元即可。

7.置换的轮换表示

解析：本题考查置换的轮换表示方法。将按照从上到下，从左到右的顺序求解。
对于第一个置换，各个元素的位置都不发生变化，因此该置换是幺置换，表示为（1）。
对于第二个置换，可以表示为(1 2 3)。
对于第三个置换，可以表示为(1 3 2)。
对于第四个置换，可以表示为(2 3)。
对于第五个置换，可以表示为(1 3)。
对于第六个置换，可以表示为(1 2)。

8.置换的轮换表示

解析：本题考查置换的轮换表示以及轮换的性质。
该置换可以表示为(1 3 2 4) (3 2 4 1) ( 2 4 1 3) (4 1 3 2)。

9.轮换的复合运算

解析：本题考查轮换的复合运算。
只需要将轮换先转换为置换，再进行复合运算即可。对于简单的轮换复合运算，可以直接心算获得结果。
如果起初元素的顺序为123，那么经过第一个轮换后变为321，再经过一次轮换后变为231，那么总的轮换就可以表示为(1 2 3)。

10.轮换的复合运算

解析：本题考查轮换的复合运算。
按照从右到左的轮换顺序，假设初始序列为1 2 3 4 5 6，则经过一次轮换后，序列变为5 4 1 3 2 6，经过两次轮换后，序列变为5 1 3 2 4 6，经过三次轮换后，序列变为4 1 6 2 3 5。
由于可以看出用一个轮换已经无法表示这样一个序列结果，因此需要用两个轮换复合表示。该复合轮换为(4 2 1)(6 5 3)。

11.轮换的逆的计算

解析：本题考查轮换的逆的计算。
根据轮换的逆的定理，后一个轮换的逆即为将轮换中的各个元素逆序，即(2 3 1)。之后需要分别进行(2 3 1) (1 2 3 4)和(1 3 2)三个轮换，可以算出得到的新序列为4 3 1 2，因此复合后的轮换可以表示为(1 4 2 3)。

12.将置换表示为不相交的轮换的形式

解析：本题考查将置换表示为不相交的轮换的形式。
根据所给出的置换可以看出，该置换可以分为(1 2 3 8)和(4 5 7 4)两个独立的部分（不考虑幺置换(6)），因此该置换可以表示为(1 2 3 8)(4 5 7 4)。

13.轮换的阶的有关问题

解析：本题考查在已知轮换的阶和轮换的某次幂的情况下求出该轮换。

14.轮换的阶的有关问题

解析：本题与上一道题目类似。
基本思路是将所要求的置换通过该置换阶数表示为一个置换的幂的形式，再将该幂转化为已知置换的幂的形式进行求解即可。

15.将轮换表示为对换的乘积的形式

解析：本题考查将轮换转换为对换的乘积形式。只需要参考转换公式即可。
由于本身该轮换就是表示为一个子轮换和一个对换的乘积，因此只需要将前面一部分的子轮换修改为用对换的乘积表示即可。
根据公式可知，(1 3 2 5 4 8)可以表示为(1 8)(1 4)(1 5)(1 2)(1 3)，最后合并上(6 9)，得到的最终对换乘积为(1 8)(1 4)(1 5)(1 2)(1 3)(6 9)。

16.判断置换的奇偶性

解析：本题考查置换的奇偶性的概念，只需要按照定义判定即可。
首先应该将该置换表示为一个轮换的形式，接着把该轮换表示为多个对换的乘积形式。如果最终表示为奇数个对换的乘积，那么就是奇置换，否则是偶置换。
本题的答案是奇置换。

17.判断置换的奇偶性

解析：本题考查置换的奇偶性，和上一题的过程类似，只需要按照定义判定即可。
可以简化的是，将置换表示为轮换的乘积后，每一个轮换能够分解出的对换的个数是该轮换的长度减一，因此可以不用写出具体对换乘积便可以判断该置换是奇置换还是偶置换。
本题中对换的个数为5，所以是奇置换。

18.求给定集合的交错群

解析：本题考查集合的交错群。只需要将该集合的对称群的所有置换中的偶置换单独构成一个集合即可。
A4={(1),(12)(34),(13)(24),(14)(23),(123),(132),(124),(142),(134),(143),(234),(243)}

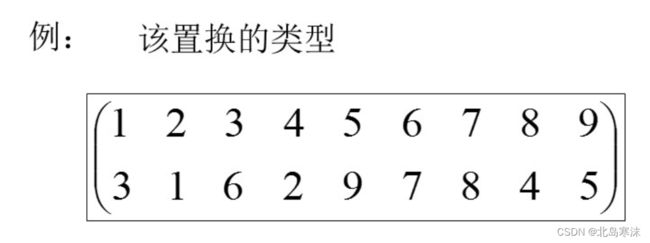
19.置换的类型判断

解析：本题考查置换的类型判断。
由于该置换可以表示为(1 3 6 7 8 4 2)(5 9)，因此置换的类型为7¹2¹型置换。

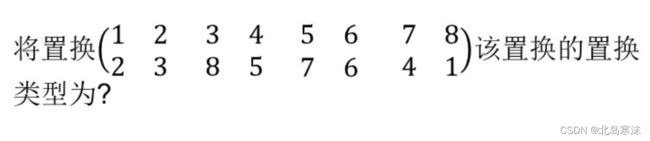
20.置换的类型判断

解析：本题考查置换的类型判断。过程与上一题类似，因此此处不再赘述。