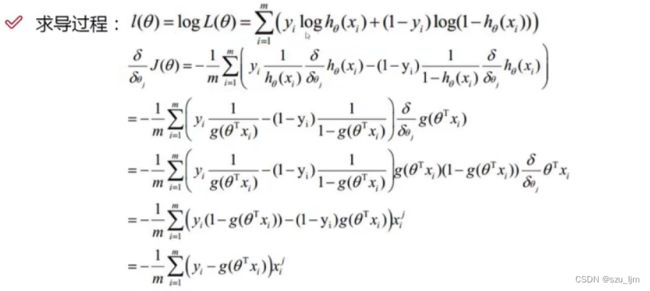Python机器学习入门--逻辑回归学习笔记
文章目录
- 一、逻辑回归简介
- 二、逻辑回归的数学原理
-
- 1. Sigmoid函数
- 2. 预测回归与分类的转化
- 3. 似然函数
- 4. 求偏导和参数更新
- 5. S o f t m a x Softmax Softmax 多分类
- 三、Python实现逻辑回归和 s o f t a m x softamx softamx 多分类
- 总结
一、逻辑回归简介
在机器学习中,我们需要大量样本数据去训练模型来使模型的效果变得越来越好,神经网络和深度学习就是典型的需要大量样本数据才能达到不错效果的模型,一旦遇到样本数据量少的情况就会大打折扣,所以我们有时候需要一些简单的模型,例如逻辑回归就可以在样本量小的情况下有相对较好的表现。
Logistic Regression 虽然被称为逻辑回归,但其实际上是分类模型,并常用于二分类。Logistic 回归的本质是假设数据服从这个分布,然后使用极大似然估计做参数的估计。
二、逻辑回归的数学原理
逻辑回归模型咋一听像是一个解决回归问题的模型,但实际上它是一个利用回归原理进行二分类的分类模型,所以在数学原理上它与线性回归具有很多相同点。
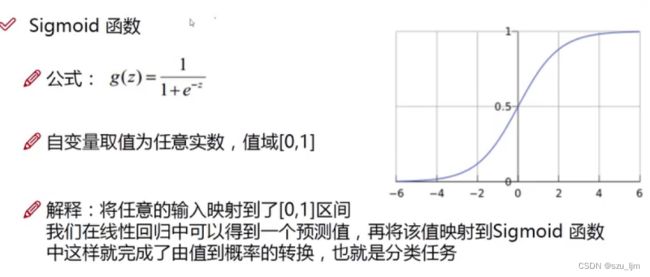
1. Sigmoid函数
S i g m o i d Sigmoid Sigmoid 函数是常用的激活函数之一,它被用来对样本数据进行非线性变换。 S i g m o i d Sigmoid Sigmoid 函数是经典 S型曲线, 在工程、统计学等领域被广泛应用,也是生物学中常见的S型函数,也称为S型生长曲线;在信息科学中,由于其单增以及反函数单增等性质, S i g m o i d Sigmoid Sigmoid 函数常被用作神经网络的激活函数,但是作为神经网络的激活函数它也有其弊端,就是在两侧会出现梯度消失的现象
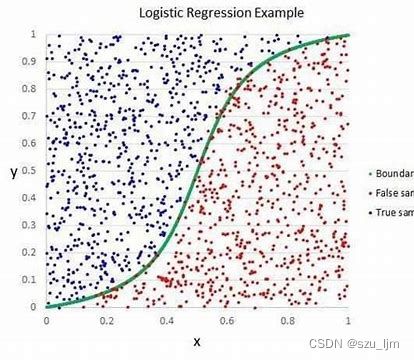
在逻辑回归模型中,我们将样本数据通过 S i g m o i d Sigmoid Sigmoid 函数映射到区间 [ 0 , 1 ] [0,1] [0,1],而概率的取值又刚好在 [ 0 , 1 ] [0,1] [0,1],所以我们就可以将回归预测的结果转化为概率值来实现样本数据的二分类。在数学中, S i g m o i d Sigmoid Sigmoid 函数是关于点 ( 0 , 1 2 ) (0, \frac{1}{2}) (0,21) 中心对称的函数,其趋势也符合客观数据分布,即越靠近均值的数据分布越密集,越远离均值的数据分布越稀疏。
2. 预测回归与分类的转化
逻辑回归和线性回归的数学原理有很多相似点,它们都是对特征及其标签进行矩阵运算,然后都会用到似然函数来构造损失函数,用梯度下降法进行参数更新迭代以寻求最小损失。
不同的是,逻辑回归会先将预测函数放到 S i g m o i d Sigmoid Sigmoid 函数进行非线性变换,将特征和权重参数的乘积转化为概率,所以预测函数中的元素就是概率,标签也会相应变为二分类的逻辑数字0和1
h θ ( x ) = 1 1 + e − θ T x h_{\theta}(x) = \frac{1}{1 + e^{-\theta^{T}x}} hθ(x)=1+e−θTx1
接着将预测函数转化成概率函数,这个概率函数就在描述你的预测值更倾向于正例还是负例,而属于正例和属于负例的概率之和又是1,所以我们就成功将回归问题转化成分类问题,即这个数据点是否属于这一类,不属于就是另一类,最后我们将概率函数整合为一个表达式方便计算
P ( y ∣ x ; θ ) = ( h θ ( x ) ) y ( 1 − h θ ( x ) ) 1 − y P(y | x;\theta) = (h_{\theta}(x))^{y}(1-h_{\theta}(x))^{1-y} P(y∣x;θ)=(hθ(x))y(1−hθ(x))1−y
3. 似然函数
之前我们大致描述了似然函数的作用,逻辑回归里我们用似然函数对概率进行最可能的估计,求解在何种权重参数 θ \theta θ 中我们能最大地接近理想结果,即在给定标签中分类结果的损失最小化
为了方便计算,我们将似然函数经过对数运算后就能把概率乘积转化为概率求和。为了构造分类结果的最小损失函数,我们将本来需要用梯度上升模块求解对数似然函数的最大解,加个负号转化为用梯度下降模块求解最小解,以及求解最小解的驻点值,驻点值是权重参数的矩阵
4. 求偏导和参数更新
接下来就要对对数似然函数对 θ \theta θ 求偏导,这个过程其实是在对矩阵进行求导运算。求完偏导后我们就可以得到梯度的数学表达式
∇ θ j J ( θ ) = − 1 m ∑ i = 1 m ( y i − 1 1 + e − θ T x ) x i j \nabla_{\theta_{j}} J(\theta) = -\frac{1}{m} \sum_{i=1}^m (y_{i} - \frac{1}{1 + e^{-\theta^{T}x}})x_{i}^{j} ∇θjJ(θ)=−m1i=1∑m(yi−1+e−θTx1)xij
最后我们按照梯度下降算法的思想对权重参数 θ \theta θ 进行更新,其中 α \alpha α 是学习率,一般情况下我们是用小批量梯度下降得方法来更新参数值,最后当损失不再发生明显变化时我们就求得我们得驻点值,即权重参数矩阵,就可以画出最后得分类决策边界
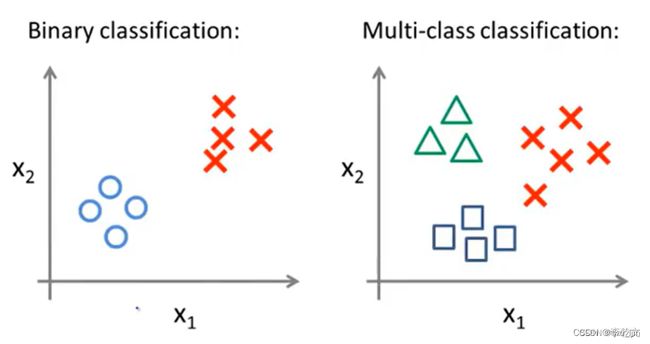
5. S o f t m a x Softmax Softmax 多分类
一般的逻辑回归模型都是解决二分类问题,如果遇到多分类问题,就需要把N种类别取出一种,剩下的类别统一归为一类,当成二分类问题;然后换成另一类,剩下的归为一类,如此遍历,将多类别分类转成很多个二分类问题。 s o f t m a x softmax softmax 多分类是基于逻辑回归来实现的模型,输入一个向量,通过 s o f t m a x softmax softmax 公式映射得到一个概率向量,最后将其分到算出概率最大的一类。
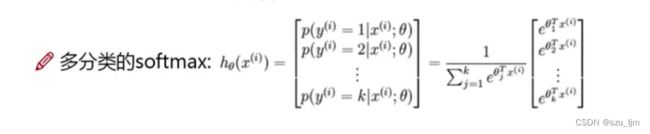
我们输入样本数据后经过 e x e^{x} ex 作用后,再将其占比映射成概率分布,得到每一个特征数据的 s o f t m a x softmax softmax 计算概率,其中每个标签也从原来的逻辑数字0和1转化成多个分类标签
最后用交叉熵来表达 s o f t m a x softmax softmax 多分类的损失函数,交叉熵描述的是在该样本数据映射成的计算概率中,该样本数据属于某一类的概率越接近1,熵越小混乱程度越小,该损失函数的值越小;反之样本数据属于某一类的概率越接近0,熵越大混乱程度越大,该损失函数的值越大。
其实就像你去百货商场买东西,某一区域的商品分类越准确,即混乱程度越低,对于顾客来说买错的损失越小;某一区域的商品分类越凌乱,即混乱程度越高,对于顾客来说买错的损失越大。
三、Python实现逻辑回归和 s o f t a m x softamx softamx 多分类
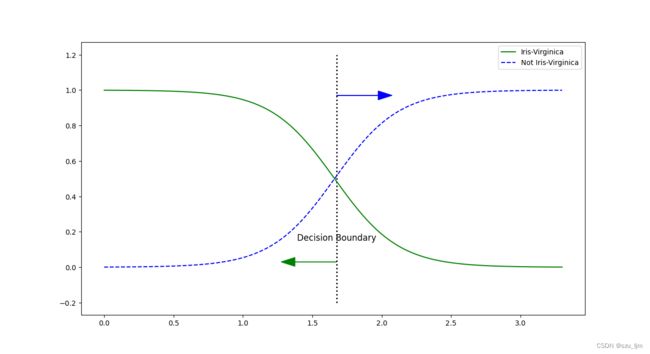
用Python实现逻辑回归要先导入几个常用的包numpy、matplotlib、sklearn,接着我们选取鸳鸯花数据集中花瓣长度特征的数据集,进行花的种类区分,因为是一个二分类问题,所以只有属于这种花和不属于这种花的概率值,接着实例化逻辑回归并训练模型,然后生成测试数据集预测概率,最后做数据可视化展示
import numpy as np
from sklearn import datasets
import matplotlib.pyplot as plt
from sklearn.linear_model import LogisticRegression
iris = datasets.load_iris()
x = iris['data'][:, 3:]
y = (iris['target'] == 2).astype(np.int_)
log_res = LogisticRegression()
log_res.fit(x, y)
x_new = np.linspace(0, 3.3, 200).reshape(-1, 1)
y_porba = log_res.predict_proba(x_new)
print(y_porba)
plt.figure(figsize=(10, 8))
decision_boundary = x_new[y_porba[:, 1] >= 0.5][0]
plt.plot([decision_boundary, decision_boundary], [-0.2, 1.2], 'k:', linewidth=2)
plt.plot(x_new, y_porba[:, 0], 'g-', label='Iris-Virginica')
plt.plot(x_new, y_porba[:, 1], 'b--', label='Not Iris-Virginica')
plt.text(decision_boundary, 0.15, 'Decision Boundary', fontsize=12, color='k', ha='center')
plt.arrow(decision_boundary[0], 0.03, -0.3, 0, head_width=0.05, head_length=0.10, color='g')
plt.arrow(decision_boundary[0], 0.97, 0.3, 0, head_width=0.05, head_length=0.10, color='b')
plt.legend()
plt.show()
用Python实现 s o f t a m x softamx softamx 多分类也要先导入几个常用的包numpy、matplotlib、sklearn,接着我们选取鸳鸯花数据集中花瓣长度和宽度两个特征的数据集,进行花的三个种类区分,因为是一个三分类问题,所以每个数据点会生成三个概率值,接着实例化逻辑回归指定参数为多分类并训练模型,然后生成测试数据集来预测概率和决策边界,最后做数据可视化展示,数据可视化需要用到棋盘格形态,其中主要画出散点分布,决策边界和概率值等高线
import numpy as np
from sklearn import datasets
import matplotlib.pyplot as plt
from sklearn.linear_model import LogisticRegression
from matplotlib.colors import ListedColormap
iris = datasets.load_iris()
x = iris['data'][:, (2, 3)]
y = iris['target']
softmax_reg = LogisticRegression(multi_class='multinomial', solver='lbfgs')
softmax_reg.fit(x, y)
x0, x1 = np.meshgrid(np.linspace(0, 10, 600).reshape(-1, 1), np.linspace(0, 6, 350).reshape(-1, 1), )
x_new = np.c_[x0.ravel(), x1.ravel()]
y_proba = softmax_reg.predict_proba(x_new)
y_predict = softmax_reg.predict(x_new)
zzl = y_proba[:, 1].reshape(x0.shape)
zz = y_predict.reshape(x0.shape)
plt.figure(figsize=(10, 8))
plt.plot(x[y==2, 0], x[y==2, 1], 'g^', label='Iris-Virginica')
plt.plot(x[y==1, 0], x[y==1, 1], 'bs', label='Iris-Versicolor')
plt.plot(x[y==0, 0], x[y==0, 1], 'yo', label='Iris-Setosa')
custom_cmap = ListedColormap(['#fafab0', '#9898ff', '#a0faa0'])
plt.contourf(x0, x1, zz, cmap=custom_cmap)
contour = plt.contour(x0, x1, zzl, cmap=plt.cm.brg)
plt.clabel(contour, inline=1, fontsize=10)
plt.xlabel('Petal Length', fontsize=8)
plt.ylabel('Petal Width', fontsize=8)
plt.legend(loc='center left')
plt.axis([0, 8, 0, 5])
plt.show()
总结
以上是逻辑回归模型的学习笔记,本笔记简单的介绍了逻辑回归的数学原理以及Python实现的思路,逻辑回归算得上是有监督的分类问题中比较简单易用的一类模型, s o f t a m x softamx softamx 比较像单层神经网络,在样本数据比较少的情况下 s o f t a m x softamx softamx 的优势更大,毕竟还是那个道理,模型能尽量精简就精简,效果实在不好再上复杂的模型