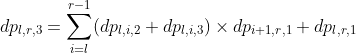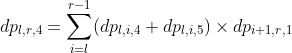CSP-S 2021解题分析

        提高组初赛还是蛮难的，我压着56分的线过来的

1.廊桥分配

        今年T1也是特别的水，导致后三题比较难

        首先有一个关键结论：如果给廊桥编上号，每当一架飞机到达后，如果强制让它进入编号最小的廊桥，这样不会影响进入廊桥飞机的集合，且当廊桥总数增加后，原本在哪个廊桥的飞机，仍旧会进入原来的廊桥。

这个性质也很好理解：新加入廊桥可以视为原先的远机位的一部分，进入新加的这个廊桥的飞机可以视为在原来该进入远机位的飞机中贪心选择一轮。

至此本题已经有了优秀的解决方案：处理出每架飞机在廊桥充足的时候会进入哪个廊桥，然后在差分数组上统计一下即可。

考虑如何实现这个预处理过程：

考虑新建一个时间堆和空闲的编号堆，把所有的飞机按照到达时间排序，如果编号堆中有剩余就取出最小的编号，绑上这家飞机的离开时间扔进时间堆中，每当一架飞机进入之前，先把已经超过离开时间的飞机弹出，释放空闲的廊桥即可。

时间复杂度 。

#include 

using namespace std;

const int Maxn = 1e5 + 5;

struct e {
	int st, ed;
} a[Maxn];
bool cmp(e x, e y) {
	return x.st < y.st;
}

std::priority_queue hp_id;
std::priority_queue > hp_ed; 

int n, m1, m2, ca[Maxn], cb[Maxn];

int main() {
	scanf("%d%d%d", &n, &m1, &m2);
	for(int i = 1; i <= m1; ++i) scanf("%d%d", &a[i].st, &a[i].ed);
	std::sort(a + 1, a + m1 + 1, cmp);
	for(int i = 1; i <= n; ++i) hp_id.push(-i);
	for(int i = 1; i <= m1; ++i) {
		if(!hp_ed.empty()) {
            while(-hp_ed.top().first < a[i].st) {
                hp_id.push(-hp_ed.top().second), hp_ed.pop();
                if(hp_ed.empty()) break;
            }
        }
        if(!hp_id.empty()) {
			int x = -hp_id.top(); hp_id.pop();
			ca[x]++; hp_ed.push(std::make_pair(-a[i].ed, x));
		}
	}
    for(int i = 1; i <= n; ++i) ca[i] += ca[i - 1];
	while(!hp_ed.empty()) hp_ed.pop(); while(!hp_id.empty()) hp_id.pop();
	for(int i = 1; i <= m2; ++i) scanf("%d%d", &a[i].st, &a[i].ed);
	std::sort(a + 1, a + m2 + 1, cmp);
	for(int i = 1; i <= n; ++i) hp_id.push(-i); 
	for(int i = 1; i <= m2; ++i) {
		if(!hp_ed.empty()) {
            while(-hp_ed.top().first < a[i].st) {
                hp_id.push(-hp_ed.top().second), hp_ed.pop();
                if(hp_ed.empty()) break;
            }
        }
		if(!hp_id.empty()) {
			int x = -hp_id.top(); hp_id.pop();
			cb[x]++; hp_ed.push(std::make_pair(-a[i].ed, x));
		}
	}
	for(int i = 1; i <= n; ++i) cb[i] += cb[i - 1]; 
	
	int mx_ans = 0;
	for(int i = 0; i <= n; ++i) mx_ans = std::max(mx_ans, ca[i] + cb[n - i]);
	printf("%d", mx_ans);
	
	return 0;
}

2.括号序列    

        首先肯定是区间dp，令 表示从位置i到位置j一共的合法序列总情况数量。

但是不同的形态可能会有不同的转移，如：(S)这种只能从S转移过来等等。所以只开两维的dp状态必然是不够的。

直接将方法吧。将两位的dp扩充为三维，第三位表示不同的形态种类，dp状态就变成了 。没种状态表示：

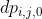• ​: 形态如***...*的括号序列（即全部是*）。

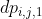• ​: 形态如(...)的括号序列（即左右直接被括号包裹且最左边括号与最右边的括号相互匹配）。

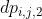• ​: 形态如(...)**(...)***的括号序列（即左边以括号序列开头，右边以*结尾）。

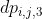• ​: 形态如(...)***(...)*(...)的括号序列（即左边以括号序列开头，右边以括号序列结尾，注意：第2种形态也属于这种形态）。

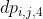• ​: 形态如***(...)**(...)的括号序列（即左边以*开头，右边以括号序列结尾）。

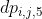• ​: 形态如***(...)**(...)**的括号序列（即左边以*开头，右边以*结尾，注意：第1种形态也属于这种形态）。

设定完状态以后，转移就直接出来了，注意：为了防止连续超过k个*一起出现，转移的时候不能把两段*拼接起来，在状态1的时候暴力判断一下两端的距离是否是的，是的才能转移。

作为一篇题解，转移虽然很简单，但是好得说一下吧。

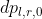• （直接特判）

• • 没什么好解释的

• 

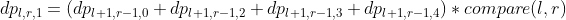
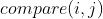• •  表示第i位与第j位能否配对成括号，能则为1，否则为 0。
• • 加括号时，里面可以是全*，可以是有一边是*，也可以是两边都不是*，唯独不能两边都是*且中间有括号序列。

• 

• • 左边以括号序列开头且以括号序列结尾的是第3种，右边接一串*，是第0种。

• 

• • 左边以括号序列开头，结尾随便，符合的有第2和第3种，右边接一个括号序列，是第1种。
• • 记得加上直接一个括号序列的。

• 

• • 左边以*开头，结尾随便，符合的有第4和第5种，右边接一个括号序列，是第1种。

• 

• • 左边以*开头，以括号序列结尾，符合的是第4种，右边接一串*，是第0种。
• • 记得加上全是*的。

最后，答案必须以括号序列开头，以括号序列结尾，所以直接是 ​。

这样，初始状态也就没什么问题了，对于所有的i满足 1≤i≤n，有 。

最终时间复杂度 不到，（后半部分填不满 ）。

记得开long long，并且取模。

#include
using namespace std;
#define ll long long
#define For(i,j,k) for(register int i=j;i<=k;i++)
#define Rof(i,j,k) for(register int i=j;i>=k;i--)
#define ckmx(a,b) if(a

3.回文

        比 T2 简单的 T3 这辈子不多了……

感觉我的做法挺简单的。

分析

由于每一步只能从  的两端之一取一个数字放在 的末尾，所以对第一步的操作分类。

这里只考虑第一步取 'L' 的情况，第一步取 'R' 的情况就不再赘述（除字典序外思路相同）。

找到有且仅有的那个 x 满足。

由于对应​，则必然​ 对应，即中​ 最后一个被取到。

于是题目转化成：

c是一个元素从顶至底为的栈。

d是一个元素从底至顶为的栈。

'L'表示取出 c 的栈顶元素，'R'表示取出 d 的栈顶元素，求使得两个栈的取出序列回文的字典序最小的操作序列。

突然变简单了……

把 c 和 d 都看作双端队列（即栈底可以取出元素）。

重复作这两个步骤直至 c,dc,d 皆为空：

1. 找到一个既存在于 c,dc,d 的（一个或两个）栈顶，又存在于 c,dc,d 的（一个或两个）栈底的元素，若有两个这样的元素，优先选择存在于 cc 栈顶的那个（字典序最小）。若找不到，输出 -1−1 表示无解。

2. 栈顶和栈底各删掉一个这个元素，更新操作序列。

晕了？举个例子（样例 palin1.in 中第一组）：

 4.交通规划

        引子， 2 的解法

对于 k<2，显然可以全部染成附加点的颜色，答案即为0

对于k=2，若此时两个附加点颜色相同，显然答案也为0；

否则整张图一定会被染成一白一黑的两个连通块

（比如这样：）

可以发现原图是一张平面图。特别的，这里认为存在附加点的射线将原本的仅一个 无界面（即那个不在平面图内部，面积无穷大的面）划分为了多个无界面，且对偶图中无界面之间不连边

若我们建出原图的对偶图：对偶图每条边的边权为和它相交的原图的边权。可以发现，答案即为对偶图上两个对应无界面的结点间的最短路

于是对每次询问跑一次 dijkstra 即可。只有无界面对应的结点需要在每次询问时新建。该部分分的复杂度即为

对于所有数据的解法

由部分分做法以及一定程度手玩的启发，可以想到：考虑将相邻的不同颜色附加点射线间的结点两两配对（容易注意到这样的结点个数一定为偶数或 1；结点数为1时显然仅存在一种颜色附加点，答案为0）并分别按 的做法求最短路，再去掉这些最短路对应的原图的边集，那么答案方案所需要去掉的边集一定为某种配对方案对应的边集

（图中红色结点为需要配对的结点，淡蓝色区域则为该结点对应的无界面：）

按照这个结论能得到一个合法的方案是显然的：如此两两配对后，所有配对结点间的路径一定能将不同颜色的附加点划分到不同的连通块中；若有两条路径存在部分重合，那么交换配对结点一定会有更小的边权和，因此最终得到的方案也不会有路径重合（即不会有重复的需要去掉的边）

但要证明其最优性还需证明答案方案一定为结论所述的形式：即不同色附加点射线间结点两两配对求路径得到的路径集合对应的原图边集；或者换句话说，不存在类似从相邻的同色附加点射线间穿出的路径，或在网格内部断掉的路径这种奇奇怪怪的情况。这可能需要费一点功夫，但大体也就是分类讨论并反证。

求路径和最小的配对方案可以 直接 dp，具体此处略。最终复杂度可以做到 

另外还有一个小细节。求出的最短路可能长这样：

所以对于同色附加点射线间的结点也必须要建点，并和网格内的结点连双向边

#include 
using namespace std;
const int MAXN=510;
struct P {
    int x,y,z;
}p[MAXN];
int n,m,t,k,a[MAXN][MAXN],b[MAXN][MAXN],poi[2][MAXN],dist[30][MAXN*MAXN],vis[MAXN*MAXN],rev[MAXN*MAXN];
int col[MAXN],id[MAXN],dp[MAXN][MAXN];
int hs (int a,int b) {return a*(m+1)+b;}
pair  revhs (int x) {return make_pair(x/(m+1),x%(m+1));}
bool cmp (P a,P b) {return a.y > q;
    q.push(make_pair(0,pt));
    while (q.size()) {
        pair  aa=q.top();
        q.pop();
        if (vis[aa.second]) {continue;}
        vis[aa.second]=1;
        pair  bb=revhs(aa.second);
        if (bb.first!=0&&dist[xb][hs(bb.first-1,bb.second)]>dist[xb][aa.second]+b[bb.first][bb.second]) {
            dist[xb][hs(bb.first-1,bb.second)]=dist[xb][aa.second]+b[bb.first][bb.second];
            q.push(make_pair(-dist[xb][hs(bb.first-1,bb.second)],hs(bb.first-1,bb.second)));
        }
        if (bb.first!=n&&dist[xb][hs(bb.first+1,bb.second)]>dist[xb][aa.second]+b[bb.first+1][bb.second]) {
            dist[xb][hs(bb.first+1,bb.second)]=dist[xb][aa.second]+b[bb.first+1][bb.second];
            q.push(make_pair(-dist[xb][hs(bb.first+1,bb.second)],hs(bb.first+1,bb.second)));
        }
        if (bb.second!=0&&dist[xb][hs(bb.first,bb.second-1)]>dist[xb][aa.second]+a[bb.first][bb.second]) {
            dist[xb][hs(bb.first,bb.second-1)]=dist[xb][aa.second]+a[bb.first][bb.second];
            q.push(make_pair(-dist[xb][hs(bb.first,bb.second-1)],hs(bb.first,bb.second-1)));
        }
        if (bb.second!=m&&dist[xb][hs(bb.first,bb.second+1)]>dist[xb][aa.second]+a[bb.first][bb.second+1]) {
            dist[xb][hs(bb.first,bb.second+1)]=dist[xb][aa.second]+a[bb.first][bb.second+1];
            q.push(make_pair(-dist[xb][hs(bb.first,bb.second+1)],hs(bb.first,bb.second+1)));
        }
    }
    return;
}
int main () {
    scanf("%d%d%d",&n,&m,&t);
    for (int i=1;i<=n-1;i++) {
        for (int j=1;j<=m;j++) {scanf("%d",&a[i][j]);}
    }
    for (int i=1;i<=n;i++) {
        for (int j=1;j<=m-1;j++) {scanf("%d",&b[i][j]);}
    }
    for (int i=1;i<=t;i++) {
        for (int i=0;i<=max(n,m);i++) {a[0][i]=a[n][i]=b[i][0]=b[i][m]=0;}
        scanf("%d",&k);
        for (int j=1;j<=k;j++) {scanf("%d%d%d",&p[j].x,&p[j].y,&p[j].z);}
        sort(p+1,p+k+1,cmp);
        int cnt=0,las=0,nw=0;
        for (int j=1;j<=k;j++) {
            if (p[j].y<=m) {a[0][p[j].y]=p[j].x;}
            else if (p[j].y<=m+n) {b[p[j].y-m][m]=p[j].x;}
            else if (p[j].y<=m+n+m) {a[n][m+n+m+1-p[j].y]=p[j].x;}
            else {b[m+n+m+n+1-p[j].y][0]=p[j].x;}
            if (las&&p[j].z!=p[las].z) {
                cnt+=(nw^1);
                poi[nw][cnt]=getnx(p[j].y-1);
                nw^=1;
            }
            if (!las||p[j].z!=p[las].z) {las=j;}
        }
        if (nw==1) {poi[nw][cnt]=hs(0,0);nw^=1;}
        if (cnt==0) {
            printf("0\n");
            continue;
        }
        for (int j=1;j<=cnt;j++) {
            rev[poi[0][j]]=j;
            memset(dist[j],0x3f,sizeof(dist[j]));
            memset(vis,0,sizeof(vis));
            dijkstra(j,poi[0][j]);
        }
        for (int i=1;i<=cnt;i++) {
            col[2*i-1]=col[2*cnt+2*i-1]=0;
            id[2*i-1]=id[2*cnt+2*i-1]=poi[0][i];
            col[2*i]=col[2*cnt+2*i]=1;
            id[2*i]=id[2*cnt+2*i]=poi[1][i];
        }
        for (int i=4*cnt;i>=1;i--) {
            for (int j=i;j<=4*cnt;j++) {
                dp[i][j]=1e9;
                if ((j-i)&1) {
                    if (i&1) {dp[i][j]=dp[i+1][j-1]+dist[rev[id[i]]][id[j]];}
                    else {dp[i][j]=dp[i+1][j-1]+dist[rev[id[j]]][id[i]];}
                    for (int k=i+1;k

 今年怎么NOIP和CSP都不太正常的亚子