基于 SFLA 优化算法训练神经网络(Matlab代码实现)
目录
1 概述
2 运行结果
3 参考文献
4 Matlab代码
1 概述
混合蛙跳算法是2000年由Muzaffar Eusuff和Kevin Lansey提出的一种基于群智能的亚启发式计算优化算法,用于解决离散组合优化问题。作为一种新型的仿生物学智能优化算法,SFLA结合了基于模因(meme)进化的模因演算法(MA,memetic algorithm)和基于群体行为的粒子群算法(PSO,particle swarm optimization)2种群智能优化算法的优点。该算法具有概念简单,调整的参数少,计算速度快,全局搜索寻优能力强,易于实现的特点。混合蛙跳算法主要应用于解决多目标优化问题,例如水资源分配、桥墩维修、车间作业流程安排等工程实际应用问题。
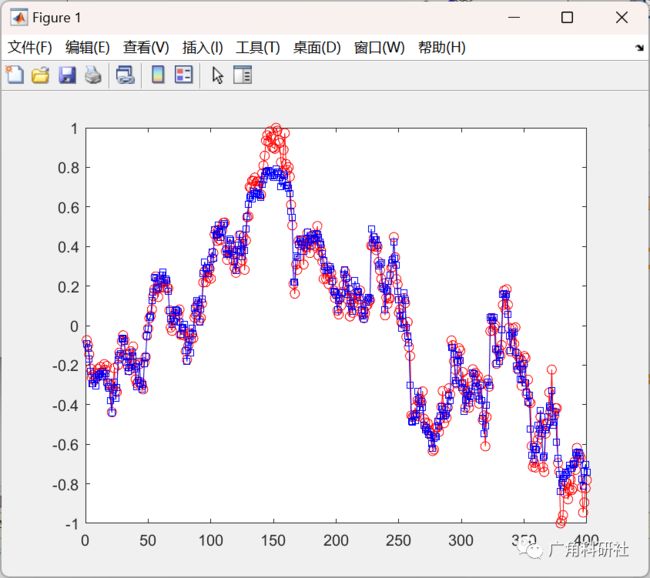
2 运行结果
主函数部分代码:
%% Start of Program
clc
clear
close all
%% Data Loading
[~,testData] = xlsread('test.xls');
[~,trainData] = xlsread('Amozesh.xls');
testData(:,1)=[];
testData(1,:)=[];
trainData(:,1)=[];
trainData(1,:)=[];
Dtrain=[];
for i=1:size(trainData,1)
for j=1:size(trainData,2)
D=str2num(cell2mat(trainData(i,j)));
Dtrain(i,j)=D;
end
end
Dtest=[];
for i=1:size(testData,1)
for j=1:size(testData,2)
D=str2num(cell2mat(testData(i,j)));
Dtest(i,j)=D;
end
end
%%
nTrain=size(Dtrain,1);
nTest=size(Dtest,1);
Data=[Dtrain;Dtest];
X = Data(:,1:end-1);
Y = Data(:,end);
DataNum = size(X,1);
InputNum = size(X,2);
OutputNum = size(Y,2);
%% Normalization
MinX = min(X);
MaxX = max(X);
MinY = min(Y);
MaxY = max(Y);
XN = X;
YN = Y;
for ii = 1:InputNum
XN(:,ii) = Normalize_Fcn(X(:,ii),MinX(ii),MaxX(ii));
end
for ii = 1:OutputNum
YN(:,ii) = Normalize_Fcn(Y(:,ii),MinY(ii),MaxY(ii));
end
%% Test and Train Data
Xtr = XN(1:nTrain,:);
Ytr = YN(1:nTrain,:);
Xts = XN(nTrain+1:end,:);
Yts = YN(nTrain+1:end,:);
%% Network Structure
pr = [-1 1];
PR = repmat(pr,InputNum,1);
Network = newff(PR,[5 OutputNum],{'tansig' 'tansig'});
%% Training
Network = TrainUsing_BSFLA_Fcn(Network,Xtr,Ytr);
%% Assesment
YtrNet = sim(Network,Xtr')';
YtsNet = sim(Network,Xts')';
MSEtr = mse(YtrNet - Ytr)
MSEts = mse(YtsNet - Yts)
RMSEtr =sqrt( mse(YtrNet - Ytr))
RMSEts =sqrt( mse(YtsNet - Yts))
perft = mae(YtrNet - Ytr);
perfs = mae(YtsNet - Yts);
%% Display
figure(1)
plot(Ytr,'-or');
hold on
plot(YtrNet,'-sb');
hold off
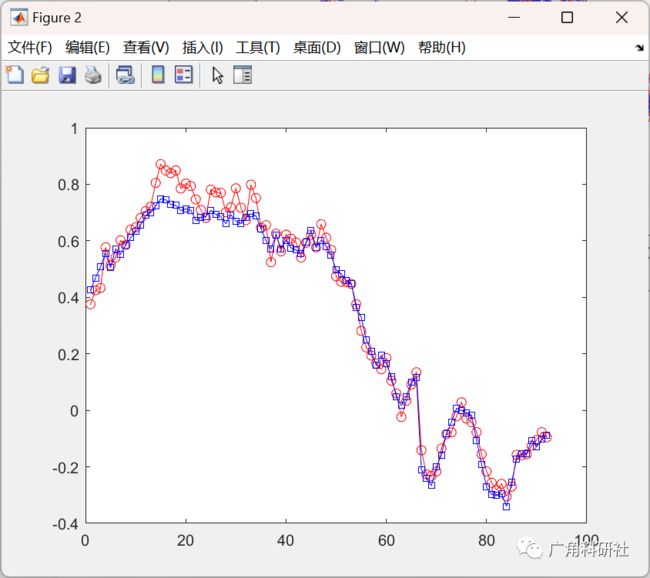
figure(2)
plot(Yts,'-or');
hold on
plot(YtsNet,'-sb');
hold off
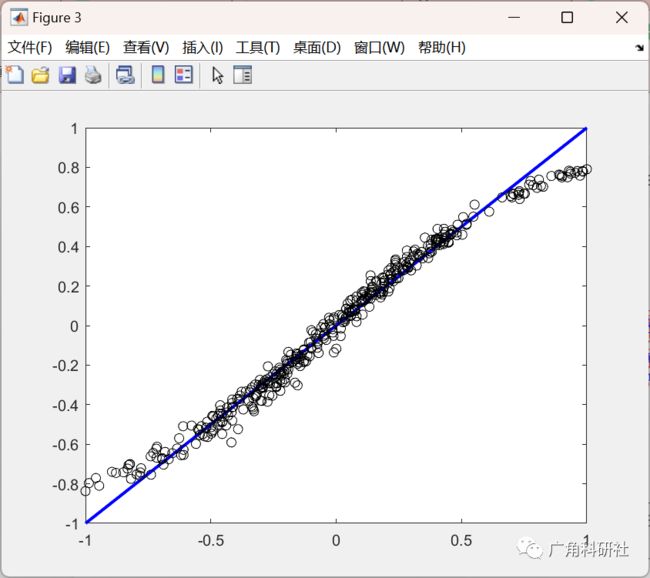
figure(3)
t = -1:.1:1;
plot(t,t,'b','linewidth',2)
hold on
plot(Ytr,YtrNet,'ok')
hold off
figure(4)
t = -1:.1:1;
plot(t,t,'b','linewidth',2)
hold on
plot(Yts,YtsNet,'ok')
hold off
3 参考文献
[1]崔文华,刘晓冰,王伟等.混合蛙跳算法研究综述[J].控制与决策,2012,27(04):481-486+493.DOI:10.13195/j.cd.2012.04.3.cuiwh.014.
部分理论引用网络文献,若有侵权联系博主删除。