免费馅饼的亿点小思路
免费馅饼
题目描述
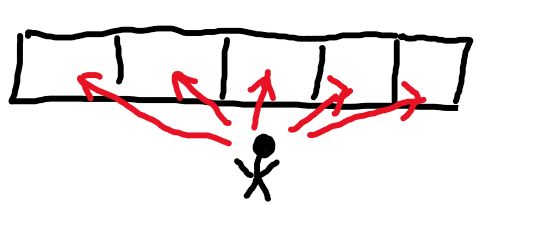
SERKOI最新推出了一种叫做“免费馅饼”的游戏:游戏在一个舞台上进行。舞台的宽度为W格,天幕的高度为H格,游戏者占一格。开始时游戏者站在舞台的正中央,手里拿着一个托盘。下图为天幕的高度为4格时某一个时刻游戏者接馅饼的情景。
游戏开始后,从舞台天幕顶端的格子中不断出现馅饼并垂直下落。游戏者左右移动去接馅饼。游戏者每秒可以向左或向右移动一格或两格,也可以站在原地不动。
馅饼有很多种,游戏者事先根据自己的口味,对各种馅饼依次打了分。同时,在8-308电脑的遥控下,各种馅饼下落的速度也是不一样的,下落速度以格/秒为单位。
当馅饼在某一秒末恰好到达游戏者所在的格子中,游戏者就收集到了这块馅饼。
写一个程序,帮助我们的游戏者收集馅饼,使得所收集馅饼的分数之和最大。
输入格式:
输入文件的第一行是用空格隔开的两个正整数,分别给出了舞台的宽度W(1到99之间的奇数)和高度H(1到100之间的整数)。
接下来依馅饼的初始下落时间顺序给出了所有馅饼的信息。每一行给出了一块馅饼的信息。由四个正整数组成,分别表示了馅饼的初始下落时刻(0到1000秒),水平位置、下落速度(1到100)以及分值。游戏开始时刻为0。从1开始自左向右依次对水平方向的每格编号。
输入文件中同一行相邻两项之间用一个或多个空格隔开。
输出格式:
输出文件的第一行给出了一个正整数,表示你的程序所收集的最大分数之和。
输入样例
3 3
0 1 2 5
0 2 1 3
1 2 1 3
1 3 1 4
输出样例
12
思路:我们正着想会发现些许的问题:
- 比如我们每移动一次,所有的煎饼都会往下面走几格,但这样维护不免太复杂了,我们不妨反着想:
我们可以让小人从下往上走,比如这样
这样我们就不用去维护当前这个馅饼到底走到了哪里,然后因为馅饼下落的速度不一样,所以在一开头就可以做一个操作,把每一个馅饼的高度设置为当前的高度除以当前的下落的速度,并且把这个馅饼的分数也设到这个地方。
这样从下往上走就可以起到等同的作用
设 d p [ i ] [ j ] dp[i][j] dp[i][j]为当前走到了第 i i i行的第 j j j列。
我们再想想 ( i , j ) (i,j) (i,j)可以从哪些地方走过来
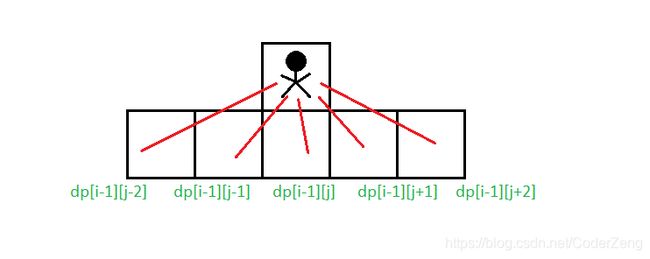
( i , j ) (i,j) (i,j)这个地方,可以从 ( i − 1 , j − 2 ) (i - 1,j - 2) (i−1,j−2), ( i − 1 , j + 1 ) (i - 1,j+1) (i−1,j+1), ( i , j ) (i,j) (i,j), ( i − 1 , j − 1 ) (i - 1,j - 1) (i−1,j−1), ( i − 1 , j − 2 ) (i - 1,j - 2) (i−1,j−2)过来,所以状态转移方程可以这么写:
d p [ i ] [ j ] = m a x ( d p [ i − 1 ] [ j − 2 ] , d p [ i − 1 ] [ j − 1 ] , d p [ i − 1 ] [ j ] , d p [ i − 1 ] [ j + 1 ] , d p [ i − 1 ] [ j + 2 ] ) + a [ i ] [ j ] dp[i][j]=max(dp[i-1][j-2], dp[i-1][j-1], dp[i-1][j], dp[i-1][j+1], dp[i-1][j+2]) + a[i][j] dp[i][j]=max(dp[i−1][j−2],dp[i−1][j−1],dp[i−1][j],dp[i−1][j+1],dp[i−1][j+2])+a[i][j]
a [ i ] [ j ] a[i][j] a[i][j],表示这个位置的分数
- 因为是求最大分数之和,所以取五个值的最大值加上当前这个位置的价值。
#include 完结撒花★,°:.☆( ̄▽ ̄)/$:.°★ 。