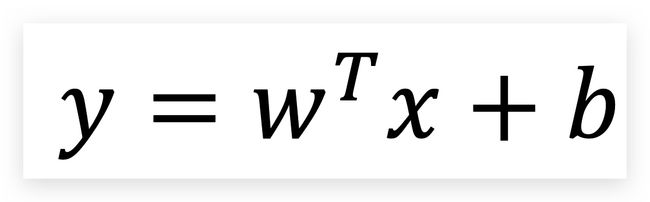线性回归详解及Tensorflow实战
0x01 线性回归概述
线性回归()是利用数理统计中回归分析,来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法
其表达形式为y = w'x+e,e为误差服从均值为0的正态分布
线性回归可能是统计学和机器学习中最著名和最容易理解的算法之一
在统计学中,线性回归是一种对标量响应和一个或多个解释变量(也称为因变量和自变量)之间的关系进行建模的线性方法
一个解释变量的情况称为简单线性回归(simple linear regression)
对于多个,这个过程称为多元线性回归(multiple linear regression)
像所有形式的回归分析一样,线性回归侧重于给定预测因子的值的响应的条件概率分布,而不是所有这些变量的联合概率分布,这是多元分析的领域
线性回归算法发展
机器学习,更具体地说,是预测建模领域,主要关注的是将模型的误差最小化,或以牺牲可解释性为代价,实现最准确的预测
在应用机器学习中,我们将借鉴重用许多不同领域的算法,线性回归在统计领域得到发展,并被作为理解输入和输出数值变量之间关系的模型进行研究,但被机器学习所借鉴,它既是一种统计算法又是一种机器学习算法
Francis Galton
弗朗西斯·高尔顿爵士是一位影响科学、心理、地理和气象领域的英国人。他拥有200的智商,是畅销书作家、手指识别的发明者、统计学家、社会学家、气象学家、地质学家、探险家、差异心理学和遗传学的创始人。他最著名的研究是人类选择性交配,并将其称为优生学。根据他对遗传特征的研究,他还创造了“先天与后天”这个术语
“回归”是由Francis Galton在研究人类遗传问题时提出来的
在他研究父母身高和子女身高时发现“即使父母的身高都‘极端’高,其子女不见得会比父母高,而是有“衰退”(regression)(也称作“回归”)至平均身高的倾向”具体说明一下:高尔顿当时拟合了父母平均身高 x 和 子女平均身高 y 的经验方程:
y:为子女平均身高,这就是我们要预测的真实事物,称为标签
x:为父母平均身高,是用于述数据的输入变量,称为特征
(这种需要通过标签学习的方法称为监督学习)
0x02 线性回归分类
线性回归有许多实际用途,大多数申请可分为以下两大类:
- 如果目标是预测或减少误差,线性回归可用于将预测模型与响应值和解释变量的观测数据集之间的关系
(建立该模型后,如果在没有相应响应值的情况下收集解释变量的附加值,则可以利用拟合的模型对响应进行预测) - 如果目标是解释可归因于解释变量变化的响应变量的变化,则可以应用线性回归分析来量化响应与解释变量之间的关系强度
(特别是确定一些解释变量是否可能与响应完全没有线性关系,或者确定哪些解释变量子集可能包含关于响应的冗余信息)
原因是线性回归已经存在了很长时间(超过200年)。人们从各个可能的角度对它进行了研究
线性回归是一种线性模型,例如假设输入变量(x)与单一输出变量(y)之间存在线性关系的模型
可以使用不同的技术从数据中准备或训练线性回归方程,其中最常见的是普通最小二乘,通常将这种方法准备的模型称为普通最小二乘线性回归或最小二乘回归
0x03 Tensorflow 实战
首先我们知道线性回归的方程:
最常见的事例:房价预测
例如房价的影响因素:位置,大小,环境,楼层...
可以通过不同的因素预测房价
随机值分布
调用matplotlib.pyplot的绘图函数plot()进行绘图
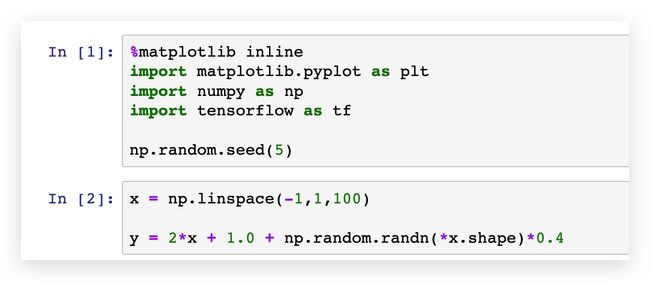
加载matplotlib.pyplot,numpy,tensorflow
并设置随机种子
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import tensorflow as tf
np.random.seed(2)之后生成等差数列,设置噪声,在x值的上下
x = np.linspace(-1,1,100)
y = 2*x + 1.0 + np.random.randn(*x.shape)*0.4利用matplotlib画出生成结果
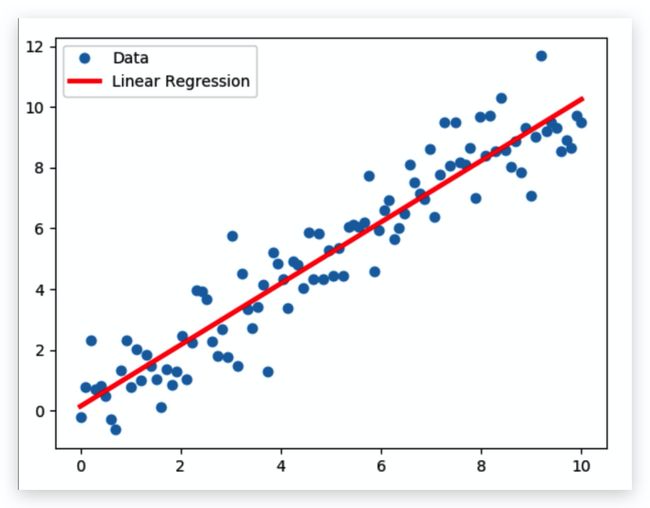
plt.scatter(x, y)
plt.plot(x,2*x+1.0,color='red', linewidth=4)线:实际
点:预测
进行预测
之后构建模型
x2 = tf.placeholder("float",name="x2")
y2 = tf.placeholder("float",name="y2")
def model(x,w,b):
return tf.multiply(x,w)+bw = tf.Variable(1.0, name="w")
b = tf.Variable(0.0, name="b")
pred = model(x2,w,b)定义训练次数以及学习率
采用均方差作为损失函数
train_epochs = 10
learning_rate = 0.05
loss_function = tf.reduce_mean(tf.square(y-pred))
optimizer = tf.train.GradientDescentOptimizer(learning_rate).minimize(loss_function)声明会话
sess = tf.Session()
init = tf.global_variables_initializer()
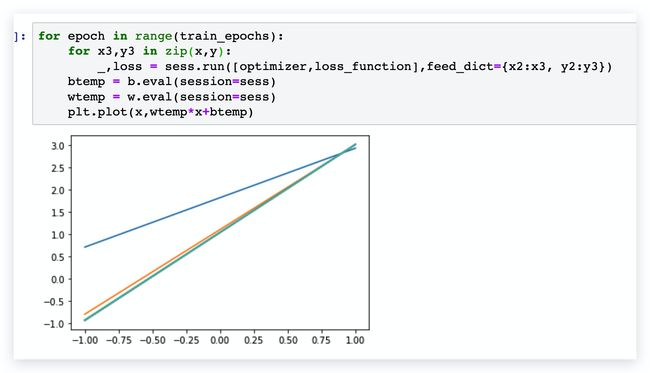
sess.run(init)for epoch in range(train_epochs):
for x3,y3 in zip(x,y):
_,loss = sess.run([optimizer,loss_function],feed_dict={x2:x3, y2:y3})
btemp = b.eval(session=sess)
wtemp = w.eval(session=sess)
plt.plot(x,wtemp*x+btemp)可能会报这种类型的错误,原因是维度不同,修改即可
print(sess.run(w))
print(sess.run(b))plt.scatter(x,y,label='data')
plt.plot(x,x*sess.run(w)+sess.run(b),label='line',color='red',linewidth='4')
plt.legend(loc=2)Reference
https://machinelearningmastery.com/linear-regression-for-machine-learning/
https://www.meiwen.com.cn/subject/uovgsctx.html