计算机组成原理——数据的表示和运算
目录
1.进位计数制
2.BCD码(Binary-Coded Decimal)
2.1 8421码
2.2 余3码
2.3 2421码
3.无符号整数的表示和运算
3.1无符号整数在计算机硬件中如何表示
3.2无符号整数加减法实现原理
4.带符号整数(定点整数)的表示和运算
4.1带符号整数在计算机硬件中如何表示
4.2带符号整数加减法实现原理(补码)
5.定点小数的表示和运算
5.1定点小数在计算机硬件中如何表示
5.2定点小数加减法实现原理
6.算术逻辑单元(ALU)
6.1电路的基本原理
6.2加法器设计
7.并行进位加法器
8.带符号整数(补码)加减法/无符号整数加减法运算器
9.标志位的生成
10.定点数的移位运算
10.1算数移位
10.1.1原码的算数移位
10.1.2反码的算数移位
10.1.3补码的算数移位
10.1.4应用
10.2逻辑移位
10.3循环移位
11.乘法运算
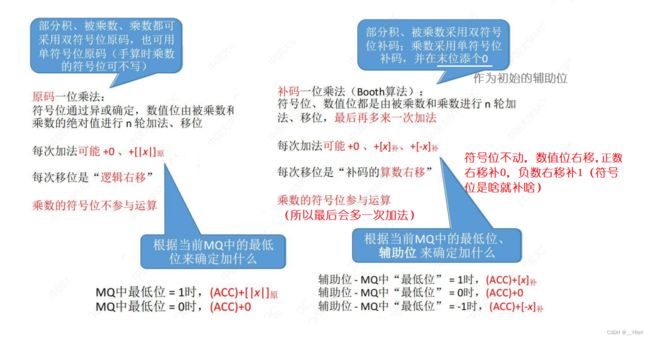
11.1原码一位乘法
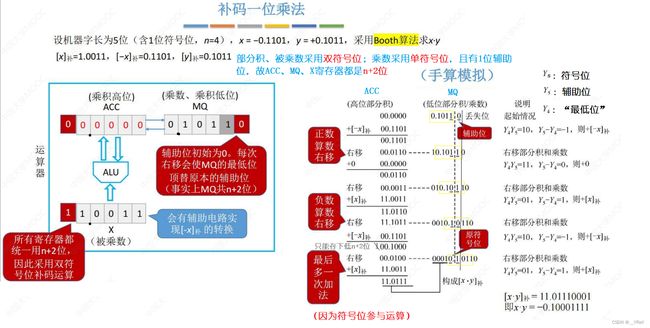
11.2补码一位乘法
12.除法运算
12.1原码除法
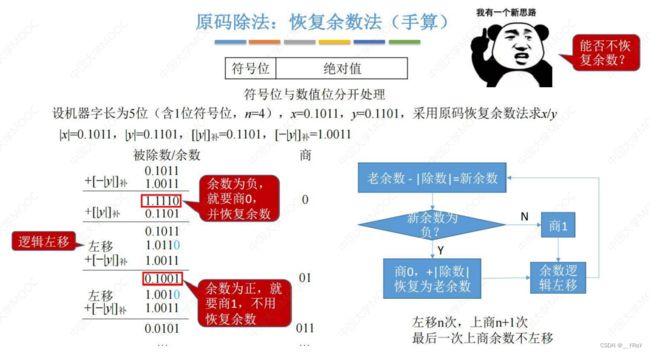
12.1.1恢复余数法
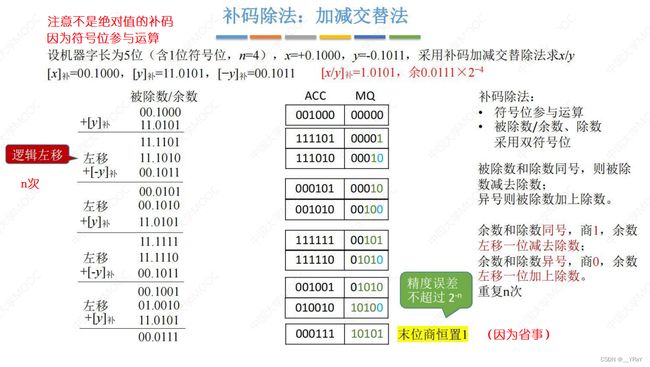
12.1.2加减交替法
12.2补码除法
13.C语言类型转换
14.数据的存储和排列
15.浮点数的表示
16.IEEE754
17.浮点数的运算
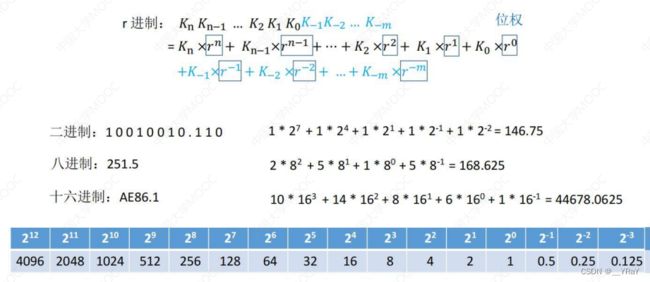
1.进位计数制
r进制计数法:
基数 = r ;每位数码表示 r 种不同状态,逢 r 进1
2/8/16->10:
10->任意进制:
整数:除基取余(先取得的余是整数的低位);小数:乘基取整(先取得的整是小数的高位)
2<->8/16:
注意补位
真值和机器数:
真值:符合人类习惯的数字
机器数:数字实际存到机器里的形式,正负号需要被“数字化”
2.BCD码(Binary-Coded Decimal)
BCD——用二进制编码的十进制
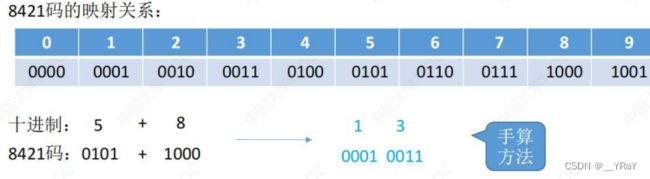
2.1 8421码
有权码
考点:掌握加法运算
合法范围:0000~1001(0~9);非法范围:1010~10010 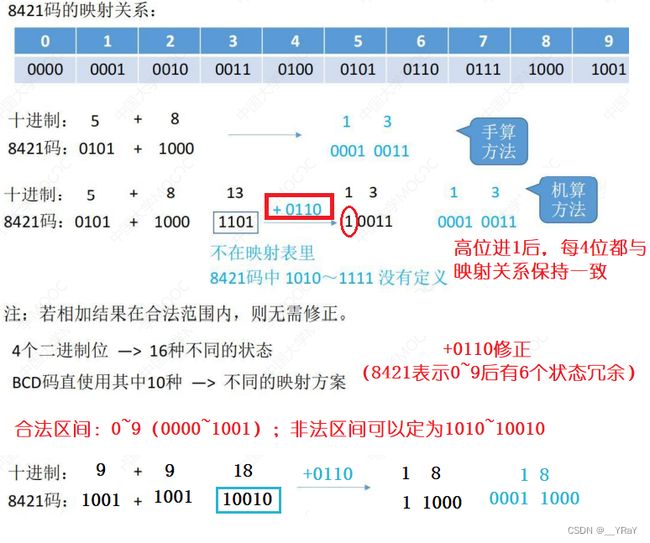
2.2余3码
无权码
2.3 2421码
有权码
表示0~4时最高位位0,表示5~9时最高位为1。(保证编码无歧义)
3.无符号整数的表示和运算
无符号整数即自然数:0,1,2,3……
C语言中的无符号整数:
unsigned short(无符号整数)短整型 2B
unsigned int(无符号整数)整型 4B //二者位数不同表示的数值范围不同
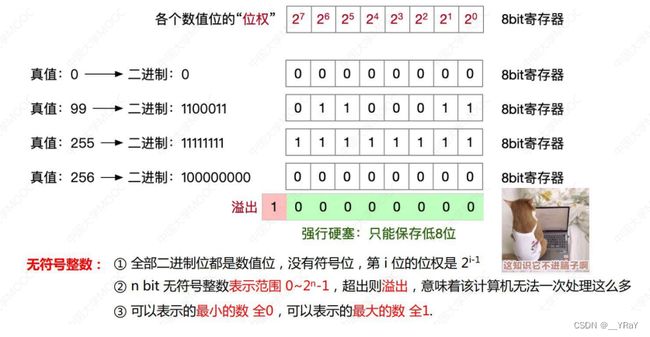
3.1无符号整数在计算机硬件中如何表示
3.2无符号整数加减法实现原理
加法:从最低位开始,按位相加,并往更高位进位(可能会有溢出)
减法:
①"被减数”不变,“减数”全部位按位取反、末位+1,减法变加法
②从最低位开始,按位相加,并往更高位进位
4.带符号整数(定点整数)的表示和运算
带符号整数即整数:……-3,-2,-1,0,1,2,3……
C语言中的带符号整数:
short(带符号整数)短整型 2B
int(带符号整数)整型 4B //二者位数不同表示的数值范围不同
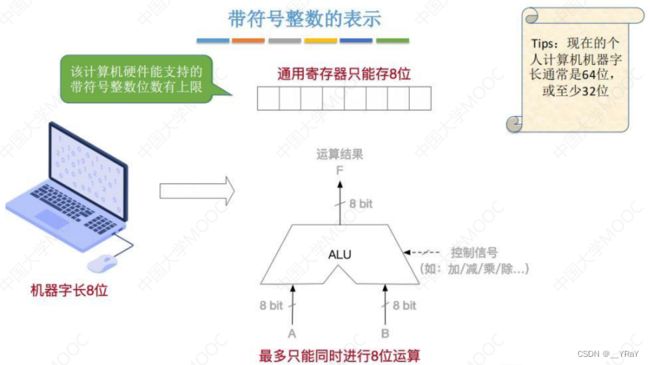
4.1带符号整数在计算机硬件中如何表示
同一个含义用不同编码表示:原码、反码、补码、移码
重点写在前面!!!⭐⭐⭐
原码和反码的合法表示范围完全相同,都有两种方法表示真值0
补码的合法表示范围比原码多一个负数,只有一种方法表示真值0
移码的合法表示范围比原码多一个负数,只有一种方法表示真值0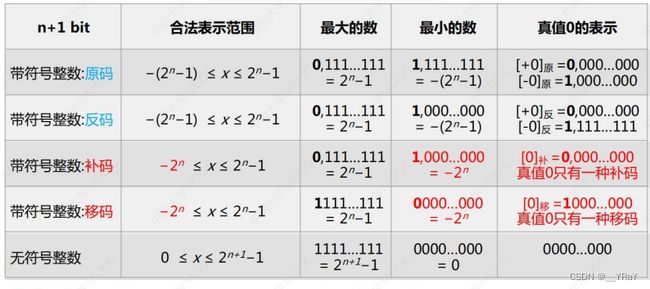
| 7+1 bit | 合法表示范围 | 最大的数 | 最小的数 | 真值0的表示 |
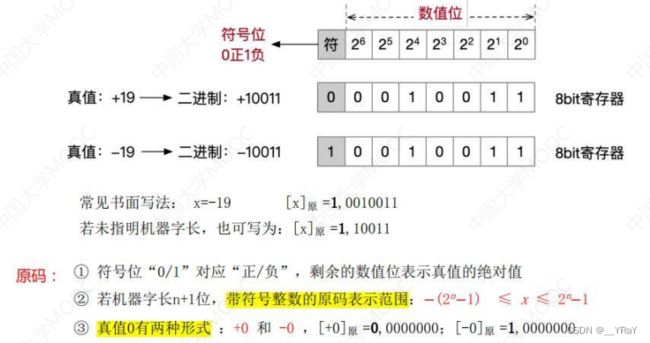
| 带符号整数:原码 | [ -127,127 ] | 0,1111111([+127]原) | 1,1111111([-127]原) | [+0]原:0,0000000 [-0]原:1,0000000 |
| 带符号整数:反码 | [ -127,127 ] | 0,1111111([+127]反) | 1,0000000([-127]反) | [+0]反:0,0000000 [-0]反:1,1111111 |
| 带符号整数:补码 | [ -128,127 ] | 0,1111111([+127]补) | 1,0000000([-128]补) | 0,0000000([0]补) |
| 带符号整数:移码 | [ -128,127 ] | 1,1111111([+127]移) | 0,0000000([-128]移) | 1,0000000([0]移) |
| 无符号整数 | [ 0,255 ] | 11111111(+255) | 00000000(0) | 00000000 |
原码:
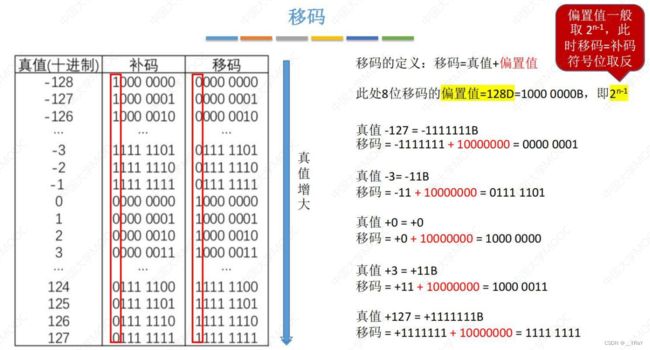
移码:补码的基础上,将符号位取反。只能用于表示整数。
原反补移转换:(注意箭头的单双向 和 全部位?数值位?符号位?的取反)
原反补码特性总结:
考点:(记表格就完事了)
- n+1bit合法表示范围
- 最大最小数的表示
- 真值0的表示
- 两个数A和B进行某种运算后,是否发生溢出? ——手算做题可以带入十进制验证,是否超出合法范围
4.2带符号整数加减法实现原理(补码)
原码的缺点:符号位不能参与运算,需要设计复杂的硬件电路才能处理,费钱!贵!
用补码表示真值——符号位可以参与运算
因此,计算机内部,所有带符号整数的加、减法都要先转化为补码再进行计算
补码加法:从最低位开始,按位相加(符号位参与运算),并往更高位进位
注意补码数值位不能解读为位权
减法: (与无符号整数减法一致,故可以用同一电路实现二者)
①"被减数”不变,“减数”全部位按位取反、末位+1,减法变加法
②从最低位开始,按位相加,并往更高位进位
5.定点小数的表示和运算
5.1定点小数在计算机硬件中如何表示
定点小数原反补转换(与定点整数一致):
定点数的位数拓展的区
![]()
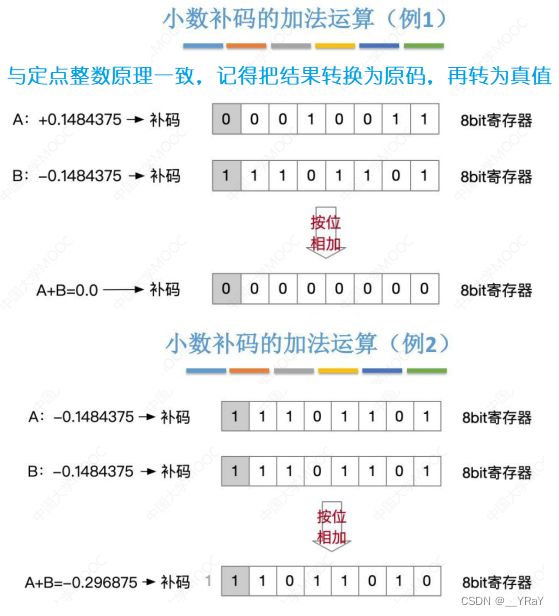
5.2定点小数加减法实现原理
原理与定点整数一致:计算机内部,所有定点小数的加、减法都要先转化为补码再进行计算
补码加法:从最低位开始,按位相加(符号位参与运算),并往更高位进位
补码减法: (与无符号整数/定点整数的减法一致,故可以用同一电路实现二者)
①"被减数”不变,“减数”全部位按位取反、末位+1,减法变加法
②从最低位开始,按位相加,并往更高位进位
6.算术逻辑单元(ALU)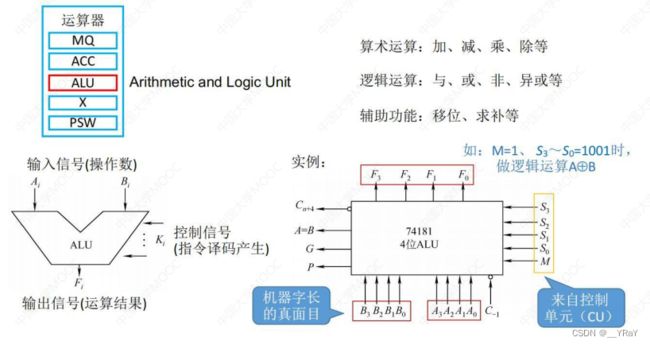
6.1电路的基本原理
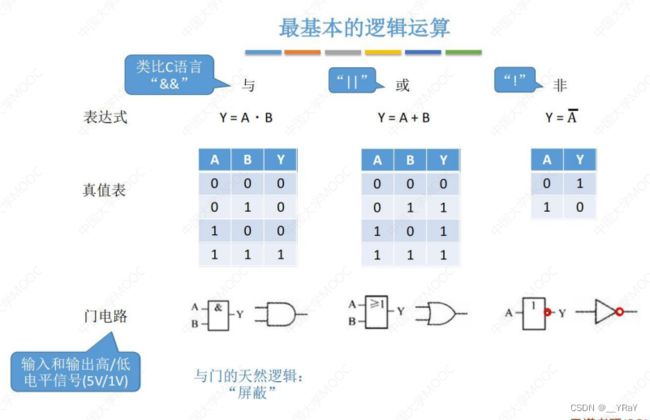
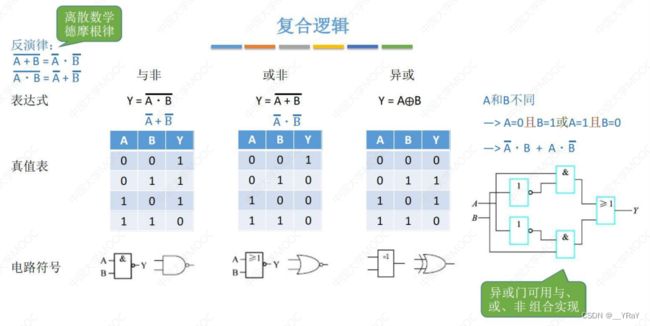
门电路:最基础的逻辑元件,实现逻辑运算。
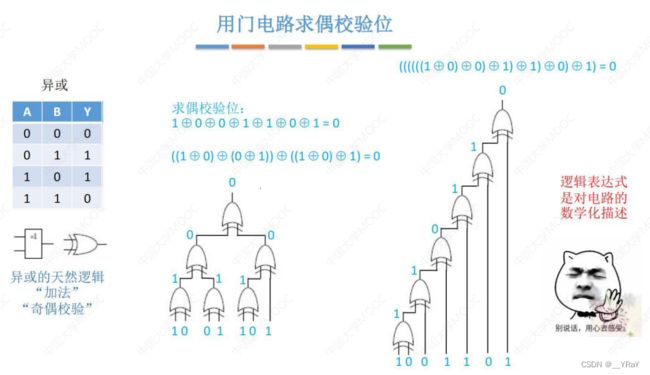
逻辑表达式是对电路的数学化描述
奇偶校验——偶数个1异或得0;奇数个1异或得1
6.2加法器设计
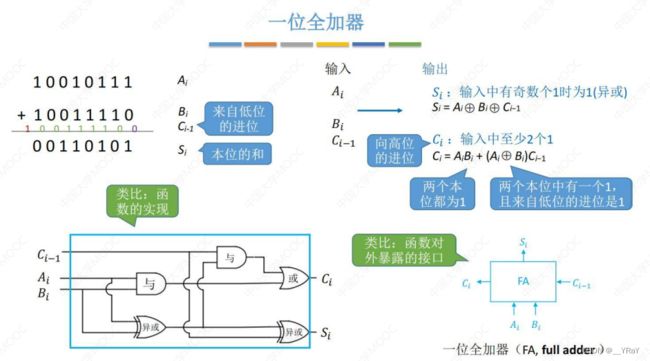
一位全加器:求本为位和(识记Si Ci)
串行加法器 = 一位全加器 + 进位触发器;只能一位一位地加。
并行加法器:多个全加器的简单串联,实现多位同时加,计算速度取决于进位产生和传递的速度。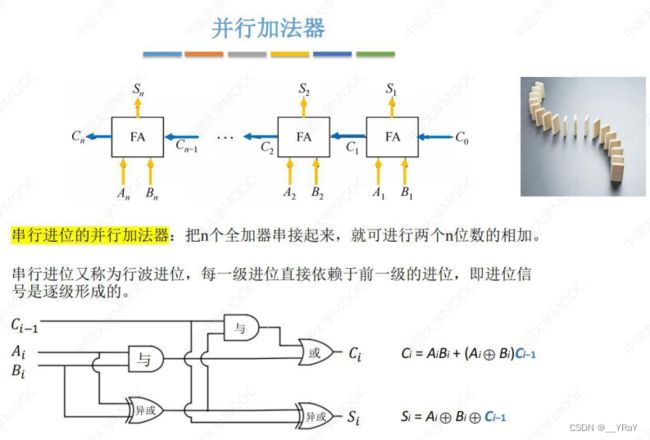
7.并行进位加法器
不是重点~~~
如何更快的产生进位?
8.带符号整数(补码)加减法/无符号整数加减法运算器
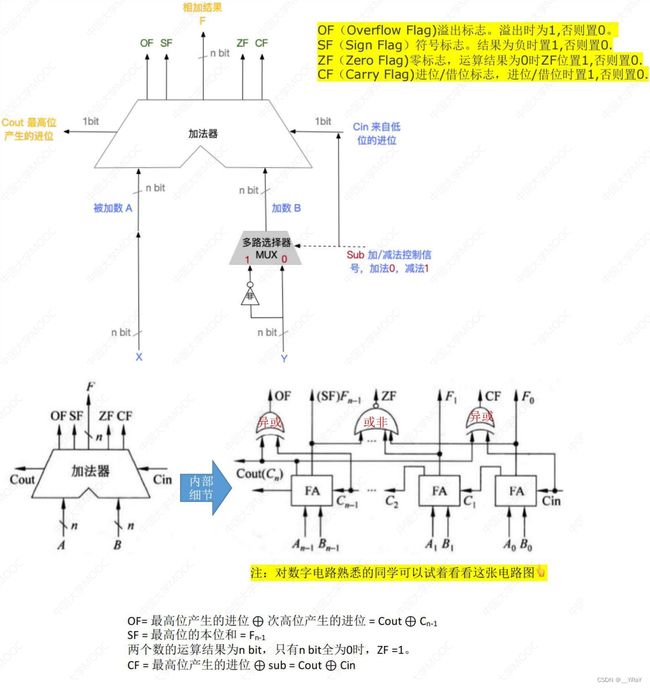
带符号整数(补码)加减法/无符号整数加减法运算器可以用同一电路实现:
9.标志位的生成
 10.定点数的移位运算
10.定点数的移位运算
移位:通过改变各个数码位和小数点的相对位置,从而改变各数码位的位权。可用移位运算实现乘法、除法
10.1算数移位⭐
10.1.1原码的算数移位
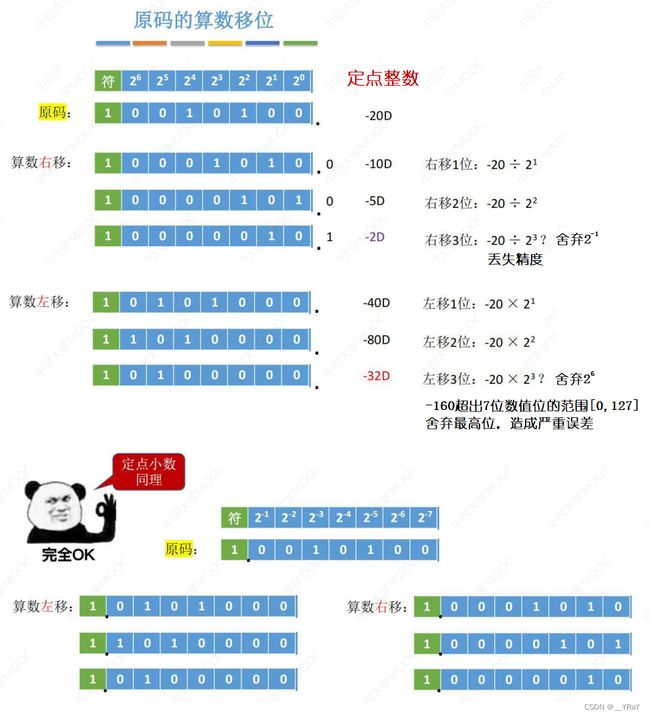
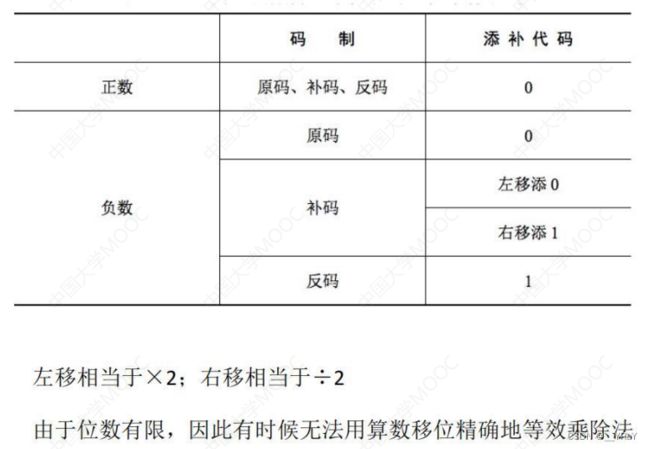
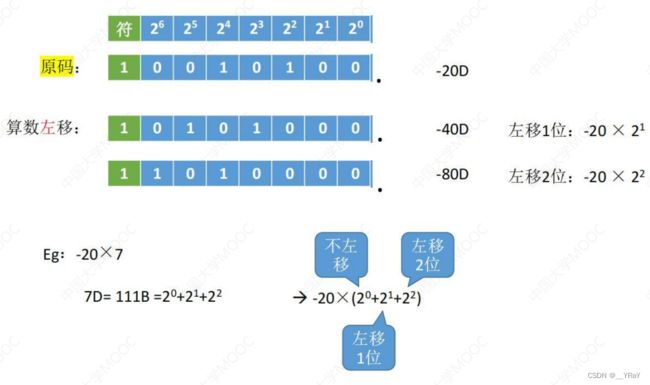
原码的算数移位——符号位保持不变,仅对数值位进行移位。
右移:高位补0,低位舍弃。若舍弃的位=0,则相当于÷2;若舍弃的位≠0,则会丢失精度;
左移:低位补0,高位舍弃。若舍弃的位=0,则相当于×2;若舍弃的位≠0,则会出现严重误差。
10.1.2反码的算数移位
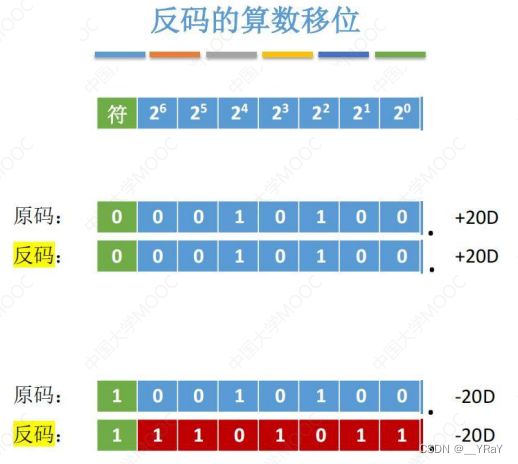
符号位保持不变,仅对数值位进行移位。
正数的反码与原码相同,因此对正数反码的移位运算也和原码相同,移位运算规则如下:
右移:高位补0,低位舍弃。
左移:低位补0,高位舍弃。
负数的反码数值位与原码相反,因此负数反码的移位运算规则如下:
右移:高位补1,低位舍弃。
左移:低位补1,高位舍弃。
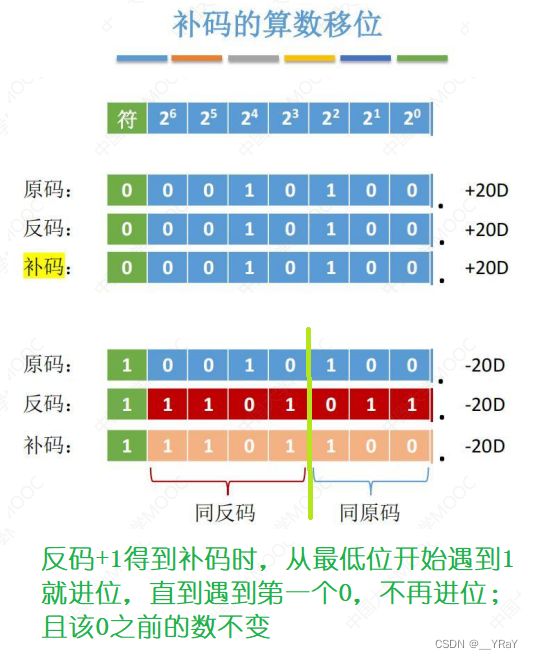
10.1.3补码的算数移位
正数的补码与原码相同,因此对正数补码的移位运算也和原码相同。
右移:高位补0,低位舍弃。
左移:低位补0,高位舍弃。
负数补码=反码末位+1,导致反码最右边几个连续的1都因进位而变为0,直到进位碰到第一个0为止。规律——负数补码中,最右边的1及其右边同原码,最右边的1的左边同反码。负数补码的算数移位规则如下:
右移(同反码) :高位补1,低位舍弃。
左移(同原码) :低位补0,高位舍弃。
小结:
10.1.4应用
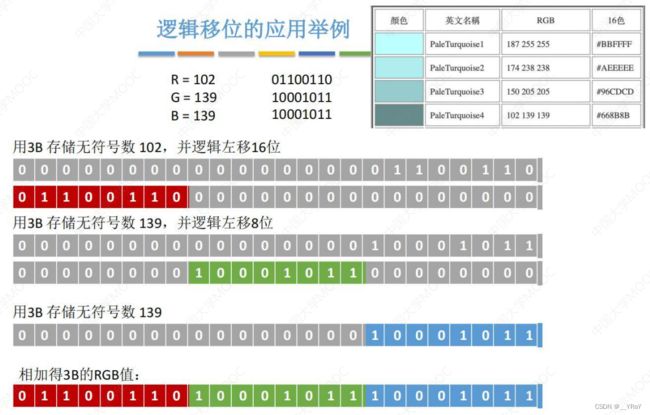
 10.2逻辑移位
10.2逻辑移位
逻辑右移:高位补0,低位舍弃。
逻辑左移:低位补0,高位舍弃。
可以把逻辑移位看作是对“无符号数”的算数移位
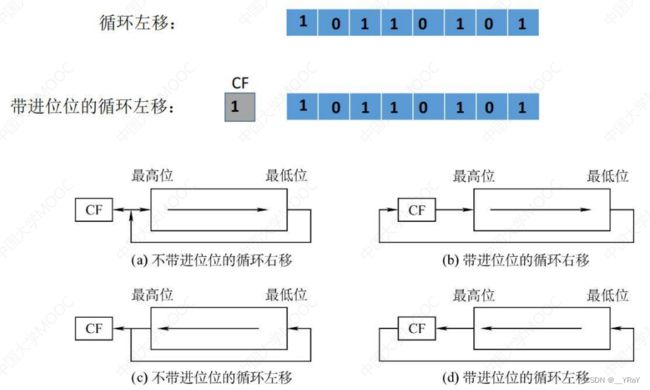
10.3循环移位
不带进位位:用移出的位补上空缺
带进位位:移出的位放到进位位,原进位位补上空缺
进位位CF:实现超过机器字长的数据的加法,要记录低位的进位,再进行高位的相加,而得到正确结果。(存0/1)
应用:把一个数据的高字节和低字节调换
大端存储:先存高位;小端存储:先存低位。通过循环右移/左移实现大端存储和小端存储的转换。
11.乘法运算
11.1原码一位乘法
11.2补码一位乘法
原码一位乘法 VS 补码一位乘法:
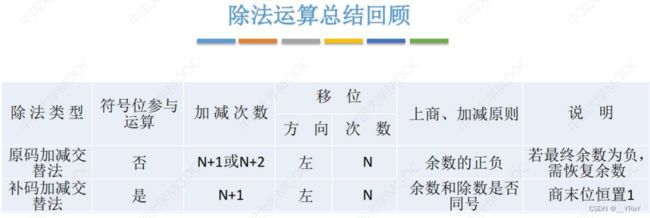
12.除法运算
我们讨论的是定点小数的除法运算,所以商也必为定点小数(0.xxxx)而非整数;因此规定被除数要小于除数,因为若被除数大于除数,则商会>1,定点小数不能表示>1的数。那么硬件如何检查被除数,除数的大小关系?——通过第一步的商来确定,第一步上的商为1时(说明被除数大),硬件电路会检测出该问题,直接停止该除法运算。正常情况下,第一步的余数一定是负数(表示被除数小),而上商0 。
12.1原码除法
12.1.1恢复余数法
12.1.2加减交替法
12.2补码除法
13.C语言类型转换
14.数据的存储和排列
 15.浮点数的表示
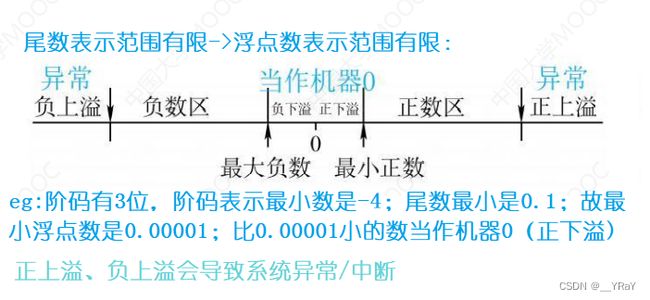
15.浮点数的表示
如何在位数不变的情况下,增加数据表示范围?
 16.IEEE754
16.IEEE754
前面小节都以阶码和尾数都用补码表示
阶码、尾数用什么码表示?各取多少位比较合适?
移码:补码的基础上,符号位取反。用于表示整数
移码的定义:移码 = 真值 + 偏置值;n位移码的偏置值![]()
(如,8位移码偏置值为![]() )
)
1.根据“某浮点数”确定数符、阶码、尾数的分布;
2.确定尾数1.M(注意补充最高的隐含位1);
3.确定阶码的真值=移码-偏置值(可将移码看作无符号数,用无符号数的值减去偏置值);
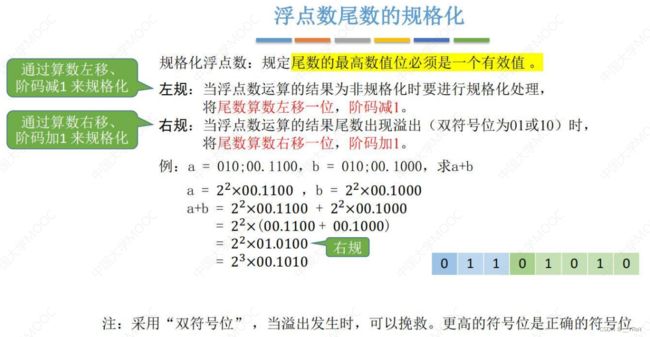
17.浮点数的运算
浮点数加减运算步骤:
1.对阶;2.尾数加减;3.规格化;4.舍入;5.判溢出
课后题补充:
1.可默认BCD码就是8421码
2.使用补码表示时,若符号位相同,则数值位越大码值越大
3.运算器基本功能包括四则运算、逻辑运算以及移位、求补等操作
4.并行进位加法器的两种信号——进位产生信号g(函数):AiBi;进位传递信号p(函数):Ai异或Bi
5.补码定点数加减运算的三种溢出判断方法:
仅当两个符号相同的数相加或两个符号相异的数相减才可能产生溢出。
(1)一位符号位
参与运算的两个数符号相同,但结果与原操作数符号不同,则表示结果溢出
(2)双符号位(模4补码/变形补码)
00、11未溢出;01正溢出,10负溢出
模4补码具有模2补码的全部优点,且更容易检查加减运算中的溢出问题。
只有在ALU中使用双符号位(即只在把两个模4补码的数送往ALU完成加减运算时,才把每个数的符号位同时送入ALU的双符号位中)
(3)一位符号位与最高位进位
符号位进位与最高位进位异或——相同溢出,不同未溢出
6.扩展(符号扩展):无符号整数——0扩展;有符号数——符号扩展
7.char类型(8位无符号整数),转为int时高位补0即可
8.补码一位乘法中,最多n次移位,n+1次加法运算;原码乘法移位和加减运算最多均为n次;原码不恢复余数法(加减交替法),只在最终余数为负时,才需要恢复余数,故最终可能多加一次,因此原码不恢复余数法最多n+2次加减
9.补码表示时,正数符号位为0,左移最高位为0时,数据不会丢失;负数符号位为1,左移最高位为1时,数据不会丢失;因此为保证数据不丢失,每次左移移走的最高位都需与符号位保持一致
10.基数不同,浮点数规格化形式也不同。r=2,原码规格化数的尾数最高位一定是1;r=4,原码规格化数的尾数最高两位不全为0
11.IEEE754标准:阶码用移码表示;尾数用带隐藏位策略的原码表示
12.char->int->long->double;float->double:从前到后范围和精度从小到大,转换过程没有损失。不同类型的数据混合运算时,遵循的原则是“类型提升”(较低类型转为较高类型),由系统自动转换(隐式转换)