蓝桥杯 基础练习 完美的代价Python实现（贪心算法）

问题描述
　　回文串，是一种特殊的字符串，它从左往右读和从右往左读是一样的。小龙龙认为回文串才是完美的。现在给你一个串，它不一定是回文的，请你计算最少的交换次数使得该串变成一个完美的回文串。
　　交换的定义是：交换两个相邻的字符
　　例如mamad
　　第一次交换 ad : mamda
　　第二次交换 md : madma
　　第三次交换 ma : madam (回文！完美！)
输入格式
　　第一行是一个整数N，表示接下来的字符串的长度(N <= 8000)
　　第二行是一个字符串，长度为N.只包含小写字母
输出格式
　　如果可能，输出最少的交换次数。
　　否则输出Impossible
样例输入
5
mamad
样例输出
3

分析：

题目给的关键字是贪心算法，贪心算法关键是要找到贪心策略。对于我们这题来说，要做的事情有两件：①先判断这个字符串能不能够经过交换变成‘完美的回文字符串’，②是每一步都使用贪心策略。

1. 判断:
   对于字符串长度是偶数的字符串，每个字符的数目都是偶数，一旦出现奇数，则输出impossible。
   对于字符串长度是奇数的字符串，只能有一个字符的数目是奇数，一旦出现两个，则输出impossible。
   判断实现比较简单，注意减少代码复杂度（题给字符串长度范围是8000，很容易运行超时）
2. 贪心策略:
   对于偶数的字符串，我们从第一个开始遍历，再倒序遍历出同样的，这个倒序遍历出来的序号，就是该移动的步数。我们把这个步数加到总步数之后，用pop弹出这个值。进行第二轮遍历。
   遍历用n/2做大循环，用另一个序列做倒序序列，倒序序列更新后，原来的序列也要更新。
   

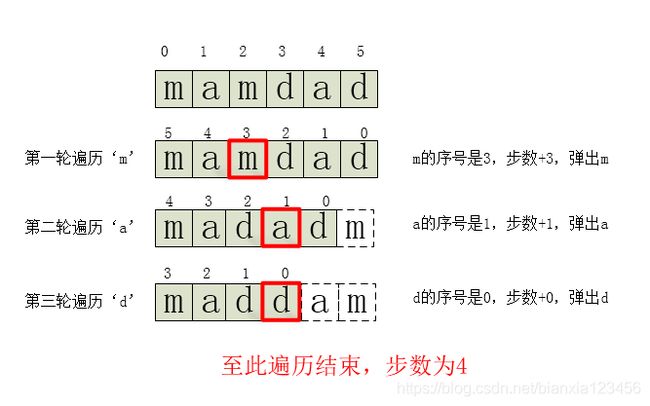
对于奇数的字符串，其实贪心策略和偶数的时候一样，只不过我们一直遍历下去会有一个字符没有匹配，那么这个字符肯定是放在中间的，我们设置一个判断，假如剩余的该字符个数不是1，按照和偶数一样的遍历，如果该字符是1，直接移动到最中间的位置。

AC代码：

while True:
    try:
        def huiwen(n, s):  # 判断能不能组成回文数
            temp = set()
            if n % 2 == 0:
                for i in range(26):
                    if s.count(chr(ord('a') + i)) % 2 != 0:  # 如果某个字符不是偶数个
                        print('Impossible')
                        return False
                else:
                    return True

            else:
                for j in range(26):
                    if s.count(chr(ord('a') + j)) % 2 != 0:
                        temp.add(chr(ord('a') + j))  # 把个数是奇数个的字符放进temp
                    if len(temp) > 1:
                        print('Impossible')
                        return False
                else:
                    return True


        def step(n, s, s1, res):
            for i in range(n // 2):
                if s[i:].count(s[i]) != 1:
                    temp = s1[:n - i].index(s[i])  # 是要移动的步数
                    s1.pop(temp)
                    res += temp
                    s = s1[::-1]
                else:
                    res += n // 2 - i
                    s[i] = None
                    s1 = s[::-1]
            return res


        n = int(input())
        s = list(input())
        s1 = s[::-1]
        res = 0
        if huiwen(n, s):
            print(step(n, s, s1, res))
    except:
        break

编程小白记录成长