机器学习六—深度学习算法之人工神经网络(ANN)
人工神经网络(ANN)
- 一、什么是人工神经网络
- 二、人工神经网络的运行原理
- 三、神经网络训练过程
- 四、神经网络 MLPClassifier 参数用法
- 五、人工神经网络算法实现
-
- 1.首先简单使用sklearn中的neural_network的例子
- 2.用神经网络训练iris数据集
- 3.用神经网络训练MNIST数据集并实现分类
- 总结
一、什么是人工神经网络
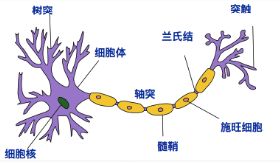
人工神经网络的灵感来自其生物学对应物。生物神经网络使大脑能够以复杂的方式处理大量信息。大脑的生物神经网络由大约1000亿个神经元组成,这是大脑的基本处理单元。神经元通过彼此之间巨大的连接(称为突触)来执行其功能。
- 接收区(receptive zone):树突接收到输入信息。
- 触发区(trigger zone):位于轴突和细胞体交接的地方,决定是否产生神经冲动。
- 传导区(conducting zone):由轴突进行神经冲动的传递。
- 输出区(output zone):神经冲动的目的就是要让神经末梢,突触的神经递质或电力释出,才能影响下一个接受的细胞(神经元、肌肉细胞或是腺体细胞),此称为突触传递。
人工神经网络定义为:人工神经网络是一种由具有自适应性的简单单元构成的广泛并行互联的网络,它的组织结构能够模拟生物神经系统对真实世界所做出的交互反应。
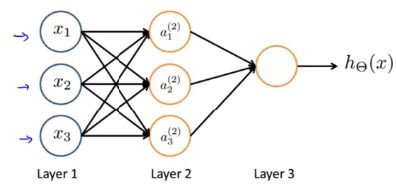
- 输入层:输入层接收特征向量 x 。
- 输出层:输出层产出最终的预测 h 。
- 隐含层:隐含层介于输入层与输出层之间,之所以称之为隐含层,是因为当中产生的值并不像输入层使用的样本矩阵 X 或者输出层用到的标签矩阵 y 那样直接可见。
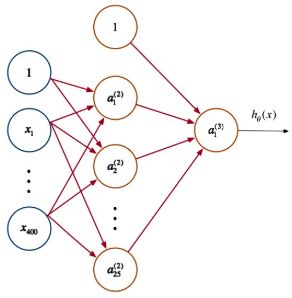
- 人工神经网络由一个输入层和一个输出层组成,其中输入层从外部源(数据文件,图像,硬件传感器等)接收数据,一个或多个隐藏层处理数据,输出层提供一个或多个数据点基于网络的功能。根据不同的问题,可以加入多个隐藏层,由图中这种全连接改为部 分连接,甚至是环形连接等。
二、人工神经网络的运行原理
人工神经网络的强大之处在于,它拥有很强的学习能力。在得到一个训练集之后,它能通过学习提取所观察事物的各个部分的特征,将特征之间用不同网络节点连接,通过训练连接的网络权重,改变每一个连接的强度,直到顶层的输出得到正确的答案。
神经网络算法大致过程:
- 第一步,我们要预先设定一种网络结构和激活函数, 这一步其实很困难,因为网络结构可以无限拓展,要知道什么样的结构才符合我们的问题需要做大量的试验。
- 第二步,初始化模型中的权重。 模型中的每一个连接都会有一个权重,在初始化的时候可以都随机给予一个值。
- 第三步,就是根据输入数据和权重来预测结果。 由于最开始的参数都是随机设置的,所以获得的结果肯定与真实的结果差距比较大,所以在这里要计算一个误差,误差反映了预测结果和真实结果的差距有多大。
- 最后一步,模型要调节权重 。这里我们可以参与的就是需要设置一个 “学习率”,这个学习率是针对误差的,每次获得误差后,连接上的权重都会按照误差的这个比率来进行调整,从而期望在下次计算时获得一个较小的误差。经过若干次循环这个过程,我们可以选择达到一个比较低的损失值的时候停止并输出模型,也可以选择一个确定的循环轮次来结束。
神经网络每层都包含有若干神经元,层间的神经元通过权值矩阵 Θl 连接。一次信息传递过程可以如下描述:
第 j 层神经元接收上层传入的刺激(神经冲动):
该激活函数(activation function)g 作用后,会产生一个激活向量 aj 。 aji 表示的就是 j 层第 i
个神经元获得的激活值(activation):
人工神经网络算法主要是前向传播: 刺激由前一层传向下一层,故而称之为前向传递。
对于非线性分类问题,逻辑回归会使用多项式扩展特征,导致维度巨大的特征向量出现,而在神经网络中,并不会增加特征的维度,不是扩展神经网络输入层的规模,而是通过增加隐含层,调节隐含层中的权值,从而不断优化特征,前向传播过程每次在神经元上产出的激励值都可看做是优化后的特征。
代价函数
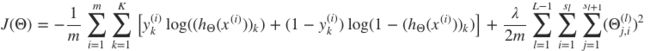

矩阵表示方法为:
![]()
其中, .∗ 代表点乘操作,A∈R(K×m) 为所有样本对应的输出矩阵,其每一列对应一个样本的输出, Y∈R(m×K) 为标签矩阵,其每行对应一个样本的类型。
三、神经网络训练过程
参考:https://zhuanlan.zhihu.com/p/111288383
人工神经网络首先为神经元之间的连接权重分配随机值。ANN正确而准确地执行其任务的关键是将这些权重调整为正确的数字。 但是找到合适的权重并不是一件容易的事,特别是处理多层和成千上万的神经元时。
通过对带有注释示例的网络进行“培训”来完成此校准。基本上,训练期间发生的事情是网络进行自我调整以从数据中收集特定模式。同样,对于图像分类器网络,当您使用质量示例训练AI模型时,每一层都会检测到特定的特征类别。例如,第一层可能检测到水平和垂直边缘,第二层可能检测到拐角和圆形。在网络的更深处,更深的层次将开始挑选出更高级的功能,例如面部和物体。
神经网络的每一层都将从输入图像中提取特定特征。
当您通过训练有素的神经网络运行新图像时,调整后的神经元权重将能够提取正确的特征并准确确定图像属于哪个输出类别。
训练神经网络的挑战之一是找到正确数量和质量的训练示例。而且,训练大型AI模型需要大量的计算资源。为了克服这一挑战,许多工程师使用“ 转移学习”(一种培训技术),您可以采用预先训练的模型,并使用针对特定领域的新示例对其进行微调。当已经有一个与您的用例接近的AI模型时,转移学习特别有效。
四、神经网络 MLPClassifier 参数用法
clf = MLPClassifier(solver=’sgd’, activation=’relu’,alpha=1e-4,
hidden_layer_sizes=(50,50), random_state=1,
max_iter=10,verbose=10,learning_rate_init=.1)
参数说明:
- hidden_layer_sizes :例如hidden_layer_sizes=(50, 50),表示有两层隐藏层,第一层隐藏层有50个神经元,第二层也有50个神经元。
- activation :{‘identity’, ‘logistic’, ‘tanh’, ‘relu’}, 默认‘relu
- identity: no-op activation, useful to implement linear bottleneck, 返回f(x) = x
- logistic:the logistic sigmoid function, returns f(x) = 1 / (1 + exp(-x)).
- tanh:the hyperbolic tan function, returns f(x) = tanh(x).
- relu:the rectified linear unit function, returns f(x) = max(0, x)
- solver: {‘lbfgs’, ‘sgd’, ‘adam’}, 默认adam,用来优化权重
- lbfgs:quasi-Newton方法的优化器
- sgd:随机梯度下降
- adam: Kingma, Diederik, and Jimmy Ba提出的机遇随机梯度的优化器 注意:默认solver ‘adam’在相对较大的数据集上效果比较好(几千个样本或者更多),对小数据集来说,lbfgs收敛更快效果也更好。
- alpha :float,可选的,默认0.0001,正则化项参数。
- learning_rate :学习率,用于权重更新,只有当solver为’sgd’时使用,{‘constant’,’invscaling’, ‘adaptive’},默认constant
- constant: 有’learning_rate_init’给定的恒定学习率
- incscaling:随着时间t使用’power_t’的逆标度指数不断降低学习率learning_rate_ ,effective_learning_rate = learning_rate_init / pow(t, power_t)
- adaptive:只要训练损耗在下降,就保持学习率为’learning_rate_init’不变,当连续两次不能降低训练损耗或验证分数停止升高至少tol时,将当前学习率除以5.
- random_state:int 或RandomState,可选,默认None,随机数生成器的状态或种子。
- max_iter: int,可选,默认200,最大迭代次数。
- verbose : bool, 可选, 默认False,是否将过程打印到stdout。
五、人工神经网络算法实现
属性说明:
- classes_:每个输出的类标签
- loss_:损失函数计算出来的当前损失值
- coefs_:列表中的第i个元素表示i层的权重矩阵
- intercepts_:列表中第i个元素代表i+1层的偏差向量
- n_iter_ :迭代次数
- n_layers_:层数
- n_outputs_:输出的个数
- out_activation_:输出激活函数的名称。
1.首先简单使用sklearn中的neural_network的例子
- 实例1
from sklearn.neural_network import MLPClassifier
X = [[0., 0.], [1., 1.]]
y = [0, 1]
mlp = MLPClassifier(solver='lbfgs', alpha=1e-5,hidden_layer_sizes=(5, 5), random_state=1)
mlp.fit(X, y)
print(mlp.n_layers_) # n_layers_:层数
print(mlp.n_iter_) # n_iter_ :迭代次数
print(mlp.loss_) # loss_:损失函数计算出来的当前损失值
print(mlp.out_activation_)# out_activation_:输出激活函数的名称。
输出为:
4
13
0.00014123347253650121
logistic
2.用神经网络训练iris数据集
- 实例2
from sklearn import datasets
import numpy as np
from sklearn.neural_network import MLPClassifier
np.random.seed(0)
iris=datasets.load_iris()
iris_x=iris.data
iris_y=iris.target
indices = np.random.permutation(len(iris_x))
# 训练数据集
iris_x_train = iris_x[indices[:-10]]
iris_y_train = iris_y[indices[:-10]]
# 测试训练集
iris_x_test = iris_x[indices[-10:]]
iris_y_test = iris_y[indices[-10:]]
# 建立神经网络模型
clf = MLPClassifier(solver='lbfgs', alpha=1e-5,
hidden_layer_sizes=(10, 10, 10), random_state=1)
# 调用fit函数就可以进行模型训练,一般的调用模型函数的训练方法都是fit()
clf.fit(iris_x_train,iris_y_train)# 训练
iris_y_predict = clf.predict(iris_x_test)# 预测
#score=clf.score(iris_x_test,iris_y_test,sample_weight=None)
#print('Accuracy:',score)
print('iris_y_predict = ')
print(iris_y_predict)
print('iris_y_test = ')
print(iris_y_test)
# print(iris_x_train.shape)
# print(iris_y_train.ravel().shape)
# 模型就这样训练好了,而后我们可以调用多种函数来获取训练好的参数
# 比如获取准确率
print('训练集的准确率是:', clf.score(iris_x_test, iris_y_test.ravel()))
# 比如输出当前的代价值
print('训练集的代价值是:', clf.loss_)
# 比如输出每个0的权重
print('训练集的权重值是:', clf.coefs_)
输出为:
iris_y_predict =
[1 2 1 0 0 0 2 1 2 0]
iris_y_test =
[1 1 1 0 0 0 2 1 2 0]
训练集的准确率是: 0.9
训练集的代价值是: 0.028961695000958302
训练集的权重值是: [array([[-5.34765782, 5.02607209, -0.65445869, -0.93203818, -0.46247314,
-0.53371718, -0.41075342, -0.2021945 , -0.13515376, 3.88121192],
[-2.58847781, 2.24422541, -0.3869361 , 0.11961756, -0.61875213,
0.22317894, -0.10826595, 0.07683771, -0.47081148, 2.26559598],
[-3.42989695, -3.81805074, -0.24426821, -0.13840658, 0.49277502,
0.5166257 , -0.54326711, -0.60347725, -0.43226358, 4.69691872],
[-1.80024637, -4.38159899, 0.59947669, -0.07771922, 0.25120875,
-0.24153005, 0.24417016, 0.43809757, -0.63066511, 2.40462441]]), array([[-5.26470733e-01, 1.49390693e-01, -3.41933505e-01,
-2.56813018e-01, -9.23050356e-03, -9.93090514e-02,
1.09631267e-01, -4.56749569e-01, -1.45487465e+00,
1.89549936e-01],
[-4.35590703e-01, -7.30266967e+00, 5.34189927e+00,
-9.40054030e-02, -4.92967215e-01, 1.23750423e-01,
4.42863519e+00, 3.93362772e-01, -1.35109666e+01,
5.69772279e+00],
[ 4.41874119e-01, -3.97099120e-01, -3.95125655e-01,
3.36707015e-01, -1.12081663e-01, -3.66560776e-01,
4.68279822e-01, -1.66752621e-01, 2.74731906e-01,
2.47551280e-01],
[ 4.19861768e-01, 6.30701626e-02, 1.22965600e-01,
-1.65512134e-01, -2.52013950e-01, 6.14180831e-01,
-6.51501916e-02, 2.84518575e-01, -1.15104525e-01,
-1.48918308e-03],
[-4.21995477e-01, 4.92356785e-01, -5.48647169e-02,
8.58655858e-02, -1.00624136e-01, -2.88052602e-01,
4.41849588e-01, 8.07062560e-02, -5.44540637e-01,
1.28316955e-01],
[-1.89887872e-01, 2.96386176e-02, 4.22749170e-01,
-1.56342339e-01, 4.47496908e-01, 1.35124897e-01,
-5.30354600e-01, 4.70392410e-01, 2.09102644e-01,
5.44752238e-01],
[-3.58908185e-01, -3.97470400e-01, 4.73851838e-01,
2.15588594e-01, -4.75390135e-01, 2.79826414e-01,
2.78088211e-01, 4.63368137e-01, 2.31697750e-01,
-4.11562095e-01],
[-5.25908615e-01, -5.18973993e-01, -5.16678645e-01,
-2.77992634e-01, 3.94363602e-01, 4.25343601e-02,
5.78595797e-02, 3.74650177e-01, -4.11669055e-01,
-2.41875444e-01],
[ 9.39380827e-02, 5.14380819e-01, 6.68506354e-02,
-5.27259035e-01, 3.29303834e-01, -2.92491813e-01,
3.36393637e-01, -1.22834020e-01, 3.98212627e-01,
2.70689488e-01],
[ 6.16038320e-02, -3.97855478e-01, -1.27257989e+00,
-4.14768796e-01, -4.98883941e-01, -5.96496512e-01,
-3.19331697e+00, 2.12507568e+00, -8.41029680e+00,
-1.76799741e+00]]), array([[-0.28496281, -0.00682446, 0.13139582, 0.36035561, -0.37594021,
-0.5273369 , -0.47098459, -0.01495715, 0.11647004, 0.07541776],
[-0.20005563, -0.61622957, -0.40422466, -0.13128969, 1.85753807,
1.32940591, 0.18537253, 1.01481888, 0.04705743, -0.22216349],
[ 1.00177309, -2.06268541, 1.05575279, -0.47536612, 1.41319718,
1.45462143, -0.3368449 , 0.58103227, -1.24279971, 0.21891478],
[-0.25927748, -0.47543294, 0.25748407, 0.29813549, 0.44670901,
0.47316899, -0.53240258, -0.29097165, 0.12791544, 0.49183874],
[ 0.49310915, 0.06205617, 0.45524248, 0.1550673 , -0.12048219,
-0.01534539, 0.11425851, 0.05427328, 0.4668261 , 0.4586678 ],
[-0.2901463 , -1.07333798, -0.1081764 , -0.3741978 , 1.67270343,
0.09116315, -0.52605417, 3.12164114, -0.59659312, -0.70768536],
[-0.36454908, -0.40257552, -0.51276662, 0.34133008, -0.33176354,
0.94989301, 0.08983582, 1.00903272, 0.08271108, 0.2491274 ],
[ 0.01355157, -1.32627346, 0.37706837, -0.21984049, 1.03260505,
0.1302209 , -0.5313403 , 0.21814048, -3.64239047, 0.20238919],
[ 1.9602507 , 3.03073636, 3.05337344, -0.34519025, -4.71177394,
-2.88572976, -0.48863414, -0.79067751, -1.3144379 , -0.84814611],
[-1.7043494 , -1.74966892, -2.55520768, 0.5187887 , 2.20925683,
2.99660261, 0.0818367 , 5.39000439, 0.79490188, 0.38422736]]), array([[-2.20767764, 0.60719605, 1.3841631 ],
[ 0.8890124 , 1.83522321, -1.93371145],
[-4.32763728, 1.07943945, 2.52624059],
[ 0.36571678, 0.50478852, 0.59883383],
[-7.1122914 , 3.04341732, 3.64130343],
[ 4.64457226, -1.84380095, -1.8704114 ],
[ 0.08064337, 0.31698989, 0.04343878],
[ 4.5665846 , 0.88728985, -5.03887589],
[-2.76421032, 2.06166158, -0.26368451],
[-0.28865365, -0.54975289, 0.49067121]])]
3.用神经网络训练MNIST数据集并实现分类
MNIST(手写数字)数据集的下载:http://www.iro.umontreal.ca/~lisa/deep/data/mnist/mnist.pkl.gz
- 实例3
from sklearn.neural_network import MLPClassifier
import numpy as np
import pickle
import gzip
# 加载数据
# mnist = fetch_mldata("MNIST original")
with gzip.open("mnist.pkl.gz") as fp: # 打开压缩包
training_data, valid_data, test_data = pickle.load(fp, encoding='bytes')
x_training_data, y_training_data = training_data
x_valid_data, y_valid_data = valid_data
x_test_data, y_test_data = test_data
classes = np.unique(y_test_data)
# 将验证集和训练集合并
x_training_data_final = np.vstack((x_training_data, x_valid_data))
y_training_data_final = np.append(y_training_data, y_valid_data)
# 设置神经网络模型参数
# mlp = MLPClassifier(solver='lbfgs', activation='relu',alpha=1e-4,hidden_layer_sizes=(50,50), random_state=1,max_iter=10,verbose=10,learning_rate_init=.1)
# 使用solver='lbfgs',准确率为79%,比较适合小(少于几千)数据集来说,且使用的是全训练集训练,比较消耗内存
# mlp = MLPClassifier(solver='adam', activation='relu',alpha=1e-4,hidden_layer_sizes=(50,50), random_state=1,max_iter=10,verbose=10,learning_rate_init=.1)
# 使用solver='adam',准确率只有67%
mlp = MLPClassifier(solver='sgd', activation='relu', alpha=1e-4, hidden_layer_sizes=(50, 50), random_state=1,
max_iter=100, verbose=True, learning_rate_init=.1)
# 使用solver='sgd',准确率为98%,且每次训练都会分batch,消耗更小的内存
# 训练模型
mlp.fit(x_training_data_final, y_training_data_final)
# 查看模型结果
print('训练集的准确率是:', mlp.score(x_test_data, y_test_data))
print('训练集的层数为:', mlp.n_layers_)
print('训练集的迭代次数', mlp.n_iter_)
print('训练集的代价值是:', mlp.loss_)
print('输出激活函数的名称', mlp.out_activation_)
输出为:
Iteration 1, loss = 0.31443422
Iteration 2, loss = 0.13076474
Iteration 3, loss = 0.09742518
Iteration 4, loss = 0.08100330
Iteration 5, loss = 0.06801913
Iteration 6, loss = 0.06219844
Iteration 7, loss = 0.05419017
Iteration 8, loss = 0.04854781
Iteration 9, loss = 0.04317298
Iteration 10, loss = 0.03969231
Iteration 11, loss = 0.03611715
Iteration 12, loss = 0.03517457
Iteration 13, loss = 0.03175764
Iteration 14, loss = 0.02452196
Iteration 15, loss = 0.02415626
Iteration 16, loss = 0.02818433
Iteration 17, loss = 0.02416141
Iteration 18, loss = 0.02778512
Iteration 19, loss = 0.02067801
Iteration 20, loss = 0.01823760
Iteration 21, loss = 0.01707471
Iteration 22, loss = 0.01857857
Iteration 23, loss = 0.01804544
Iteration 24, loss = 0.01649068
Iteration 25, loss = 0.02124260
Iteration 26, loss = 0.01870442
Iteration 27, loss = 0.01621165
Iteration 28, loss = 0.01799651
Iteration 29, loss = 0.02138072
Iteration 30, loss = 0.02465049
Iteration 31, loss = 0.02191574
Iteration 32, loss = 0.01599686
Iteration 33, loss = 0.01287339
Iteration 34, loss = 0.00995048
Iteration 35, loss = 0.01650707
Iteration 36, loss = 0.01554510
Iteration 37, loss = 0.01805111
Iteration 38, loss = 0.01707025
Iteration 39, loss = 0.01888330
Iteration 40, loss = 0.01726329
Iteration 41, loss = 0.01413027
Iteration 42, loss = 0.01359649
Iteration 43, loss = 0.01395890
Iteration 44, loss = 0.01488300
Iteration 45, loss = 0.01299176
Training loss did not improve more than tol=0.000100 for 10 consecutive epochs. Stopping.
训练集的准确率是: 0.9732
训练集的层数为: 4
训练集的迭代次数 45
训练集的代价值是: 0.012991756948993145
输出激活函数的名称 softmax
总结
分析实例1、实例2和实例3:
对于神经网络的输出层(即mlp.out_activation_且不可设置),激活函数的选取还是有一定的原则的:
- 如果是两类判别,输出层只有一个神经元,那么选logistic,即实例1mlp.out_activation_输出;
- 如果是n类判别,输出层有n个神经元,那么选softmax即实例2和实例3,输出0-9多分类;
- 如果是回归,那么选线性。
这些选择并不是为了提高性能,而只是让输出的范围合理。
对于判别问题,输出是概率,所以必须在0到1之间,多类判别时还需要加起来等于1;
对于回归问题,一般没有理由要求输出在0到1之间。
神经网络的好处和局限性
- 人工神经网络的特点和优越性:
- 具有自学习功能 。
- 具有联想存储功能 。
- 具有高速寻找优化解的能力。
- 局限性:
- 神经网络需要大量数据,非常消耗资源,开销也非常大的,而且训练时间长,还需要耗费很大的人力物力。
- 神经网络在概括方面很不好。
- 神经网络是不透明的。