堆-topK问题-堆排序-优先级队列的对象比较问题
堆-topK问题-堆排序
堆(heap)的概念❓
- 以孩子表示法(刷题常见表示法)去表示一颗二叉树,其本质是一种链式存储,那对二叉树的存储,其实还有一种顺序存储,说白了就是拿一个数组去存储一个二叉树,填数组(从0下标开始填)方式是层序遍历
- 当以层序遍历一棵完全二叉树时,并将遍历到的数据放到数组当中时,并且这棵二叉树的某个节点的值总是不大于或者不小于父节点的值,那这棵二叉树就是一个堆
性质
- 把整棵树的根的下标定为0,那对于完全二叉树:一个节点的下标是i,如果这个节点有双亲,那这个节点的双亲的下标就是(i-1)/2
- 完全二叉树中,如果双亲节点的下标是i,如果这个节点有孩子,那左孩子的下标就是2*i+1,右孩子的下标就是:2 *i+2
- 堆物理上存于数组当中,逻辑上是一棵二叉树
- 若一棵完全二叉树的所有根都大于这个根左右孩子节点的值,那这棵树就是一个大根堆,反之是一个小根堆
- 堆的基本作用就是找最值
- 堆在数据框架中就是优先级队列:PriorityQueue
如何将一个数组建成一个堆
- 本质是对一个数组进行操作,使得遵循规则的下标处的元素要符合一定的要求,那就建堆完成
- 堆无非两种,大根堆和小根堆,这决定了在每棵二叉树中孩子较大才与双亲进行交换位置,还是较小才与双亲交换位置;如建立一个大根堆:我们可以以最大下标作为整棵树的最后一个孩子,那这个孩子的双亲下标依据性质1可得到,因为是建立大根堆,将两个孩子的较大者与双亲进行比较,若较大者比双亲还大,则交换双亲和较大的孩子的位置;当一个堆搭建到上面的时候,此时的孩子,将作为下一层的双亲,若不满足双亲大于孩子,那就会使得已经搭建起来的底部二叉树不再符合堆的性质,所以要加一个向下检测的步骤。代码:
public class TestDemo {
/*
向下调整函数,parent为待调整的树根,len为迭代终止条件
*/
private static void shiftDown(int[] array,int parent,int len){
int child=2*parent+1;//必存在,因为实参是依据孩子找的双亲
while(child<len){
if(child+1<len&&array[child]<array[child+1]){
child++;//找两个孩子的较大者
}
if(array[parent]<array[child]){
swap(array,parent,child);
//交换完就要向下检测
parent=child;
child=2*parent+1;
}else{
break;//我们是从下面往上面搭建的
}
}
}
private static void swap(int[] array,int i,int j){
int tmp=array[i];
array[i]=array[j];
array[j]=tmp;
}
private static void createBigHeap(int[] array){
for(int parent=(array.length-1-1)/2;parent>=0;parent--){
shiftDown(array,parent,array.length);
}
}
public static void main(String[] args) {
int[] array={1,2,3,4,5,6,7,8,9,10};
createBigHeap(array);
System.out.println("========");
}
}
//建堆前:1 2 3 4 5 6 7 8 9 10
//建堆后:10 9 7 8 5 6 3 1 4 2 (层序遍历的方式还原成一个二叉树,发现确实是一个大根堆)
分析一下建堆的时间复杂度
就考虑最差的情况:如上述代码中的升序数组
以层序遍历的方式将其还原成一棵二叉树,可以发现是一个小根堆,当每次研究一个parent时,会发现都要进行向下调整,即把当前的parent下标处的元素调整到最底层,直至parent=0做完为止;假设整棵树的高度是k,则从第k-1层开始的每一个节点都将被调整至最底层,可以简单看出,第k-1层的每个节点需进行向下调整1次,k-2层的每个节点需要向下调整2次,依次类推:可得shiftDown()执行的次数:
T(N)=2^0 *(K-1)+2^1 *(K-2)+…+2^(K-2) *1
使用错位相减法,可以得到T(N)=2^k-k-1
又因为:深度为k的满二叉树:节点总数为:2^k -1个,推得树高和节点数的关系:k=log(n+1)此处的log都是以2为底
则:O(n)=2^(log(n+1))-log(n+1)-1=n-log(n+1),显然后者不是与前者一个量级,即O(n)为时间复杂度
往建完堆的数组中,新增一个元素,如何保证整体还是一个堆?
如果是建立的一个大根堆,以数组元素个数为下标处填新增元素,保证整体仍然是一个堆的本质就是确定这个新增的元素应当放到哪里,再究其本质就是看它能爬多高?见代码:
private static void shiftUp(int[] tmp,int child){
int parent=(child-1)/2;
while(child>0){
if(tmp[child]>tmp[parent]){
swap(tmp,child,parent);
child=parent;
parent=(child-1)/2;
}else{
break;//能爬多高爬多高
}
}
}
private static int[] offer(int[] array,int data){
int[] tmp=new int[array.length+1];
for(int i=0;i<array.length;i++){
tmp[i]=array[i];
}
tmp[array.length]=data;
shiftUp(tmp,tmp.length-1);
return tmp;
}
public static void main(String[] args) {
int[] array={1,2,3,4,5,6,7,8,9,10};
createBigHeap(array);
int[] ret=offer(array,99);
System.out.println("========");
}
将堆顶元素删除如何保证整体还是一个堆
private static int poll(int[] array){
//先将首尾元素互换,再将0这课树做向下调整
int tmp=array[0];
swap(array,0,array.length-1);
shiftDown(array,0,array.length-1);
return tmp;
}
topK问题
-
思路一:给整体排序,然后取前k个元素即可,比如使用时间复杂度为O(n^2)的冒泡排序
-
思路二:如果要求前k个最大值,则建立一个小根堆,从k+1个元素开始往后遍历,依次将这些个元素和堆顶元素进行比较,如果某个元素比堆顶元素大,那我们就可以将堆顶元素进行剔除,转而将刚才那个元素入堆,操作就是互换两个元素位置,在将整棵树进行向下调整。反之,不在赘述。
分析思路二的时间复杂度:考虑最差的情况,如果是一个升序的情况,求前k个最大的值,那每次交换完堆顶的元素和后续某个元素之后,此时堆顶的元素需要向下调整至最底层,那k个元素的完全二叉树的深度是:log(k+1),从k+1个元素到第n个元素,总要与对顶元素互换位置,紧接着就是层层往下调整,直至调整至最底层,所以f(n)=(n-k)*log(k+1-1)即为要进行的向下调整的次数,每次都要进行交换,大不了就乘个2,由大O渐进发的性质可以知道,该方法的时间复杂度就是O(n);空间复杂度:因为是对一个定死的数组进行操作,不涉及额外的空间,所以空间复杂度就是O(1)
对思路2进行代码实现:
private static int[] topK(int[] array,int k){
if(array==null) return null;
if(k>array.length) return array;
//此处默认的就是小根堆,所以求出来的是前k个最大的值
PriorityQueue<Integer> priorityQueue=new PriorityQueue<>();
for(int i=0;i<k;i++){
priorityQueue.offer(array[i]);//假设前k个元素就是我们所求
}
for(int i=k+1;i<array.length;i++){
int front=priorityQueue.peek();
if(array[i]>front){
priorityQueue.poll();
priorityQueue.offer(array[i]);
}
}
int[] tmp=new int[k];
for(int i=0;i<k;i++){
tmp[i]=priorityQueue.poll();
}
return tmp;
}
public static void main(String[] args) {
int[] array={1,2,3,4,5,6,7,8,9,10};
int[] ret=topK(array,4);
System.out.println(Arrays.toString(ret));
}
Question:那我们想求前k个最小的元素,想建立大根堆怎么办?
此时的优先级队列为我们提供了一个带有两个参数的构造方法:
private static int[] topK(int[] array,int k){
if(array==null) return null;
if(k>array.length) return array;
PriorityQueue<Integer> priorityQueue=new PriorityQueue<>(k, new Comparator<Integer>() {
@Override
public int compare(Integer o1, Integer o2) {
return o2-o1;//别写反了
}
});
for(int i=0;i<array.length;i++){
if(priorityQueue.size()<k){
priorityQueue.offer(array[i]);
}else{
int front=priorityQueue.peek();
if(front>array[i]){
priorityQueue.poll();
priorityQueue.offer(array[i]);
}
}
}
int[] tmp=new int[k];
for(int i=0;i<k;i++){
tmp[i]=priorityQueue.poll();
}
return tmp;
}
public static void main(String[] args) {
int[] array={1,2,3,4,5,6,7,8,9,10};
int[] ret=topK(array,4);
System.out.println(Arrays.toString(ret));
}
讨论优先级队列
-
如果我们在优先级队列中放的元素不是此处的这些数字,那我们怎么才能实现堆顶“相对最小”的一个小根堆,或者反过来的大根堆呢?对此,我们需了解优先级队列的原码,是怎么处理的:
首先是无参构造:
public PriorityQueue() { this(DEFAULT_INITIAL_CAPACITY, null); } //private static final int DEFAULT_INITIAL_CAPACITY = 11; //后者的null其实是优先级队列的另一个字段:private final Comparator comparator;根据this的用法,我们可以知道,虽然我们使用时没给参数,但底层是调用了带有两个参数的构造方法的,过去看看:
public PriorityQueue(int initialCapacity, Comparator<? super E> comparator) { // Note: This restriction of at least one is not actually needed, // but continues for 1.5 compatibility if (initialCapacity < 1) throw new IllegalArgumentException(); this.queue = new Object[initialCapacity]; this.comparator = comparator; } //1:初始化了一个11个容量的数组 //2:比较器默认是null //3:顺带看一下,初始容量不能小于0那此时我们去向优先级队列中:放置一些我们自定义的类型时:
class Card{ public int rank; public String suit; public Card(int rank, String suit) { this.rank = rank; this.suit = suit; } } public class TestDemo{ public static void main(String[] args) { PriorityQueue<Card> priorityQueue=new PriorityQueue<>(); Card card1=new Card(3,"♥"); Card card2=new Card(2,"♠"); priorityQueue.offer(card1); priorityQueue.offer(card2); System.out.println("====="); } } //17行打断点,进行调试,会发现 Exception in thread "main" java.lang.ClassCastException: Card cannot be cast to java.lang.Comparable那为什么offer()时会抛出这个异常呢?去offer()原码看看:
public boolean offer(E e) { if (e == null) throw new NullPointerException(); modCount++; int i = size;//size在放置第一个元素的时候就是0 if (i >= queue.length) grow(i + 1);//length此时是11,i是0,所以不用扩容 size = i + 1;//数据还没放呢,先把size加1了 if (i == 0) queue[0] = e;//第一次放元素的时候,就直接放在第0号下标的地方,所以如果我们往优先级队列里就只放一个元素,那不会报错 else siftUp(i, e);//放第二个元素或者第三个...那都要进入shiftUp(i,e) return true; }所以我们放黑桃2的时候,涉及到shiftUp(),过去看看:
private void siftUp(int k, E x) {//放黑桃2的时候,此处k=1,x就是我们的黑桃2 if (comparator != null) siftUpUsingComparator(k, x); else siftUpComparable(k, x);//进入这个 }因为我们的比较器默认就是null,所以进入else:
private void siftUpComparable(int k, E x) { Comparable<? super E> key = (Comparable<? super E>) x; while (k > 0) { int parent = (k - 1) >>> 1;//根据儿子找双亲 Object e = queue[parent];//获取双亲对象 if (key.compareTo((E) e) >= 0)//孩子,也就是我们的e,也就是我们的黑桃2调用compareTo(),依据大小关系判断是否进入if语句 break; queue[k] = e; k = parent; } queue[k] = key; }综上可以看出,offer()第二个元素的时候,就会报错,即前述的第16行代码会最先出错,根据栈的特点,先进的后出,所以这个错误信息将最后打印出来。Debug结果也确实如此。
-
对于上述问题我们应当如何处理?
- 之前所学的对象的比较有两种:一种是对象的引用是否一致,在String一章中有大量提到,另外一种就是对象本身的某些内容的比较,那想解决上述问题,我们就必须给予Card对象之间能够进行比较的方法
- 对于上述方法,第一种是将Card类实现Comparable接口,并在Card类内重写compareTo函数;第二种就是专门为Card类写一个比较器,好让offer()在放第二个元素乃至后面的元素时有一个能使用的比较器
第一种:将Card类实现Comparable接口:(如只拿数字作比较)
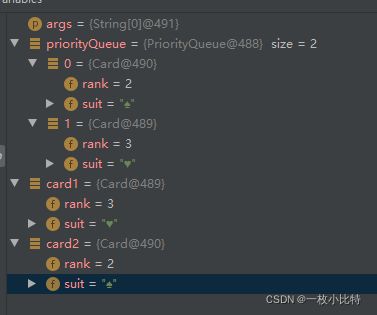
class Card implements Comparable<Card>{ public int rank; public String suit; public Card(int rank, String suit) { this.rank = rank; this.suit = suit; } @Override public int compareTo(Card o) { return this.rank-o.rank; } } public class TestDemo{ public static void main(String[] args) { PriorityQueue<Card> priorityQueue=new PriorityQueue<>(); Card card1=new Card(3,"♥"); Card card2=new Card(2,"♠"); priorityQueue.offer(card1); priorityQueue.offer(card2); System.out.println("====="); } }Debug结果:
第二张牌存放成功,并且是小根堆,如果将compareTo()中的返回值写成相反数,将建立大根堆!
第二种:专门为Card类写一个比较器
class Card{ public int rank; public String suit; public Card(int rank, String suit) { this.rank = rank; this.suit = suit; } } class RankComparator implements Comparator<Card>{ @Override public int compare(Card o1,Card o2){ return o1.rank-o2.rank; } } public class TestDemo{ public static void main(String[] args) { RankComparator rankComparator=new RankComparator(); PriorityQueue<Card> priorityQueue=new PriorityQueue<>(rankComparator); Card card1=new Card(3,"♥"); Card card2=new Card(2,"♠"); priorityQueue.offer(card1); priorityQueue.offer(card2); System.out.println("====="); } }
上述两种方法的区别
第一种对Card类侵入性太强,而第二种对Card类没有变动。
对于第二种,我们可以有特殊写法,就不用专门去写一个比较器了,代码如下:
1:(匿名内部类)
class Card{ public int rank; public String suit; public Card(int rank, String suit) { this.rank = rank; this.suit = suit; } } public class TestDemo{ public static void main(String[] args) { PriorityQueue<Card> priorityQueue=new PriorityQueue<>(new Comparator<Card>() { @Override public int compare(Card o1, Card o2) { return o2.rank-o1.rank;//这里将使得构建的堆变成大根堆 } }); Card card1=new Card(3,"♥"); Card card2=new Card(2,"♠"); priorityQueue.offer(card1); priorityQueue.offer(card2); System.out.println("====="); } }2:lambda表达式(可读性较差)
class Card{ public int rank; public String suit; public Card(int rank, String suit) { this.rank = rank; this.suit = suit; } } public class TestDemo{ public static void main(String[] args) { PriorityQueue<Card> priorityQueue=new PriorityQueue<>((x,y)->{return x.rank-y.rank;}); Card card1=new Card(3,"♥"); Card card2=new Card(2,"♠"); priorityQueue.offer(card1); priorityQueue.offer(card2); System.out.println("====="); } }