2022年第十三届蓝桥杯C/C++ B组第一场省赛题解
2022年第十三届C/C++ B组第一场蓝桥杯省赛题解
- A:九进制转十进制
- B:顺子日期
- C:刷题统计
- D:修剪灌木
- E:X 进制减法
- F:统计子矩阵
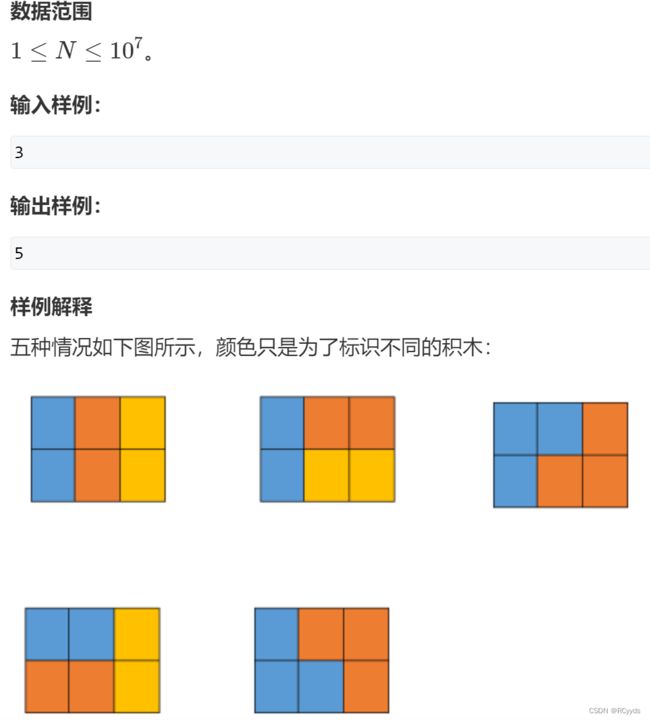
- G:积木画
- H:扫雷
- I:李白打酒加强版
- J:砍竹子
A:九进制转十进制

答案:1478
解析:很简单的进制转换题,2✖(9✖9✖9+9+1)=1478。
B:顺子日期

答案:14
解析:这道题有争议,网上有三种答案,分别是4,14,5,我的答案是14。我的解法就完全是按照做题直觉来的,顺子应该是升序的,且012也算。
以下为具体解法:
2022mmdd,有两种大情况,前面三位mmd是顺子和后面三位mdd是顺子。首先是mmd是顺子,mmd可以为012,那么有10种情况,mmd可以为123,有2种情况;最后是mdd是顺子,mdd可以为012,1种情况,可以为123,2种情况。前面算的加起来为15种情况,再减去算重的情况也就是前面三个和后面三个都是顺子的情况0123,所以最终答案为14。
C:刷题统计
#include
using namespace std;
typedef long long ll;
ll a,b,n,ans=0;
int main()
{
cin>>a>>b>>n;
ans=n/(5*a+2*b)*7;
ll t=n-ans/7*(5*a+2*b);
int day=1;
while(t>0)
{
if(day!=6&&day!=7) t-=a;
else t-=b;
ans++;
day++;
}
cout< 解析:首先这道题数据范围很大,有10的18次方,故不能暴力枚举天数来做。我们可以先算一周能做多少题,看刷完n题要几周完成,没满整周的题数算出来,根据这个算出还要做几天才做完n题,加起来就是答案了。
D:修剪灌木
#include
using namespace std;
int main()
{
int n;
cin>>n;
for(int i=1;i<=n;i++)
{
int a=i;
int b=2*(i-1);
int c=2*(n-i);
int ans=max(max(a,b),c);
cout< 解析:这道题就是模拟找规律,有三种情况,分别是第一、二、三次走到目标位置灌木长的高度,在这三种情况中取最大值。
E:X 进制减法
#include
using namespace std;
const int M=1e5+5,mod=1e9+7;
typedef long long LL;
int a[M], b[M], w[M];
int n;
int Ma, Mb;
LL mul[M];
int A, B;
int main()
{
int n,Ma,Mb;
cin>>n;
cin>>Ma;
for(int i=Ma;i>=1;i--) cin>>a[i];
cin>>Mb;
for(int i=Mb;i>=1;i--) cin>>b[i];
int M=max(Ma,Mb);
for(int i=M;i>=1;i--)
{
int t=max(a[i],b[i]);
w[i]=max(2,t+1);
}
mul[1]=1;
for(int i=2;i<=M;i++)
{
mul[i]=mul[i-1]*w[i-1]%mod;
}
for(int i=Ma;i>=1;i--)
A=(A+a[i]*mul[i])%mod;
for(int i=Mb;i>=1;i--)
B=(B+b[i]*mul[i])%mod;
cout<<(A-B+mod)%mod;
return 0;
}
解析:这道题用贪心就可以很简单的解决这道题。数的每位都选用对A和B来说合理的进制最小但不低于2的进制,A-B的值最小。就比如第i位,A的数为3,B的数为4,对A来说进制最小为4,对B来说进制最小为5,那么对A和B来说该位合理的进制最小为5。每位的进制得出来后,再算出每位的权值。在这里要注意在算权值时是会爆int的,两个int值相乘会爆int,即使取模,在取模前就爆了,所以权值要用long long来存,但算A和B时,是不会爆int的,因为会分别取模,两个在1e9+7范围内的数相加是不会爆int的,这个要注意!如果你不想那么麻烦,也可以全都用long long来存,答案不会变,就是耗时长一点。
F:统计子矩阵
code:
#include
using namespace std;
const int N=5e2+10;
int a[N][N];
int main()
{
int n,m,k;
long long ans=0;
scanf("%d%d%d",&n,&m,&k);
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
scanf("%d",&a[i][j]);
a[i][j]+=a[i-1][j]+a[i][j-1]-a[i-1][j-1];
}
}
for(int i=1;i<=m;i++)
{
for(int j=i;j<=m;j++)
{
for(int s=1,t=1;t<=n;t++)
{
while(s<=t&&a[t][j]-a[t][i-1]-a[s-1][j]+a[s-1][i-1]>k) s++;
if(s<=t) ans+=t-s+1;
}
}
}
printf("%lld",ans);
return 0;
}
解析:这道题要用前缀和双指针的知识。
以下为示意图:
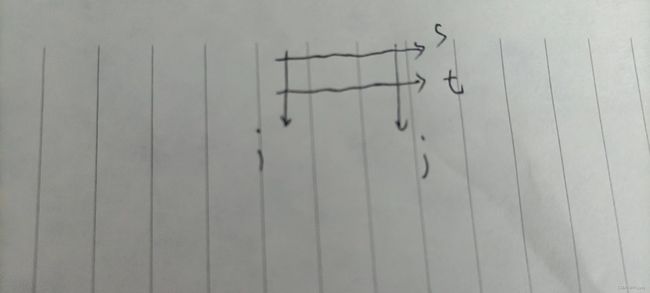
s和t是能动的指针,i和j固定。我们在做的时候遍历i和j,然后在循环内遍历t,s往下动的条件是s<=t&&a[t][j]-a[t][i-1]-a[s-1][j]+a[s-1][i-1]>k,这里要用while循环,直道s>t或里面的数之和小于或等于k,如果是小于或等于k的情况就是我们想要的答案了,ans+=t-s+1,为什么是加t-s+1呢?因为s往下都是符合条件的答案。接着t++,再一次循环遍历上述流程。
G:积木画
#include
using namespace std;
const int mod=1e9+7;
long long f[2][3];
int main()
{
int n;
scanf("%d",&n);
f[1][0]=1;
f[1][1]=2;
f[1][2]=1;
for(int i=2;i<=n;i++)
{
f[i&1][0]=(f[i-1&1][0]+f[i-1&1][2])%mod;
f[i&1][1]=(f[i-1&1][0]*2+f[i-1&1][1])%mod;
f[i&1][2]=(f[i-1&1][0]+f[i-1&1][1])%mod;
}
printf("%lld",f[n&1][0]);
return 0;
}
解析:这道题咋一看是不是有点像蒙德里安的梦想这道状压DP题,但其实比那道题简单多了,因为这里规定了长度为2,那么表示状态就好表示多了,用线性DP就可以解决。
规定f[i][j]:前i列已填满,第i+1列填了j个方块,那么答案就是f[n][0]。在这里要注意n的取值最大可为10的7次方,数组空间会超的,但我们都是相邻两列进行比较,所以我们可以用滚动数组来做。
H:扫雷
code:
#include
using namespace std;
const int N=5e4+10,M=1e6+7,X=1e9+1;
struct node{
int x,y,r;
}b[N];
typedef long long ll;
ll h[M];// 哈希数组
int id[M],res;// id数组为哈希数组中key对应的地雷下标
bool st[N];// 判断是否访问过
ll get_hs(int x,int y)// 得到每个坐标的哈希值
{
return (ll)x*X+y;
}
int find(int x,int y)
{
ll hs=get_hs(x,y);// 找到该坐标被哈希数组存储的下标key
int key=(hs%M+M)%M;// 映射到哈希数组内部
// 如果该位置已经被占用并且不等于我们要求的哈希值,要在之后找到相应位置
while(h[key]!=-1&&h[key]!=hs)
{
key++;
if(key==M) key=0;// 哈希表走到末尾,又从0开始
}
return key;
}
// 判断x1,y1为圆心,半径为r的圆是否包含x,y
bool check(int x1,int y1,int r,int x,int y)
{
int d=(x1-x)*(x1-x)+(y1-y)*(y1-y);
return d<=r*r;
}
void bfs(int pos)
{
queue q;
q.push(pos);
st[pos]=1;
while(!q.empty())
{
int t=q.front();
q.pop();
int x=b[t].x,y=b[t].y,r=b[t].r;
for(int xx=x-r;xx<=x+r;xx++)
{
for(int yy=y-r;yy<=y+r;yy++)
{
int key=find(xx,yy);// 找到该坐标点对应的哈希下标
// 该点是不是地雷,有没有被访问过,能不能炸到
if(id[key]&&!st[id[key]]&&check(x,y,r,xx,yy))
{
int pos=id[key];// 获得对应地雷编号
st[pos]=1;
q.push(pos);
}
}
}
}
}
int main()
{
int n,m;
cin>>n>>m;
memset(h,-1,sizeof(h));
int x,y,r;
for(int i=1;i<=n;i++)// 读入地雷,存入哈希表
{
cin>>x>>y>>r;
b[i].x=x,b[i].y=y,b[i].r=r;
int key=find(x,y);// 找到该坐标点对应的哈希下标
if(h[key]==-1) h[key]=get_hs(x,y);// 如果哈希对应位置为空,则插入
// id数组没有被标记或者找到了同一个坐标点更大半径的地雷
if(!id[key]||b[id[key]].r>x>>y>>r;
for(int xx=x-r;xx<=x+r;xx++)
{
for(int yy=y-r;yy<=y+r;yy++)
{
int key=find(xx,yy);
// 如果该点有地雷,没有被访问过,能被炸到
if(id[key]&&!st[id[key]]&&check(x,y,r,xx,yy)) bfs(id[key]);
}
}
}
// 遍历每个地雷,看是否被标记
for(int i=1;i<=n;i++)
{
int key=find(b[i].x,b[i].y);// 获得坐标点对应哈希下标
int pos=id[key];// 哈希下标对应的地雷编号
if(pos&&st[id[key]]) res++;// 如果有地雷并且被访问过
}
cout< 解析:这道题挺麻烦的,本来用bfs加unordered_map
1.M为哈希表的长度,哈希表的长度至少是2n,不过在实际中应该尽可能的大点,且最好为质数,这里就用了1e6+7。
2.X的作用就是让坐标x和y合起来,映射为一个数,且每个数是不同的,因为这里x,y范围为1e9,所以X就选了1e9+1。
I:李白打酒加强版
1.标答code:
#include
using namespace std;
const int N=105,mod=1e9+7;
int f[N][N][N];
int n,m;
int main()
{
cin>>m>>n;
f[0][0][2]=1;
for(int i=0;i<=n;i++)
{
for(int j=0;j<=m;j++)
{
for(int k=0;k0)
{
f[i][j][k]=(f[i][j][k]+f[i-1][j][k+1])%mod;
}
if(j>0&&k%2==0)
{
f[i][j][k]=(f[i][j][k]+f[i][j-1][k/2])%mod;
}
}
}
}
cout< 2.我的dfs code:
#include
using namespace std;
int n,m;
long long num;
int mod=1e9+7;
int ans=0;
string s="";
void dfs(int k)
{
if(k>n+m)
{
num=2;
//cout<0)
num=num-1;
else break;
}
if(s[i]=='1') {
b++;
num=num*2;
}
}
if((num==0)&&(i==n+m)&&a==m&&b==n){
ans++;
ans=ans%mod;
}
return;
}
s+='0';
dfs(k+1);
if(s.length()!=1)
s=s.substr(0,k-1);
else s="";
s+='1';
dfs(k+1);
}
int main()
{
cin>>n>>m;
dfs(1);
cout< 解析:这道题也是用线性DP来解决,有些人可能用了dfs来写,就比如我。。。dfs只能过部分例子,正确解法是线性DP。
我们规定f[i][j][k]:经过i个花和j个店时酒还有k斗,那么答案就是f[i-1][j][1],为啥不是f[i][j][0]呢?因为题目里说了最后一次遇到的是花,f[i][j][0]包含了最后一次遇到店的情况。
J:砍竹子
#include
using namespace std;
typedef long long ll;
const int N=2e5+10;
ll a[N];
vector b[N];
int n;
ll change(ll x)
{
return sqrt(x/2+1);
}
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++) scanf("%lld",&a[i]);
int res=0;
for(int i=1;i<=n;i++)
{
while(a[i]>1)
{
int flag=0;
for(ll j:b[i-1])
{
if(a[i]==j)
{
flag=1;
break;
}
}
if(!flag) res++;
b[i].push_back(a[i]);
a[i]=change(a[i]);
}
}
printf("%d",res);
return 0;
}
解析:这道题据说有人用set来写,也有人用线段树来写等等,但其实有非常简单的近乎O(n)的暴力做法,就是我们这个做法了。我们用a[]数组存一开始每个竹子的高度,vector b[]存每个竹子使用魔法后的高度,我们每次拿当前使用魔法后的竹子高度与上一个竹子使用魔法后的全部高度进行比较,没有相同的就加一,反之不加,这样就能解决这道题了。