数据结构之数组和广义表
文章目录
- 第5章 数组和广义表
-
- 5.1 数组的定义
- 5.2 数组的顺序表示和实现
- 5.3 矩阵的压缩存储
-
- 5.3.1 特殊矩阵
- 5.3.2 稀疏矩阵
- 5.4 广义表
-
- 5.4.1 广义表的存储结构
第5章 数组和广义表
科学计算中涉及到大量的矩阵问题,在程序设计语言中一般都采用数组来存储,被描述成一个二维数组。但当矩阵规模很大且具有特殊结构(对角矩阵、三角矩阵、对称矩阵、稀疏矩阵等),为减少程序的时间和空间需求,采用自定义的描述方式。
5.1 数组的定义
数组是由 n ( n > 1 ) n(n>1) n(n>1)个具有相同数据类型的数据元素 a 1 , a 2 , … , a n a_1,a_2,…,a_n a1,a2,…,an组成的有序序列,且该序列必须存储在一块地址连续的存储单元中。
5.2 数组的顺序表示和实现
数组一般不做插入和删除操作,也就是说,数组一旦建立,结构中的元素个数和元素间的关系就不再发生变化。因此,一般都是采用顺序存储的方法来表示数组。
问题:计算机的内存结构是一维(线性)地址结构,对于多维数组,将其存放(映射)到内存一维结构时,有个次序约定问题。
二维数组是最简单的多维数组,以此为例说明多维数组存放(映射)到内存一维结构时的次序约定问题。
通常有两种顺序存储方式
- 行优先顺序(Row Major Order) :将数组元素按行排列,第 i + 1 i+1 i+1 个行向量紧接在第 i i i 个行向量后面。对二维数组,按行优先顺序存储的线性序列为:
a 11 , a 12 , … , a 1 n , a 21 , a 22 , … a 2 n , … … , a m 1 , a m 2 , … , a m n a11,a12,…,a1n, a21,a22,…a2n ,……, am1,am2,…,amn a11,a12,…,a1n,a21,a22,…a2n,……,am1,am2,…,amn
- 列优先顺序(Column Major Order) :将数组元素按列向量排列,第 j + 1 j+1 j+1 个列向量紧接在第 j j j 个列向量之后,对二维数组,按列优先顺序存储的线性序列为:
a 11 , a 21 , … , a m 1 , a 12 , a 22 , … a m 2 , … … , a n 1 , a n 2 , … , a n m a11,a21,…,am1, a12,a22,…am2, ……, an1,an2,…,anm a11,a21,…,am1,a12,a22,…am2,……,an1,an2,…,anm
设有二维数组 A = ( a i j ) m × n A=(a_{ij})_{m\times n} A=(aij)m×n,若每个元素占用的存储单元数为 l l l (个), L O C [ a 11 ] LOC[a_{11}] LOC[a11]表示元素 a 11 a_{11} a11 的首地址,即数组的首地址。
- 以“行优先顺序”存储存储
(1) 第1行中的每个元素对应的(首)地址是:
L O C [ a 1 j ] = L O C [ a 11 ] + ( j − 1 ) × l j = 1 , 2 , … , n LOC[a_{1j}]=LOC[a_{11}]+(j-1)\times l \quad j=1,2, …,n LOC[a1j]=LOC[a11]+(j−1)×lj=1,2,…,n
(2) 第2行中的每个元素对应的(首)地址是:
L O C [ a 2 j ] = L O C [ a 11 ] + n × l + ( j − 1 ) × l j = 1 , 2 , … , n LOC[a_{2j}]=LOC[a_{11}]+n\times l+(j-1)\times l \quad j=1,2, …,n LOC[a2j]=LOC[a11]+n×l+(j−1)×lj=1,2,…,n
(3) 第m行中的每个元素对应的(首)地址是:
L O C [ a m j ] = L O C [ a 11 ] + ( m − 1 ) × n × l + ( j − 1 ) × l j = 1 , 2 , … , n LOC[a_{mj}]=LOC[a_{11}]+(m-1)\times n\times l+(j-1)\times l \quad j=1,2, …,n LOC[amj]=LOC[a11]+(m−1)×n×l+(j−1)×lj=1,2,…,n
由此可知,二维数组中任一元素aij的(首)地址是:
L O C [ a i j ] = L O C [ a 11 ] + [ ( j − 1 ) × m + ( i − 1 ) ] × l i = 1 , 2 , … , n j = 1 , 2 , … , m LOC[a_{ij}]=LOC[a_{11}]+[(j-1) \times m+(i-1)] \times l \\ \text{}\\ i=1,2, …,n \quad j=1,2, …,m LOC[aij]=LOC[a11]+[(j−1)×m+(i−1)]×li=1,2,…,nj=1,2,…,m
对于三维数组 A = ( a i j k ) m × n × p A=(a_{ijk})_{m\times n\times p} A=(aijk)m×n×p,若每个元素占用的存储单元数为l(个),三维数组中任一元素 a i j k a_{ijk} aijk的(首)地址是:
L O C ( a i j k ) = L O C [ a 111 ] + [ ( i − 1 ) × n × p + ( j − 1 ) × p + ( k − 1 ) ] × l LOC(a_{ijk})=LOC[a_{111}]+[(i-1)\times n\times p+(j-1)\times p+(k-1)]\times l LOC(aijk)=LOC[a111]+[(i−1)×n×p+(j−1)×p+(k−1)]×l
n维数组中任一元素 a j 1 j 2 … j n a_{j_1j_2…j_n} aj1j2…jn的(首)地址是:
LOC [ a j 1 j 2 … j n ] = LOC [ a 11 … 1 ] + [ ( b 2 × ⋯ × b n ) × ( j 1 − 1 ) + [ ( b 3 × ⋯ × b n ) × ( j 2 − 1 ) + … + b n × ( j n − 1 − 1 ) + j n − 1 ] × l \begin{aligned} \operatorname{ LOC}[a_{j_1j_2\dots j_n }]&=\operatorname{ LOC}[a_{11\dots1}]\\ &+[(b2\times\dots\times b_n)\times(j_1-1)\\ &+[(b3\times\dots\times b_n)\times(j_2-1)+\dots\\ &+b_n\times (j_{n-1}-1)+j_n-1]\times l \end{aligned} LOC[aj1j2…jn]=LOC[a11…1]+[(b2×⋯×bn)×(j1−1)+[(b3×⋯×bn)×(j2−1)+…+bn×(jn−1−1)+jn−1]×l
- 以“列优先顺序”存储
略
5.3 矩阵的压缩存储
5.3.1 特殊矩阵
- 对称矩阵
若一个 n n n 阶方阵 A = ( a i j ) n × n A=(a_{ij})_{n\times n} A=(aij)n×n 中的元素满足性质:
a i j = a j i 1 ≤ i , j ≤ n and i ≠ j a_{ij}=a_{ji} \quad 1\le i,j\le n \quad \operatorname{and} \quad i \ne j aij=aji1≤i,j≤nandi=j
则称 A A A为对称矩阵。
对称矩阵中的元素关于主对角线对称,因此,让每一对对称元素 a i j a_{ij} aij 和 a j i ( i ≠ j ) a_{ji}(i≠j) aji(i=j) 分配一个存储空间,则 n 2 n^2 n2 个元素压缩存储到 n ( n + 1 ) / 2 n(n+1)/2 n(n+1)/2 个存储空间,能节约近一半的存储空间。
不失一般性,假设按“行优先顺序”存储下三角形(包括对角线)中的元素。
设用一维数组(向量) s a [ 0 … n ( n + 1 ) / 2 − 1 ] sa[0…n(n+1)/2-1] sa[0…n(n+1)/2−1] 存储 n n n 阶对称矩阵,如图5-4所示。为了便于访问,必须找出矩阵A中的元素的下标值 ( i , j ) (i,j) (i,j)和向量sa[k]的下标值k之间的对应关系。
对称矩阵元素 a i j a_{ij} aij 保存在向量sa中的下标值 k k k 与 ( i , j ) (i,j) (i,j)之间的对应关系是:
k = { i × ( i − 1 ) / 2 + j − 1 当 i ≥ j 时 j × ( j − 1 ) / 2 + i − 1 当 i < j 时 1 ≤ i , j ≤ n k=\left\{\begin{array}{ll} i \times(i-1) / 2+j-1 & \text { 当 } i \ge j \text { 时 } \\ j \times(j-1) / 2+i-1 & \text { 当 } i
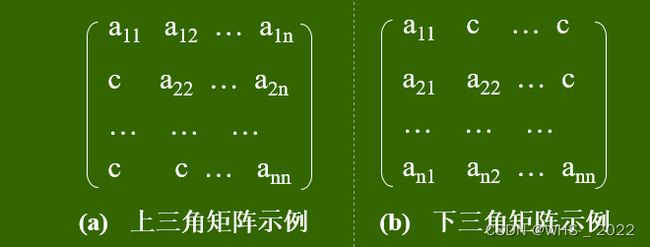
2. 三角矩阵
以主对角线划分,三角矩阵有上三角和下三角两种。
上三角矩阵的下三角(不包括主对角线)中的元素均为常数c(一般为0)。下三角矩阵正好相反,它的主对角线上方均为常数
三角矩阵中的重复元素 c c c 可共享一个存储空间,其余的元素正好有 n ( n + 1 ) / 2 n(n+1)/2 n(n+1)/2个,因此,三角矩阵可压缩存储到向量sa[0…n(n+1)/2]中,其中 c c c存放在向量的第1个或最后1个分量中。
3.对角矩阵
矩阵中,除了主对角线和主对角线上或下方若干条对角线上的元素之外,其余元素皆为零。即所有的非零元素集中在以主对角线为了中心的带状区域中,如图5-6所示。
如上图三对角矩阵,非零元素仅出现在主对角( a i , i , 1 ≤ i ≤ n a_{i, i},1\le i\le n ai,i,1≤i≤n)上、主对角线上的那条对角线( a i , i + 1 , 1 ≤ i ≤ n − 1 a_{i, i+1},1\le i\le n-1 ai,i+1,1≤i≤n−1) 、主对角线下的那条对角线上( a i + 1 , i , 1 ≤ i ≤ n − 1 a_{i+1, i},1\le i\le n-1 ai+1,i,1≤i≤n−1)。显然,当 ∣ i − j ∣ > 1 |i-j |>1 ∣i−j∣>1 时,元素 a i j = 0 a_{ij}=0 aij=0
对角矩阵可按行优先顺序或对角线顺序,将其压缩存储到一个向量中,并且也能找到每个非零元素和向量下标的对应关系。
对这种矩阵,当以按“行优先顺序”存储时, 第 1 1 1 行和第 n n n 行是 2 2 2 个非零元素,其余每行的非零元素都要是 3 3 3 个,则需存储的元素个数为 3 n − 2 3n-2 3n−2。
5.3.2 稀疏矩阵
稀疏矩阵(Sparse Matrix):对于稀疏矩阵,目前还没有一个确切的定义。设矩阵A是一个 m × n m\times n m×n的矩阵中有s个非零元素,设 δ = s / ( m × n ) δ=s/(m\times n) δ=s/(m×n),称 δ δ δ为稀疏因子,如果某一矩阵的稀疏因子 δ δ δ满足 δ ≤ 0.05 δ\le 0.05 δ≤0.05时称为稀疏矩阵,如图5-8所示。
A = ( 0 12 9 0 0 0 0 0 0 0 0 0 0 0 0 0 − 3 0 0 0 0 0 0 4 0 0 24 0 0 2 0 0 0 18 0 0 0 0 0 0 0 0 0 0 0 0 − 7 0 0 0 0 − 6 0 0 0 0 ) A=\left(\begin{array}{cccccccc} 0 & 12 & 9 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ -3 & 0 & 0 & 0 & 0 & 0 & 0 & 4 \\ 0 & 0 & 24 & 0 & 0 & 2 & 0 & 0 \\ 0 & 18 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & -7 & 0 \\ 0 & 0 & 0 & -6 & 0 & 0 & 0 & 0 \end{array}\right) A= 00−3000012000180090024000000000−60000000000200000000−700040000
typedef struct
{
int rn; /* 行数 */
int cn; /* 列数 */
int tn; /* 非0元素个数 */
Triple data[MAX_SIZE];
} TMatrix;
求转置矩阵的基本算法思想是:
方法一:
算法思想:按稀疏矩阵A的三元组表a.data中的列次序依次找到相应的三元组存入b.data中。
① 将矩阵的行、列下标值交换。即将三元组表中的行、列位置值i 、j相互交换;
② 重排三元组表中元素的顺序。即交换后仍然是按行优先顺序排序的。
void TransMatrix(TMatrix a, TMatrix &b)
{
int p, q, col;
b.rn = a.cn;
b.cn = a.rn;
b.tn = a.tn;
/* 置三元组表b.data的行、列数和非0元素个数 */
if (b.tn == 0)
printf(“ The Matrix A = 0\n”);
else
/* 仔细结合P98图 */
{
q = 1;
for (col = 1; col <= a.cn; col++)
/* 每循环一次找到转置后行号为col的若干三元组 */
for (p = 1; p <= a.tn; p++)
/* 循环次数是第col行中非0元素个数 */
if (a.data[p].col == col)
{
b.data[q].row = a.data[p].col;
b.data[q].col = a.data[p].row;
b.data[q].value = a.data[p].value;
q++; /*表示下次要交换的三元组*/
}
}
}
当非零元素的个数tn和 m × n m\times n m×n同数量级时,算法TransMatrix的时间复杂度为 O ( m × n 2 ) O(m\times n^2) O(m×n2)。
而一般传统矩阵的转置算法为:
for (col = 1; col <= n; ++col)
for (row = 0; row <= m; ++row)
b[col][row] = a[row][col];
其时间复杂度为 O ( m × n ) O(m\times n) O(m×n)。
方法二:
(快速转置的算法)
col 1 2 3 4 5 6 7 8 num [ col ] 1 2 2 1 0 1 1 1 cpot [ c o l ] 1 2 4 6 7 7 8 9 \begin{array}{|c|c|c|c|c|c|c|c|c|} \hline \text { col } & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 \\ \hline \text { num }[\text { col }] & 1 & 2 & 2 & 1 & 0 & 1 & 1 & 1 \\ \hline \text { cpot }[\mathrm{col}] & 1 & 2 & 4 & 6 & 7 & 7 & 8 & 9 \\ \hline \end{array} col num [ col ] cpot [col]111222324416507617718819
显然有位置对应关系:
{ cpot [ 1 ] = 1 cpot [ col ] = cpot [ col − 1 ] + num [ col − 1 ] 2 ≤ col ≤ a ⋅ c n \left\{\begin{array}{l} \operatorname{cpot}[1]=1 \\ \operatorname{cpot}[\operatorname{col}]=\operatorname{cpot}[\operatorname{col}-1]+\text { num }[\operatorname{col}-1] \quad 2 \leq \operatorname{col} \leq a \cdot c n \end{array}\right. {cpot[1]=1cpot[col]=cpot[col−1]+ num [col−1]2≤col≤a⋅cn
void FastTransMatrix(TMatrix a, TMatrix &b)
{
int p, q, col, k;
int num[MAX_SIZE], copt[MAX_SIZE];
/* 置三元组表b.data的行、列数和非0元素个数 */
b.rn = a.cn;
b.cn = a.rn;
b.tn = a.tn;
if (b.tn == 0)
printf(“The Matrix A = 0\n”);
else
{
for (col = 1; col <= a.cn; ++col)
num[col] = 0;
/* 向量num[]初始化为0 */
for (k = 1; k <= a.tn; ++k)
++num[a.data[k].col] /* 求原矩阵中每一列非0元素个数 结合课本98-99表*/
for (cpot[1] = 1, col = 2; col <= a.cn; ++col)
cpot[col] = cpot[col - 1] + num[col - 1];
/* 求第col列中第一个非0元在b.data中的序号 */
for (p = 1; p <= a.tn; ++p) /*处理a的第p个元素*/
{
col = a.data[p].col;
q = cpot[col];
b.data[q].row = a.data[p].col;
b.data[q].col = a.data[p].row;
b.data[q].value = a.data[p].value;
++cpot[col]; /*至关重要!!当本列中有多个元素,下一元素位置加一*/
}
}
}
5.4 广义表
在第2章中,我们把线性表定义为 n ( n ≥ 0 ) n(n\ge 0 ) n(n≥0)个元素 a 1 , a 2 , … , a n a1, a2 ,…, an a1,a2,…,an的有穷序列,该序列中的所有元素具有相同的数据类型且只能是原子项(Atom)。所谓原子项可以是一个数或一个结构,是指结构上不可再分的。若放松对元素的这种限制,容许它们具有其自身结构,就产生了广义表的概念。
广义表(Lists,又称为列表 ):是由 n ( n ≥ 0 ) n(n \ge 0) n(n≥0)个元素组成的有穷序列: L S = ( a 1 , a 2 , … , a n ) LS=(a1,a2,…,an) LS=(a1,a2,…,an)
习惯上:原子用小写字母,子表用大写字母。
若广义表LS非空时:
-
其余元素组成的子表称为表尾;(a2,a3,…,an)
-
广义表中所包含的元素(包括原子和子表)的个数称为表的长度。
-
广义表中括号的最大层数称为表深 (度)。
-
广义表中括号第一层的元素个数称为表长
-
a 1 a1 a1 (表中第一个元素)称为表头;
根据对表头、表尾的定义,任何一个非空广义表的表头可以是原子,也可以是子表, 而表尾必定是广义表。
广义 表 表长n 表深h A = ( ) 0 1 B = ( e ) 1 1 C = ( a , ( b , c , d ) ) 2 2 D = ( A , B , C ) 3 3 E = ( a , E ) 2 ∞ F = ( ( ) ) 1 2 \begin{array}{|l|c|c|} \hline \text { 广义 表 } & \text { 表长n } & \text { 表深h } \\ \hline \mathbf{A}=() & 0 & 1 \\ \hline \mathbf{B}=(e) & 1 & 1 \\ \hline \mathbf{C}=(a,(b, c, d)) & 2 & 2 \\ \hline \mathbf{D}=(\mathbf{A}, \mathbf{B}, \mathbf{C}) & 3 & 3 \\ \hline \mathbf{E}=(a, \mathbf{E}) & 2 & \infty \\ \hline \mathbf{F}=(()) & 1 & 2\\ \hline \end{array} 广义 表 A=()B=(e)C=(a,(b,c,d))D=(A,B,C)E=(a,E)F=(()) 表长n 012321 表深h 1123∞2
5.4.1 广义表的存储结构
由于广义表中的数据元素具有不同的结构,通常用链式存储结构表示,每个数据元素用一个结点表示。因此,广义表中就有两类结点:
◆ 一类是表结点,用来表示广义表项,由标志域,表头指针域,表尾指针域组成;
◆ 另一类是原子结点,用来表示原子项,由标志域,原子的值域组成。如图5-13所示。
只要广义表非空,都是由表头和表尾组成。即一个确定的表头和表尾就唯一确定一个广义表。
typedef struct GLNode
{
int tag; /* 标志域,为1:表结点;为0 :原子结点 */
union
{
elemtype value; /* 原子结点的值域 */
struct
{
struct GLNode *hp, *tp;
} ptr; /* ptr和atom两成员共用 */
};
} *GList; /* 广义表类型 */
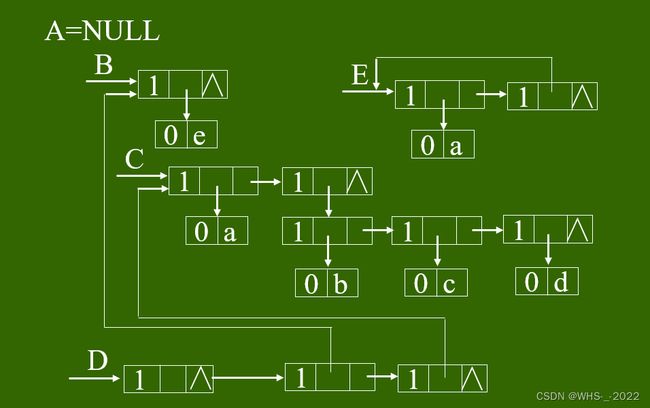
例: 对 A = ( ) A=() A=(), B = ( e ) B=(e) B=(e), C = ( a , ( b , c , d ) ) C=(a, (b, c, d) ) C=(a,(b,c,d)), D = ( A , B , C ) D=(A, B, C) D=(A,B,C), E = ( a , E ) E=(a, E) E=(a,E)的广义表的存储结构如图5-14所示。