深入理解生成对抗网络（GAN 基本原理，训练崩溃，训练技巧，DCGAN，CGAN，pix2pix，CycleGAN）

生成对抗网络（generative adversarial networks，GAN）是一种基于博弈的生成模型，在图像生成等领域被广泛使用。GAN 由生成网络和判别网络组成，生成网络自动生成数据，判别网络判断数据是真还是假（由生成网络生成）。学习的目标是构建生成网络，能自动生成同已给训练数据同分布的数据。学习的过程就是博弈的过程，生成网络和判别网络不断通过优化自己网络的参数进行博弈。当达到均衡状态（纳什均衡）时，学习结束，生成网络可以生成以假乱真的数据，判别网络难以判断数据的真假。

GAN 基本模型

模型

如果想从已给训练数据中学习生成数据的模型，用模型自动生成新的数据，包括图像、语音数据，那么一个直接的方法是假设已给数据是由一个概率分布产生的数据，通过极大似然估计学习这个概率分布。但当数据分布非常复杂时，很难给出适当的概率密度函数的定义，以及有效地学习概率密度函数。GAN 不直接定义和学习数据生成的概率分布，而是通过导入评价生成数据“真假”的机制来解决这个问题。

GAN 的训练数据并没有直接用于生成网络的学习，而是用于判别网络的学习。判别网络能力提高之后用于生成网络能力的提高，生成网络能力提高之后再用于判别网络能力的提高，不断循环。

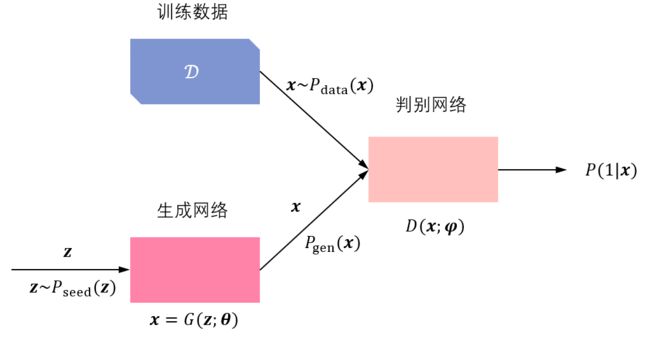
下图显示 GAN 的框架。假设已给训练数据 $\mathcal{D}$ 遵循分布 $P_{\text{data}}(\mathbf{x})$，其中 $\mathbf{x}$ 是样本。生成网络用 $\mathbf{x}=G(\mathbf{z};\mathbf{\theta })$ 表示，其中 $\mathbf{z}$ 是输入向量，$\mathbf{x}$ 是输出向量（生成数据），$\mathbf{\theta }$ 是网络参数。判别网络是一个二分类器，用 $P(1|\mathbf{x})=D(\mathbf{x};\mathbf{\phi })$ 表示，其中 $P(1|\mathbf{x})$ 和 $1-P(1|\mathbf{x})$ 是输出概率，分布表示输入 $\mathbf{x}$ 来自训练数据和生成数据的概率，$\mathbf{\phi }$ 是网络参数。输入向量（种子）遵循分布 $P_{\text{seed}}(\mathbf{z})$，如标准正态分布或均匀分布。生成网络生成的数据分布表示为 $P_{\text{gen}}(\mathbf{x})$，由 $P_{\text{seed}}(\mathbf{z})$ 和 $\mathbf{x}=G(\mathbf{z};\mathbf{\theta })$ 决定。

如果生成网络参数 $\mathbf{\theta }$ 固定，可以通过最大化以下目标函数学习判别网络参数 $\mathbf{\phi }$，使其具有判别真假数据的能力。
$$\underset{\mathbf{\phi }}{\max }\{E_{\mathbf{x}\sim P_{\text{data}}(\mathbf{x})}[\log D(\mathbf{x};\mathbf{\phi })]+E_{\mathbf{z}\sim P_{\text{seed}}(\mathbf{z})}[\log (1-D(G(\mathbf{z};\mathbf{\theta });\bar{\mathbf{\phi }}))]\}$$ $E_{\mathbf{x}\sim P_{\text{data}}(\mathbf{x})}[\log D(\mathbf{x};\mathbf{\phi })]$ 表示，对于从真实数据分布中采样的样本，其被判别器判定为真实样本概率的对数的数学期望。预测为正样本的概率越接近 1 越好，即这一项越大越好；

$E_{\mathbf{z}\sim P_{\text{seed}}(\mathbf{z})}[\log (1-D(G(\mathbf{z};\mathbf{\theta });\bar{\mathbf{\phi }}))]$ 则表示将生成网络生成的图片输入判别网络，这一项越大，说明其被判别器判定为负样本的概率越接近 1，即这一项越大越好。

判别器目标函数的最大值代表的是真实数据分布与生成数据分布的 JS 散度，JS 散度可以衡量分布的相似性（当两个分布没有重叠部分时，JS 散度变为常数，这会使得梯度变为 0，造成梯度消失的问题）。

如果判别网络参数 $\mathbf{\phi }$ 固定，那么可以通过最小化以下目标函数学习生成网络参数 $\mathbf{\theta }$，使其具有以假乱真地生成数据的能力。
$$\underset{\mathbf{\theta }}{\min }\{E_{\mathbf{z}\sim P_{\text{seed}}(\mathbf{z})}[\log (1-D(G(\mathbf{z};\mathbf{\theta });\bar{\mathbf{\phi }}))]\}$$ 该项越小，即表示生成数据被判别器判定为负样本的概率越接近 0，判别器将生成样本当作了真实数据。

判别网络和生成网络形成博弈关系，可以定义以下的极小极大问题，也就是 GAN 的学习目标函数：
$$\underset{\mathbf{\theta }}{\min }\underset{\mathbf{\phi }}{\max }\{E_{\mathbf{x}\sim P_{\text{data}}(\mathbf{x})}[\log D(\mathbf{x};\mathbf{\phi })]+E_{\mathbf{z}\sim P_{\text{seed}}(\mathbf{z})}[\log (1-D(G(\mathbf{z};\mathbf{\theta });\mathbf{\phi }))]\}$$

GAN 的训练

在实际训练时，不进行 $\log (1-D(G(\mathbf{z};\mathbf{\theta });\mathbf{\phi }))$ 的最小化，而是进行 $\log D(G(\mathbf{z};\mathbf{\theta });\mathbf{\phi })$ 的最大化。这是因为在学习的初始阶段，生成网络较弱，判别网络很容易区分训练数据和生成数据，最小化 $\log (1-D(G(\mathbf{z};\mathbf{\theta });\mathbf{\phi }))$ 会使学习很难进行下去。因此，判别网络和生成网络的学习都使用梯度上升法。

判别网络训练时从训练数据和生成数据中同采样 $M$ 个样本，判别网络学习迭代 $S$ 次后，生成网络学习迭代 1 次，这样可以保证训练判别网络有足够能力时再训练生成网络。$M$ 和 $S$ 是超参数，要在具体应用中调节。

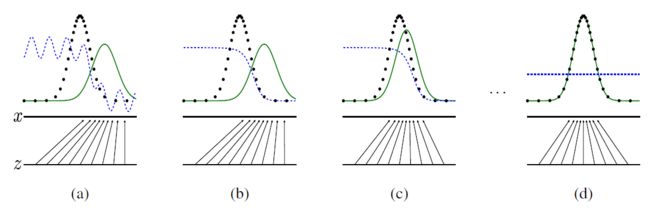
下图是原论文（Generative Adversarial Networks）中作者给出的 GAN 的学习过程。下面的横线代表生成网络输入 $\mathbf{z}$ 的分布，这里假设是均匀分布。中间横线表示生成网络输出 $\mathbf{x}$ 的分布。两条横线之间的有向实线表示生成网络的映射。上面黑色点线表示真实数据分布，绿色实线表示生成数据分布，蓝色点线表示判别网络的判别分布。训练初始，生成数据分布和真实数据分布相差较远，判别网络的判别概率也不准确（a）；生成网络固定，判别网络训练后，其判别概率有所提升（b）；判别网络固定，生成网络训练后，其生成数据分布和真实数据分布趋于接近（c）；训练收敛后，生成网络达到最优，判别网络也达到最优，对任意样本的判别概率都为 0.5.

模式崩溃

GAN 在训练时还会出现所谓的模式崩溃，即某个模式出现大量样本，缺乏多样性（生成器变懒，宁愿只生成一些简单重复的样本，这样很安全，惩罚较小）。

针对模式崩溃的解决方案：

针对目标函数的改进方法

UnrolledGAN：在更新生成器时会更新 $k$ 次生成器，参考的损失值不是某一次的损失值，而是判别器 $k$ 次迭代后的损失值。判别器后面的 $k$ 次迭代不更新自己的参数，只计算损失值用于更新生成器。这种方式使得生成器考虑到了后面 $k$ 次判别器的变化情况，即给予生成器一些预见性来做出最优解。

针对网络架构的改进方法

多智能自主体对抗生成网络（multi agent diverse GAN，MAD-GAN）采用多个生成器、一个判别器以保障样本生成的多样性，且在设计损失函数的时候，加入一个正则项，正则项中使用余弦距离来惩罚不同生成器生成样本的一致性。

小批量判别

小批量判别在判别器的中间层建立一个小批量层用于计算基于 $L_1$ 距离的样本统计量，通过建立该统计量去计算一个批次内某个样本与其他样本的接近程度。这个信息可以被判别器利用，从而甄别出那些缺乏多样性的样本。

训练崩溃

GAN 训练崩溃，指的是在训练过程中，生成器和判别器存在一方压倒另一方的情况。比如判别器太强，对于生成器生成的图片可以轻易区分，此时判别器、生成器损失值为 0，参数将不再更新。

WGAN 的作者提出使用 Wasserstein 距离，也常常叫做推土机距离，以解决 GAN 网络训练过程难以判断收敛性的问题。上面我们提到过，对于 JS 散度来说，如果两个分布没有任何重叠，那么会造成梯度消失；而对于推土机距离来说，即使两个分布没有任何重叠，也可以反映两者之间的距离，即都会有梯度。

从代码实现来说，WGAN 的改动其实就以下几点：

• 判别器最后一层去掉 sigmoid；
• 生成器和判别器的损失函数不取 log；
• 每次更新判别器的参数之后把它们的绝对值截断到不超过一个固定常数 c

下面总结了一些如何尽量避免 GAN 训练崩溃问题的解决方法：

1. 归一化图像到（-1，1）之间，生成器最后一层使用 tanh 激活函数；
2. 在训练生成器的时候，考虑反转标签；
3. 应在高斯分布上采样；
4. 一个 Mini-batch 里必须只有正样本或者负样本，不要混在一起；
5. 避免稀疏梯度，即少用 ReLU、最大池化方法；
6. 对于生成器，在训练和测试的时候使用 Dropout

---

图像生成中的应用

可以使用 GAN 技术从图像数据中学习生成网络，用于图像数据的自动生成。我们先介绍 DCGAN 及其使用的转置卷积。

DCGAN：CNN 与 GAN 的结合

转置卷积

转置卷积（transposed convolution）也称为微步卷积（fractionally strided convolution）或反卷积（deconvolution），在图像生成网络、图像自动编码器等模型中广泛使用。卷积可以用于图像数据尺寸的减小，而转置卷积可以用于图像数据尺寸的放大，又分别称为下采样和上采样。

卷积运算可以表示为线性变换。假设有核矩阵为以下矩阵 $\mathbf{W}$、填充为 0、步幅为 1 的卷积运算
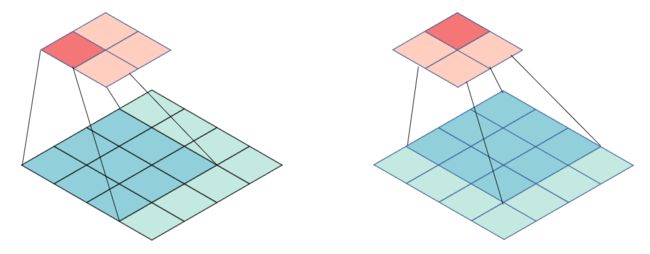
[ w 11 w 12 w 13 w 21 w 22 w 23 w 31 w 32 w 33 ] \begin{bmatrix} w_{11} & w_{12} & w_{13} \\ w_{21} & w_{22} & w_{23} \\ w_{31} & w_{32} & w_{33} \end{bmatrix} ​w11​w21​w31​​w12​w22​w32​​w13​w23​w33​​ ​ 下图显示输出矩阵前两个元素的计算过程。

假设输入矩阵的大小是 $4\times 4$，输出矩阵的大小是 $2\times 2$，这个卷积进行的是下采样。

构建矩阵 $\mathbf{C}$：
[ w 11 w 12 w 13 0 w 21 w 22 w 23 0 w 31 w 32 w 33 0 0 0 0 0 0 w 11 w 12 w 13 0 w 21 w 22 w 23 0 w 31 w 32 w 33 0 0 0 0 0 0 0 0 w 11 w 12 w 13 0 w 21 w 22 w 23 0 w 31 w 32 w 33 0 0 0 0 0 0 w 11 w 12 w 13 0 w 21 w 22 w 23 0 w 31 w 32 w 33 ] \begin{bmatrix} w_{11} & w_{12} & w_{13} & 0 & w_{21} & w_{22} & w_{23} & 0 & w_{31} & w_{32} & w_{33} & 0 & 0 & 0 & 0 & 0\\ 0 & w_{11} & w_{12} & w_{13} & 0 & w_{21} & w_{22} & w_{23} & 0 & w_{31} & w_{32} & w_{33} & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & w_{11} & w_{12} & w_{13} & 0 & w_{21} & w_{22} & w_{23} & 0 & w_{31} & w_{32} & w_{33} & 0 \\ 0 & 0 & 0 & 0 & 0 & w_{11} & w_{12} & w_{13} & 0 & w_{21} & w_{22} & w_{23} & 0 & w_{31} & w_{32} & w_{33} \end{bmatrix} ​w11​000​w12​w11​00​w13​w12​00​0w13​00​w21​0w11​0​w22​w21​w12​w11​​w23​w22​w13​w12​​0w23​0w13​​w31​0w21​0​w32​w31​w22​w21​​w33​w32​w23​w22​​0w33​0w23​​00w31​0​00w32​w31​​00w33​w32​​000w33​​ ​ 每一行表示在每一个位置的卷积操作。

考虑基于矩阵 $\mathbf{C}$ 的线性变换，其输入是输入矩阵展开的向量，输出是输出矩阵展开的向量。这个线性变换对应神经网络前一层到后一层的信号传递。

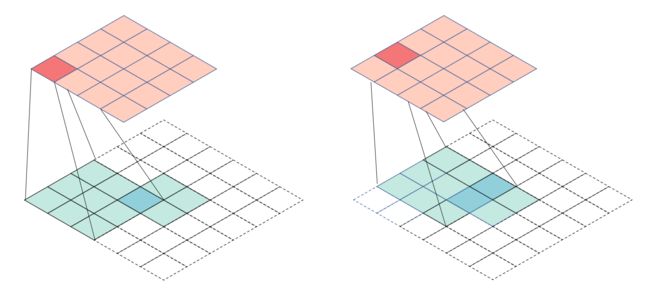
另一方面，考虑基于转置矩阵 ${\mathbf{C}}^{\top }$ 的线性变换，这个线性变换对应神经网络后一层到前一层的信号传递。事实上，存在另一个卷积运算，表示在基于转置矩阵 ${\mathbf{C}}^{\top }$ 的线性变换中，其核矩阵为以下矩阵：
rot180 ( W ) = [ w 33 w 32 w 31 w 23 w 22 w 21 w 13 w 12 w 11 ] \text{rot180}(\bm{W})=\begin{bmatrix} w_{33} & w_{32} & w_{31} \\ w_{23} & w_{22} & w_{21} \\ w_{13} & w_{12} & w_{11} \end{bmatrix} rot180(W)= ​w33​w23​w13​​w32​w22​w12​​w31​w21​w11​​ ​ 称这个卷积为转置卷积。这个转置卷积是核矩阵为 $\text{rot180}(\mathbf{W})$、填充为 2、步幅为 1 的卷积运算。下图显示以上转置卷积计算的过程，输入矩阵大小是 $2\times 2$，输出矩阵的大小是 $4\times 4$，转置卷积进行的是上采样。

DCGAN

如果使用原始的基于 DNN 的 GAN，在视觉任务上会出现很多问题。如果输入 GAN 的随机噪声为 100 维的随机噪声，输出图像大小为 $256\times 256$，也就是说，要将 100 维的信息映射为 65536 维，如果单纯用 DNN 来实现，整个模型参数会非常巨大。

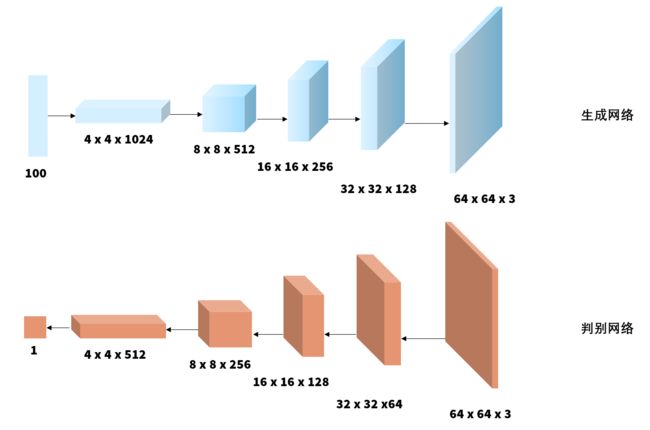
深度卷积生成对抗网络（deep convolutional generative adversarial networks，DCGAN）和其他 GAN 模型一样由生成网络和判别网络组成。下图给出 DCGAN 的架构，用特征图表示各层的卷积运算。DCGAN 的学习算法和 GAN 的算法完全一样，但包含一些实现上的技巧。

DCGAN 的生成网络和判别网络有以下特点：

• 生成网络使用转置卷积进行上采样，判别网络使用卷积进行下采样；
• 生成网络和判别网络都没有汇聚层；
• 生成网络和判别网络都没有全连接的隐层；
• 生成网络的激活函数除输出层使用 tanh，其他层均使用 ReLU；
• 判别网络的激活函数除输出层使用 S 型函数以外，其他层均使用 Leaky ReLU；
• 生成网络和判别网络的学习都采用批量归一化；
• 生成网络和判别网络的所有卷积层的卷积核尺寸都是 5，步幅都是 2

---

CGAN：生成指定类型的图像

条件生成对抗网络（CGAN）在一定程度上解决了 GAN 生成结果的不确定性，给出了生成器在生成过程中的限制条件。CGAN 的网络结构如下图所示：

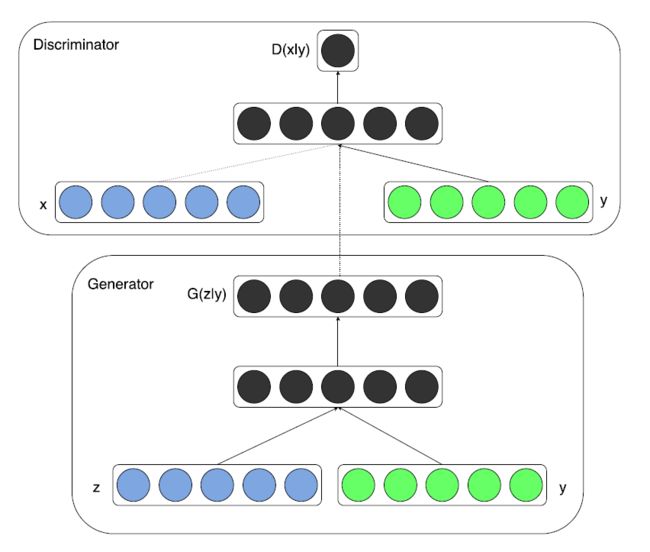
对于生成器，其输入不仅仅是随机噪声的采样 $\mathbf{z}$，还有预生成图像的标签信息。同样的，判别器的输入也包括样本的标签，这就使得判别器和生成器可以学习到样本和标签之间的联系。

损失函数设计和原始 GAN 基本一致，只不过生成器、判别器的输入数据是一个条件分布。具体编程实现时只需要对随机噪声采样 $\mathbf{z}$ 和输入条件 $\mathbf{y}$ 做一个级联即可。

---

图像翻译中的应用

图像翻译是指从一幅图像到另一幅图像的转换，就像机器翻译中一种语言转换为另一种语言。常见的图像翻译任务有图像去噪、图像超分辨、图像补全、风格迁移等。

图像翻译可以分为以下两种：

1. 有监督图像翻译：原始域与目标域存在一一对应数据；
2. 无监督图像翻译：原始域与目标域不存在一一对应数据

pix2pix：有监督图像翻译

上图展示了一些有趣的结果，比如分割图→街景图，边缘图→真实图。对于这类图像翻译问题，最简单的做法就是设计一个 CNN 网络，直接建立输入→输出的映射，可对于上面的问题，这样做会带来生成图像质量不清晰的问题。

如何解决生成图像的模糊问题？作者想了一个办法，即加入 GAN 的损失函数去惩罚模型。在上述想法的基础上加入一个判别器，判断输入图片是否是真实样本。pix2pix 模型训练示意图如下所示：

pix2pix 的本质为一个 CGAN，$x$ 作为此 CGAN 的条件，需要输入到 $G$ 和 $D$ 中。$G$ 的输入是 $x,z$（其中 $x$ 是需要转换的图片，$z$ 是随机噪声），输出是生成的图片 $G(x,z)$。$D$ 则需要判别真假。最终的损失函数由两部分组成：

• 输出和标签信息的 $L_1$ 损失函数；
• GAN 的损失函数

如原论文所述，我们需要应用随机抖动和镜像来预处理训练集：

• 将每个 256 x 256 图像调整为更大的高度和宽度，286 x 286；
• 将其随机裁剪回 256 x 256；
• 随机水平翻转图像，即从左到右（随机镜像）；
• 将图像归一化到 [-1, 1] 范围

生成器是经过修改的 U-Net。U-Net 由编码器（下采样器）和解码器（上采样器）构成：

• 编码器中的每个块为：Convolution -> Batch normalization -> Leaky ReLU；
• 解码器中的每个块为：Transposed convolution -> Batch normalization -> Dropout（应用于前三个块）-> ReLU；
• 编码器和解码器之间存在跳跃连接（如在 U-Net 中）

判别器是一个卷积 PatchGAN 分类器，它会尝试对每个图像分块的真实与否进行分类：

• 判别器中的每个块为：Convolution -> Batch normalization -> Leaky ReLU；
• 最后一层之后的输出形状为 (batch_size, 30, 30, 1)；
• 输出的每个 30 x 30 图像分块会对输入图像的 70 x 70 部分进行分类，即相当于我们把输入图像分成大小为 70 x 70 的图像块，然后将这些图像块提供给判别器；
• 判别器接收 2 个输入：
  • 输入图像和目标图像，应分类为真实图像；
  • 输入图像和生成图像（生成器的输出），应分类为伪图像

---

CycleGAN：无监督图像翻译

CycleGAN 和 pix2pix 的区别在于，pix2pix 模型必须要求成对数据，而 CycleGAN 利用非成对数据也能进行训练，它相当于把一类图片转换成另一类。也就是说，现在有两个样本空间，$A$ 和 $B$，我们希望把 $A$ 空间的样本转换为 $B$ 空间的样本，实际的学习过程就是学习从 $A$ 到 $B$ 的映射 $F$。但映射 $F$ 完全可以将所有 $A$ 中的图片都映射为 $B$ 中的同一张图片，使损失无效化。

对此，作者又提出了循环一致性损失（Cycle Consistency Loss）。此时，我们再假设一个映射 $G$，它可以将 $B$ 空间中的图片转换为 $A$ 中的图片。CycleGAN 同时学习这两个映射，这就杜绝了模型把所有 $A$ 的图片都转换为 $B$ 中的同一张图片。

在循环一致损失中，

• 图片 $\mathbf{X}$ 通过生成器 $G$ 传递，该生成器生成图片 $\hat{\mathbf{Y}}$；
• 生成的图片 $\hat{\mathbf{Y}}$ 通过生成器 $F$ 传递，循环生成图片 $\hat{\mathbf{X}}$；
• 在 $\mathbf{X}$ 和 $\hat{\mathbf{X}}$ 之间计算平均绝对误差

---

References

[1] 《机器学习方法》，李航，清华大学出版社。
[2] 《深度学习500问》，谈继勇，电子工业出版社。
[3] “pix2pix: Image-to-image translation with a conditional GAN”，TensorFlow 官网。