初识线段树
初识线段树
线段树是一种二叉搜索树,与区间树相似,它将一个区间划分成一些单元区间,每个单元区间对应线段树中的一个叶结点。
使用线段树可以快速的查找某一个节点在若干条线段中出现的次数,时间复杂度为O(logN)。而未优化的空间复杂度为2N,实际应用时一般还要开4N的数组以免越界,因此有时需要离散化让空间压缩。
题目一:
现在有100000个正整数,编号从1到100000。现给定一个区间[L,R]。
求得区间L到R的总和为多少
方法一:直接for(int i=L;i<=R;i++)来遍历100000个数字,全部加起来
方法二:通过求取前缀和来简化计算,另前缀和数组为B[100010],那么结果就是B[R]-B[L-1]就是结果,不难看出来,方法二比方法一更加快
题目二:
现在有100000个正整数,编号从1到100000。
现给定一个区间[L,R]和一个正整数k,c。
将第k个数加上c之后,对区间L到R求其总和
如果继续使用方法一它的时间复杂度是不会变化的。
但对于方法二来说,加了一个数之后,它的前缀和数组就要发生改变了,假如k=10,那么[10,100000]这整段区间的前缀和全部都需要修改,这就会大大降低计算速度
从上面的两个例子可以看出来
方法一:求和慢,但修改很快
方法二:求和快,但求和很慢
那么有没有一种方法可以兼顾这两种方法的优点呢,求和以及修改都快,这就是这篇要介绍的线段树了,线段数的插入的时间复杂度都是logN
线段树的划分
线段树是一颗二叉树,给定一个区间[L,R]之后,我们不断将区间平分,直到L==R。
如何定义一个线段树
由图可知,线段树是由很多个区间组成的,每一个区间都记录了区间的左端点和右端点,以及区间内的数值之和,所以我们需要定义一个结构体
struct node
{
int l, r;
int sum;
}tr[4*N];
数组大小需要开四倍,原因就不证明了,先记住即可
如何计算每个区间的值呢?
自下而上计算
可以从线段树的叶子节点(只有自己的节点),比如区间[1,2]可以通过计算node[i].l+node[i].r(1+2)。
从下往上依次计算。
void push_up(int u)
{
tr[u].sum = tr[2 * u].sum + tr[2 * u + 1].sum;//2*u为左儿子,2*u+1为右儿子
}
如何建立起一个线段树呢?
void build(int u, int l, int r)
{
if (l == r) tr[u] = { l,r ,w[l]};//如果达到了叶子节点,就赋值
else
{
tr[u] = { l,r };//没有到达叶子节点,就先记录下当前区间的左端点和右端点
int mid = l + r >> 1;//将区间平分
build(2 * u, l, mid);//递归左儿子
build(2 * u + 1, mid + 1, r);//递归右儿子
push_up(u);//回溯的时候依次通过左右儿子算得sum
}
}
如何对某个值进行修改呢?
void modify(int u, int x, int v)
{
if (tr[u].l == tr[u].r)//递归到了叶子节点的时候
{
tr[u].sum += v;
return;
}
else
{
int mid = (tr[u].l + tr[u].r) / 2;
if (x <= mid) modify(u * 2, x, v);//如果当前序列在左边,那么就递归左区间
else modify(u * 2 + 1, x, v);//在右边就递归右区间
push_up(u);//修改了之后,还要需要修改一些节点的值,重新自下而上计算
}
}
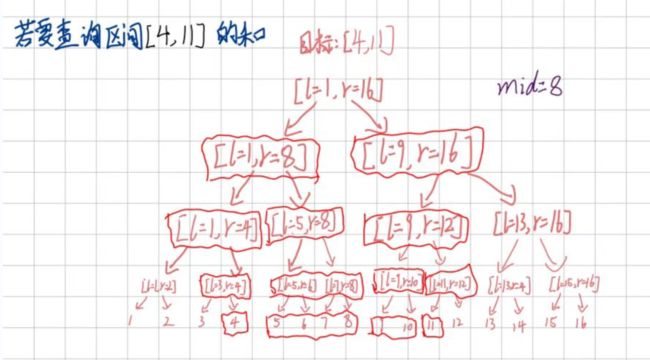
如何求得某个区间的和呢?
需要设计到的区间有[4],[5,6],[7,8],[9,10],[11]。
int query(int u, int l, int r)
{
//需要累加所有在这个范围内的区间
if (l <= tr[u].l && r >= tr[u].r) return tr[u].sum;
//否则的话就需要递归计算
int mid = (tr[u].l + tr[u].r) / 2;
int sum = 0;
if (mid >= l) sum += query(u*2, l, r);//如果左区间和要求的区间有交集,那么递归左区间
if (r >= mid + 1) sum += query(u * 2 + 1, l, r);//如果右区间和要求的区间有交集,那么递归右区间
return sum;
}
经典例题:
AC代码:
#include
using namespace std;
const int N = 100010;
int n, m;
int w[N];//权值
//定义线段树节点
struct node
{
int l, r;
int sum;
}tr[4*N];//要开四倍大小
//向上累加
void push_up(int u)
{
tr[u].sum = tr[2 * u].sum + tr[2 * u + 1].sum;
}
//建树
void build(int u, int l, int r)
{
if (l == r) tr[u] = { l,r ,w[l]};//如果达到了叶子节点,就赋值
else
{
tr[u] = { l,r };//没有到达叶子节点,就先记录下当前区间的左端点和右端点
int mid = l + r >> 1;//将区间平分
build(2 * u, l, mid);//递归左儿子
build(2 * u + 1, mid + 1, r);//递归右儿子
push_up(u);//回溯的时候依次通过左右儿子算得sum
}
}
//区间查询
int query(int u, int l, int r)
{
//需要累加所有在这个范围内的区间
if (l <= tr[u].l && r >= tr[u].r) return tr[u].sum;
//否则的话就需要递归计算
int mid = (tr[u].l + tr[u].r) / 2;
int sum = 0;
if (mid >= l) sum += query(u*2, l, r);//如果左区间和要求的区间有交集,那么递归左区间
if (r >= mid + 1) sum += query(u * 2 + 1, l, r);//如果右区间和要求的区间有交集,那么递归右区间
return sum;
}
//修改
void modify(int u, int x, int v)
{
if (tr[u].l == tr[u].r)//递归到了叶子节点的时候
{
tr[u].sum += v;
return;
}
else
{
int mid = (tr[u].l + tr[u].r) / 2;
if (x <= mid) modify(u * 2, x, v);//如果当前序列在左边,那么就递归左区间
else modify(u * 2 + 1, x, v);//在右边就递归右区间
push_up(u);//修改了之后,还要需要修改一些节点的值,重新自下而上计算
}
}
int main(void)
{
cin >> n >> m;
for (int i = 1; i <= n; i++) scanf("%d", &w[i]);
build(1, 1, n);
while (m--)
{
int k, a, b;
cin >> k >> a >> b;
if (k == 0) cout << query(1, a, b) << endl;
else
{
modify(1, a, b);
}
}
return 0;
}
没有完全AC代码(太慢了):
#include
#include
using namespace std;
const int N = 100010;
int w[N];
int n, m;
struct node
{
int l,r;
int maxv;
}tr[N*4];
void push_up(int u)
{
tr[u].maxv = max(tr[u * 2].maxv, tr[u * 2 + 1].maxv);
}
void build(int u, int l, int r)
{
if (l == r)
{
tr[u] = { l,r,w[l] };
return;
}
else
{
tr[u] = { l,r};
int mid = (l + r) >> 1;
build(u * 2, l, mid);
build(u * 2 + 1, mid+1, r);
push_up(u);
}
}
int query(int u, int l, int r)
{
if (tr[u].l >= l && tr[u].r <= r) return tr[u].maxv;
int mid = (tr[u].l + tr[u].r) / 2;
int maxv = -10000000;
if (l <= mid) maxv = max(maxv, query(u * 2, l, r));
if (r > mid + 1) maxv = max(maxv, query(u * 2 + 1, l, r));
return maxv;
}
int main()
{
int l, r;
scanf("%d %d", &n, &m);
for (int i = 1; i <= n; ++i) scanf("%d", &w[i]);
build(1, 1, n);
while (m--) {
scanf("%d %d", &l, &r);
printf("%d\n", query(1, l, r));
}
return 0;
}