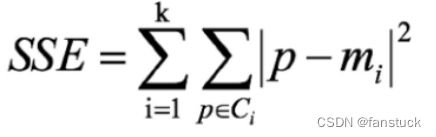一文速学数模-K-means聚类算法实战：信用卡用户画像聚类分析

目录

前言

一、用户画像概述

1.用户画像

2.为何用聚类算法作用户画像

二、数据质量校验

1.数据背景

2.数据说明

三、数据预处理

1.数据空缺值检验

 2.数据归一化

四、K-means聚类

step1:选取K值

手肘法

step2:计算初始化K点

step3:迭代计算重新划分

五.画像分析

---

前言

该项目算是非常经典的金融业务用户画像的基础分析了，主要根据用户信用卡使用行为数据进行分析，根据收集到的不同字段信息，对每个用户划分类别。这里需要说明一下的是，聚类模型只是将具有相似行为的大部分用户聚集到一个类别里面，这点并不会考虑到每个字段的含义，也就是分成的类别并不是用户价值等级，此类别仅仅是这个类别大体相同的信用卡用户行为对象，并不能给每个用户价值打上标签，那是评价模型做的事，这里要注意不要搞混淆了，用户价值评价是评价模型决定的，而画像是聚类模型分析的。

博主专注建模四年，参与过大大小小数十来次数学建模，理解各类模型原理以及每种模型的建模流程和各类题目分析方法。此专栏的目的就是为了让零基础快速使用各类数学模型以及代码，每一篇文章都包含实战项目以及可运行代码。博主紧跟各类数模比赛，每场数模竞赛博主都会将最新的思路和代码写进此专栏以及详细思路和完全代码。希望有需求的小伙伴不要错过笔者精心打造的专栏。

以下是整篇文章内容。

---

一、用户画像概述

数据分析主要是根据用户行为以及不同的业务情况去分析，而用户画像的需求是我们首先需要了解的建模场景。什么是用户画像？为什么要建立用户画像，怎么去建立？这需要我们先了解这一点，才好方便建模。

1.用户画像

用户画像是指根据用户的属性、用户偏好、生活习惯、用户行为等信息而抽象出来的标签化用户模型。通俗说就是给用户打标签，而标签是通过对用户信息分析而来的高度精炼的特征标识。通过打标签可以利用一些高度概括、容易理解的特征来描述用户，可以让人更容易理解用户，并且可以方便计算机处理。简单来说就是：利用已经获得的数据，勾勒出用户需求、用户偏好的一种运营工具和数据分析方法。

 根据用户画像的作用可以看出，用户画像的使用场景较多，用户画像可以用来挖掘用户兴趣、偏好、人口统计学特征，主要目的是提升营销精准度、推荐匹配度，终极目的是提升产品服务，起到提升企业利润。用户画像适合于各个产品周期：从新用户的引流到潜在用户的挖掘、从老用户的培养到流失用户的回流等。

2.为何用聚类算法作用户画像

聚类算法是一种常用的无监督学习算法，可以将具有相似特征的数据点归为一类。在用户画像中，聚类算法可以将相似的用户归为一组，从而为营销策略、产品设计和推荐系统等提供有价值的信息。

以下是使用聚类算法作用户画像的一些好处：

1. 识别用户群体：聚类算法可以将用户数据聚类成不同的群体，这有助于识别不同的用户群体，为营销策略提供有价值的信息。

2. 了解用户偏好：聚类算法可以将具有相似特征的用户聚类在一起，从而了解用户的偏好和需求。这可以帮助企业根据用户的喜好和需求开发相应的产品或服务，提高用户满意度。

3. 个性化推荐：聚类算法可以将用户划分为不同的群体，为个性化推荐提供有价值的信息。基于用户画像，企业可以向用户提供更加符合其喜好和需求的产品或服务，从而提高用户满意度和忠诚度。

4. 精细化运营：基于用户画像，企业可以根据用户的需求和行为开展精细化运营，提高用户留存率和复购率。

二、数据质量校验

在了解了上述用户画像的作用之后，我们需要对我们拿到的数据进行分析，这里我采用的是kaggle信用卡用户行为数据。

1.数据背景

信用卡营销就是指通过激发和挖掘人们对信用卡商品的需求，设计和开发出满足持卡人需求的信用卡商品，并且通过各种有效的沟通手段使持卡人接受并使用这种商品，从中获得自身最大的满足，以实现经营者的目标。 对于不同的客户群体，需要采用不同的营销手段，因此需要对客户进行分组聚类。

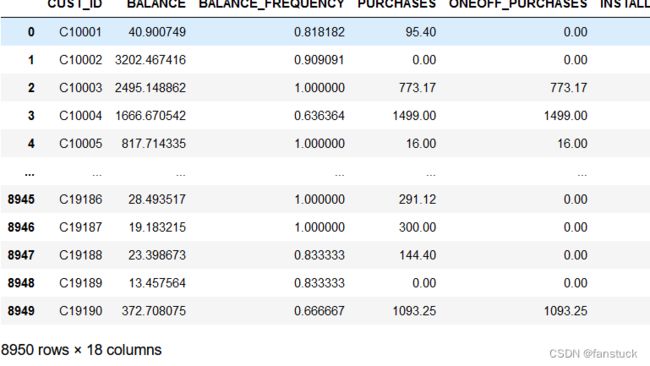
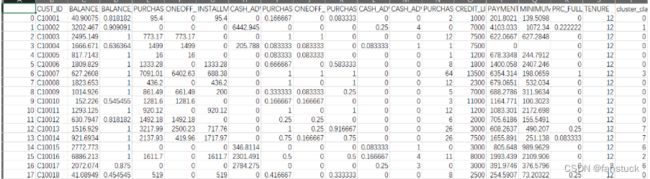
2.数据说明

该文件位于具有18个行为变量的客户级别。

1. CUST_ID：信用卡持有人的身份证明（分类）

2. BALANCE：他们帐户中剩余的余额可用于购买

3. BALANCE_FREQUENCY：更新余额的频率，得分在0到1之间（1 =频繁更新，0 =不频繁更新）

4. PURCHASES：通过帐户购买的金额

5. ONEOFF_PURCHASES：一次性购买的最大金额

6. INSTALLMENTS_PURCHASES：分期购买的金额

7. CASH_ADVANCE：用户预先提供的现金

8. PURCHASES_FREQUENCY：进行购买的频率，得分在0到1之间（1 =频繁购买，0 =不频繁购买）

9. ONEOFFPURCHASESFREQUENCY：一次购买的频率（1 =频繁购买，0 =不频繁购买）

10. PURCHASESINSTALLMENTSFREQUENCY：分期购买的频率（1 =频繁执行，0 =不频繁执行）

11. CASHADVANCEFREQUENCY：多长时间支付一次预付款

12. CASHADVANCETRX：使用“高级现金”进行的交易数量

13. PURCHASES_TRX：进行的购买交易数

14. CREDIT_LIMIT：用户的信用卡限额

15. PAYMENTS：用户完成的付款金额

16. MINIMUM_PAYMENTS：用户的最低付款金额

17. PRCFULLPAYMENT：用户支付的全额付款的百分比

18. TENURE：用户的信用卡服务的使用权

 为了更加直观的去作用户画像，这里我仅选择偏业务的正向数据进行建模，当然聚类并不是挖掘客户的消费潜力价值，我这里选择正向特征仅是为了更直观的进行画像描述，除去偏业务方向的知识，仅对画像建立过程优化。

根据特征字段，我们需要选定建模需要的字段信息，若为正向指标则越大越好：

1.BALANCE：帐户中剩余的余额可用于购买，那么该数值越大，用户购买能力越大，正向指标 1

2.BALANCE_FREQUENCY：更新余额的频率 正向指标 1

3.PURCHASES：通过帐户购买的金额 正向指标 1

4.ONEOFF_PURCHASES：一次性购买的最大金额 正向指标 1

5.INSTALLMENTS_PURCHASES：分期购买的金额 正向指标 1

6.CASH_ADVANCE：用户预先提供的现金 正向指标 1

7.PURCHASES_FREQUENCY：进行购买的频率，得分在0到1之间（1 =频繁购买，0 =不频繁购买）正向指标 1

8.ONEOFFPURCHASESFREQUENCY 一次购买的频率（1 =频繁购买，0 =不频繁购买）正向指标 1

9.PURCHASESINSTALLMENTSFREQUENCY：分期购买的频率（1 =频繁执行，0 =不频繁执行）中向指标 与上一个指标互斥

10.CASHADVANCEFREQUENCY：多长时间支付一次预付款 负向指标0

11.CASHADVANCETRX：使用“高级现金”进行的交易数量 正向指标 1

12.PURCHASES_TRX：进行的购买交易数 正向指标 1

13.CREDIT_LIMIT：用户的信用卡限额 正向指标 1

14.PAYMENTS：用户完成的付款金额 正向指标 1

15.MINIMUM_PAYMENTS：用户的最低付款金额 中性指标

16.PRCFULLPAYMENT：用户支付的全额付款的百分比 正向指标1

数据差异很大，我们尽可能拿出所有可用到的正向指标聚类，那么高纬度的用户群体就是重要价值用户。

三、数据预处理

1.数据空缺值检验

df_data.isnull().sum()

 

CUST_ID                               0
BALANCE                               0
BALANCE_FREQUENCY                     0
PURCHASES                             0
ONEOFF_PURCHASES                      0
INSTALLMENTS_PURCHASES                0
CASH_ADVANCE                          0
PURCHASES_FREQUENCY                   0
ONEOFF_PURCHASES_FREQUENCY            0
PURCHASES_INSTALLMENTS_FREQUENCY      0
CASH_ADVANCE_FREQUENCY                0
CASH_ADVANCE_TRX                      0
PURCHASES_TRX                         0
CREDIT_LIMIT                          1
PAYMENTS                              0
MINIMUM_PAYMENTS                    313
PRC_FULL_PAYMENT                      0
TENURE                                0
dtype: int64

 空缺处理方法有很多种，大家可以去看我的另一篇文章：

一文速学(四)-数据分析Pandas处理缺失值操作各类方法详解

这些数据基本全为定量数据，可以直接使用机器学习算法对空缺值进行填充，这里使用随机森林填补：

# 随机森林填补缺失值
from sklearn.ensemble import RandomForestRegressor   
RF = RandomForestRegressor()
paymentsNotNull = df_data.MINIMUM_PAYMENTS.notnull()
columns = ['BALANCE','BALANCE_FREQUENCY','PURCHASES','ONEOFF_PURCHASES','INSTALLMENTS_PURCHASES','CASH_ADVANCE','PURCHASES_FREQUENCY','ONEOFF_PURCHASES_FREQUENCY','PURCHASES_INSTALLMENTS_FREQUENCY','CASH_ADVANCE_FREQUENCY','CASH_ADVANCE_TRX','PURCHASES_TRX','PAYMENTS']
RF.fit(df_data.loc[paymentsNotNull,columns],df_data.MINIMUM_PAYMENTS[paymentsNotNull])
print(RF.score(df_data.loc[paymentsNotNull,columns],df_data.MINIMUM_PAYMENTS[paymentsNotNull]))

分数还是不错的 ，可以达到90.8%：

# 填充
for data in [df_data]:
    pred = RF.predict(data.loc[:,columns])
    IsNull = data.MINIMUM_PAYMENTS.isnull()
    data.MINIMUM_PAYMENTS[IsNull]=pred[IsNull]

 这样就填充完毕了：

 2.数据归一化

这些数值类型数据最好进行归一化，关于归一化的所有处理步骤都有在我的另一篇博客整理：

一文速学-数据预处理归一化详细解释

我这里采用的z-score作为归一化函数：

from sklearn.preprocessing import StandardScaler  # 标准化工具
scaler = StandardScaler()
for n in range(1,14):
    x_train = scaler.fit_transform(df_true_data.iloc[:,n:n+1].values)
    df_true_data.iloc[:,n:n+1]=x_train

 得到归一化数据集，那么开始聚类建模。

四、K-means聚类

K-means的基础原理在我专栏里面有详解，需要温故一下的可以看这篇文章：

一文速学数模-聚类模型(一)K-means聚类算法详解+Python代码实例

 具体建模框架以及流程：

step1:选取K值

k 的选择一般是按照实际需求进行决定，或在实现算法时直接给定 k 值。这是基于项目你想要聚类的个数来决定的，但是也有不确定的情况，我们可能需要去一个最优的K值来将数据很好的归类达到最大化区分类别，这时候就需要思考从数据角度出发，应该进行怎么样的计算能够得到最优的K。

手肘法

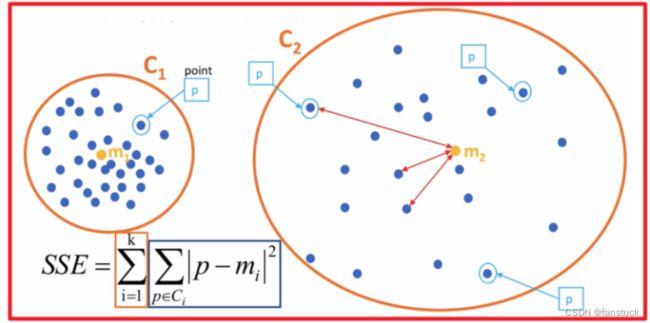
手肘法是最常用的确定K-means算法K值的方法，所用到的衡量标准是SSE（sum of the squared errors，误差平方和） 。

 SEE各个计算在K-means里含义如下图：

 

误差平方和又称残差平方和，根据n个观察值拟合适当的模型后，余下未能拟合部份()称为残差，其中y平均表示n个观察值的平均值，所有n个残差平方之和称误差平方和。

在回归分析中通常用SSE表示，其大小用来表明函数拟合的好坏。将残差平方和除以自由度n-p-1(其中p为自变量个数)可以作为误差方差σ2的无偏估计，通常用来检验拟合的模型是否显著也用来寻找K值。

import matplotlib.pyplot as plt
import pandas as pd
from sklearn.metrics import silhouette_score
from sklearn.cluster import KMeans
data=df_true_data.iloc[:,1:]
distortions=[]#簇内误差平方和  SSE
for i in range(2,15):
    Kmeans_model=KMeans(n_clusters=i)
    predict_=Kmeans_model.fit_predict(data)
    distortions.append(Kmeans_model.inertia_)
    print("簇内误差平方和：",distortions)
#SSE  手肘法
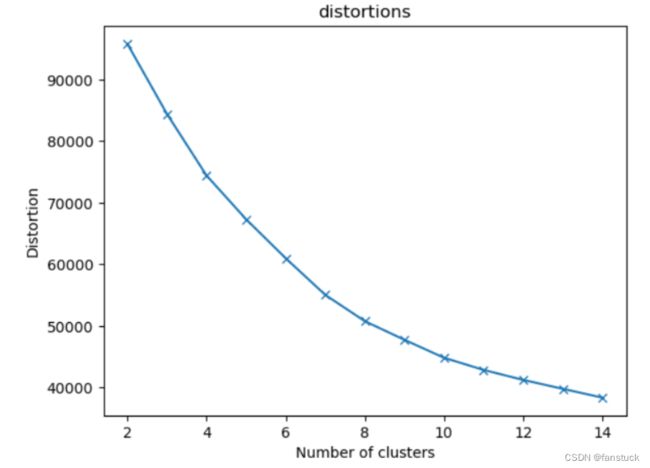
plt.plot(range(2,15),distortions,marker='x')
plt.xlabel('Number of clusters')
plt.ylabel('Distortion')
plt.title('distortions')
plt.show()

 簇内误差平方和： [95795.9293255097, 84414.58708674107, 74423.36972115413, 67317.01104077617, 60994.96414080261, 55045.26807434524, 50777.37404069404, 47753.98868450008, 44842.179122758884, 42867.62108059854, 41247.78745541904, 39800.985182972385, 38372.77525889944]

 

 根据拟合图片我们知道选K为8时能够得到最效率的K值。

step2:计算初始化K点

初始质心随机选择即可，每一个质心为一个类。对剩余的每个样本点，计算它们到各个质心的欧式距离，并将其归入到相互间距离最小的质心所在的簇。

def euclDistance(x1, x2):
    return np.sqrt(sum((x2 - x1) ** 2))
def initCentroids(data, k):
    numSamples, dim = data.shape
    # k个质心，列数跟样本的列数一样
    centroids = np.zeros((k, dim))
    # 随机选出k个质心
    for i in range(k):
        # 随机选取一个样本的索引
        index = int(np.random.uniform(0, numSamples))
        # 作为初始化的质心
        centroids[i, :] = data[index, :]
    return centroids

step3:迭代计算重新划分

• 计算各个新簇的质心。

• 在所有样本点都划分完毕后，根据划分情况重新计算各个簇的质心所在位置，然后迭代计算各个样本点到各簇质心的距离，对所有样本点重新进行划分

• 重复2. 和 3.，直到质心不在发生变化时或者到达最大迭代次数时

# 传入数据集和k值
def kmeans(data, k):
    # 计算样本个数
    numSamples = data.shape[0]
    # 样本的属性，第一列保存该样本属于哪个簇，第二列保存该样本跟它所属簇的误差
    clusterData = np.array(np.zeros((numSamples, 2)))
    # 决定质心是否要改变的质量
    clusterChanged = True
    # 初始化质心
    centroids = initCentroids(data, k)
    while clusterChanged:
        clusterChanged = False
        # 循环每一个样本
        for i in range(numSamples):
            # 最小距离
            minDist = 100000.0
            # 定义样本所属的簇
            minIndex = 0
            # 循环计算每一个质心与该样本的距离
            for j in range(k):
                # 循环每一个质心和样本，计算距离
                distance = euclDistance(centroids[j, :], data[i, :])
                # 如果计算的距离小于最小距离，则更新最小距离
                if distance < minDist:
                    minDist = distance
                    # 更新最小距离
                    clusterData[i, 1] = minDist
                    # 更新样本所属的簇
                    minIndex = j
            # 如果样本的所属的簇发生了变化
            if clusterData[i, 0] != minIndex:
                # 质心要重新计算
                clusterChanged = True
                # 更新样本的簇
                clusterData[i, 0] = minIndex
        # 更新质心
        for j in range(k):
            # 获取第j个簇所有的样本所在的索引
            cluster_index = np.nonzero(clusterData[:, 0] == j)
            # 第j个簇所有的样本点
            pointsInCluster = data[cluster_index]
            # 计算质心
            centroids[j, :] = np.mean(pointsInCluster, axis=0)
    return centroids, clusterData

 最后得到聚类结果。

五.画像分析

可以通过数据可视化横向和纵向对每个类别进行分析，由于我们之前做过特征方向标注，故进行类别分析的时候更好对每个类别用户画像区分：

比如分析聚类0：

BALANCE                     mean    545.247537
BALANCE_FREQUENCY           mean      0.827954
PURCHASES                   mean    462.690070
ONEOFF_PURCHASES            mean    212.797808
INSTALLMENTS_PURCHASES      mean    250.254275
CASH_ADVANCE                mean    207.813824
PURCHASES_FREQUENCY         mean      0.487740
ONEOFF_PURCHASES_FREQUENCY  mean      0.141411
CASH_ADVANCE_TRX            mean      1.243806
PURCHASES_TRX               mean      9.470777
PAYMENTS                    mean    677.884833
PRC_FULL_PAYMENT            mean      0.176594
TENURE                      mean     11.435975

 从均值进行分析，结合特征即可。

---