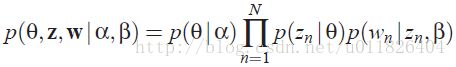LDA主题模型
概率图模型LDA(Latent Dirichlet Allocation)用于推测文档的主题分布。它将文档集中的每篇文档的主题以概率分布的形式给出,从而通过分析一些文档抽取出它们的主题分布后,便可以根据主题分布进行主题聚类或文本分类。
1. 基础知识
1.1 LDA属于贝叶斯模型
LDA是基于贝叶斯模型的,涉及到贝叶斯模型离不开“先验分布”,“数据(似然)”和"后验分布"三块:
后 验 分 布 = 先 验 分 布 + 数 据 ( 似 然 ) 后验分布 = 先验分布 + 数据(似然) 后验分布=先验分布+数据(似然)
We describe latent Dirichlet allocation (LDA), a generative probabilistic model for collections of discrete data such as text corpora.
LDA is a three-level hierarchical Bayesian model, in which each item of a collection is modeled as a finite mixture over an underlying set of topics. Each topic is, in turn, modeled as an infinite mixture over an underlying set of topic probabilities.
1.2 LDA采用词袋模型构造成词向量
在LDA中,每篇文章是用词袋模型构造成词向量。词袋模型,顾名思义,就是将文本视为一个 “装满词的袋子” ,袋子里的词语是随便摆放的,没有顺序和语义之分。在词袋模型中,“我喜欢你”和“你喜欢我”是等价的。
与词袋模型相反的一个模型是n-gram,n-gram考虑了词汇出现的先后顺序。
1.3 共轭分布
在贝叶斯概率理论中,如果后验概率P(θ|x)和先验概率p(θ)的形式一样(满足同样的分布律),那么,先验分布和后验分布被叫做共轭分布。
共轭分布的提出背景:
一方面符合人的直观,另一方面可以形成一个先验链,即现在的后验分布可以作为下一次计算的先验分布,如果形式相同,就可以形成一个链条。
比如你对好人和坏人的认知
- 先验分布为:100个好人和100个的坏人,即你认为好人坏人各占一半;
- 现在你被2个好人(数据)帮助了和1个坏人骗了,于是你得到了新的后验分布为:102个好人和101个的坏人;
- 现在你的后验分布里面认为好人比坏人多了。这个后验分布接着又变成你的新的先验分布;
- 当你被1个好人(数据)帮助了和3个坏人(数据)骗了后,你又更新了你的后验分布为:103个好人和104个的坏人;
- 依次继续更新下去。前面一次贝叶斯推荐的后验分布,又是后一次贝叶斯推荐的先验分布。也即是说,先验分布和后验分布的形式应该是一样的。
1.3 二项分布与Beta分布共轭
1.3.1 二项分布
在n重伯努利试验(n次重复独立试验,每次试验只有2种可能结果)中,若每次试验事件A出现的概率为p,则事件A出现的次数X服从参数为(n,p)的二项分布,记为 X ∼ B ( n , k ) X\sim B(n,k) X∼B(n,k)。 B i n o m ( k ∣ n , p ) = P ( X = k ) = C n k p k ( 1 − p ) n − k ( k = 0 , 1 , . . . , n ) Binom(k|n,p)=P(X=k)=C^k_np^k(1-p)^{n-k}\quad (k=0,1,...,n) Binom(k∣n,p)=P(X=k)=Cnkpk(1−p)n−k(k=0,1,...,n)二项分布的期望: E = n p E=np E=np
1.3.2 Beta分布
对于参数 α > 0 , β > 0 \alpha > 0, \beta > 0 α>0,β>0, 取值范围为[0, 1]的随机变量x的概率密度函数为: B e t a ( p ∣ α , β ) = Υ ( α ) Υ ( β ) Υ ( α + β ) p α − 1 ( 1 − p ) β − 1 Beta(p|\alpha,\beta) =\frac{\Upsilon(\alpha)\Upsilon(\beta)}{\Upsilon(\alpha+\beta)}p^{\alpha-1}(1-p)^{\beta-1} Beta(p∣α,β)=Υ(α+β)Υ(α)Υ(β)pα−1(1−p)β−1其中, Υ \Upsilon Υ是Gamma函数,是阶乘在实数集上的延拓,满足 Υ ( n ) = ( n − 1 ) ! \Upsilon(n)=(n-1)! Υ(n)=(n−1)!
Beta分布的期望: E = α α + β E=\frac{\alpha}{\alpha+\beta} E=α+βα
1.4 多项分布与Dirichlet分布共轭
1.4.1 多项分布
多项分布是二项分布在多元场合的推广。
在n次重复独立试验中,每次试验可能有若干个结果,记每次试验的可能结果为 A 1 , . . . , A r , P ( A i ) = p i , ∑ i = 1 r p i = 1 A_1,...,A_r,P(A_i)=p_i,\sum_{i=1}^r p_i=1 A1,...,Ar,P(Ai)=pi,∑i=1rpi=1。记随机变量X表示 A 1 A_1 A1出现 k 1 k_1 k1次,… , A r A_r Ar出现 k r k_r kr次,则X服从多项分布,其概率密度函数为: M u l t i ( k 1 , k 2 , . . . , k r ∣ n , p 1 , p 2 , . . . , p r ) = n ! k 1 ! k 2 ! . . . k r ! p 1 k 1 p 2 k 2 . . . p r k r Multi(k_1,k_2,...,k_r|n,p_1,p_2,...,p_r)=\frac{n!}{k_1!k_2!...k_r!}p_1^{k_1}p_2^{k_2}...p_r^{k_r} Multi(k1,k2,...,kr∣n,p1,p2,...,pr)=k1!k2!...kr!n!p1k1p2k2...prkr
1.4.2 Dirichlet分布
狄利克雷分布的概率密度函数为:
D i r i c h l e t ( p ⃗ ∣ α ⃗ ) = Γ ( ∑ k = 1 K α k ) ∏ k = 1 K Γ ( α k ) ∏ k = 1 K p k α k − 1 Dirichlet(\vec p| \vec \alpha) = \frac{\Gamma(\sum\limits_{k=1}^K\alpha_k)}{\prod_{k=1}^K\Gamma(\alpha_k)}\prod_{k=1}^Kp_k^{\alpha_k-1} Dirichlet(p∣α)=∏k=1KΓ(αk)Γ(k=1∑Kαk)k=1∏Kpkαk−1狄利克雷分布的期望: E = ( α 1 ∑ i = 1 K α i , α 1 ∑ i = 2 K α i , ⋯ , α K ∑ i = 1 K α i ) E= ( \frac{\alpha ^ 1}{\sum_{i = 1}^K \alpha_i}, \frac{\alpha ^ 1}{\sum_{i = 2}^K \alpha_i}, \cdots, \frac{\alpha ^ K}{\sum_{i = 1}^K \alpha_i} ) E=(∑i=1Kαiα1,∑i=2Kαiα1,⋯,∑i=1KαiαK)
1.5 LDA采样
在现实应用中,我们很多时候很难精确求出精确的概率分布,常常采用近似推断方法。通过使用随机化方法完成近似的采样法便是近似推断方法的一类方法。
在很多任务中,我们关心某些概率分布并非因为对这些概率分布本身感兴趣,而是要基于他们计算某些期望,并且还可能进一步基于这些期望做出决策。采样法正式基于这个思路。
假设我们的目标是计算函数 f ( x ) f(x) f(x)在概率密度函数 p ( x ) p(x) p(x)下的期望,则可根据 p ( x ) p(x) p(x)抽取一组样本 x 1 , x 2 , ⋯ , x N {x_1, x_2, \cdots, x_N} x1,x2,⋯,xN,然后计算 f ( x ) f(x) f(x)在这些样本上的均值,以此来近似目标期望 E [ f ] E[f] E[f]。基于大数定律,这种通过大量采样的办法就能获得较高的近似精度。
如何采样?
概率图模型中最常用的采样技术是马尔可夫链蒙特卡罗(MCMC)方法,先设法构造一条马尔科夫链,使其收敛至平稳分布恰为待估计参数的后验分布,然后通过这条马尔科夫链来产生符合后验分布的样本,并基于这些样本来进行估计。
这里马尔科夫链转移概率的构造至关重要,不同的构造方法将产生不同的MCMC算法。Metropolis-Hastings(简称MH)算法是MCMC的重要代表。它基于“拒绝采样”(reject sampling)来逼近平稳分布p。
2. LDA模型原理
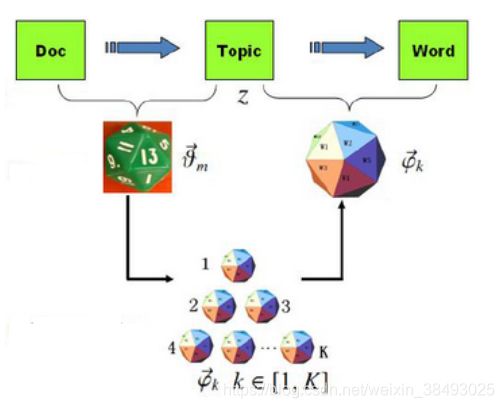
假设我们有M篇文档,对应第d个文档中有 N d N_d Nd个词。即输入为如下图所示。我们的目标是找到每一篇文档的主题分布和每一个主题中词的分布。假定主题数目为K,这样所有的分布就都基于K个主题展开。

2.1 主题数目K的确定–调参
在 LDA 中,主题的数目没有一个固定的最优解。模型训练时,需要事先设置主题数,训练人员需要根据训练出来的结果,手动调参,由优化主题数目,进而优化文本分类结果。
2.2 LDA的主要思想
LDA认为每篇文档包含多个话题,且其中每一个词都对应着一个话题,一篇文章的构造过程,首先是以一定的概率选择某个主题,然后再在这个主题下以一定的概率选出某一个词,这样就生成了这篇文章的第一个词。不断重复这个过程,就生成了整片文章。当然这里假定词与词之间是没顺序的。
LDA的使用是上述文档生成的逆过程,它将根据一篇得到的文章,去寻找出这篇文章的主题,以及这些主题对应的词。
2.3 LDA的假设条件
-
假设文档主题的先验分布是Dirichlet分布,即对于任一文档d, 其主题分布 θ d θ_d θd为: θ d = D i r i c h l e t ( α ⃗ ) \theta_d = Dirichlet(\vec \alpha) θd=Dirichlet(α)其中,α为分布的超参数,是一个K维向量。
-
假设主题中词的先验分布是Dirichlet分布,即对于任一主题k, 其词分布 β k β_k βk为:
β k = D i r i c h l e t ( η ⃗ ) \beta_k= Dirichlet(\vec \eta) βk=Dirichlet(η)其中,η为分布的超参数,是一个V维向量。V代表词汇表里所有词的个数。 -
对于数据中任意一篇文档d中的第n个词 w d n w_{dn} wdn,我们可以从主题分布 θ d θ_d θd中得到它的主题编号 z d n z_{dn} zdn的概率分布为: z d n = M u l t i ( θ d ) z_{dn} =Multi(\theta_d) zdn=Multi(θd)
-
而对于该主题编号 z d n z_{dn} zdn,我们可以从词频分布 β z d n \beta_{z_{dn}} βzdn中得到我们看到的词 w d n w_{dn} wdn的概率分布为: w d n = M u l t i ( β z d n ) w_{dn} = Multi(\beta_{z_{dn}}) wdn=Multi(βzdn)
因此可以假设文档是通过如下方式生成:
这样一个文档中的所有词都可以认为是通过话题模型来生成的,当已知一个文档的词频分布后(即一个N维向量,N为词库大小),则可以认为:每一个词频元素都对应着一个话题,而话题对应的词频分布则影响着该词频元素的大小。
2.4 LDA的联合概率函数
2.5 LDA的训练:EM算法
LDA模型主要是想从给定的输入语料中学习训练出两个控制参数α和β,当学习出了这两个控制参数就确定了模型,便可以用来生成文档。其中α和β分别对应以下各个信息:
- α:K维向量,是Dirichlet分布的参数,用于生成一个主题θ向量;
- β:各个主题对应的单词概率分布矩阵p(w|z)。
把w当做观察变量,θ和z当做隐藏变量,就可以通过EM算法学习出α和β。
3. LDA模型应用
3.1 语义表示
主题模型产生的主题分布可看做文档的语义表示,该表示能够用于文档分类、聚类、内容丰富度分析、CTR预估等多种任务。
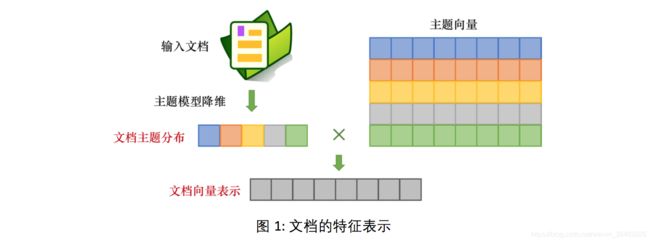
基于主题模型的文档特征表示可以分为两类,如下图所示:
- 文档主题分布:经过主题模型降维,得到文档在主题上的多项分布,LDA、SentenceLDA等模型支持这一类的文档特征表示。
由于LDA中采用文档内的Bag-of-Words假设,词与词之间的位置信息是被忽略的。在很多工业界场景中,我们往往需要限制某些位置相近的词产生自同一主题,通过SentenceLDA能很好地满足这个需求。SentenceLDA假设同一个句子里的词产生自同一主题,对句子内的词进行了进一步的建模,能捕捉到更加细粒度的共现关系。
- 文档向量表示:联合使用主题向量和文档主题分布,生成的文档向量表示,Topical Word Embedding (TWE) 等融合了词向量的主题模型可以支持这一类的文档特征表示。
LDA产生的主题往往被高频词占据,这种现象导致低频词在实际应用中的作用非常有限。TWE利用LDA训练获得的主题为词向量的训练提供补充信息,进而得到词和主题的向量表示。鉴于向量表示可以较好地建模低频词的语义信息,通过利用词和主题的向量表示,我们可以更好地捕捉每个主题下的低频词的语义信息,提升下游应用的效果。
3.1.1 新闻质量分类
对于新闻APP,其通过各种来源获得到的新闻,质量通常良莠不齐。为了提升用户体验,我们通常会构建一个分类器来自动过滤低质量的新闻。
我们可以人工设计一些传统特征:新闻来源站点、新闻内容长度、图片数量、新闻热度等等。除了这些人工特征,也可利用主题模型来计算每篇新闻的主题分布,作为附加特征与人工特征一起组成新特征集合。
3.1.2 新闻聚类
文档的主题分布可看做是包含语义信息的一个降维过程,低维的主题分布特征可以用来对文档进行聚类。
表3中展示了基于主题分布特征进行K-means聚类的部分结果。从表中可以看出,新闻的主题分布可以很好的完成聚类任务,在簇1中显示的是与房子装修相关的新闻,簇2中则是聚集了与股票相关的新闻。每个簇内的新闻都具有很好的语义相关性。
3.1.3 内容丰富度
在一些信息检索的场景中,我们需要度量网页内容的丰富度,丰富度以在一定程度上反映网页的质量。
通过计算网页的主题分布,我们进一步计算该分布的信息熵,作为衡量网页内容丰富度的指标。信息熵越大,表示网页内容越丰富。网页内容丰富度可以作为一维特征引入到更为复杂的网页排序函数中。
3.2 语义匹配
工业界的很多应用都有在语义上衡量文本相似度的需求,我们将这类需求统称为“语义匹配”。根据文本长度的不同,语义匹配可以细分为三类:短文本-短文本语义匹配,短文本-长文本语义匹配和长文本-长文本语义匹配。
基于主题模型的语义匹配通常作为经典文本匹配技术的补充,而不是取代传统的文本匹配技术。
3.2.1 短文本-短文本语义匹配
3.2.1.1 query-query相关度
由于主题模型在短文本上的效果不太理想,在短文本-短文本匹配任务中词向量的应用比主题模型更为普遍。简单的任务可以使用Word2Vec这种浅层的神经网络模型训练出来的词向量。
3.2.2 短文本-长文本语义匹配
3.2.2.1 query-content相关度
例如:在搜索引擎中,计算一个用户查询(query)和一个网页正文(content)的语义相关度
在计算相似度的时候,我们规避对短文本直接进行主题映射,而是根据长文本的主题分布,计算该分布生成短文本的概率,作为它们之间的相似度:![]()
其中,q表示query, c表示content, w表示q中的词, z k z_k zk表示第k个主题。
3.2.2.2 文档关键词抽取
从文档中抽取关键词,常用的方法是利用词的TF和IDF信息,此外,还可利用主题模型,估计一个文档产生单词的概率作为该单词的重要度指标:![]()
其中, d表示文档内容, w表示词, z k z_k zk表示第k个主题。但由于 P ( w ∣ z k ) P(w|z_k) P(w∣zk)常被高频词主导,导致一些语义上重要的低频词难以被选为关键词。 为了解决上述问题,可以利用TWE训练得到主题和单词的向量表示,再使用公式(3)计算每个词与文档主题的相似度作为衡量语义重要度的指标。![]()
其中, v m → \overrightarrow{v_m} vm表示?对应的词向量, z k → \overrightarrow{z_k} zk表示主题 z k z_k zk对应的主题向量,并且词向量和主题向量在处于同一个向量空间中。
3.2.3 长文本-长文本语义匹配
通过使用主题模型,我们可以得到两个长文本的主题分布,再通过计算两个多项分布的距离来衡量它们之间的相似度。衡量多项分布的距离可以利用Hellinger Distance和Jensen-Shannon Divergence (JSD)。
3.2.3.1 用户画像与个性化推荐
在互联网应用中,当我们积累了用户大量的行为信息后,这些行为信息对应的文本内容可以组合成一篇抽象的“文档”,对该“文档”进行主题映射后获得的主题分布可以作为用户画像。
例如在新闻个性化推荐中,我们可以将用户近期阅读的新闻(或新闻标题)合并成一篇长“文档”,并将该“文档” 的主题分布作为表达用户阅读兴趣的用户画像。通过计算每篇实时新闻的主题分布与用户画像之间的海林格距离(Hellinger Distance),可作为向用户推送新闻的选择依据,达到新闻个性化推荐的效果。
例如在小说推荐任务中,推荐算法常用基于特征的矩阵分解(SVDFeature),考虑到每个用户有一些收藏或者下载的小说,我们可以将这些小说对应的主题分布进行聚合,从而得到用户的主题表示,作为描述用户阅读兴趣的用户画像。通过计算每篇小说的主题分布与用户画像之间的JSD距离,可以用来衡量用户对该小说的感兴趣程度。我们将JSD评分作为全局特征加入到SVDFeature中参与训练,对小说进行排序后推荐给用户
基于特征的矩阵分解(SVDFeature)是一个灵活的推荐框架,允许向模型中增加一些全局特征、用户特征以及物品特征,使得模型在推荐上可以取得更好的效果。
3.2.3.2 垂类新闻CTR预估
新闻推荐服务涉及多个垂类新闻方向,如体育、汽车、娱乐等。在这些方向上,我们往往需要做更精细的个性化推荐。为了实现这个目的,我们需要在垂类新闻数据的基础上,训练针对该垂类的主题模型。
对于某个用户而言,我们把该用户历史上点击的新闻拼接成一篇文档,基于垂类主题模型做主题推断,获得文档的主题分布作为该用户的用户画像。
垂类新闻的CTR预估模型利用的特征可以分为三类:
- 新闻-用户相似度特征:指的是利用长文本-长文本语义匹配的方式计算的新闻和用户画像的相似度。
- 新闻主题特征:指的是该新闻的主题分布。
- 常规的统计特征:包括时间,新闻源,点击率等等。
参考教程
- 一文详解LDA主题模型 - 达观数据 - SegmentFault 思否
https://segmentfault.com/a/1190000012215533 - 文本主题模型之LDA(一) LDA基础 - 刘建平Pinard - 博客园
http://www.cnblogs.com/pinard/p/6831308.html - 周志华《Machine Learning》学习笔记(16)–概率图模型 - VAY-长跑 - CSDN博客
https://blog.csdn.net/u011826404/article/details/75090562 - Home · baidu/Familia Wiki
https://github.com/baidu/Familia/wiki