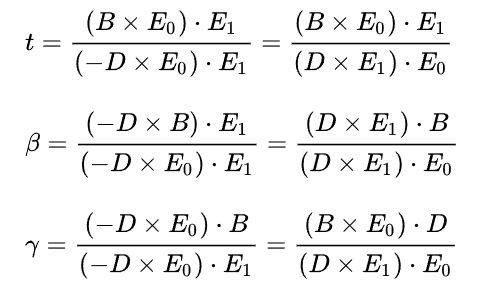光追渲染器开发记录：BVH加速结构构建与射线求交
目录
为什么需要加速：
BVH概念：
BVH的一个节点：
轴对称包围盒AABB：
BVH的构建：
核心思想：
求取最大的包围盒：
BVH求交：
包围盒求交：
基本思想：
平面求交：
具体做法：
具体的物体求交：
三角面求交：
基本思想：
球体求交：
方法一：
方法二：
学习资料：
上一篇：光追渲染器开发记录：基础渲染架构/线程池/泛型单例_This is MX的博客-CSDN博客
https://blog.csdn.net/m0_56399931/article/details/123977009
为什么需要加速：
当我们场景中有大量物体的时候，每根射线都要和每个物体求交的消耗是非常昂贵的，我们需要对求交这个过程进行加速，加速方法通常分为空间划分，物体划分。空间划分有八叉树、KDTree,BSPTree,物体划分有BVH、SAH等。
我们选择最常用的BVH来构建加速结构。
BVH概念：
BVH的一个节点：
BVH主要根据物体的包围盒进行划分，构建二叉树，每个树的节点至少包括左子树指针、右子树指针、包围盒，叶子节点还会包含具体的物体。
轴对称包围盒AABB：
我们的包围盒采用轴对称包围盒，一个轴对称包围盒的定义，可以使用两个vec3，记录最大值Vec_max，最小值Vec_min，然后根据排列组合可以求出包围盒的八个点。
BVH的构建：
我们构建一棵树的时候通常是递归构建的，这里我们也采用递归构建的方法。
核心思想：
①每次我们找出物体列表的最大的包围盒
②然后每次我们找到最长的轴
③根据最长的轴进行排序二分划分，构建左右节点，重复①②③过程
④如果只剩下一个物体则构建叶子节点
⑤如果只剩下两个物体则构建左右叶子节点
求取最大的包围盒：
对于包围盒的列表，更新每个轴的最大最小，然后更新Vec_max（maxX,maxY,maxZ）,更新Vec_min(minX,minY,minZ)
BVH求交：
包围盒求交：
基本思想：
我们先看射线的定义 ray=origin + time *direction 简写为 ray= o +td;
平面的点法表达式子 （arbitrary point- fixed point）· normal=0 ，简写为 （x - p）· n =0，其中x为未知点，p为平面上任意选取的一点，n为法线。
包围盒求交其实就是利用射线与平面的相交，分别求取xyz三个轴的t_min ,t_max，t_min=max(t_min_list)，t_max=min(t_max_list)
我们先看平面求交
平面求交：
其实就是把射线方程带入平面方程
(o+td -p)*n=0
t=(p-o)/d
具体做法：
看到t=(p-o)/d，我们发现这个其实和normal没有关系，那么如果我们选取p为Vec_max，我们就能求取到三个面的射线相交时间，选取p为Vec_min，我们就能求取到另外三个面的射线相交时间。然后我们再取一下min，max，就能获取到射出t，射入t。
具体的物体求交：
三角面求交：
基本思想：
我们先求取射线和平面的交点，然后判断交点是否在三角形内。射线平面求交就是上面的算法，三角形求交，可以采用重心插值公式。
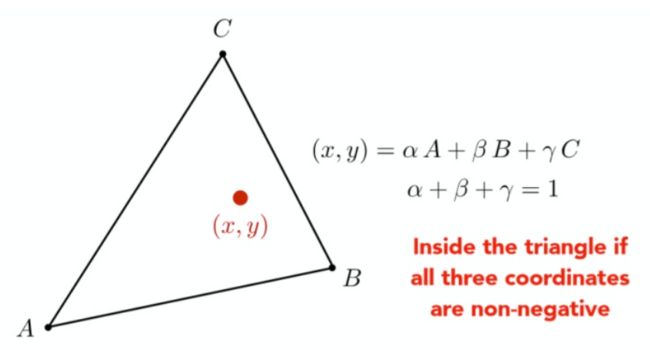
重心插值公式的判断三角形内部点如下
但是我们这么判断其实得计算两个算法，那我们联合一下两个算法求解，这就是Moller-Trumbore算法
我们假设：
根据线性代数只是，可以求出
一个点在三角形内有如下约束
这里粘一下我games作业的代码
球体求交：
球体求交有两个方法，一个是根据方程求解，一个根据数学的射线与球心距离求解
我们这里写一个球体的方程（P-C）^2=R^2，核心思想是球体表面点到圆心的距离永远是半径
方法一：
方程求解：
我们可以将射线方程带入球体方程，观察是否有解，（o+td-c）^2=R^2，展开我们使用判别式判断，如果有交点求出解
方法二：
根据数学的射线与球心距离求解：
我们首先判断射线原点到球心的距离如果小于半径肯定有交点；进一步我们求射线原点到球中心在射线上的投影距离，如果小于0，表明球心在射线原点以及方向背后，没有交点；再进一步，求取球中心到射线的垂直距离平方，如果大于半径肯定没有交点；如果要求t，则再进一步根据勾股定理求取射线与球体两个交点之间的距离，利用投影距离加减算一下就可以求出t。至此求解完成。
学习资料：
Ray Tracing: in One Weekend
Ray Tracing: The Next Week
games101
1.射线与球的相交测试 - 知乎
2.射线与三角形相交 Moller-Trumbore - 知乎
3.【光线追踪系列十】光追加速结构(BVH树)_沉默的舞台剧的博客-CSDN博客_bvh树