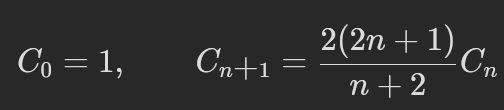力扣刷题记录
开个坑,记录下刷题进度。刚入门小白,仅为记录不供参考
文章目录
- 一、leetcode专项突破:数据结构
-
- 数据结构入门
-
- 217、存在重复元素
-
- F1 暴力法
- F2 先multiset自动排序,再两位的比较
- F3 先sort排序,再两位的比较
- F4 哈希表
- 53、最大子数组和
-
- F1 把每种情况存在map里自动排序
- F2 动态规划
- F3 分治法
- 二、数组和字符串
-
- 1991、找到数组的中间位置
- 三、代码随想录:数组
-
- 1. 二分查找:
- 704. 二分查找(E)
-
- F1 自写,左闭右闭
- F2 左闭右开
- 35.搜索插入位置(E)
-
- F1 二分,左闭右闭
- F2 二分,左闭右开
- 34. 在排序数组中查找元素的第一个和最后一个位置(M)
-
- F1 自写二分,不好
- F2 随想录二分
- F3 官方精简版
- 69.x 的平方根(E)
-
- F1 自写二分
- F2 牛顿法(这个的时间复杂度,回来再看看)
- 官方牛顿法
- 367.有效的完全平方数(E)
-
- F1 自写二分
- 2. 移除元素(双指针法):
- 27. 移除元素(E)
-
- F1 暴力解法
- F2 随想录双指针法
- F3 随想录相向双指针法
- 26.删除排序数组中的重复项(E)
-
- F1 自写双指针
- 283.移动零(E)
-
- F1 自写双指针
- F2 官方双指针,移动0
- 844.比较含退格的字符串(E)
-
- F1 双指针
- F2 栈
- 977.有序数组的平方(E)
-
- F1 暴力法
- F2 双指针
- 3.长度最小的子数组(滑动窗口法)
- 209.长度最小的子数组(M)
-
- F1 暴力解法
- F2 滑动窗口
- 904、水果成篮(M)
-
- F1 滑动窗口
- 76、最小覆盖子串(H)
-
- F1 滑动窗口
- F2、lbld滑动模板(未看
- 螺旋矩阵Ⅱ
- 59.螺旋矩阵II
-
- F1 自写(垃圾
- F2 自写,还不错
- F3 参照随想录
- 54.螺旋矩阵(剑指 Offer 29. 顺时针打印矩阵)
-
- F1 自写
- F2 参考评论,更简洁
- 四、代码随想录:链表
-
- 203、移除链表元素(E)
-
- F1 在原来的链表上进行移除
- F2 设置一个虚拟头结点在进行移除节点操作
- 707、设计链表(M)
-
- F1
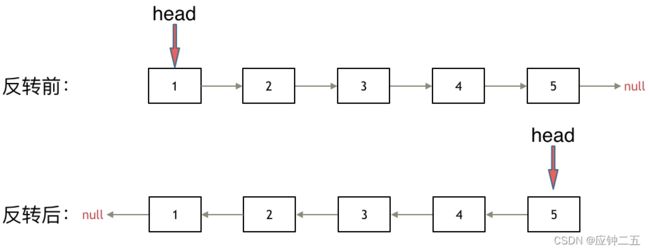
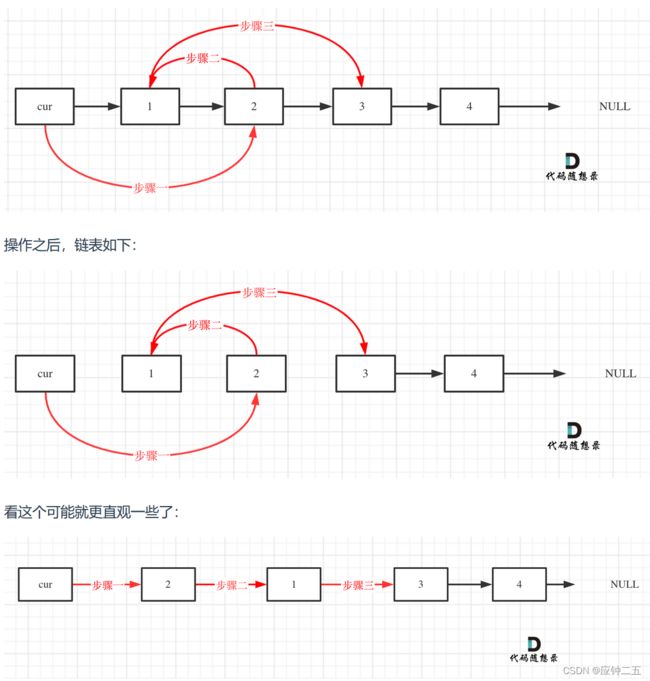
- 206、反转链表
-
- F1 双指针
- F2、递归
- 24. 两两交换链表中的节点(M)
-
- F1
- 19.删除链表的倒数第 N 个结点(M)
-
- F1 不设置虚拟头结点,没写出来
- F2 虚拟头结点
- 面试题 02.07. 链表相交(E)
-
- F1
- 142. 环形链表 II(M)
- 五、代码随想录:哈希表
-
- 242、有效的字母异位词(E)
- 349. 两个数组的交集(E)
- 202. 快乐数(E)
- 1. 两数之和(E)
-
- F1 自写
- F2 参照随想录避免map的key重复的特性
- 454. 四数相加 II(M)
- 383. 赎金信(E)
-
- F1 自写,多循环了一次
- F2 先遍历第二个,就可以少遍历一次vector
- 15. 三数之和(M)
-
- 双指针(最优方法)
- 哈希解法
- 18. 四数之和(M)
-
- 双指针法
- 六、代码随想录:字符串
-
- 344. 反转字符串(E)
-
- F1 自写,没必要用迭代器
- F2
- 541. 反转字符串 II(E)
-
- F1 自写
- F2 随想录,没啥差别
- 剑指 Offer 05. 替换空格(E)
-
- F1 自写,不好
- F2 使用了额外的空间
- F3 扩充原来空间,并用双指针
- 151. 颠倒字符串中的单词
-
- F1 自写
- F2 代码随想录
- F3 随想录版本二
- 剑指 Offer 58 - II. 左旋转字符串(E)
-
- F1
- F2
- F3 随想录
- 28. 实现 strStr()(E)
-
- F1 KMP
- 459.重复的子字符串
-
- F1 枚举
- F2 移动匹配
- F3 KMP
- 七、代码随想录:双指针法
- 八、代码随想录:栈与队列
-
- 232. 用栈实现队列(E)
-
- F1 自写
- F2 随想录
- 其他方法
- 225. 用队列实现栈(E)
-
- F1 双队列实现
- F2 单队列实现
- 20. 有效的括号
-
- F1 自写
- F2 随想录版
- 1047. 删除字符串中的所有相邻重复项
-
- F1 自写
- F2 随想录版
- F3 将字符串直接作为栈
- 150. 逆波兰表达式求值
-
- F1 栈
- 239. 滑动窗口最大值
-
- F1 自写,超时
- F2 优先队列
- F3 单调队列
- 347. 前 K 个高频元素
-
- F1 自写
- F2 随想录,优先级队列
- F3 快速排序(待补充
- 九、代码随想录:二叉树
-
- 94.144.145.二叉树的前中后序遍历
-
- F1 递归
-
- 前
- 中
- 后
- F2 迭代
-
- 前
- 中
- 后
- F3 统一迭代法
-
- 中
- 前
- 后
- 十、代码随想录:回溯算法
-
-
- F1
-
- F1
-
- 十一、代码随想录:贪心算法
-
-
- F1
-
- F1
-
- 十二、代码随想录:动态规划
-
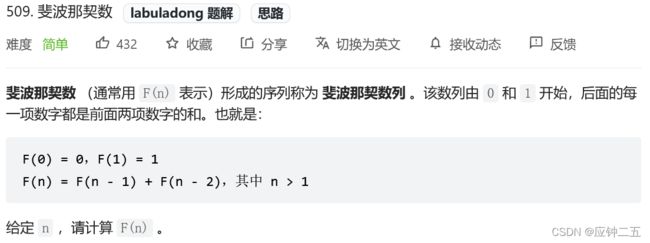
- 509、斐波那契数(E)
-
- F1 暴力递归
- F2 动态规划dp
- F3 精简
- 70、爬楼梯(E)
-
- F1、动态规划
- F2、空间上进行压缩
- 扩展
-
- 自写
- 随想录代码
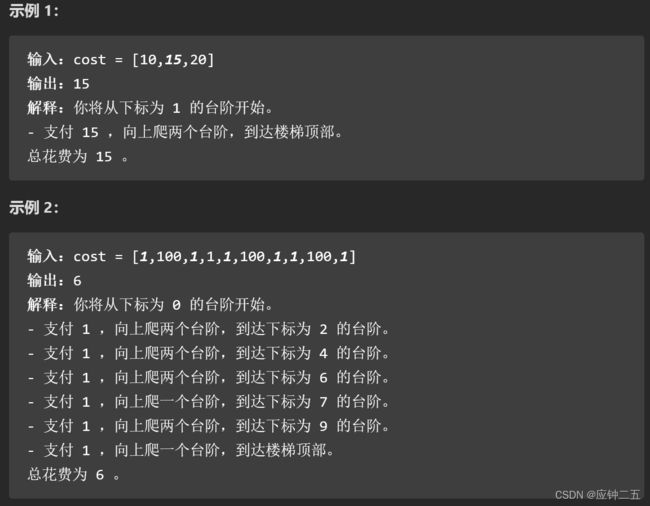
- 746. 使用最小花费爬楼梯(E)
-
- F1 自写
- F2 随想录
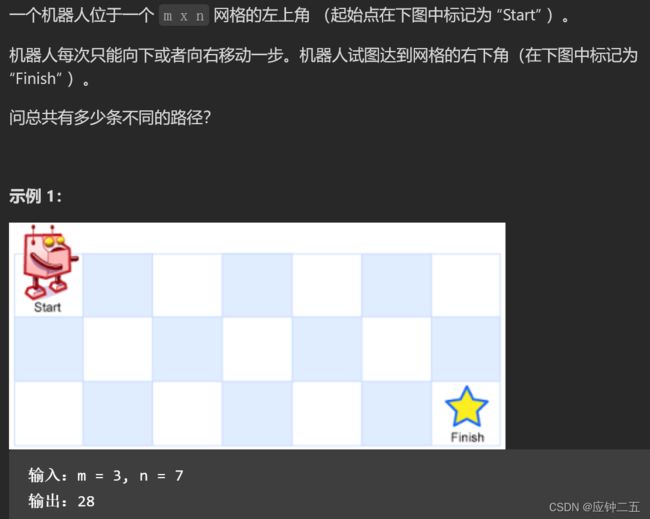
- 62.不同路径(M)
-
- F1 动态规划
- ~~F2 深度搜索,待补充~~
- F3 数论方法
- 63.不同路径II(M)
-
- F1 自写
- F2 随想录简化版
- 343.整数拆分(M) (再看一遍)
-
- F1 数学方法
- F2 动态规划
- F3 贪心算法
- 96.不同的二叉搜索树(M)(再看一遍)
-
- F1 动态规划
- F2 数学(未看)
- 01背包:
-
- 二维dp数组
- 一维dp数组(更常用)
- 416.分割等和子集(M)
-
- F1 自写
- F2 随想录
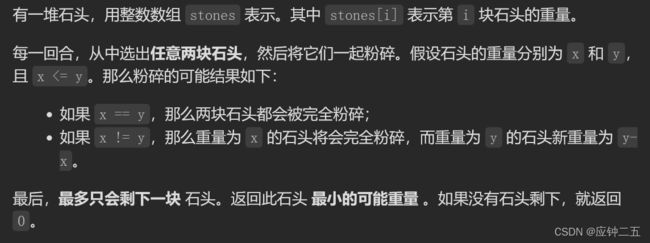
- 1049. 最后一块石头的重量 II(M)
-
- F1 自写动态规划
- 随想录动态规划
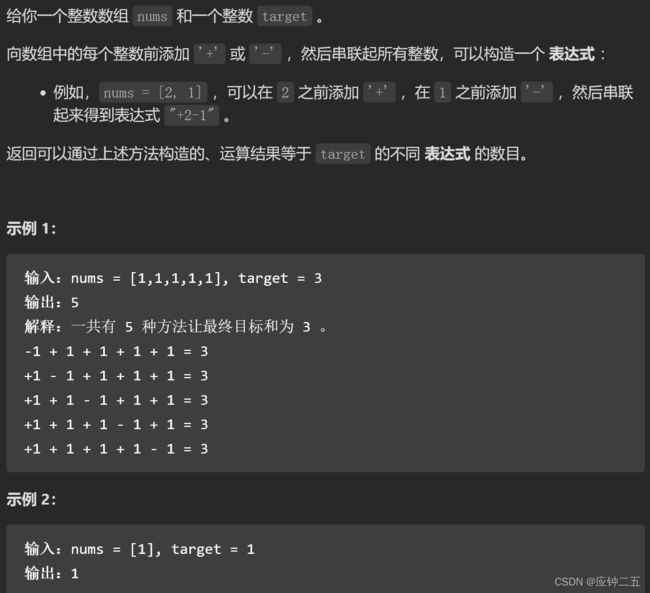
- 494. 目标和(M)
-
- F1 自写
- 随想录
- F2 回溯算法(待补充)
- 474.一和零(M)
-
- F1
- 198、打家劫舍/House Robber(E)
-
- F1 笨蛋规划
- F2 动态规划
- F3 精简
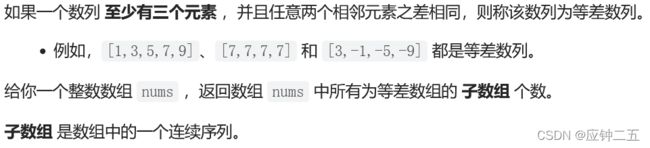
- 413、等差数列划分Arithmetic Slices(M)
-
- F1 自己写的
- F2 标准
- 基本动态规划:二维
-
- 64、最小路径和/Minimum Path Sum(M)
-
- F1、扩充dp并填最大值
- F2、不扩充,靠if增加条件
- F3、再进行空间压缩到一维,自己写的压缩,实际并没有压缩,只是维度变了.....
- F4、真正的空间压缩
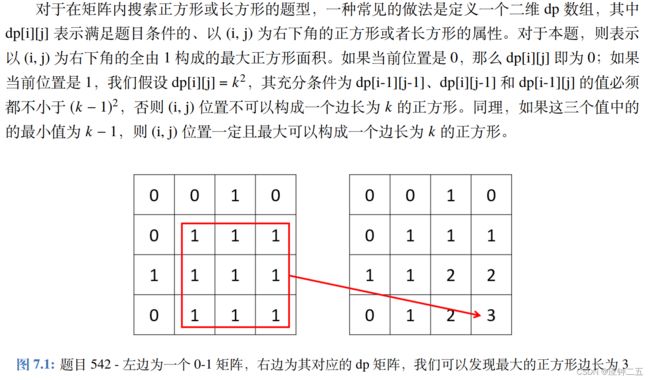
- 542. 01矩阵/01 Matrix (M)
-
- F1、自己写的错误解法
- F2、正确解法
- 221、最大正方形/Maximal Square (Medium)
-
- F1、自写
- F2、答案解法
- 分割类型题
-
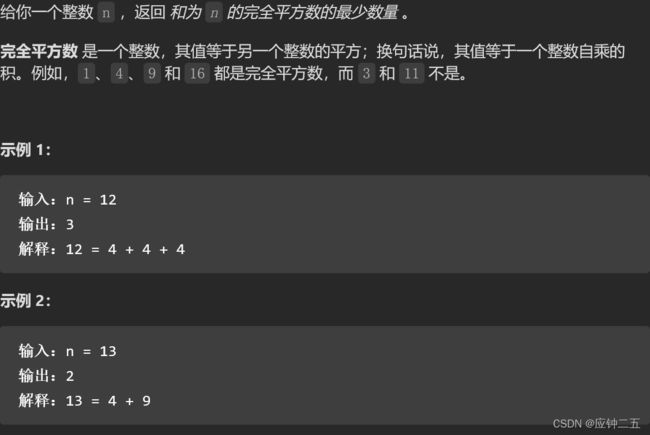
- 279、完全平方数/Perfect Squares (Medium)
-
- F1 动态规划(看答案做的没想出来
- 322、零钱兑换
-
- F1、动态规划
- F2 待补充
一、leetcode专项突破:数据结构
数据结构入门
217、存在重复元素
F1 暴力法
class Solution {
public:
bool containsDuplicate(vector<int>& nums) {
int i,j;
for(i=0;i<sizeof(nums)/sizeof(nums[0])-1;i++){
for(j=i+1;j<sizeof(nums)/sizeof(nums[0]);j++){
if(nums[i]==nums[j]){
return true;
}
}
}
return false;
}
};
问题1,输入[1,2,3,4]时报错
解决:将sizeof(nums)/sizeof(nums[0])换为nums.size()
原因:这个bool函数传入的是vector,而vector计算sizeof的时候是计算vector里面三个指针(first,last,end)的大小,不是vector实际的大小
问题2,超出时间限制
F2 先multiset自动排序,再两位的比较
class Solution {
public:
bool containsDuplicate(vector<int>& nums) {
//通过multiset实现自动排序。用sort也行
multiset<int> st;
for (vector<int>::iterator it = nums.begin(); it != nums.end(); it++)
{
st.insert(*it);
}
for (multiset<int>::iterator iit = st.begin(); iit != st.end()-1; iit++)
{
if(*iit==*(iit+1)){
return true;
}
}
return false;
}
};
问题:排序还不如用sort呢,而且multiset的迭代器不能+1,直接报错
F3 先sort排序,再两位的比较
class Solution {
public:
bool containsDuplicate(vector<int>& nums) {
sort(nums.begin(),nums.end());
for(int i=0;i<nums.size()-1;i++){
if(nums[i]==nums[i+1]){
return true;
}
}
return false;
}
};
执行用时88 ms;内存消耗45.3 MB
问题:用了sort自动排序,不大好
F4 哈希表
哈希表查找的复杂度为O(1)
class Solution {
public:
bool containsDuplicate(vector<int>& nums) {
unordered_set<int> s;
for (int x: nums) {
// 没找到,则s.find(x)返回s.end()
if (s.find(x) != s.end()) {
return true;
}
s.insert(x);
}
return false;
}
};
执行用时76 ms;内存消耗50.1 MB
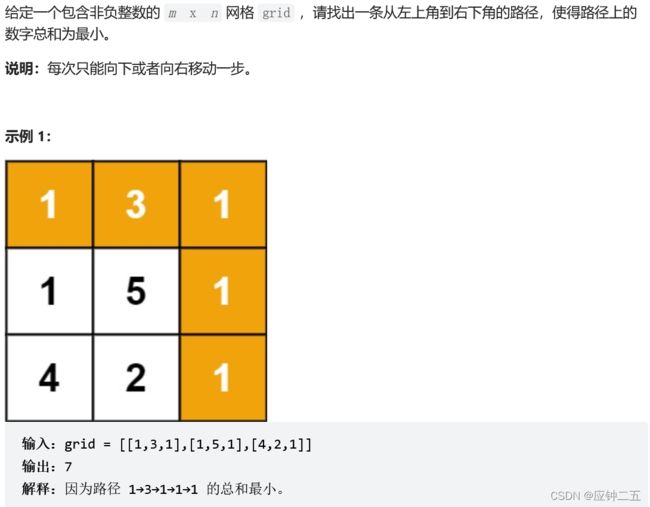
53、最大子数组和
F1 把每种情况存在map里自动排序
class Solution {
public:
int maxSubArray(vector<int>& nums) {
multimap<int, int> m;
int kk;
for(int i=0;i<nums.size();i++){
kk=nums[i];
m.insert(make_pair(nums[i],nums[i]));
for(int j=i+1;j<nums.size();j++){
kk=kk+nums[j];
m.insert(make_pair(kk,kk));
}
}
return (*(--m.end())).first;
}
};
问题1、为什么不加–,m.end()输出是15?是指向的一个不存在的元素,可能随机到了15
问题2、超出时间限制
F2 动态规划
虽然也是拆成多个子问题进行求解,但动态规划保存子问题的解,避免重复计算
在这里插入代码片
F3 分治法
在这里插入代码片
二、数组和字符串
1991、找到数组的中间位置
三、代码随想录:数组
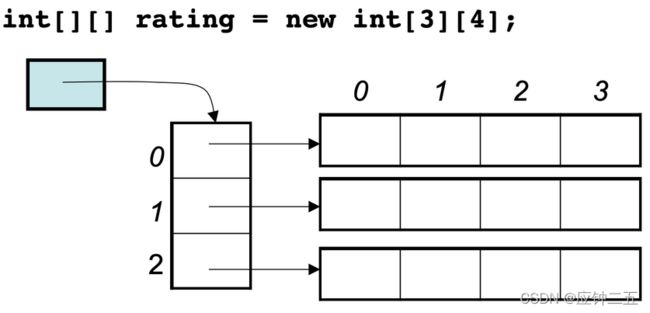
注意,二维数组在内存的空间地址是什么样的?
如: int[][] rating = new int[3][4]; , 这个二维数据在内存空间可不是一个 3*4 的连续地址空间,而是四条连续的地址空间组成
1. 二分查找:
704. 二分查找(E)
F1 自写,左闭右闭
参照算法图解的自写二分
补充:防溢出
mid= low + ((high - low) / 2);;// 防止溢出 等同于(low+ high)/2
class Solution {
public:
int search(vector<int>& nums, int target) {
int mid,high=nums.size()-1,low=0;
while(low<=high){
mid= low + ((high - low) / 2);
if(nums[mid]>target) high=mid-1;
else if(nums[mid]<target) low=mid+1;
else return mid;
};
return -1;
}
};
F2 左闭右开
定义 target 是在一个在左闭右开的区间里,也就是[left, right) 。边界处理不同。
class Solution {
public:
int search(vector<int>& nums, int target) {
int left = 0;
int right = nums.size(); // 定义target在左闭右开的区间里,即:[left, right)
while (left < right) { // 因为left == right的时候,在[left, right)是无效的空间,所以使用 <
int middle = left + ((right - left) >> 1);
if (nums[middle] > target) {
right = middle; // target 在左区间,在[left, middle)中
} else if (nums[middle] < target) {
left = middle + 1; // target 在右区间,在[middle + 1, right)中
} else { // nums[middle] == target
return middle; // 数组中找到目标值,直接返回下标
}
}
// 未找到目标值
return -1;
}
};
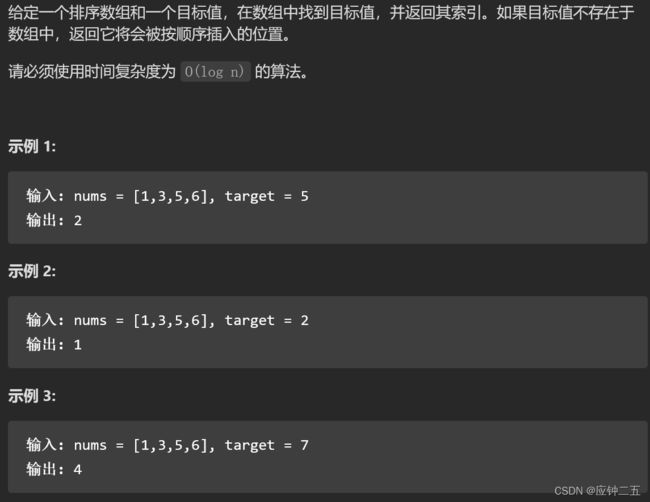
35.搜索插入位置(E)
- 目标值在数组所有元素之前:不断循环后l=m=h=0,return mid
- 目标值等于数组中某一个元素 return mid;
- 目标值插入数组中的位置,return high+ 1
- 目标值在数组所有元素之后的情况 , return high+ 1
F1 二分,左闭右闭
class Solution {
public:
int searchInsert(vector<int>& nums, int target) {
int mid,high=nums.size()-1,low=0;
while(low<=high){
mid= low + ((high - low) / 2);
if(nums[mid]>target) high=mid-1;
else if(nums[mid]<target) low=mid+1;
else return mid;
};
return high+1;// 就修改了这一句
}
};
F2 二分,左闭右开
class Solution {
public:
int searchInsert(vector<int>& nums, int target) {
int mid,high=nums.size(),low=0;
while(low<high){
mid= low + ((high - low) / 2);
if(nums[mid]>target) high=mid;
else if(nums[mid]<target) low=mid+1;
else return mid;
};
return high;
}
};
时间复杂度:O(log n) 空间复杂度:O(1)
34. 在排序数组中查找元素的第一个和最后一个位置(M)
F1 自写二分,不好
思路:
先二分找到位置,用k记录,之后通过while分别向前和向后检索是否相等并记录两个下标
问题:
先二分找到一个target,再寻找左右边界,但找左右边界是一个个找的,比较慢
踩坑:
- 设一个初值-1,k==-1则说明没找到。这里不能用0,因为存在下标为0的情况
- 返回vector用return {-1,-1};大括号的形式
- 两个下标注意考虑最左和最右的边界的情况,并且while中要先判断边界条件,否则下标问题会先报错
class Solution {
public:
vector<int> searchRange(vector<int>& nums, int target) {
int mid,high=nums.size()-1,low=0;
int k=-1;
while(low<=high){
mid= low + ((high - low) / 2);
if(nums[mid]>target) high=mid-1;
else if(nums[mid]<target) low=mid+1;
else{
k=mid;
break;
}
};
if(k==-1){ // 设一个初值-1,k==-1则说明没找到
return {-1,-1};// 返回vector用这个形式
}
else{//注意考虑最左和最右的边界
low=high=k;
// 这里&&优先级更高,所以要加括号;并且要先判断边界条件,否则下标问题会先报错
while((low!=0)&&(nums[low-1]==target)){
low--;}
while((high!=nums.size()-1)&&(nums[high+1]==target)){
high++;}
return {low,high};
}
}
};
F2 随想录二分
计算出来的右边界是不包含target的右边界,左边界同理。最后得到的右边界-1,左边界+1
- 寻找右边界
nums[middle] <= target的情况下,让left往右,rB为left,就能使得最后跳过target,使得r在target上,l和rB在target右边
// 二分查找,寻找target的右边界(不包括target)
// 如果rightBorder为没有被赋值(即target在数组范围的左边,例如数组[3,3],target为2),为了处理情况一
int getRightBorder(vector<int>& nums, int target) {
int left = 0;
int right = nums.size() - 1; // 定义target在左闭右闭的区间里,[left, right]
int rightBorder = -2; // 记录一下rightBorder没有被赋值的情况
while (left <= right) { // 当left==right,区间[left, right]依然有效
int middle = left + ((right - left) / 2);// 防止溢出 等同于(left + right)/2
if (nums[middle] > target) {
right = middle - 1; // target 在左区间,所以[left, middle - 1]
} else { // 当nums[middle] == target的时候,更新left,这样才能得到target的右边界
left = middle + 1;
rightBorder = left;
}
}
return rightBorder;
}
- 寻找左边界
当l和m找到target的时候,nums[middle] == target,right = middle - 1移动到了m左边,同时lB=right,即保存了左边界
// 二分查找,寻找target的左边界leftBorder(不包括target)
// 如果leftBorder没有被赋值(即target在数组范围的右边,例如数组[3,3],target为4),为了处理情况一
int getLeftBorder(vector<int>& nums, int target) {
int left = 0;
int right = nums.size() - 1; // 定义target在左闭右闭的区间里,[left, right]
int leftBorder = -2; // 记录一下leftBorder没有被赋值的情况
while (left <= right) {
int middle = left + ((right - left) / 2);
if (nums[middle] >= target) { // 寻找左边界,就要在nums[middle] == target的时候更新right
right = middle - 1;
leftBorder = right;
} else {
left = middle + 1;
}
}
return leftBorder;
}
- 处理三种情况
- 情况一:target 在数组范围的右边或者左边,例如数组{3, 4, 5},target为2或者数组{3, 4, 5},target为6,此时应该返回{-1, -1}
- 情况二:target 在数组范围中,且数组中不存在target,例如数组{3,6,7},target为5,此时应该返回{-1, -1}
- 情况三:target 在数组范围中,且数组中存在target,例如数组{3,6,7},target为6,此时应该返回{1, 1}
class Solution {
public:
vector<int> searchRange(vector<int>& nums, int target) {
int leftBorder = getLeftBorder(nums, target);
int rightBorder = getRightBorder(nums, target);
// 情况一
if (leftBorder == -2 || rightBorder == -2) return {-1, -1};
// 情况三
if (rightBorder - leftBorder > 1) return {leftBorder + 1, rightBorder - 1};
// 情况二
return {-1, -1};
}
private:
int getRightBorder(vector<int>& nums, int target) {
int left = 0;
int right = nums.size() - 1;
int rightBorder = -2; // 记录一下rightBorder没有被赋值的情况
while (left <= right) {
int middle = left + ((right - left) / 2);
if (nums[middle] > target) {
right = middle - 1;
} else { // 寻找右边界,nums[middle] == target的时候更新left
left = middle + 1;
rightBorder = left;
}
}
return rightBorder;
}
int getLeftBorder(vector<int>& nums, int target) {
int left = 0;
int right = nums.size() - 1;
int leftBorder = -2; // 记录一下leftBorder没有被赋值的情况
while (left <= right) {
int middle = left + ((right - left) / 2);
if (nums[middle] >= target) { // 寻找左边界,nums[middle] == target的时候更新right
right = middle - 1;
leftBorder = right;
} else {
left = middle + 1;
}
}
return leftBorder;
}
};
F3 官方精简版
不易理解
class Solution {
public:
int binarySearch(vector<int>& nums, int target, bool lower) {
int left = 0, right = (int)nums.size() - 1, ans = (int)nums.size();
while (left <= right) {
int mid = (left + right) / 2;
if (nums[mid] > target || (lower && nums[mid] >= target)) {
right = mid - 1;
ans = mid;
} else {
left = mid + 1;
}
}
return ans;
}
vector<int> searchRange(vector<int>& nums, int target) {
int leftIdx = binarySearch(nums, target, true);
int rightIdx = binarySearch(nums, target, false) - 1;
if (leftIdx <= rightIdx && rightIdx < nums.size() && nums[leftIdx] == target && nums[rightIdx] == target) {
return vector<int>{leftIdx, rightIdx};
}
return vector<int>{-1, -1};
}
};
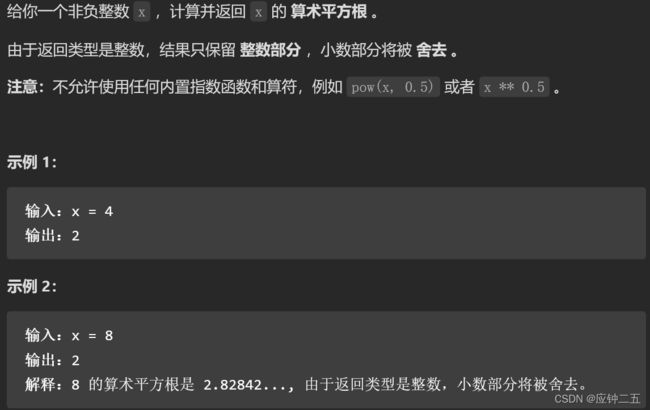
69.x 的平方根(E)
F1 自写二分
class Solution {
public:
int mySqrt(int x) {
if(x==0) return 0;
if(x==1) return 1;
int mid,high=x-1,low=1; // 这里high=x-1可以优化为x/2
while(low<=high){
mid= low + ((high - low) / 2);
if(mid>x/mid) high=mid-1; // 防溢出
else low=mid+1;
};
return low-1;
}
};
F2 牛顿法(这个的时间复杂度,回来再看看)
class Solution {
public:
int s;
int mySqrt(int x) {
if(x==0) return 0;
s=x;
return (int)sqrt(x);
}
double sqrt(double x){
double res=(x+s/x)/2;
if(res==x) return x;
else return sqrt(res);
}
};
官方牛顿法
class Solution {
public:
int mySqrt(int x) {
if (x == 0) {
return 0;
}
double C = x, x0 = x;
while (true) {
double xi = 0.5 * (x0 + C / x0);
if (fabs(x0 - xi) < 1e-7) {
break;
}
x0 = xi;
}
return int(x0);
}
};
时间复杂度:O(logx),此方法是二次收敛的,相较于二分查找更快。
空间复杂度:O(1)
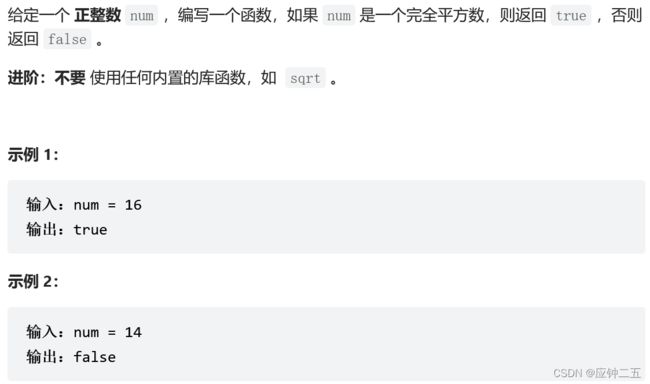
367.有效的完全平方数(E)
F1 自写二分
class Solution {
public:
bool isPerfectSquare(int num) {
int left=1,right=num;
float mid;
while(left<=right){
mid=right+(left-right)/2;
// cout<
float m=(float)num/mid;
if(mid>m) right=(int)mid-1; // 这里用float的类型来判断,避免出现mid=2,5/2=2,导致2=5/2的情况
else if(mid<m) left=(int)mid+1;
else return true;
}
return false;
}
};
2. 移除元素(双指针法):
27. 移除元素(E)
F1 暴力解法
注意,这里比如是1 2 2,i=1的时候检测到相等,移动一轮后,第二个2移动到了i=1的位置,但这时候循环从i=2继续了,因此要i–
class Solution {
public:
int removeElement(vector<int>& nums, int val) {
int count=nums.size();
for(int i=0;i<count;i++){
if(nums[i]==val){
for(int j=i;j<count-1;j++){
nums[j]=nums[j+1];
}
i--;
count--;
}
}
return count;
}
};
时间复杂度:O(n^2)
空间复杂度:O(1)
F2 随想录双指针法
双指针法(快慢指针法): 通过一个快指针和慢指针在一个for循环下完成两个for循环的工作。
class Solution {
public:
int removeElement(vector<int>& nums, int val) {
int slowIndex = 0;
for (int fastIndex = 0; fastIndex < nums.size(); fastIndex++) {
if (val != nums[fastIndex]) nums[slowIndex++] = nums[fastIndex];
}
return slowIndex;
}
};
时间复杂度:O(n),其中n为序列的长度。我们只需要遍历该序列至多两次。
空间复杂度:O(1)
F3 随想录相向双指针法
这是一种优化方法
 这样的方法两个指针在最坏的情况下合起来只遍历了数组一次。与方法一不同的是,方法二避免了需要保留的元素的重复赋值操作。
这样的方法两个指针在最坏的情况下合起来只遍历了数组一次。与方法一不同的是,方法二避免了需要保留的元素的重复赋值操作。
思路:两个指针一个从最左边往右寻找等于val的,一个从最右边往左寻找不等于val的,然后用右边不等于val的赋值过去,再来往左挪动位置
这里可以是while(){},也可以是while(){};,也可以是while() …; 在这里分号和{}的意义都是起一个语句分隔的作用
class Solution {
public:
int removeElement(vector<int>& nums, int val) {
int left = 0, right = nums.size() - 1;
while (left <= right){ // 这里是否需要等于?需要。因为存在l=r的情况,需要对那一位进行判断
// left向右寻找等于val的
while (left <= right && nums[left] != val) left++;
// right向左寻找不为val的,好交换
while (left <= right && nums[right] == val) right--;
// 需要有这个判断才能交换,比如上两部的while存在l==r的情况,这样就不该交换
if (left < right) nums[left++] = nums[right--];
}
// left最后会移动到数组的后一位,刚好为数组大小
return left;
}
};
// 自写的不好的双指针
class Solution {
public:
int removeElement(vector<int>& nums, int val) {
int l = 0;
int r = nums.size() - 1;
for (; l <= r; l++) {
if (nums[l] == val) {
while (r > l && nums[r] == val)
r--;
swap(nums[l],nums[r]);
r--;
}
}
return r+1;
}
};
时间复杂度:O(n),其中n为序列的长度。我们只需要遍历该序列至多一次。
空间复杂度:O(1)
26.删除排序数组中的重复项(E)
F1 自写双指针
从下标为1开始,和前面的一位比较,这样就能保证存入第一个数而不存第二个重复的数
class Solution {
public:
int removeDuplicates(vector<int>& nums) {
if(nums.empty() || nums.size() == 0) return 0;
int j=1;
for (int i = 1; i < nums.size(); i++) { // i为fast
if(nums[i-1]!=nums[i]){
nums[j++]=nums[i];
}
}
return j;
}
};
另一种写法,没啥差别
int removeDuplicates(vector<int>& nums) {
if (nums.size() < 2) return nums.size();
int j = 0;
for (int i = 1; i < nums.size(); i++)
if (nums[j] != nums[i]) nums[++j] = nums[i];
return ++j;
}
283.移动零(E)
F1 自写双指针
思路:先去0,后补0
问题:人家要的是移动0,这写的是删0补0
class Solution {
public:
void moveZeroes(vector<int>& nums) {
int j = 0;
for (int i = 0; i < nums.size(); i++){
if (nums[i] != 0) {
nums[j++] = nums[i];
}
}
for (int i = j; i < nums.size(); i++) {
nums[i] = 0;
}
}
};
F2 官方双指针,移动0
class Solution {
public:
void moveZeroes(vector<int>& nums) {
// 左指针指向当前已经处理好的序列的尾部,右指针指向待处理序列的头部
int left = 0, right = 0;
while (right < nums.size()) {
if (nums[right]) { // 初始时r=l=0。r寻找不为0的
swap(nums[left], nums[right]);
left++; // left指向移动好的序列的末尾,给left换上非0后就移动left
}
right++;
}
}
};
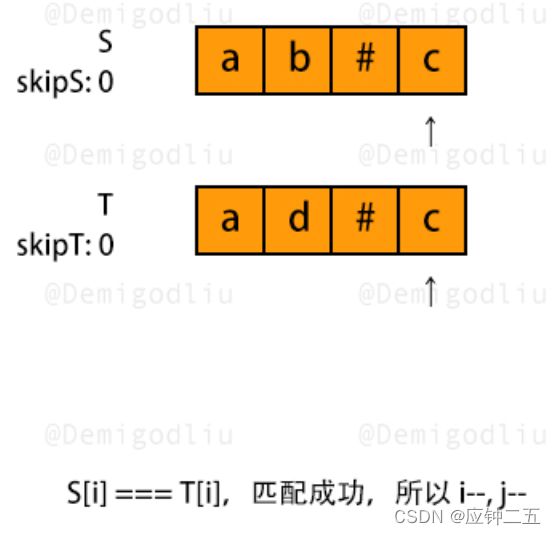
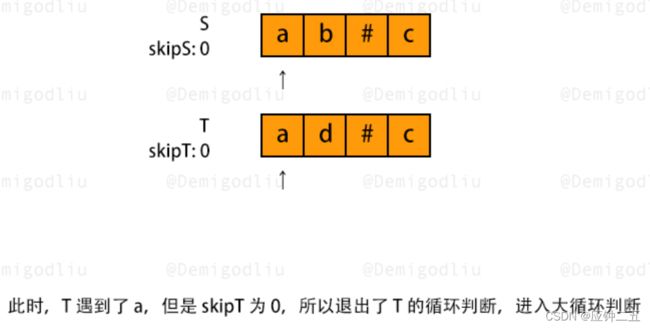
844.比较含退格的字符串(E)
F1 双指针
class Solution {
public:
bool backspaceCompare(string S, string T) {
int i = S.length() - 1, j = T.length() - 1;
int skipS = 0, skipT = 0;
while (i >= 0 || j >= 0) {
// S循环
while (i >= 0) {
if (S[i] == '#') {
skipS++, i--;
} else if (skipS > 0) {
skipS--, i--;
} else {
// skipS变为0时,跳出循环,进行比较
break;
}
}
// T循环
while (j >= 0) {
if (T[j] == '#') {
skipT++, j--;
} else if (skipT > 0) {
skipT--, j--;
} else {
break;
}
}
if (i >= 0 && j >= 0) {
if (S[i] != T[j]) return false;
}
else {
if (i >= 0 || j >= 0) return false;
}
i--, j--;
}
return true;
}
};
F2 栈
这里将string当栈使用,直接用std::basic_string中构造好的函数

class Solution {
public:
bool backspaceCompare(string S, string T) {
return build(S) == build(T);
}
string build(string str) {
string ret;
for (char ch : str) {
if (ch != '#') ret.push_back(ch);
else if (!ret.empty()) ret.pop_back();
}
return ret;
}
};
整合版
class Solution {
public:
bool backspaceCompare(string S, string T) {
string ret1,ret2;
for (char ch : S) {
if (ch != '#') ret1.push_back(ch);
else if (!ret1.empty()) ret1.pop_back();
}
for (char ch : T) {
if (ch != '#') ret2.push_back(ch);
else if (!ret2.empty()) ret2.pop_back();
}
return ret1 == ret2;
}
};
977.有序数组的平方(E)
力扣
F1 暴力法
class Solution {
public:
vector<int> sortedSquares(vector<int>& nums) {
for (int i = 0; i < nums.size(); i++) {
nums[i] = nums[i] * nums[i];
}
sort(nums.begin(), nums.end());
return nums;
}
};
时间:O(nlogn) :sort的时间复杂度为O(nlog2 n),因此具体来讲是O(n + nlogn)
空间:O(logn)。除了存储答案的数组以外,我们需要 O(logn)的栈空间进行排序。
F2 双指针
class Solution {
public:
vector<int> sortedSquares(vector<int>& nums) {
int left = 0, right = nums.size() - 1, pos = right;
vector<int> res(nums.size());
while (pos >= 0) {
if (abs(nums[left]) < abs(nums[right])) {
res[pos] = nums[right] * nums[right];
right--;
}
else {
res[pos] = nums[left] * nums[left];
left++;
}
pos--;
}
return res;
}
};
时间:On
空间:O1:除了存储答案的数组以外,我们只需要维护常量空间
3.长度最小的子数组(滑动窗口法)
209.长度最小的子数组(M)
F1 暴力解法
通过两个循环来找。
class Solution {
public:
int minSubArrayLen(int s, vector<int>& nums) {
int result = INT32_MAX; // 最终的结果,可以直接写INT_MAX
int sum = 0; // 子序列的数值之和
int subLength = 0; // 子序列的长度
for (int i = 0; i < nums.size(); i++) { // 设置子序列起点为i
sum = 0;
for (int j = i; j < nums.size(); j++) { // 设置子序列终止位置为j
sum += nums[j];
if (sum >= s) { // 一旦发现子序列和超过了s,更新result
subLength = j - i + 1; // 取子序列的长度
result = result < subLength ? result : subLength;
break; // 因为我们是找符合条件最短的子序列,所以一旦符合条件就break
}
}
}
// 如果result没有被赋值的话,就返回0,说明没有符合条件的子序列
return result == INT32_MAX ? 0 : result;
}
};
时间复杂度 O(n^2)
空间复杂度 O(1)
F2 滑动窗口
class Solution {
public:
int minSubArrayLen(int s, vector<int>& nums) {
int sum = 0, i = 0, length = INT_MAX; // 滑动窗口数值之和
for (int j = 0; j < nums.size(); j++) {
sum += nums[j];
// 注意这里使用while,每次更新 i(起始位置),并不断比较子序列是否符合条件
while (sum >= s) {
sum = sum - nums[i];
length = (j - i + 1) > length ? length : (j - i + 1);
i++; // 不断变更i(子序列的起始位置)
}
}
return length == INT_MAX ? 0 : length;
}
};
时间复杂度:O(n),虽然for里有一个while,但从每一个元素被操作的次数来看,每个元素在滑动窗后进来操作一次,出去操作一次,每个元素都是被操作两次,所以时间复杂度是 2 × n 也就是O(n)
空间复杂度:O(1)
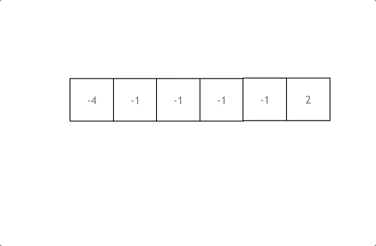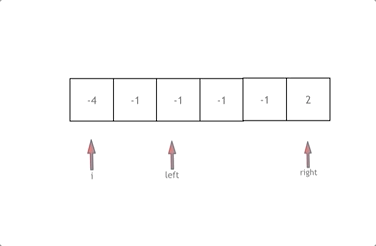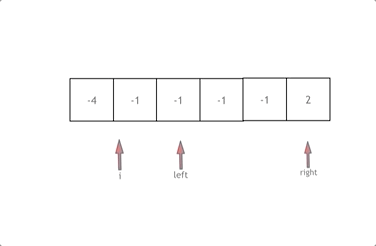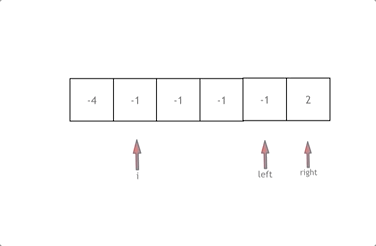
904、水果成篮(M)
F1 滑动窗口
求最多包含k个不同字符的滑动窗口大小
class Solution {
public:
int totalFruit(vector<int>& fruits) {
unordered_map<int, int> window; // 用哈希表的形式,含有带唯一键的键-值对。搜索、插入和元素移除拥有平均常数时间复杂度。
const int k = 2; // 篮子数量
int res = 0;
for (int left = 0, right = 0; right < fruits.size(); right++) {
window[fruits[right]]++; // window[tree[right]]的意思是创建一个key为fruits[right],value为0的对组
while (window.size() > k) {
window[fruits[left]]--;
if (window[fruits[left]] == 0) {
window.erase(fruits[left]);
}
left++;
}
res = max(res, right - left + 1);
}
return res;
}
};
76、最小覆盖子串(H)
力扣
F1 滑动窗口
class Solution {
public:
string minWindow(string s, string t) {
vector<int> need(128,0); // 七位ASCII码用七位2进制表示,可表示128个字符
int count = t.size();
for(char c : t) need[c]++; // 记录需要的每个字符的数量
int l=0, r=0, start=0, size = INT_MAX;
while(r<s.length())
{
char c = s[r];
if(need[c]>0) count--; // 如果c是t中的字符,count--
need[c]--; // 把右边的字符加入窗口
if(count==0) // 窗口中已经包含所需的全部字符
{
while(l<r && need[s[l]]<0) // need[s[l]]<0,即l不在t中,则缩减窗口
{
need[s[l++]]++;
} // 此时窗口符合要求
if(r-l+1 < size) // 窗口缩减完后,更新答案
{
size = r-l+1;
start = l;
}
need[s[l]]++; //左边界右移之前需要释放need[s[l]]
l++;
count++;
}
r++;
}
return size==INT_MAX ? "" : s.substr(start, size); // 返回由start开始的size个字符串
}
};
F2、lbld滑动模板(未看
https://labuladong.github.io/algo/2/18/25/
螺旋矩阵Ⅱ
59.螺旋矩阵II
F1 自写(垃圾
思路:
重复进行右下左上四步操作,每步操作的转折点在到达边缘(第一次循环这四步会出现)和下一个数不为0(不为0意味着已经被赋值)。然后这里因为涉及到了判断下一个数,会出现超出范围的情况,因此在创建数组的时候在左右两边和下边各增加了一行。最后输出的时候再建一个数组,略过这三行进行输出。但这一步相应的时间复杂度会比较高
class Solution {
public:
vector<vector<int>> generateMatrix(int n) {
vector<vector<int>> map(n+1, vector<int>(n + 2, 0));
vector<vector<int>> matrix(n, vector<int>(n, 1));
if (n == 1) return matrix;
int count = 1;
int flag = 1;
int i = 0, j = 1;
while (count <= n * n) {
if (flag == 1) {
map[i][j] = count++;
j++;
if (j == n + 1 || map[i][j] != 0) {
flag = 2;
i++;j--;
if(map[i][j] != 0) break;
}
}
if (flag == 2) {
map[i][j] = count++;
i++;
if (i == n || map[i][j] != 0) {
flag = 3;
j--;i--;
if(map[i][j] != 0) break;
}
}
if (flag == 3) {
map[i][j] = count++;
j--;
if (j == 0 || map[i][j] != 0) {
flag = 4;
i--;j++;
if(map[i][j] != 0) break;
}
}
if (flag == 4) {
map[i][j] = count++;
i--;
if (i == 0 || map[i][j] != 0) {
flag = 1;
j++;i++;
if(map[i][j] != 0) break;
}
}
}
for(int i = 0;i<n;i++){
for(int j = 0;j<n;j++){
matrix[i][j] = map[i][j+1];
}
}
return matrix;
}
};
F2 自写,还不错
对于这种长宽相等的场景,就可以不用去判断边界,用while循环就行
class Solution {
public:
vector<vector<int>> generateMatrix(int n) {
vector<vector<int>> matrix(n, vector<int>(n, 0));
int loop = n - 1; // 每次循环移动数。每圈后减2
int quan = n / 2; // 循环圈数
int mid = n % 2; // 是否会剩一个,比如5对应2圈加最中间那个
int i = 0, j = 0;
int count = 1;
while (quan--) {
int linshi = loop;
while(linshi--) {
matrix[i][j++] = count++;
}
linshi = loop;
while(linshi--) {
matrix[i++][j] = count++;
}
linshi = loop;
while(linshi--) {
matrix[i][j--] = count++;
}
linshi = loop;
while(linshi--) {
matrix[i--][j] = count++;
}
i++;j++;
loop -= 2;
}
if (mid) matrix[n / 2][n / 2] = n * n;
return matrix;
}
};
F3 参照随想录
思路:
可以发现,一共循环n/2圈,按左闭右开的话,第一圈遍历n-1个数,后续每圈遍历n-1 -2个数,然后每圈依次右下左上赋值就行。然后如果是奇数的话,中间会剩一个没遍历到的,需要最后单独赋值。另外每圈的起始位置会变。

class Solution {
public:
vector<vector<int>> generateMatrix(int n) {
vector<vector<int>> map(n, vector<int>(n, 0));
int loop = n / 2;
int x = 0, y = 0; // 定义每个循环的起始位置
int count = 1, q = 0; // q是圈循环后遍历的长度需要减2
int i = 0, j = 0;
while (loop--) {
// 这一步赋初值很重要,之前的报错都是因为忘掉写了
i = x;
j = y;
for (j = y; j < n - 1 - q + y; j++) {
map[i][j] = count++;
}
for (i = x; i < n - 1 - q + x; i++) {
map[i][j] = count++;
}
for (; j > y; j--){
map[i][j] = count++;
}
for (; i > x; i--){
map[i][j] = count++;
}
q += 2;
x++; y++; // 更新起始位置
}
// n % 2 == 1为奇数的话,需要单独给中间位置赋值
if (n % 2) map[n / 2][n / 2] = count;
return map;
}
};
54.螺旋矩阵(剑指 Offer 29. 顺时针打印矩阵)
力扣
F1 自写
仿之前的思路写的,还需要额外考虑特殊情况
class Solution {
public:
vector<int> spiralOrder(vector<vector<int>>& matrix) {
int m = matrix.size(), n = matrix[0].size();
vector<int> map(m * n, 0);
int quan = max(m, n) / 2;
int loop1 = m - 1, loop2 = n - 1;
if(m == 1) {
for(int i = 0; i < n; i++) map[i] = matrix[0][i];
}
else if(n == 1) {
for(int i = 0; i < m; i++) map[i] = matrix[i][0];
}
int i = 0, j = 0;
int count = 0;
while (quan--) {
int linshi = loop2;
while (linshi-- && count<m * n) {
map[count++] = matrix[i][j++];
}
linshi = loop1;
while (linshi-- && count<m * n) {
map[count++] = matrix[i++][j];
}
linshi = loop2;
while (linshi-- && count<m * n) {
map[count++] = matrix[i][j--];
}
linshi = loop1;
while (linshi-- && count<m * n) {
map[count++] = matrix[i--][j];
}
i++;j++;
loop1 -= 2;
loop2 -= 2;
}
if (m == n && n % 2) map[count] = matrix[m / 2][n / 2];
return map;
}
};
F2 参考评论,更简洁
这里的方法不需要记录已经走过的路径,所以执行用时和内存消耗都相对较小
- 首先设定上下左右边界
- 其次向右移动到最右,此时第一行因为已经使用过了,可以将其从图中删去,体现在代码中就是重新定义上边界
- 判断若重新定义后,上下边界交错,表明螺旋矩阵遍历结束,跳出循环,返回答案
- 若上下边界不交错,则遍历还未结束,接着向下向左向上移动,操作过程与第一,二步同理
- 不断循环以上步骤,直到某两条边界交错,跳出循环,返回答案
class Solution {
public:
vector<int> spiralOrder(vector<vector<int>>& matrix) {
vector <int> ans;
if(matrix.empty()) return ans; //若数组为空,直接返回答案
int u = 0; //赋值上下左右边界
int d = matrix.size() - 1;
int l = 0;
int r = matrix[0].size() - 1;
while(true)
{
for(int i = l; i <= r; ++i) ans.push_back(matrix[u][i]); //向右移动直到最右
if(++ u > d) break; //重新设定上边界,若上边界大于下边界,则遍历遍历完成,下同
for(int i = u; i <= d; ++i) ans.push_back(matrix[i][r]); //向下
if(-- r < l) break; //重新设定有边界
for(int i = r; i >= l; --i) ans.push_back(matrix[d][i]); //向左
if(-- d < u) break; //重新设定下边界
for(int i = d; i >= u; --i) ans.push_back(matrix[i][l]); //向上
if(++ l > r) break; //重新设定左边界
}
return ans;
}
};
四、代码随想录:链表
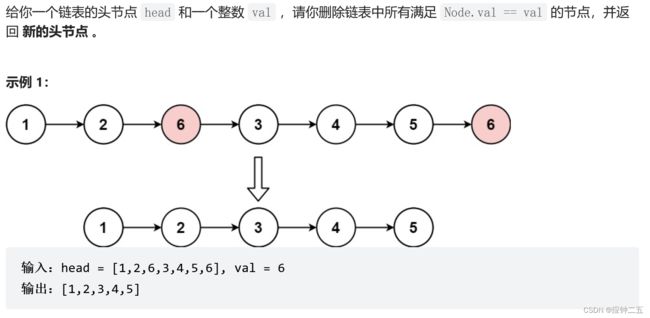
203、移除链表元素(E)
力扣
F1 在原来的链表上进行移除
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* removeElements(ListNode* head, int val) {
// 移除头结点
while(head!=nullptr && head->val == val){
ListNode* tmp = head;
head = head->next;
delete tmp;
}
// 移除非头结点
ListNode* newHead = head;
while(newHead!= nullptr && newHead->next!= nullptr) {
if(newHead->next->val == val) {
ListNode* linshi = newHead->next;
newHead->next = newHead->next->next;
delete linshi;
}
else newHead = newHead->next;
}
return head;
}
};
F2 设置一个虚拟头结点在进行移除节点操作
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* removeElements(ListNode* head, int val) {
ListNode* dummyHead = new ListNode(0,head);
ListNode* newHead = dummyHead;
// 移除非头结点
while(newHead->next!= nullptr) {
if(newHead->next->val == val) {
ListNode* linshi = newHead->next;
newHead->next = newHead->next->next;
delete linshi;
}
else newHead = newHead->next;
}
head = dummyHead->next;
delete dummyHead;
return head;
}
};
707、设计链表(M)
F1
class MyLinkedList {
public:
struct LinkNode{
int val;
LinkNode* next;
LinkNode(int val):val(val),next(nullptr){}
};
// 有虚拟头结点
MyLinkedList() {
node = new LinkNode(0);
size = 0;
}
int get(int index) {
if(index>(size-1) || index<0) return -1;
LinkNode* tmp = node;
index++;//下标从0开始
while(index--){
tmp=tmp->next;
}
return tmp->val;
}
void addAtHead(int val) {
LinkNode* tmp = new LinkNode(val);
tmp->next = node->next;
node->next = tmp;
size++;
}
void addAtTail(int val) {
LinkNode* tmp = new LinkNode(val);
LinkNode* tmp1 = node;
int linshi=size;
while(linshi--){
tmp1=tmp1->next;
}
tmp1->next = tmp;
size++;
}
void addAtIndex(int index, int val) {
if(index>size) return;
LinkNode* tmp1 = new LinkNode(val);
LinkNode* tmp = node;
while(index--){
tmp=tmp->next;
}
tmp1->next = tmp->next;
tmp->next = tmp1;
size++;
}
void deleteAtIndex(int index) {
if (index >= size || index < 0) return;
LinkNode* tmp = node;
while(index--){
tmp = tmp->next;
}
LinkNode* tmp1 = tmp->next;
tmp->next = tmp1->next;
delete tmp1;
size--;
}
// 再写个打印链表
void print(){
LinkNode* tmp = node;
while(tmp->next!=nullptr){
cout<<tmp->next->val<<" ";
tmp=tmp->next;
}
cout<<endl;
}
private:
LinkNode* node;
int size;
};
/**
* Your MyLinkedList object will be instantiated and called as such:
* MyLinkedList* obj = new MyLinkedList();
* int param_1 = obj->get(index);
* obj->addAtHead(val);
* obj->addAtTail(val);
* obj->addAtIndex(index,val);
* obj->deleteAtIndex(index);
*/
206、反转链表
F1 双指针
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* reverseList(ListNode* head) {
ListNode* cur = head;
ListNode* pre = nullptr;
ListNode* tmp;
while (cur) {
tmp = cur->next;//保存一下下一个
cur->next = pre;
pre = cur;
cur = tmp;
}
return pre;
}
};
F2、递归
class Solution {
public:
ListNode* reverse(ListNode* pre,ListNode* cur){
if(cur == nullptr) return pre;
ListNode* tmp = cur->next;
cur->next = pre;
return reverse(cur,tmp);
}
ListNode* reverseList(ListNode* head) {
return reverse(nullptr,head);
}
};
24. 两两交换链表中的节点(M)
F1
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* swapPairs(ListNode* head) {
ListNode* dum = new ListNode(0,head);
ListNode* cur = dum;
ListNode* tmp;
ListNode* tmp1;
while(cur->next!=nullptr && cur->next->next!=nullptr) {
tmp = cur->next;
tmp1 = tmp->next->next;
cur->next = cur->next->next;
cur->next->next = tmp;
tmp->next = tmp1;
cur = cur->next->next;
}
return dum->next;
}
};
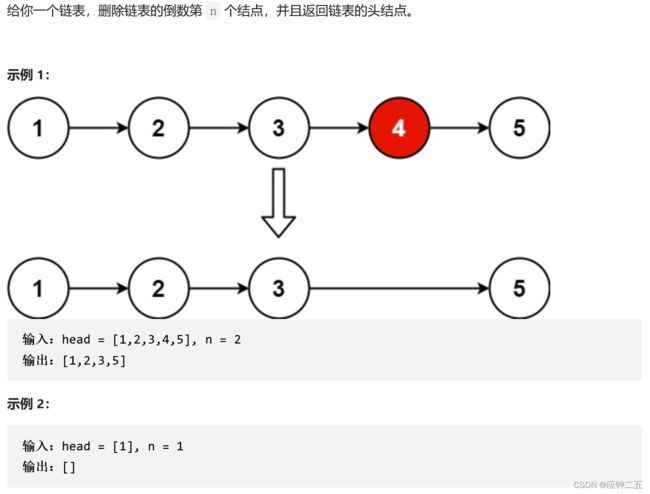
19.删除链表的倒数第 N 个结点(M)
思路:设置快慢指针,快指针先移动n+1次,然后两个指针一起移动,这样就可以刚好快指针指向Null,慢指针指向要删除结点的前一个
F1 不设置虚拟头结点,没写出来
// 不设置虚拟头结点的话,很难处理输入[1],n=1的情况
class Solution {
public:
ListNode* removeNthFromEnd(ListNode* head, int n) {
ListNode *tmp = head;
ListNode *cur = head;
while (n--) {
tmp = tmp->next;
}
while (tmp->next!=nullptr) {
tmp = tmp->next;
cur = cur->next;
}
cur->next = tmp;
return head;
}
};
F2 虚拟头结点
class Solution {
public:
ListNode* removeNthFromEnd(ListNode* head, int n) {
ListNode *dummyHead = new ListNode(0,head);
ListNode *tmp = dummyHead;
ListNode *cur = dummyHead;
while (n--) {
tmp = tmp->next;
}
tmp = tmp->next;
while (tmp!=nullptr) {
tmp = tmp->next;
cur = cur->next;
}
cur->next = cur->next->next;
return dummyHead->next;
}
};
面试题 02.07. 链表相交(E)
力扣
F1
思路:
看如下两个链表,目前curA指向链表A的头结点,curB指向链表B的头结点:
 我们求出两个链表的长度,并求出两个链表长度的差值,然后让curA移动到,和curB 末尾对齐的位置,如图:
我们求出两个链表的长度,并求出两个链表长度的差值,然后让curA移动到,和curB 末尾对齐的位置,如图:
 此时我们就可以比较curA和curB是否相同,如果不相同,同时向后移动curA和curB,如果遇到curA == curB,则找到交点。
此时我们就可以比较curA和curB是否相同,如果不相同,同时向后移动curA和curB,如果遇到curA == curB,则找到交点。
// 思路:链表相交,则从后往前的那一部分是对齐的,因此只需要计算两个链表长度的差值,让长的那个往后移动到短的那个的长度,然后一个个对比就行
class Solution {
public:
ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
int sizeA = 0, sizeB = 0;
ListNode *temp1 = headA, *temp2 = headB;
while (temp1) {
sizeA++;
temp1 = temp1->next;
}
while (temp2) {
sizeB++;
temp2 = temp2->next;
}
temp1 = headA; // 更新到初值,必须先更新后交换
temp2 = headB;
if (sizeA<sizeB) { // 保证长的是A
swap(temp1,temp2);
swap(sizeA,sizeB);
}
int tmp = sizeA - sizeB;
while (tmp--) { // --的左值必须是变量,因此直接(sizeA - sizeB)--是错误的
temp1 = temp1->next;
}
while (temp1 != nullptr) {
if (temp1 == temp2) return temp1;
temp1 = temp1->next;
temp2 = temp2->next;
}
return NULL;
}
};
142. 环形链表 II(M)
力扣
思路
class Solution {
public:
ListNode *detectCycle(ListNode *head) {
ListNode *fast = head;
ListNode *slow = head;
while (fast != nullptr && fast->next != nullptr) {
fast = fast -> next -> next;
slow = slow -> next;
if (fast == slow) {
// 找到了第一次相遇的交点
// 这里可以创建两个新指针分别指向head和交点,这里就直接用fast和slow了,但要注意他们的含义已经变了
fast = head;
while (fast != slow) {
fast = fast -> next;
slow = slow -> next;
}
return fast;
}
}
return NULL;
}
};
五、代码随想录:哈希表
242、有效的字母异位词(E)
力扣
class Solution {
public:
bool isAnagram(string s, string t) {
// 定义在函数体内部的内置类型变量将不被初始化,因此要使用列表初始化为0
int record[26]={};
for(auto ch:s){
record[(int)(ch-'a')]++;
}
for(auto ch:t){
record[(int)(ch-'a')]--;
}
for(int i = 0; i < 26; i++){
if(record[i] != 0) return false;
}
return true;
}
};
349. 两个数组的交集(E)
class Solution {
public:
vector<int> intersection(vector<int>& nums1, vector<int>& nums2) {
unordered_set<int> result;
unordered_set<int> s(nums1.begin(),nums1.end());
for (int num : nums2) {
if(s.find(num) != s.end())
result.insert(num);
}
return vector<int>(result.begin(),result.end());
}
};
202. 快乐数(E)
class Solution {
public:
int get_sum(int n){
int sum = 0;
while(n) {
sum += (n%10)*(n%10);
n = n / 10;
}
return sum;
}
bool isHappy(int n) {
unordered_set<int> s;
int sum = get_sum(n);
while (s.find(sum) == s.end()) {
s.insert(sum);
sum = get_sum(sum);
if (sum == 1) return true;
}
return false;
}
};
1. 两数之和(E)
F1 自写
问题:这里unordered_map的key不能重复,无法处理[3,3]的情况
class Solution {
public:
vector<int> twoSum(vector<int>& nums, int target) {
// 思路:检索比target小的数放到哈希表里
// 依次减每个数,然后在哈希表里找差
// 问题:这里unordered_map的key不能重复,无法处理[3,3]的情况
unordered_map<int,int> s;
vector<int> v;
int count = 0;
for (int num : nums) {
if (num <= target) s.insert(make_pair(num,count));
count++;
}
for (unordered_map<int, int>::iterator it = s.begin(); it != s.end(); it++) {
if(s.find(target - it->first) != s.end()) {
v.push_back(it->second);
v.push_back(s.find(target - it->first)-> second);
return v;
}
}
return {};
// return vector{};
}
};
F2 参照随想录避免map的key重复的特性
class Solution {
public:
vector<int> twoSum(vector<int>& nums, int target) {
unordered_map<int,int> s;
for (int i = 0; i < nums.size(); i++) {
if(s.find(target - nums[i]) != s.end()) {
return {s.find(target - nums[i])->second, i};
}
s.insert(make_pair(nums[i], i));
}
return {};
}
};
454. 四数相加 II(M)
力扣
思路:
- 首先定义 一个unordered_map,key放a和b两数之和,value 放a和b两数之和出现的次数。
- 遍历大A和大B数组,统计两个数组元素之和,和出现的次数,放到map中。
- 定义int变量count,用来统计 a+b+c+d = 0 出现的次数。
- 在遍历大C和大D数组,找到如果 0-(c+d) 在map中出现过的话,就用count把map中key对应的value也就是出现次数统计出来。
- 最后返回统计值 count 就可以了
class Solution {
public:
int fourSumCount(vector<int>& nums1, vector<int>& nums2, vector<int>& nums3, vector<int>& nums4) {
unordered_map<int,int> ab; // key放a和b两数之和,value 放a和b两数之和出现的次数
int count = 0;
for (auto num1 : nums1) {
for (auto num2 : nums2) {
// 可以简化为ab[num1+num2]++;会自动创建出一个key为num1+num2,value为0的pair
if(ab.find(num1+num2)!=ab.end()) ab[num1+num2]++;
else ab[num1+num2] = 1;
}
}
// 遍历大C和大D数组,找到如果 0-(c+d) 在map中出现过的话,就用count把map中key对应的value也就是出现次数统计出来。
for (auto num1 : nums3) {
for (auto num2 : nums4) {
if(ab.find(-(num1+num2))!=ab.end()) count += ab[-(num1+num2)];
}
}
return count;
}
};
383. 赎金信(E)
F1 自写,多循环了一次
class Solution {
public:
bool canConstruct(string ransomNote, string magazine) {
// 先数组统计一下
vector<int> v(26,0);
for (auto s : ransomNote) v[s-'a']++;
for (auto s : magazine) v[s-'a']--;
for (auto i : v) if (i > 0) return false;
return true;
}
};
F2 先遍历第二个,就可以少遍历一次vector
class Solution {
public:
bool canConstruct(string ransomNote, string magazine) {
vector<int> v(26,0);
for (auto s : magazine) v[s-'a']++;
for (auto s : ransomNote) {
v[s-'a']--;
if (v[s-'a'] < 0) return false;
}
return true;
}
};
15. 三数之和(M)
双指针(最优方法)
拿这个nums数组来举例,首先将数组排序,然后有一层for循环,i从下标0的地方开始,同时定一个下标left 定义在i+1的位置上,定义下标right 在数组结尾的位置上。
依然还是在数组中找到 abc 使得a + b +c =0,我们这里相当于 a = nums[i] b = nums[left] c = nums[right]。
接下来如何移动left 和right呢, 如果nums[i] + nums[left] + nums[right] > 0 就说明 此时三数之和大了,因为数组是排序后了,所以right下标就应该向左移动,这样才能让三数之和小一些。
如果 nums[i] + nums[left] + nums[right] < 0 说明 此时 三数之和小了,left 就向右移动,才能让三数之和大一些,直到left与right相遇为止。
class Solution {
public:
vector<vector<int>> threeSum(vector<int>& nums) {
vector<vector<int>> result;
// 先进行排序
sort(nums.begin(), nums.end());
// 找出a + b + c = 0
// a = nums[i], b = nums[left], c = nums[right]
for (int i = 0; i < nums.size(); i++) {
// 排序之后如果第一个元素已经大于零,那么无论如何组合都不可能凑成三元组,直接返回结果就可以了
if (nums[i] > 0) {
return result;
}
// 错误去重方法,将会漏掉-1,-1,2 这种情况
/*
if (nums[i] == nums[i + 1]) {
continue;
}
*/
// 正确去重方法,这样先检索完前面的-1有无三元组后,再检索第二个-1时,才应该发现是重复,然后跳过此次循环
if (i > 0 && nums[i] == nums[i - 1]) {
continue;
}
int left = i + 1;
int right = nums.size() - 1;
while (right > left) {
// 去重复逻辑如果放在这里,0,0,0 的情况,可能直接导致 right<=left 了,从而漏掉了 0,0,0 这种三元组
/*
while (right > left && nums[right] == nums[right - 1]) right--;
while (right > left && nums[left] == nums[left + 1]) left++;
*/
if (nums[i] + nums[left] + nums[right] > 0) {
right--;
// 当前元素不合适了,可以去重,这里的去重即right右移了一位后还是相同的值
while (left < right && nums[right] == nums[right + 1]) right--;
}
else if (nums[i] + nums[left] + nums[right] < 0) {
left++;
// 不合适,去重
while (left < right && nums[left] == nums[left - 1]) left++;
}
else {
result.push_back(vector<int>{nums[i], nums[left], nums[right]});
// 去重逻辑应该放在找到一个三元组之后
while (right > left && nums[right] == nums[right - 1]) right--;
while (right > left && nums[left] == nums[left + 1]) left++;
// 找到答案时,双指针同时收缩,这样才能保证同时增大和减小,才有可能保持三元组
right--;
left++;
}
}
}
return result;
}
};
哈希解法
两层for循环就可以确定 a 和b 的数值了,可以使用哈希法来确定 0-(a+b) 是否在 数组里出现过,其实这个思路是正确的,但是我们有一个非常棘手的问题,就是题目中说的不可以包含重复的三元组。
把符合条件的三元组放进vector中,然后再去重,这样是非常费时的,很容易超时,也是这道题目通过率如此之低的根源所在。
去重的过程不好处理,有很多小细节,如果在面试中很难想到位。
时间复杂度可以做到 O ( n 2 ) O(n^2) O(n2),但还是比较费时的,因为不好做剪枝操作。
class Solution {
public:
vector<vector<int>> threeSum(vector<int>& nums) {
vector<vector<int>> result;
sort(nums.begin(), nums.end());
// 找出a + b + c = 0
// a = nums[i], b = nums[j], c = -(a + b)
for (int i = 0; i < nums.size(); i++) {
// 排序之后如果第一个元素已经大于零,那么不可能凑成三元组
if (nums[i] > 0) {
break;
}
if (i > 0 && nums[i] == nums[i - 1]) { //三元组元素a去重
continue;
}
unordered_set<int> set;
for (int j = i + 1; j < nums.size(); j++) {
if (j > i + 2
&& nums[j] == nums[j-1]
&& nums[j-1] == nums[j-2]) { // 三元组元素b去重
continue;
}
int c = 0 - (nums[i] + nums[j]);
if (set.find(c) != set.end()) {
result.push_back({nums[i], nums[j], c});
set.erase(c);// 三元组元素c去重
} else {
set.insert(nums[j]);
}
}
}
return result;
}
};
18. 四数之和(M)
双指针法
四数之和的双指针解法是两层for循环nums[k] + nums[i]为确定值,依然是循环内有left和right下标作为双指针,找出nums[k] + nums[i] + nums[left] + nums[right] == target的情况,三数之和的时间复杂度是 O ( n 2 ) O(n^2) O(n2),四数之和的时间复杂度是 O ( n 3 ) O(n^3) O(n3) 。
class Solution {
public:
vector<vector<int>> fourSum(vector<int>& nums, int target) {
// 思路1,类似四数相加二,将a+b放入unordered_map中,key为a+b,value为[a,b]的vector;再检索t-(a+b),检索到就将a+b和t-(a+b)的value组合后输出
// 问题:可能很多a+b得到的key是重复的,unordered_map不可重复,所以此方法不可行
// 思路2,类似三数之和
vector<vector<int>> result;
// 先进行排序
sort(nums.begin(), nums.end());
for (int z = 0; z < nums.size(); z++) {
// 这种剪枝是错误的,因为target是任意的,比如为-3,排序后列表为[-2,-1],此时尽管nums[z] > target,但两数相加仍为target
// if (nums[z] > target) {
// return result;
// }
// 这里的去重还是要有的,比如[-2,-2,-1],target为-3,若是不去重,会有两个-2.-1
if (z > 0 && nums[z] == nums[z - 1]) {
continue;
}
for (int i = z + 1; i < nums.size(); i++) {
// 这里也要有个去重,避免-2,-2,-2,-1这种三连重复的情况。因为这是四元组,所以类似的去重还需要有一次
if (i > z + 1 && nums[i] == nums[i - 1]) {
continue;
}
int left = i + 1;
int right = nums.size() - 1;
while (right > left) {
// 这里也要注意,nums[z] + nums[i] + nums[left] + nums[right] > target 会溢出,应该是因为负值
if (nums[z] + nums[i] > target - (nums[left] + nums[right])) {
right--;
// 当前元素不合适了,可以去重
while (left < right && nums[right] == nums[right + 1]) right--;
}
else if (nums[z] + nums[i] < target - (nums[left] + nums[right])) {
left++;
// 不合适,去重
while (left < right && nums[left] == nums[left - 1]) left++;
}
else {
result.push_back(vector<int>{nums[z], nums[i], nums[left], nums[right]});
// 去重逻辑应该放在找到一个四元组之后
while (right > left && nums[right] == nums[right - 1]) right--;
while (right > left && nums[left] == nums[left + 1]) left++;
// 找到答案时,双指针同时收缩,这样才能保证同时增大和减小,才有可能保持四元组
right--;
left++;
}
}
}
}
return result;
}
};
六、代码随想录:字符串
344. 反转字符串(E)
力扣
F1 自写,没必要用迭代器
class Solution {
public:
void reverseString(vector<char>& s) {
// 从两边到中间,两两交换
auto sStart = s.begin();
auto sEnd = --s.end();
while(sStart != sEnd && sEnd > sStart) {
char tmp;
tmp = *sStart;
*sStart = *sEnd;
*sEnd = tmp;
sStart++;
sEnd--;
}
return;
}
};
F2
class Solution {
public:
void reverseString(vector<char>& s) {
// 从两边到中间,两两交换
for (int i = 0, j = s.size() - 1; i <= j; i++, j--) {
// 或直接swap(s[i],s[j]);
char tmp = s[i];
s[i] = s[j];
s[j] = tmp;
}
}
};
541. 反转字符串 II(E)
力扣
F1 自写
class Solution {
public:
string reverseStr(string s, int k) {
for (int i = 0, j = i + k - 1; i < s.size() - 1; i += 2*k, j += 2*k) {
if ((i + k) > s.size() - 1) {
reverse(s.begin() + i, s.end());
return s;
}
reverse(s.begin() + i, s.begin() + i + k);
}
return s;
}
};
F2 随想录,没啥差别
class Solution {
public:
string reverseStr(string s, int k) {
for (int i = 0; i < s.size(); i += (2 * k)) {
// 1. 每隔 2k 个字符的前 k 个字符进行反转
// 2. 剩余字符小于 2k 但大于或等于 k 个,则反转前 k 个字符
if (i + k <= s.size()) {
reverse(s.begin() + i, s.begin() + i + k );
continue;
}
// 3. 剩余字符少于 k 个,则将剩余字符全部反转。
reverse(s.begin() + i, s.begin() + s.size());
}
return s;
}
};
剑指 Offer 05. 替换空格(E)
力扣
F1 自写,不好
遍历一遍s,得到空格位置,再遍历一遍v,替换s中相应位置。问题不在于replace时间复杂度为O(n),而是这直接用了替换的函数,不大好
class Solution {
public:
string replaceSpace(string s) {
int count = 0;
vector<int> v;
for (auto i : s) {
if (i == ' ') {
v.push_back(count);
}
count++;
}
for (int i = 0; i < v.size(); i++) {
s.replace(v[i] + i * 2, 1, "%20");
}
return s;
}
};
F2 使用了额外的空间
class Solution {
public:
string replaceSpace(string s) {
string result;
for (auto i : s) {
if (i == ' ') {
result.append("%20");
}
else{
result.push_back(i);
}
}
return result;
}
};
F3 扩充原来空间,并用双指针
随想录方法,时间复杂度O(n),空间复杂度O(1)
class Solution {
public:
string replaceSpace(string s) {
int count = 0;
int a = s.size();
for (auto i : s) {
if (i == ' ') count++;
}
s.resize(a + count * 2);
int i = a - 1, j = s.size() - 1;
while (i >= 0) {
if(s[i] == ' ') {
s[j--] = '0';
s[j--] = '2';
s[j--] = '%';
i--;
}
else{
s[j--] = s[i--];
}
}
return s;
}
};
151. 颠倒字符串中的单词
力扣
F1 自写
思路:双指针,m指向单词的末尾,n指向单词的最开头
不好,缝缝补补
class Solution {
public:
string reverseWords(string s) {
string result;
int m = s.size() - 1;
int n;
if(m == 0) {
result.push_back(s[0]);
return result;
}
while(1) {
// 令m停在单词的最后一个位置
while(m!=0 && s[m]==' ') {
m--;
}
if(m==0 && s[m]==' ') {
if(result.back() == ' ') result.pop_back();
return result;
}
if(m==0) n = m;
else n = m - 1;
if(s[n] == ' ') n = m;
else{
while (n!=0 && s[n - 1] != ' ') {
n--;
}
}
result.append(s, n, m - n + 1);
result.push_back(' ');
if(n==0) {
if(result.back() == ' ') result.pop_back();
return result;
}
m = n - 1;
}
return result;
}
};
F2 代码随想录
不使用辅助空间,空间复杂度要求为O(1)。
解题思路如下:
移除多余空格
将整个字符串反转
将每个单词反转
举个例子,源字符串为:"the sky is blue "
移除多余空格 : "the sky is blue"
字符串反转:"eulb si yks eht"
单词反转:"blue is sky the"
// 版本一
class Solution {
public:
// 反转字符串s中左闭又闭的区间[start, end]
void reverse(string& s, int start, int end) {
for (int i = start, j = end; i < j; i++, j--) {
swap(s[i], s[j]);
}
}
// 移除冗余空格:使用双指针(快慢指针法)O(n)的算法
// 若嵌套使用erase,则时间复杂度为O(n^2),因为erase的时间复杂度为O(n)
void removeExtraSpaces(string& s) {
int slowIndex = 0, fastIndex = 0; // 定义快指针,慢指针
// 去掉字符串前面的空格
while (s.size() > 0 && fastIndex < s.size() && s[fastIndex] == ' ') {
fastIndex++;
}
for (; fastIndex < s.size(); fastIndex++) {
// 去掉字符串中间部分的冗余空格
if (fastIndex - 1 > 0
&& s[fastIndex - 1] == s[fastIndex]
&& s[fastIndex] == ' ') {
continue;
} else {
s[slowIndex++] = s[fastIndex];
}
}
if (slowIndex - 1 > 0 && s[slowIndex - 1] == ' ') { // 去掉字符串末尾的空格
s.resize(slowIndex - 1);
} else {
s.resize(slowIndex); // 重新设置字符串大小
}
}
/* 主函数简单写法
string reverseWords(string s) {
removeExtraSpaces(s);
reverse(s, 0, s.size() - 1);
for(int i = 0; i < s.size(); i++) {
int j = i;
// 查找单词间的空格,翻转单词
while(j < s.size() && s[j] != ' ') j++;
reverse(s, i, j - 1);
i = j;
}
return s;
}
*/
string reverseWords(string s) {
removeExtraSpaces(s); // 去掉冗余空格
reverse(s, 0, s.size() - 1); // 将字符串全部反转
int start = 0; // 反转的单词在字符串里起始位置
int end = 0; // 反转的单词在字符串里终止位置
bool entry = false; // 标记枚举字符串的过程中是否已经进入了单词区间
for (int i = 0; i < s.size(); i++) { // 开始反转单词
if (!entry) {
start = i; // 确定单词起始位置
entry = true; // 进入单词区间
}
// 单词后面有空格的情况,空格就是分词符
if (entry && s[i] == ' ' && s[i - 1] != ' ') {
end = i - 1; // 确定单词终止位置
entry = false; // 结束单词区间
reverse(s, start, end);
}
// 最后一个结尾单词之后没有空格的情况
if (entry && (i == (s.size() - 1)) && s[i] != ' ' ) {
end = i;// 确定单词终止位置
entry = false; // 结束单词区间
reverse(s, start, end);
}
}
return s;
}
};
F3 随想录版本二
思路同版本一,但更简洁
//版本二:
//原理同版本1,更简洁实现。
class Solution {
public:
void reverse(string& s, int start, int end){ //翻转,区间写法:闭区间 []
for (int i = start, j = end; i < j; i++, j--) {
swap(s[i], s[j]);
}
}
void removeExtraSpaces(string& s) {//去除所有空格并在相邻单词之间添加空格, 快慢指针。
int slow = 0; //整体思想参考Leetcode: 27. 移除元素:https://leetcode-cn.com/problems/remove-element/
for (int i = 0; i < s.size(); ++i) { //
if (s[i] != ' ') { //遇到非空格就处理,即删除所有空格。
if (slow != 0) s[slow++] = ' '; //手动控制空格,给单词之间添加空格。slow != 0说明不是第一个单词,需要在单词前添加空格。
while (i < s.size() && s[i] != ' ') { //补上该单词,遇到空格说明单词结束。
s[slow++] = s[i++];
}
}
}
s.resize(slow); //slow的大小即为去除多余空格后的大小。
}
string reverseWords(string s) {
removeExtraSpaces(s); //去除多余空格,保证单词之间之只有一个空格,且字符串首尾没空格。
reverse(s, 0, s.size() - 1);
int start = 0; //removeExtraSpaces后保证第一个单词的开始下标一定是0。
for (int i = 0; i <= s.size(); ++i) {
if (i == s.size() || s[i] == ' ') { //到达空格或者串尾,说明一个单词结束。进行翻转。
reverse(s, start, i - 1); //翻转,注意是左闭右闭 []的翻转。
start = i + 1; //更新下一个单词的开始下标start
}
}
return s;
}
};
剑指 Offer 58 - II. 左旋转字符串(E)
力扣
F1
自写,将前n个字符添加到s后, 再擦除前n个
class Solution {
public:
string reverseLeftWords(string s, int n) {
// 思路1
for(int i = 0; i < n; i++) {
s.push_back(s[i]);
}
s.erase(0, n);
return s;
}
};
F2
将s的长度扩大一倍,再截取从n开始的size段
空间复杂度为O(n)
class Solution {
public:
string reverseLeftWords(string s, int n) {
s += s;
// 这里s.size()扩大了两倍,因此是s.size()/2
return s.substr(n,s.size()/2);
}
};
F3 随想录
class Solution {
public:
string reverseLeftWords(string s, int n) {
// 不申请空间,只在本串上操作
reverse(s.begin(), s.begin() + n);
reverse(s.begin() + n, s.end());
reverse(s.begin(), s.end());
return s;
}
};
28. 实现 strStr()(E)
力扣
KMP主要应用在字符串匹配上。KMP的主要思想是当出现字符串不匹配时,可以知道一部分之前已经匹配的文本内容,可以利用这些信息避免从头再去做匹配了。
时间复杂度为匹配过程的O(n)与next数组生成的O(m)之和,即O(m+n),而暴力解法为O(m*n),其中haystack为文本串,长度为n, needle为模式串,长度为m。
F1 KMP
这里的next数组为前缀表统一减1
class Solution {
public:
// 构造next数组
// 这里string&将string声明为引用可以避免对元素的拷贝
// 常量引用主要用来修饰形参,防止误操作
void getNext(int* next, const string& s) {
// 这里使用了整体减一的next数组
int j = -1;
// 初始化Next数组
next[0] = j;
// 注意,因为是和j+1比,所以i从1开始
for (int i = 1; i < s.size(); i++) {
// 若前后缀不同,j向前回退
while (j >= 0 && s[j+1] != s[i]) {
j = next[j];
}
// 相同前后缀,则j自增
if (s[i] == s[j+1]) j++;
next[i] = j;
}
}
int strStr(string haystack, string needle) {
// 创建一个前缀表,存储每个位置的最长公共前后缀
// 通过前缀表不一样的位置处的前一个位置的值进行跳转
if (needle.size() == 0) {
return 0;
}
int next[needle.size()];
getNext(next, needle);
// 因为next数组里记录的起始位置为-1
int j = -1;
for(int i = 0; i < haystack.size(); i++) {
while(j >= 0 && haystack[i] != needle[j+1]){
j = next[j];
}
// 匹配,j和i同时向后移动
if (haystack[i] == needle[j + 1]) {
j++; // i的增加在for循环里
}
// 文本串haystack里出现了模式串t
if (j == (needle.size() - 1) ) {
return (i - needle.size() + 1);
}
}
return -1;
}
};
459.重复的子字符串
力扣
F1 枚举
class Solution {
public:
bool repeatedSubstringPattern(string s) {
int n = s.size();
// i可以理解为第一个字串的终止位置
// 因为至少有一个字串重复,所以只需要在前半段枚举
for (int i = 1; i * 2 <= n; i++) {
// 比如n=9时,只可能重复3。如果拿i=2比的话,最后会漏一个
if (n % i == 0) {
bool a = true;
// 从下个字串开始和前面的比对
for (int j = i; j < n; j++) {
if (s[j] != s[j - i]) {
a = false;
break;
}
}
if (a)
return true;
}
}
return false;
}
};
F2 移动匹配
// 力扣官方版
class Solution {
public:
bool repeatedSubstringPattern(string s) {
// find(s, 1)表示从位置1开始查找
// find返回s第一次出现的位置,返回的是下标,这里!= s.size(),就相当于
// 如果那个位置是s.size(),则意味着我们查找到的是第二个s
// 让其不等于,就相当于不计入字符串的最后一个位置
return (s + s).find(s, 1) != s.size();
}
};
// 随想录掐头去尾版
class Solution {
public:
bool repeatedSubstringPattern(string s) {
string t = s + s;
// erase的时间复杂度为O(n)
t.erase(t.begin());
t.erase(t.end() - 1);
// npos可以表示string的结束位子,是string::type_size 类型的,也就是find()返回的类型
// find函数在找不到指定值的情况下会返回string::npos。
return t.find(s) != string::npos;
}
};
F3 KMP
时间复杂度:O(n),其中 n 是字符串s的长度。
空间复杂度:O(n))
class Solution {
public:
void getNext (int* next, const string& s){
next[0] = -1;
int j = -1;
for(int i = 1;i < s.size(); i++){
while(j >= 0 && s[i] != s[j + 1]) {
j = next[j];
}
if(s[i] == s[j + 1]) {
j++;
}
next[i] = j;
}
}
bool repeatedSubstringPattern (string s) {
if (s.size() == 0) {
return false;
}
int next[s.size()];
getNext(next, s);
int len = s.size();
// 最长相等前后缀不包含的这个子串就是最小重复子串
// 如果len % (len - (next[len - 1] + 1)) == 0 ,则说明数组的长度正好可以被 (数组长度-最长相等前后缀的长度) 整除 ,说明该字符串有重复的子字符串。
if (next[len - 1] != -1 && len % (len - (next[len - 1] + 1)) == 0) {
return true;
}
return false;
}
};
七、代码随想录:双指针法
题目重复
八、代码随想录:栈与队列
232. 用栈实现队列(E)
力扣
F1 自写
一个栈实现,入栈时间复杂度O(1),出栈和peek时间复杂度都为O(n)
class MyQueue {
private:
stack<int> s;
public:
MyQueue() {
}
void push(int x) {
s.push(x);
}
int pop() {
stack<int> v;
while(!s.empty()) {
if(s.size() == 1) {
int tmp = s.top();
s.pop();
while(!v.empty()) {
s.push(v.top());
v.pop();
}
return tmp;
}
v.push(s.top());
s.pop();
}
return NULL;
}
int peek() {
stack<int> v;
while(!s.empty()) {
if(s.size() == 1) {
int tmp = s.top();
while(!v.empty()) {
s.push(v.top());
v.pop();
}
return tmp;
}
v.push(s.top());
s.pop();
}
return NULL;
}
bool empty() {
return s.empty();
}
};
F2 随想录
两个栈实现,一个输入栈一个输出栈,和F1类似,不过更简洁,复用性更高
class MyQueue {
public:
stack<int> stIn;
stack<int> stOut;
/** Initialize your data structure here. */
MyQueue() {
}
/** Push element x to the back of queue. */
void push(int x) {
stIn.push(x);
}
/** Removes the element from in front of queue and returns that element. */
int pop() {
// 只有当stOut为空的时候,再从stIn里导入数据(导入stIn全部数据)
if (stOut.empty()) {
// 从stIn导入数据直到stIn为空
while(!stIn.empty()) {
stOut.push(stIn.top());
stIn.pop(); // 这里要注意,stack的pop仅删除栈顶元素,但不返回该元素值,因此这里需要先top后pop
}
}
int result = stOut.top();
stOut.pop();
return result;
}
/** Get the front element. */
int peek() {
int res = this->pop(); // 直接使用已有的pop函数
stOut.push(res); // 因为pop函数弹出了元素res,所以再添加回去
return res;
}
/** Returns whether the queue is empty. */
bool empty() {
return stIn.empty() && stOut.empty();
}
};
其他方法
比如两个栈实现,和F1类似,不过push时间复杂度O(n),pop和peek时间复杂度O(1)。在入栈时就实现栈顶到栈底的顺序和队列一样
225. 用队列实现栈(E)
力扣
F1 双队列实现
pop时按顺序从一个队列中取出并放入另一个队列中,弹出最后一个,在复制到那个队列中
class MyStack {
public:
queue<int> que1;
queue<int> que2; // 辅助队列,用来备份
/** Initialize your data structure here. */
MyStack() {
}
/** Push element x onto stack. */
void push(int x) {
que1.push(x);
}
/** Removes the element on top of the stack and returns that element. */
int pop() {
int size = que1.size();
size--;
while (size--) { // 将que1 导入que2,但要留下最后一个元素
que2.push(que1.front());
que1.pop();
}
int result = que1.front(); // 留下的最后一个元素就是要返回的值
que1.pop();
que1 = que2; // 再将que2赋值给que1
while (!que2.empty()) { // 清空que2
que2.pop();
}
return result;
}
/** Get the top element. */
int top() {
return que1.back();
}
/** Returns whether the stack is empty. */
bool empty() {
return que1.empty();
}
};
F2 单队列实现
一个队列在模拟栈弹出元素的时候只要将队列头部的元素(除了最后一个元素外) 重新添加到队列尾部,此时在去弹出元素就是栈的顺序了
class MyStack {
public:
queue<int> que;
/** Initialize your data structure here. */
MyStack() {
}
/** Push element x onto stack. */
void push(int x) {
que.push(x);
}
/** Removes the element on top of the stack and returns that element. */
int pop() {
int size = que.size();
size--;
while (size--) { // 将队列头部的元素(除了最后一个元素外) 重新添加到队列尾部
que.push(que.front());
que.pop();
}
int result = que.front(); // 此时弹出的元素顺序就是栈的顺序了
que.pop();
return result;
}
/** Get the top element. */
int top() {
return que.back();
}
/** Returns whether the stack is empty. */
bool empty() {
return que.empty();
}
};
20. 有效的括号
力扣
F1 自写
class Solution {
public:
bool isValid(string s) {
// 思路:左括号入栈,若是右括号就出栈
stack<char> m;
unordered_map<char, char> tb = {
{'(', ')'},
{'{', '}'},
{'[', ']'}
};
for (auto i : s) {
m.push(i);
if (i == ')' || i == ']' || i == '}') {
m.pop();
if (m.empty() || i != (*tb.find(m.top())).second)
return false;
m.pop();
}
}
return m.empty();
}
};
F2 随想录版
class Solution {
public:
bool isValid(string s) {
// 如果s的长度为奇数,一定不符合要求
if (s.size() % 2 != 0) return false;
stack<char> m;
for (auto i : s) {
// 如果是左括号
if (i == '(') m.push(')');
else if (i == '[') m.push(']');
else if (i == '{') m.push('}');
// 如果是右括号
// 不匹配或空了
else if (m.empty() || m.top() != i) return false;
// 匹配
else m.pop();
}
return m.empty();
}
};
1047. 删除字符串中的所有相邻重复项
力扣
F1 自写
class Solution {
public:
string removeDuplicates(string s) {
// 入栈之前比一下,相同就pop,不同就push
stack<char> st;
for (auto i : s) {
if (st.empty() || st.top() != i) st.push(i);
else st.pop();
}
string a(st.size(),' ');
for (int i = st.size() - 1; i >= 0; i--) {
a[i] = st.top();
st.pop();
}
return a;
}
};
F2 随想录版
就需要翻转一下
class Solution {
public:
string removeDuplicates(string S) {
stack<char> st;
for (char s : S) {
if (st.empty() || s != st.top()) {
st.push(s);
} else {
st.pop(); // s 与 st.top()相等的情况
}
}
string result = "";
while (!st.empty()) { // 将栈中元素放到result字符串汇总
result += st.top();
st.pop();
}
reverse (result.begin(), result.end()); // 此时字符串需要反转一下
return result;
}
};
F3 将字符串直接作为栈
class Solution {
public:
string removeDuplicates(string s) {
string st;
for (auto i : s) {
if (st.empty() || st.back() != i) st.push_back(i);
else st.pop_back();
}
return st;
}
};
150. 逆波兰表达式求值
力扣
F1 栈
注意,-128*-128*-128*-128=2^ 31,这个数大于int最大范围2^31-1。最后乘以-1后的值是合法的,但是倒数第二步的值是非法的,所以中间计算过程要改为long,最后在转为int。
在C ++ 11中添加了stoi()函数将字符数组或字符串文字作为参数并返回其值
class Solution {
public:
int evalRPN(vector<string>& tokens) {
stack<int> st;
for (int i = 0; i < tokens.size(); i++) {
if (tokens[i] == "+" || tokens[i] == "-" || tokens[i] == "*" || tokens[i] == "/") {
int num1 = st.top();
st.pop();
int num2 = st.top();
st.pop();
if (tokens[i] == "+") st.push(num2 + num1);
if (tokens[i] == "-") st.push(num2 - num1);
if (tokens[i] == "*") st.push(num2 * (long)num1);
if (tokens[i] == "/") st.push(num2 / num1);
} else {
st.push(stoi(tokens[i]));
}
}
int result = st.top();
st.pop(); // 把栈里最后一个元素弹出(其实不弹出也没事)
return result;
}
};
239. 滑动窗口最大值
力扣
F1 自写,超时
虽然通过一些操作节省了时间,但最差的时间复杂度还是O((n-k+1)k)=O(nk)
class Solution {
public:
vector<int> maxSlidingWindow(vector<int>& nums, int k) {
// 每滑动一次,就入栈、对比。这里将vector视为stack
// 除非最大值是窗口的第一个位置,否则只需要和此窗口的最后一个比较即可
vector<int> st;
int tag = 0;
for (int i = 0; i < nums.size() - k + 1; i++) {
if (tag == 1) {
if (st.back() > nums[i+k-1]) {
st.push_back(st.back());
tag = 0;
continue;
}
else {
st.push_back(nums[i+k-1]);
tag = 1;
continue;
}
}
st.push_back(nums[i]);
int j = k-1;
while (j--) {
if (nums[i+j+1] > st.back()) {
st.pop_back();
st.push_back(nums[i+j+1]);
// 表示最大值的位置不是窗口的第一个
tag = 1;
}
else {
tag = 0;
}
}
}
return st;
}
};
F2 优先队列
class Solution {
public:
vector<int> maxSlidingWindow(vector<int>& nums, int k) {
int n = nums.size();
priority_queue<pair<int, int>> q;
for (int i = 0; i < k; ++i) {
q.emplace(nums[i], i);
}
vector<int> ans = {q.top().first};
for (int i = k; i < n; ++i) {
q.emplace(nums[i], i);
while (q.top().second <= i - k) {
q.pop();
}
ans.push_back(q.top().first);
}
return ans;
}
};
F3 单调队列
class Solution {
public:
vector<int> maxSlidingWindow(vector<int>& nums, int k) {
int n = nums.size();
deque<int> q;
// 先在前k个中取得初始值
for (int i = 0; i < k; ++i) {
while (!q.empty() && nums[i] >= nums[q.back()]) {
q.pop_back();
}
q.push_back(i);
}
vector<int> ans = {nums[q.front()]};
for (int i = k; i < n; ++i) {
while (!q.empty() && nums[i] >= nums[q.back()]) {
q.pop_back();
}
q.push_back(i);
while (q.front() <= i - k) {
q.pop_front();
}
ans.push_back(nums[q.front()]);
}
return ans;
}
};
随想录版
时间复杂度:使用单调队列的时间复杂度是 O(n)。虽然在队列中 push元素的过程中,还有pop操作呢,感觉不是纯粹的O(n)。但单调队列的实现中,nums 中的每个元素最多也就被 push_back 和 pop_back 各一次,没有任何多余操作,所以整体的复杂度还是 O(n)。
空间复杂度:因为我们定义一个辅助队列,所以是O(k)。
class Solution {
private:
class MyQueue { //单调队列(从大到小)
public:
deque<int> que; // 使用deque来实现单调队列
// 每次弹出的时候,比较当前要弹出的数值是否等于队列出口元素的数值,如果相等则弹出。同时pop之前判断队列当前是否为空。
// 这里就是滑动窗口移除最前面元素,如果那个元素刚好是nums[i-k],则说明最大的是滑动窗口前面的那个,在这轮里就要pop
void pop(int value) {
if (!que.empty() && value == que.front()) {
que.pop_front();
}
}
// 如果push的数值大于入口元素的数值,那么就将队列后端的数值弹出,直到push的数值小于等于队列入口元素的数值为止。
// 这样就保持了队列里的数值是单调从大到小的了。
void push(int value) {
while (!que.empty() && value > que.back()) {
que.pop_back();
}
que.push_back(value);
}
// 查询当前队列里的最大值 直接返回队列前端也就是front就可以了。
int front() {
return que.front();
}
};
public:
vector<int> maxSlidingWindow(vector<int>& nums, int k) {
MyQueue que;
vector<int> result;
for (int i = 0; i < k; i++) { // 先将前k的元素放进队列
que.push(nums[i]);
}
result.push_back(que.front()); // result 记录前k的元素的最大值
for (int i = k; i < nums.size(); i++) {
que.pop(nums[i - k]); // 滑动窗口移除最前面元素
que.push(nums[i]); // 滑动窗口前加入最后面的元素
result.push_back(que.front()); // 记录对应的最大值
}
return result;
}
};
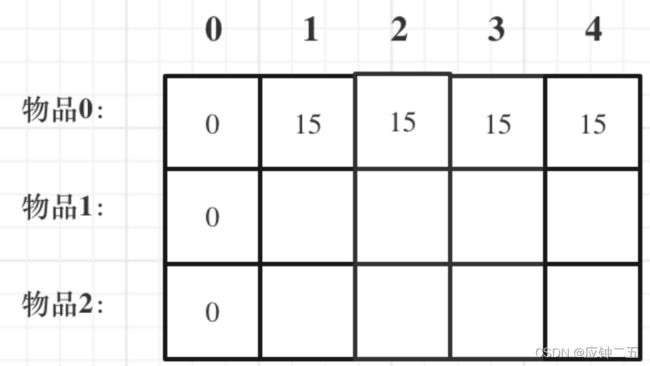
347. 前 K 个高频元素
力扣
F1 自写
O(logm)*O(m),最差为O(nlogn),不大好
class Solution {
public:
vector<int> topKFrequent(vector<int>& nums, int k) {
vector<int> v; // 保存结果
unordered_map<int, int> m; // 减去重复
priority_queue<pair<int, int>> q; // 对value即个数排序
// O(1)*O(n)
for (int i = 0; i < nums.size(); i++) {
m[nums[i]]++;
}
// 最简单的做法就是给出现次数数组排序,但时间复杂度:
// O(logm)*O(m),最差为O(nlogn)
for (auto it = m.begin(); it != m.end(); it++) {
q.emplace(it->second,it->first);
}
// O(k)
for(int i = 0; i < k; i++) {
v.push_back(q.top().second);
q.pop();
}
return v;
}
};
F2 随想录,优先级队列
空间复杂度:O(N)+O(k)=O(N)
class Solution {
public:
// 注意这里>是小顶堆,从小到大,和快排算法那些是反着的
class mycomparison {
public:
bool operator()(const pair<int, int>& lhs, const pair<int, int>& rhs) {
return lhs.second > rhs.second;
}
};
vector<int> topKFrequent(vector<int>& nums, int k) {
unordered_map<int, int> m; // 减去重复
// O(1)*O(n)
for (int i = 0; i < nums.size(); i++) {
m[nums[i]]++;
}
// 小顶堆,从小到大,堆顶是最小值
// 因为要统计最大前k个元素,只有小顶堆每次将最小的元素弹出,最后小顶堆里积累的才是前k个最大元素
// priority_queue的长度为k,因此每次插入的时间复杂度为O(logk),总为O(Nlogk)
// priority_queueF3 快速排序(待补充
时间复杂度O(N^2),平均情况下为O(n)
空间复杂度O(N)
九、代码随想录:二叉树
94.144.145.二叉树的前中后序遍历
F1 递归
前
class Solution {
public:
void traversal(TreeNode* cur, vector<int>& vec) {
if (cur == NULL) return;
vec.push_back(cur->val); // 中
traversal(cur->left, vec); // 左
traversal(cur->right, vec); // 右
}
vector<int> preorderTraversal(TreeNode* root) {
vector<int> result;
traversal(root, result);
return result;
}
};
中
void traversal(TreeNode* cur, vector<int>& vec) {
if (cur == NULL) return;
traversal(cur->left, vec); // 左
vec.push_back(cur->val); // 中
traversal(cur->right, vec); // 右
}
后
void traversal(TreeNode* cur, vector<int>& vec) {
if (cur == NULL) return;
traversal(cur->left, vec); // 左
traversal(cur->right, vec); // 右
vec.push_back(cur->val); // 中
}
F2 迭代
前
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<int> preorderTraversal(TreeNode* root) {
vector<int> result;
stack<TreeNode*> st;
if (root == NULL) return result;
st.push(root);
while (!st.empty()) {
TreeNode* node = st.top();
st.pop();
result.push_back(node->val);
if (node->right) st.push(node->right);
if (node->left) st.push(node->left);
}
return result;
}
};
中
和 前 的实现不一样
要先遍历到最左边,再开始入栈
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<int> inorderTraversal(TreeNode* root) {
vector<int> result;
stack<TreeNode*> st;
TreeNode* cur = root;
while (cur != NULL || !st.empty()) {
if (cur != NULL) { // 指针来访问节点,访问到最底层
st.push(cur); // 将访问的节点放进栈
cur = cur->left; // 左
} else {
cur = st.top(); // 从栈里弹出的数据,就是要处理的数据(放进result数组里的数据)
st.pop();
result.push_back(cur->val); // 中
cur = cur->right; // 右
}
}
return result;
}
};
后
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
// 前序遍历为中左右,改下顺序就为中右左,逆序就为左右中的后序遍历
vector<int> postorderTraversal(TreeNode* root) {
vector<int> result;
stack<TreeNode*> st;
if (root == NULL) return result;
st.push(root);
while (!st.empty()) {
TreeNode* node = st.top();
st.pop();
result.push_back(node->val);
if (node->left) st.push(node->left); // 相对于前序遍历,这更改一下入栈顺序 (空节点不入栈)
if (node->right) st.push(node->right); // 空节点不入栈
}
reverse(result.begin(), result.end());
return result;
}
};
F3 统一迭代法
不是很好理解
中
class Solution {
public:
vector<int> inorderTraversal(TreeNode* root) {
vector<int> result;
stack<TreeNode*> st;
if (root != NULL) st.push(root);
while (!st.empty()) {
TreeNode* node = st.top();
if (node != NULL) {
st.pop(); // 将该节点弹出,避免重复操作,下面再将右中左节点添加到栈中
if (node->right) st.push(node->right); // 添加右节点(空节点不入栈)
st.push(node); // 添加中节点
st.push(NULL); // 中节点访问过,但是还没有处理,加入空节点做为标记。
if (node->left) st.push(node->left); // 添加左节点(空节点不入栈)
} else { // 只有遇到空节点的时候,才将下一个节点放进结果集
st.pop(); // 将空节点弹出
node = st.top(); // 重新取出栈中元素
st.pop();
result.push_back(node->val); // 加入到结果集
}
}
return result;
}
};
前
class Solution {
public:
vector<int> preorderTraversal(TreeNode* root) {
vector<int> result;
stack<TreeNode*> st;
if (root != NULL) st.push(root);
while (!st.empty()) {
TreeNode* node = st.top();
if (node != NULL) {
st.pop();
if (node->right) st.push(node->right); // 右
if (node->left) st.push(node->left); // 左
st.push(node); // 中
st.push(NULL);
} else {
st.pop();
node = st.top();
st.pop();
result.push_back(node->val);
}
}
return result;
}
};
后
class Solution {
public:
vector<int> postorderTraversal(TreeNode* root) {
vector<int> result;
stack<TreeNode*> st;
if (root != NULL) st.push(root);
while (!st.empty()) {
TreeNode* node = st.top();
if (node != NULL) {
st.pop();
st.push(node); // 中
st.push(NULL);
if (node->right) st.push(node->right); // 右
if (node->left) st.push(node->left); // 左
} else {
st.pop();
node = st.top();
st.pop();
result.push_back(node->val);
}
}
return result;
}
};
十、代码随想录:回溯算法
力扣
F1
力扣
F1
十一、代码随想录:贪心算法
力扣
F1
力扣
F1
十二、代码随想录:动态规划
509、斐波那契数(E)
F1 暴力递归
class Solution {
public:
int fib(int n) {
if(n<2) return n;
return fib(n-1)+fib(n-2);
}
};
执行用时:12 ms,
时间复杂度O(2^n),空间复杂度O(n)
问题:重叠子问题,有重复计算,时间复杂度高
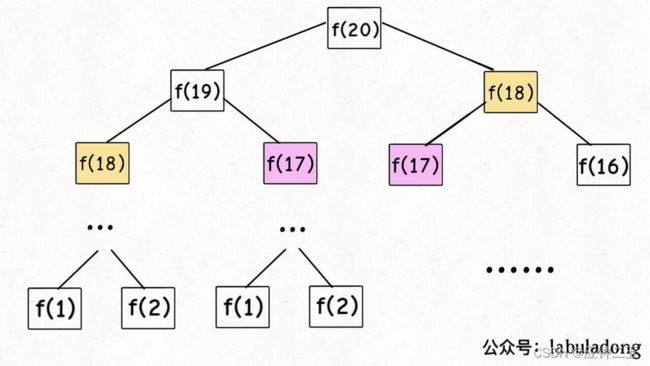

F2 动态规划dp
代码随想录标准解法
class Solution {
public:
int fib(int n) {
if(n<2) return n;// 注意要先返回特殊值,否则vector创建dp并赋初值的过程会报错
vector<int> dp(n+1,0);
dp[1]=1;
for(int i=2;i<=n;i++){
dp[i]=dp[i-1]+dp[i-2];
}
return dp[n];
}
};
时间复杂度和空间复杂度都为O(N)
执行用时:0 ms
F3 精简
// 自写
class Solution {
public:
int fib(int n) {
if(n<2) return n;
int pre1=0;int pre2=1;int curr;
for(int i=2;i<=n;i++){
curr=pre1+pre2;
pre1=pre2;
pre2=curr;
}
return curr;
}
};
// 代码随想录版本,用的数组
class Solution {
public:
int fib(int N) {
if (N <= 1) return N;
int dp[2];
dp[0] = 0;
dp[1] = 1;
for (int i = 2; i <= N; i++) {
int sum = dp[0] + dp[1];
dp[0] = dp[1];
dp[1] = sum;
}
return dp[1];
}
};
时间复杂度O(n),空间复杂度O(1)
70、爬楼梯(E)
F1、动态规划
class Solution {
public:
int climbStairs(int n) {
if(n<=2) return n;
vector<int> dp(n+1,1);//可以省略dp[0] = 1;dp[1] = 1;的初始化
for(int i=2;i<=n;i++){
dp[i]=dp[i-1]+dp[i-2];
}
return dp[n];
}
};
随想录这个代码的好处就是,避免了对dp[0]这个没有意义的东西赋值
// 随想录
class Solution {
public:
int climbStairs(int n) {
if (n <= 1) return n; // 因为下面直接对dp[2]操作了,防止空指针
vector<int> dp(n + 1);
dp[1] = 1;
dp[2] = 2;
for (int i = 3; i <= n; i++) { // 注意i是从3开始的
dp[i] = dp[i - 1] + dp[i - 2];
}
return dp[n];
}
};
F2、空间上进行压缩
使得原来的 On空间复杂度优化为 O1 复杂度
class Solution {
public:
int climbStairs(int n) {
if(n<=2) return n;
int pred=1;
int curr=1;
for(int i=2;i<=n;i++){
int mm=pred+curr;
curr=pred;
pred=mm;
}
return pred;
}
};
执行用时:0 ms,
内存消耗:5.8 MB
官方代码
class Solution {
public:
int climbStairs(int n) {
int p = 0, q = 0, r = 1;
for (int i = 1; i <= n; i++) {
p = q;
q = r;
r = p + q;
}
return r;
}
};
扩展
这道题目还可以继续深化,就是一步一个台阶,两个台阶,三个台阶,直到m个台阶,有多少种方法爬到n阶楼顶。
这又有难度了,这其实是一个完全背包问题,但力扣上没有这种题目,所以后续我在讲解背包问题的时候,今天这道题还会拿从背包问题的角度上来再讲一遍。
自写
问题:没有i-j>=0的判断
#include 随想录代码
class Solution {
public:
int climbStairs(int n) {
vector<int> dp(n + 1, 0);
dp[0] = 1;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) { // 把m换成2,就可以AC爬楼梯这道题
if (i - j >= 0) dp[i] += dp[i - j];
}
}
return dp[n];
}
};
746. 使用最小花费爬楼梯(E)
F1 自写
定义dp[i]为:第一步是不花费体力,最后一步是花费体力的。
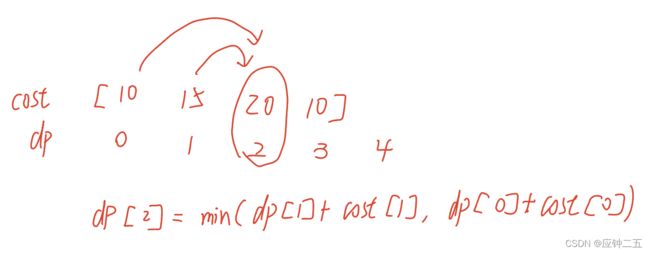
class Solution {
public:
int minCostClimbingStairs(vector<int>& cost) {
int m=cost.size();
vector<int> dp(m+1,0);
for(int i=2;i<=m;i++){
dp[i]=min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]);
}
return dp[m];
}
};
随想录版本,没啥差别
class Solution {
public:
int minCostClimbingStairs(vector<int>& cost) {
vector<int> dp(cost.size() + 1);
dp[0] = 0; // 默认第一步都是不花费体力的
dp[1] = 0;
for (int i = 2; i <= cost.size(); i++) {
dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);
}
return dp[cost.size()];
}
};
空间压缩
class Solution {
public:
int minCostClimbingStairs(vector<int>& cost) {
int m=cost.size();
int curr=0,pre1=0,pre2=0;
for(int i=2;i<=m;i++){
curr=min(pre2+cost[i-1],pre1+cost[i-2]);
pre1=pre2;
pre2=curr;
}
return curr;
}
};
F2 随想录
这里的dp[i],指爬过这个楼梯的,故如dp[3]=min(dp[2]+dp[1])+cost[3],即到这层楼梯的最小dp加爬过这一层的体力耗费。然后最后返回前两个dp中最小的那个就行
定义的dp[i]意思是是第一步是要花费体力的,最后一步不用花费体力了,因为已经支付了。
class Solution {
public:
int minCostClimbingStairs(vector<int>& cost) {
vector<int> dp(cost.size());
dp[0] = cost[0];
dp[1] = cost[1];
for (int i = 2; i < cost.size(); i++) {
dp[i] = min(dp[i - 1], dp[i - 2]) + cost[i];
}
// 注意最后一步可以理解为不用花费,所以取倒数第一步,第二步的最少值
return min(dp[cost.size() - 1], dp[cost.size() - 2]);
}
};
空间压缩
class Solution {
public:
int minCostClimbingStairs(vector<int>& cost) {
int dp0 = cost[0];
int dp1 = cost[1];
for (int i = 2; i < cost.size(); i++) {
int dpi = min(dp0, dp1) + cost[i];
dp0 = dp1; // 记录一下前两位
dp1 = dpi;
}
return min(dp0, dp1);
}
};
62.不同路径(M)
F1 动态规划
自写
class Solution {
public:
int uniquePaths(int m, int n) {
vector<vector<int>> dp(m,vector<int>(n,0));
for(int i=0;i<m;i++){
for(int j=0;j<n;j++){
if(i==0&&j==0) dp[i][j]=1;
else if(i==0) dp[i][j]=dp[i][j-1];
else if(j==0) dp[i][j]=dp[i-1][j];
else dp[i][j]=dp[i][j-1]+dp[i-1][j];
}
}
return dp[m-1][n-1];
}
};
随想录,区别就是这里先初始化i=0和j=0的地方,再计算中间部分的
class Solution {
public:
int uniquePaths(int m, int n) {
vector<vector<int>> dp(m, vector<int>(n, 0));
for (int i = 0; i < m; i++) dp[i][0] = 1;
for (int j = 0; j < n; j++) dp[0][j] = 1;
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
}
return dp[m - 1][n - 1];
}
};
时间复杂度O(m *n),空间复杂度O(m *n)
一维数组空间压缩,滚动数组
class Solution {
public:
int uniquePaths(int m, int n) {
vector<int> dp(n,1);
for(int i=1;i<m;i++){
for(int j=1;j<n;j++){
dp[j]=dp[j]+dp[j-1];
}
}
return dp[n-1];
}
};
时间复杂度O(m *n),空间复杂度O(n)
F2 深度搜索,待补充
随想录
但这个方法会超时
F3 数论方法
 在这m + n - 2 步中,一定有 m - 1 步是要向下走的,不用管什么时候向下走。
在这m + n - 2 步中,一定有 m - 1 步是要向下走的,不用管什么时候向下走。
那么有几种走法呢? 可以转化为,给你m + n - 2个不同的数,随便取m - 1个数,有几种取法。
那么这就是一个组合问题了。

class Solution {
public:
int uniquePaths(int m, int n) {
long long ans = 1;
for (int x = n, y = 1; y < m; ++x, ++y) {
ans = ans * x / y;
}
return ans;
}
};
时间复杂度:O(m),空间复杂度:O(1)
63.不同路径II(M)
F1 自写
在原来基础上修改,加入起点和终点有障碍物的判定,初始化方面第一行和第一列,一旦出现一个障碍物,后面的dp都会无通路。最后加入一个如果当前位置是障碍物,dp置零
class Solution {
public:
int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
int m=obstacleGrid.size();
int n=obstacleGrid[0].size();
vector<vector<int>> dp(m, vector<int>(n, 0));
// 因为这个i=0和j=0行赋初始值写的不好,因此多了下面两行额外的赋值
if(obstacleGrid[0][0]==1||obstacleGrid[m-1][n-1]==1) return 0;
dp[0][0]=1;
for (int i = 1; i < m; i++){
if(obstacleGrid[i][0]==0&&dp[i-1][0]!=0) dp[i][0] = 1;
}
//赋值操作可以改成for (int i = 0; i < m && obstacleGrid[i][0] == 0; i++) dp[i][0] = 1;
//注意代码里for循环的终止条件,一旦遇到obstacleGrid[i][0] == 1的情况就停止dp[i][0]的赋值1的操作,dp[0][j]同理
for (int j = 1; j < n; j++){
if(obstacleGrid[0][j]==0&&dp[0][j-1]!=0) dp[0][j] = 1;;
}
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
if(obstacleGrid[i][j]==1) dp[i][j]=0;
}
}
return dp[m - 1][n - 1];
}
};
F2 随想录简化版
class Solution {
public:
int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
int m = obstacleGrid.size();
int n = obstacleGrid[0].size();
vector<vector<int>> dp(m, vector<int>(n, 0));
// 注意代码里for循环的终止条件,一旦遇到obstacleGrid[i][0] == 1的情况就停止dp[i][0]的赋值1的操作,dp[0][j]同理
for (int i = 0; i < m && obstacleGrid[i][0] == 0; i++) dp[i][0] = 1;
for (int j = 0; j < n && obstacleGrid[0][j] == 0; j++) dp[0][j] = 1;
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
// 递推公式只要考虑一下障碍,就不赋值了就可以了
if (obstacleGrid[i][j] == 1) continue;
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
}
return dp[m - 1][n - 1];
}
};
343.整数拆分(M) (再看一遍)
F1 数学方法
可以发现,10->3^ 2+4 11->3^3+2 12->3 ^4,即最大值都3的几次方,若有余的话,大于1则直接乘,小于1则加上3
class Solution {
public:
int integerBreak(int n) {
if(n<2) return 0;
if(n<=3) return n-1;
int a;
if(n%3>1) return pow(3,n/3)*(n%3);
else return pow(3,n/3-1)*(n%3+3);
}
};
时间复杂度和空间复杂度都为O(1)
F2 动态规划
dp[i]的意义是分拆数字i,可以得到的最大乘积为dp[i]。
dp[0] = 1,dp[1] = 1的初始化比较牵强,无法解释,因此来避免,从dp[2]开始
思路是max((i - j) * j, dp[i - j] * j),再与dp[i]比较,因为是在不断递归
也可以这么理解,j * (i - j) 是单纯的把整数拆分为两个数相乘,而j * dp[i - j]是拆分成两个以及两个以上的个数相乘。
class Solution {
public:
int integerBreak(int n) {
vector<int> dp(n + 1);
dp[2] = 1;
for (int i = 3; i <= n ; i++) {
for (int j = 1; j < i - 1; j++) {
dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j));
}
}
return dp[n];
}
};
时间复杂度:O(n^2) 空间复杂度:O(n)
F3 贪心算法
class Solution {
public:
int integerBreak(int n) {
if (n == 2) return 1;
if (n == 3) return 2;
if (n == 4) return 4;
int result = 1;
while (n > 4) {
result *= 3;
n -= 3;
}
result *= n;
return result;
}
};
时间复杂度:O(n) 空间复杂度:O(1)
96.不同的二叉搜索树(M)(再看一遍)
- 若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值;
- 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值;
- 它的左、右子树也分别为二叉搜索树
F1 动态规划
dp[i] += dp[以j为头结点左子树节点数量] * dp[以j为头结点右子树节点数量]
class Solution {
public:
int numTrees(int n) {
// dp[i] : 1到i为节点组成的二叉搜索树的个数为dp[i]
// dp[i] += dp[以j为头结点左子树节点数量] * dp[以j为头结点右子树节点数量]
vector<int> dp(n+1);
dp[0]=1; // 空节点也是一棵二叉树,也是一棵二叉搜索树
for(int i=1;i<=n;i++){
for(int j=1;j<=i;j++){
dp[i] += dp[j-1]*dp[i-j];
}
}
return dp[n];
}
};
时间复杂度 : O(n^2) 空间复杂度:O(n)
F2 数学(未看)
class Solution {
public:
int numTrees(int n) {
long long C = 1;
for (int i = 0; i < n; ++i) {
C = C * 2 * (2 * i + 1) / (i + 2);
}
return (int)C;
}
};
时间复杂度 : O(n) 空间复杂度:O(1)
01背包:
二维dp数组

dp[i][j] 表示从下标为[0-i]的物品里任意取,放进容量为j的背包,价值总和最大是dp[i][j] 。
dp[i][j] 由两部分构成:
- 不放物品i:即背包已经满了,没容量了。因此dp[i][j]=dp[i-1][j],等于没放前的dp
- 放物品i:dp[i][j]=dp[i-1][j-weight[i]]+value[i]
因此递归公式为两个取max
void test_2_wei_bag_problem1() {
vector<int> weight = {1, 3, 4};
vector<int> value = {15, 20, 30};
int bagweight = 4;
// 二维数组
vector<vector<int>> dp(weight.size(), vector<int>(bagweight + 1, 0));
// 初始化
for (int j = weight[0]; j <= bagweight; j++) {
dp[0][j] = value[0];
}
// weight数组的大小 就是物品个数
for(int i = 1; i < weight.size(); i++) { // 遍历物品
for(int j = 0; j <= bagweight; j++) { // 遍历背包容量
if (j < weight[i]) dp[i][j] = dp[i - 1][j];
else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
}
}
cout << dp[weight.size() - 1][bagweight] << endl;
}
int main() {
test_2_wei_bag_problem1();
}
一维dp数组(更常用)
简化为一维
在一维dp数组中,dp[j]表示:容量为j的背包,所背的物品价值可以最大为dp[j]。
注意这里遍历背包是倒序,来保证物品i只被放入一次

void test_1_wei_bag_problem() {
vector<int> weight = {1, 3, 4};
vector<int> value = {15, 20, 30};
int bagWeight = 4;
// 初始化
vector<int> dp(bagWeight + 1, 0);
for(int i = 0; i < weight.size(); i++) { // 遍历物品
for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
}
}
cout << dp[bagWeight] << endl;
}
int main() {
test_1_wei_bag_problem();
}
416.分割等和子集(M)
F1 自写
直接01背包改的,这里只需要判断最后的dp是否为sum/2即可,因为这里的容量是sum/2,因此只要凑齐一个,说明另一个一定也是sum/2
注意这里sum应该为偶数才能分割。
踩坑:不能判断sum/2,因为int会丢掉小数;也不能float a=sum/2,因为sum是int,除一个数后还是int
class Solution {
public:
bool canPartition(vector<int>& nums) {
int sum=accumulate(nums.begin(),nums.end(),0);
// sum应该是偶数才能分割
if(sum%2==1) return false;
vector<int> dp(sum/2 + 1, 0);
for(int i = 0; i < nums.size(); i++) { // 遍历物品
for(int j = sum/2; j >= nums[i]; j--) { // 遍历背包容量
dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]);
}
}
// 这里只需要判断最后的dp是否为sum/2即可,因为这里的容量是sum/2,因此只要凑齐一个,说明另一个一定也是sum/2
if(dp[sum/2]==sum/2) return true;
else return false;
}
};
时间复杂度O(n^2) 空间复杂度O(n)
F2 随想录
通过累加和计算sum,避免了使用accumulate这个算法
class Solution {
public:
bool canPartition(vector<int>& nums) {
int sum = 0;
// dp[i]中的i表示背包内总和
// 题目中说:每个数组中的元素不会超过 100,数组的大小不会超过 200
// 总和不会大于20000,背包最大只需要其中一半,所以10001大小就可以了
vector<int> dp(10001, 0);
for (int i = 0; i < nums.size(); i++) {
sum += nums[i];
}
if (sum % 2 == 1) return false;
int target = sum / 2;
// 开始 01背包
for(int i = 0; i < nums.size(); i++) {
for(int j = target; j >= nums[i]; j--) { // 每一个元素一定是不可重复放入,所以从大到小遍历
dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]);
}
}
// 集合中的元素正好可以凑成总和target
if (dp[target] == target) return true;
return false;
}
};
1049. 最后一块石头的重量 II(M)
F1 自写动态规划
class Solution {
public:
int lastStoneWeightII(vector<int>& stones) {
int sum=accumulate(stones.begin(),stones.end(),0);
vector<int> dp(sum/2 + 1, 0);
for(int i = 0; i < stones.size(); i++) { // 遍历物品
for(int j = sum/2; j >= stones[i]; j--) { // 遍历背包容量
dp[j] = max(dp[j], dp[j - stones[i]] + stones[i]);
}
}
// dp用来计算最接近sum/2的累加和,则另一堆石头为sum-dp
return sum-dp[sum/2]*2;
}
};
时间复杂度:O(m × n), m是石头总重量(准确的说是总重量的一半),n为石头块数
空间复杂度:O(m)
随想录动态规划
class Solution {
public:
int lastStoneWeightII(vector<int>& stones) {
vector<int> dp(15001, 0);
int sum = 0;
for (int i = 0; i < stones.size(); i++) sum += stones[i];
int target = sum / 2;
for (int i = 0; i < stones.size(); i++) { // 遍历物品
for (int j = target; j >= stones[i]; j--) { // 遍历背包
dp[j] = max(dp[j], dp[j - stones[i]] + stones[i]);
}
}
return sum - dp[target] - dp[target];
}
};
494. 目标和(M)
F1 自写
将一个数组分为a、b两块,即a块里的元素均赋+,b赋-,则a-b=target,a+b=sum,可推出a=(sum+target)/2,即此问题转化为看数组中各个元素组合为a有多少种可能。
这里dp[j]表示装满j有dp种可能。而dp[j]=dp[j-nums[i]]的累加和,即

注意:
- 如果sum与target的和为奇数的话,如sum奇target偶,则怎么加符号都构不成target
- 用abs[target]
class Solution {
public:
int findTargetSumWays(vector<int>& nums, int target) {
int sum=accumulate(nums.begin(),nums.end(),0);
// 如果sum与target的和为奇数的话,如sum奇target偶,则怎么加符号都构不成target
// 用abs[target]
if((sum+target)%2==1||abs(target)>sum) return 0;
int a=(sum+target)/2;
int n=nums.size();
vector<int> dp(a+1,0);
dp[0]=1;
for(int i=0;i<n;i++){ // 遍历物品
for(int j=a;j>=nums[i];j--){
dp[j]+=dp[j-nums[i]];
}
}
return dp[a];
}
};
时间复杂度:O(n × m),n为正数个数,m为背包容量
空间复杂度:O(m),m为背包容量
随想录
区别只是没用accumulate算法
int sum = 0;
for (int i = 0; i < nums.size(); i++) sum += nums[i];
F2 回溯算法(待补充)
回溯
474.一和零(M)
力扣
F1
注意,这里m即行序列,需要逆序,n的话无所谓
class Solution {
public:
int findMaxForm(vector<string>& strs, int m, int n) {
vector<vector<int>> dp(m+1,vector<int>(n+1,0));
// 这里可以简化为for (string str : strs)
for(int k=0;k<strs.size();k++){
int count1=0,count2=0;
for(auto ch:strs[k]){
if(ch=='0') count1++;
else count2++;
}
for(int i=m;i>=count1;i--){
for(int j=n;j>=count2;j--){
dp[i][j]=max(dp[i][j],dp[i-count1][j-count2]+1);
}
}
}
return dp[m][n];
}
};
198、打家劫舍/House Robber(E)
F1 笨蛋规划
最大值只可能在最后两个房子中间,即抢/不抢最后一个房子。
这个自己写的辣鸡方法,是想着每次的sum由自己和sum[n-2],sum[n-3]…sum[0]里最大的构成,就又创建了个set来自动排序,最后构成循环
但其实只需要构建一个最大值的数组dp,dp=max(前一个房子的dp,当前+前前个房子的dp)即可
class Solution {
public:
int rob(vector<int>& nums) {
int nn=nums.size();
vector<int> sum(nn,0);//这里nn+1使得sum从1开始
set<int> mm;
if(nn==1) return nums[0];
if(nn==2) return max(nums[0],nums[1]);
sum[0]=nums[0];
sum[1]=nums[1];
for(int i=2;i<nn;i++){
mm.insert(sum[i-2]);
sum[i]=nums[i]+*(--mm.end());
}
return max(sum[nn-1],sum[nn-2]);
}
};
4ms 7.8MB
F2 动态规划
class Solution {
public:
int rob(vector<int>& nums) {
// 这种判断要加,总是忘
if(nums.empty()) return 0;
int n=nums.size();
vector<int> dp(n+1,0);
dp[1]=nums[0];
for(int i=2;i<=n;i++){
dp[i]=max(dp[i-1],nums[i-1]+dp[i-2]);
}
return dp[n];
}
};
0ms 7.5MB
F3 精简
class Solution {
public:
int rob(vector<int>& nums) {
// 这种判断要加,总是忘
if(nums.empty()) return 0;
int n=nums.size();
if(n==1) return nums[0];
int cur,pre1=0,pre2=0;
for(int i=0;i<n;i++){
cur=max(pre1,nums[i]+pre2);
pre2=pre1;
pre1=cur;
}
return cur;
}
};
413、等差数列划分Arithmetic Slices(M)
F1 自己写的
class Solution {
public:
int numberOfArithmeticSlices(vector<int>& nums) {
int n=nums.size();
if(n<3) return 0;
int cha=nums[0]-nums[1],a=0,count=1;
for(int i=1;i<n-1;i++){
if(cha==nums[i]-nums[i+1]) count++;
else{
count=1;
cha=nums[i]-nums[i+1];
}
a+=count-1;// 这里count定义为两个数之间的间隔,比如三个数的等差,count为2。然后c为2,a+1,c变为3,a=3,在原来基础上加了c-1
}
return a;
}
};
执行用时 4ms
F2 标准
可以发现,子数组从3->1 4->3 5-> 6,是每多一个,dp+1,然后再累加和。只需要判断前两个和后两个的差是否相等。这里创建了n的数组,填充0,这样的话即使中间断掉,再有三个连续的满足条件的时候,也是从0开始累加。
class Solution {
public:
int numberOfArithmeticSlices(vector<int>& nums) {
int n=nums.size();
if(n<3) return 0;
vector<int> dp(n,0);
for(int i=2;i<n;i++){
if(nums[i]-nums[i-1]==nums[i-1]-nums[i-2]){
dp[i]=dp[i-1]+1;
}
}
return accumulate(dp.begin(),dp.end(),0);
}
};
基本动态规划:二维
64、最小路径和/Minimum Path Sum(M)
F1、扩充dp并填最大值
class Solution {
public:
int minPathSum(vector<vector<int>>& grid) {
int h=grid.size();
int w=grid[0].size();
// 这里如果要用vector进行二维赋值:vector> dp(m, vector(n, 0));
int dp[h+1][w+1];
memset(dp,0x3f,sizeof(dp));
/*memset(起始地址,赋的值,大小),这里默认用0x3f表示赋最大
0x3f=0011;C++中int型变量所占的位数为4个字节,即32位,因为4个字节均为0x3f时,0x3f3f3f3f的十进制是1061109567,也就是10^ 9级别的(和0x7fffffff一个数量级),而一般场合下的数据都是小于10^9的,所以它可以作为无穷大使用而不致出现数据大于无穷大的情形。并且可以保证无穷大加无穷大仍然不会超限*/
for(int i=0;i<h;i++){
for(int j=0;j<w;j++){
dp[i+1][j+1]=grid[i][j]+min(dp[i][j+1],dp[i+1][j]);
if(i==0&&j==0) dp[i+1][j+1]=grid[0][0];
}
}
return dp[h][w];
}
};
4-8ms波动,9.5MB
F2、不扩充,靠if增加条件
F3、再进行空间压缩到一维,自己写的压缩,实际并没有压缩,只是维度变了…
class Solution {
public:
int minPathSum(vector<vector<int>>& grid) {
int h=grid.size();
int w=grid[0].size();
// 这里如果要用vector进行二维赋值:vector> dp(m, vector(n, 0));
int dp[h*w];
memset(dp,0,sizeof(dp));
for(int i=0;i<h;i++){
for(int j=0;j<w;j++){
if(i==0&&j==0) dp[i]=grid[i][j];
else if(i==0) dp[i*w+j]=grid[i][j]+dp[i*w+j-1];
else if(j==0) dp[i*w]=grid[i][j]+dp[(i-1)*w];
else dp[i*w+j]=grid[i][j]+min(dp[(i-1)*w+j],dp[i*w+j-1]);
}
}
return dp[h*w-1];
}
};
F4、真正的空间压缩
因为 dp 矩阵的每一个值只和左边和上面的值相关,我们可以使用空间压缩将 dp 数组压缩为
一维。对于第 i 行,在遍历到第 j 列的时候,因为第 j-1 列已经更新过了,所以 dp[j-1] 代表 dp[i][j-1]
的值;而 dp[j] 待更新,当前存储的值是在第 i-1 行的时候计算的,所以代表 dp[i-1][j] 的值。
class Solution {
public:
int minPathSum(vector<vector<int>>& grid) {
// dp一行一行的计算,size为列数,即w
// dp[j-1]代表刚更新的前面那个数,dp[j]里存的是上面那行更新的数,对应应计算值上面的那个
int h=grid.size(),w=grid[0].size();
vector<int> dp(w,0);
for(int i=0;i<h;i++){
for(int j=0;j<w;j++){
if(i==0&&j==0) dp[j]=grid[i][j];
else if(i==0) dp[j]=dp[j-1]+grid[i][j];
else if(j==0) dp[j]=dp[j]+grid[i][j];
else dp[j]=grid[i][j]+min(dp[j],dp[j-1]);
}
}
return dp[w-1];
}
};
542. 01矩阵/01 Matrix (M)
F1、自己写的错误解法
思路有问题,这里是判断如果Mat为0,存0,如果为1,存上下左右里dp最小的,周围有0就是0,周围有1就是1里面最小的。但是!!!!!!!第一次循环的时候后面和下面都是默认值啊md
class Solution {
public:
vector<vector<int>> updateMatrix(vector<vector<int>>& mat) {
// 填充一圈最大值,中间包围m,构成dp,最后输出中间的m
int h=mat.size(),w=mat[0].size();
vector<vector<int>> m(h, vector<int>(w, 0)); // 存放输出结果
int dp[h+2][w+2]; // 上下左右进行max的扩充
memset(dp,0x3f,sizeof(dp));
for(int i=0;i<h;i++){
for(int j=0;j<w;j++){
if(mat[i][j]==0) {dp[i+1][j+1]=0;m[i][j]=dp[i+1][j+1];}
else if(mat[i][j]==1){
dp[i+1][j+1]=min({dp[i+2][j+1],dp[i][j+1],dp[i+1][j+2],dp[i+1][j]})+1;
m[i][j]=dp[i+1][j+1];
}
}
}
return m;
}
};
F2、正确解法
填充的dp为最大值
第一轮左上到右下,取左和上和本身里的最小值;第二轮右下到左上,取下和右和本身里的最小值

class Solution {
public:
vector<vector<int>> updateMatrix(vector<vector<int>>& mat) {
// 这个为空的判定,老忘
if(matrix.empty()) return {};
int h=mat.size(),w=mat[0].size();
vector<vector<int>> m(h, vector<int>(w, INT_MAX-1)); // INT_MAX = 2^31-1
for(int i=0;i<h;i++){
for(int j=0;j<w;j++){
if(mat[i][j]==0) m[i][j]=0;
else{
if(j>0) m[i][j]=min(m[i][j],m[i][j-1]+1);//顺序是一行一行的,所以先判断j后判断i
if(i>0) m[i][j]=min(m[i][j],m[i-1][j]+1);
}
}
}
for(int i=h-1;i>=0;i--){
for(int j=w-1;j>=0;j--){
if(j<w-1) m[i][j]=min(m[i][j],m[i][j+1]+1);
if(i<h-1) m[i][j]=min(m[i][j],m[i+1][j]+1);
}
}
return m;
}
};
221、最大正方形/Maximal Square (Medium)
F1、自写
思路: 构建一个dp存储。
一直报解答错误,最后发现是因为*判断三个数都相等,不能用(dp[(i-1)n+j-1]==dp[in+j-1]==dp[(i-1)n+j])
class Solution {
public:
int maximalSquare(vector<vector<char>>& matrix) {
int m=matrix.size(),n=matrix[0].size();
vector<int> dp(m*n,0);
for(int i=0;i<m;i++){
for(int j=0;j<n;j++){
if(matrix[i][j]=='1'){
dp[i*n+j]=1;
if(i!=0&&j!=0){
if(dp[(i-1)*n+j-1]>=1&&dp[i*n+j-1]>=1&&dp[(i-1)*n+j]>=1){
if((dp[(i-1)*n+j-1]==dp[i*n+j-1])&&(dp[i*n+j-1]==dp[(i-1)*n+j])) dp[i*n+j]=dp[i*n+j-1]+1;
else dp[i*n+j]=min({dp[(i-1)*n+j-1],dp[i*n+j-1],dp[(i-1)*n+j]})+1;
//三个都相等,加一,不都相等取最大
}
}
}
}
}
sort(dp.begin(),dp.end());
return dp[m*n-1]*dp[m*n-1];
}
};
执行用时68ms
F2、答案解法
class Solution {
public:
int maximalSquare(vector<vector<char>>& matrix) {
// 老忘
if(matrix.empty()||matrix[0].empty()) return 0;
int m=matrix.size(),n=matrix[0].size();
int max_side=0;// 通过这个就可以直接得到最大值了,不用遍历也不用排序什么的
vector<vector<int>> dp(m+1,vector<int>(n+1,0));
for(int i=1;i<=m;i++){
for(int j=1;j<=n;j++){
if(matrix[i-1][j-1]=='1') dp[i][j]=min({dp[i-1][j-1],dp[i][j-1],dp[i-1][j]})+1;
max_side=max(max_side,dp[i][j]);
}
}
return max_side*max_side;
}
};
执行用时52ms
分割类型题
279、完全平方数/Perfect Squares (Medium)
F1 动态规划(看答案做的没想出来
class Solution {
public:
int numSquares(int n) {
// 这里542题中用了INT_MAX-1,而例中却用了INT_MAX
vector<int> dp(n+1,INT_MAX-1);
dp[0]=0;
for(int i=1;i<=n;i++){
for(int j=1;j*j<=i;j++){
// 此dp[i]可以取的最小值即为 1 + min(dp[i-1],dp[i-4],dp[i-9]...)
// 这里本来不理解这min有什么用处,毕竟前一项dp[i]被初始化为最大
// 这里在j的循环中,只有j=1的循环中dp[i]是最大,之后就成了比较min(dp[i-1],dp[i-4],dp[i-9]...
dp[i]=min(dp[i],dp[i-j*j]+1);
}
}
return dp[n];
}
};
322、零钱兑换
F1、动态规划
class Solution {
public:
int coinChange(vector<int>& coins, int amount) {
vector<int> dp(amount+1,amount+2);//初始化vector为amount+1个amount+2
dp[0]=0;
for(int i=0;i<=amount;i++){
for(const int& coin : coins){
if(i>=coin){
dp[i]=std::min(dp[i],dp[i-coin]+1);
}
}
}
return dp[amount]==amount+2?-1:dp[amount];
}
};
80ms,14mb